债务结构、展期风险与创新型中小企业的融资难题
2022-04-20 08:44李文健徐朝阳
产经评论 2022年1期
翁 翕 李文健 徐朝阳
一 引言及文献述评
中小企业融资难是我国社会各界广泛且长期关注的问题。2010年12月，民建中央发布的专题报告《后危机时代中小企业转型与创新的调查与建议》显示，我国中小企业的平均寿命为3.7年，而无法获得长期稳定的融资是造成中小企业无以为继的主要原因之一。何志健(2018)指出“2016年底，在国内市场主体中占据超过 99%的中小企业从银行等相关机构中得到的贷款在所有贷款额度中占据的比重仅仅是20%……很少有中小企业能获得银行基准利率上浮10%，一些企业承担着基准利率上浮30%-50%的贷款成本。”吴晓波(2018)指出“在过去很多年里，存在两个‘60%’现象，即有60%的民营企业从来没有从银行贷到过款，而获得贷款服务的企业中，又有60%是一年期短贷。”可见企业的贷款，尤其是长期贷款需求普遍没有得到满足。
创新是经济增长的源泉，创新型企业是我国经济高质量发展的重要生力军。但由于抵押品不足和收益不确定性，新创立企业往往缺乏稳定的融资，而中小创新型企业融资难题尤其严重。这也是各国纷纷出台相关政策来为中小创新型企业提供长期贷款的原因(蓝寿荣和陈源，2008)。就我国而言，国务院批准设立了“科技型中小企业技术创新基金”，用于支持科技型中小企业技术创新。除此之外，国务院自2015年3月提出选择符合条件的银行业金融机构探索“投贷联动”。当前，我们关注和研究我国中小企业融资难的问题，在一定程度上可以说是为了研究如何给我国创新型企业的发展和崛起尽可能营造良好的外部环境，助力经济高质量发展。
中小企业融资难一直是我国学术界关注的热点问题，有大量相关研究(李伟和成金华，2005；王东静和张祥建，2007；王弟海，2011；吕劲松，2015；王馨，2015；陈道富，2015；余大胜，2017；钱雪松等，2019；田国强和赵旭霞，2019)从信息不对称、金融市场不完备、银行垄断与利率管制、法律制度等角度探讨了我国中小企业融资难的原因，尝试提出法治建设、 产业政策、 财政和金融体制改革等多方面的建议。这些研究一个共同特点是倾向于研究中小企业融资难的外部原因，往往忽略对企业特别是创新型中小企业自身特点及其在融资难题产生过程的作用的研究，这显然不利于理解创新型中小企业与其它普通中小企业在融资难问题上的差异，从而难以提出更加具有针对性的政策建议。
基于上述考虑，本文构建一个中小创新型企业创新过程的数学模型，分析中小创新型企业的融资难问题。在现实经济中，创新型中小企业往往无法获得长期的融资，相当多数企业不得不依赖于短期债务(Short-term Debt)持续经营，而这一融资方式伴随着高度的展期风险(Rollover Risk)：在企业借新债还旧债的过程中，融资成本可能随债务的展期而提高。展期风险与企业从事的业务密切相关：传统的有稳定现金流的企业，能比较顺利地实现下一步融资，展期风险不会太大；而对于创新型中小企业而言，企业的融资能力很大程度上取决于研发创新结果。这说明除了以往文献中提及的因素外，债务结构也是影响中小创新型企业融资的一个重要因素，因此，本文控制了信息不对称及外部融资环境等因素，通过泊松学习模型化新兴项目收益的不确定性，抓住创新型中小企业倾向于依赖短期债务这个关键特征，重点研究这种债务结构带来的展期风险及其对创新型中小企业融资的影响。
本文考虑的是一个动态多期模型，企业每期需要运用短期债务为其风险性创新项目融资，分析的风险性创新项目与普通的有风险的投资项目的最主要区别在于弗兰克·奈特所提出的“风险”(Risk)与“不确定性”(Uncertainty)之间的差别。普通的风险投资虽然存在收益上的风险，但其收益的分布较为明确，体现为收益围绕项目的基本面波动。这种投资的收益虽然有风险却不具有不确定性。与普通的风险投资不同，由于创新型项目是新生事物，其收益往往具有不确定性，换句话说“收益的分布”是不确定的。本文采用泊松学习(Poisson Bandit)来模型化创新型项目的基本面不确定性，因此该项目面临着两方面的风险。首先，该项目每一期的现金流是不确定的(为简化模型，假设现金流要么为某个正数要么为零)。其次，企业每一期产生正的现金流的概率在初始时刻也是未知的。依据这些风险提出的假设的重要性在于，如果企业产生正的收益的概率是确定的，或者更进一步的，企业的现金流是确定的，市场对企业的盈利能力和企业家的违约行为会有一个稳定的预期。此时，企业的融资成本也会较为稳定，展期风险不会太大。在概率未知的情形下，企业家与投资人需要从研发创新的结果中逐步学习(Learning)这一概率的大小。特别地，当企业创新失败时，市场会下调对企业盈利能力的预期，上调对企业违约的预期，进而提高企业的融资成本和展期风险。
为简化分析，假设企业每期需要的投资都是1元，企业和投资人都是风险中性的，同时企业以往短期债务的收益或损失完全由企业的股权所有者承担。最后这个假设使我们只需关注企业每期在固定的1元投资上的违约问题。在市场的竞争性均衡中，投资人如果投资于该企业，其预期收益必等于市场的外部回报；同时，企业每期会根据研发创新的结果决定是否违约并终止项目。如果该项目的净价值(扣除展期费用之后的企业价值)为正，企业将会对短期债务进行展期；如果该项目的净价值为负，企业将会违约。
本文在上述设定下比较了竞争性均衡下的企业研发创新行为和社会最优的研发创新行为。在竞争性均衡下，创新的不确定性和企业对短期债务的依赖自然而然地衍生出展期风险。当研发结果不尽如人意时，市场对企业盈利能力的信念降低，企业融资成本上升。当融资成本足够高时，违约成为企业的最优选择。这将导致融资环境的恶性循环：一方面，预计到企业违约的可能，贷款人会要求较高的回报以补偿其所承担的风险。另一方面，贷款人对企业违约的理性预期提高了企业的融资成本，导致企业更容易违约。
由于融资成本随信念变化，竞争均衡下企业的价值可能是信念的一个非连续函数。注意到企业的价值是决定企业家是否违约的关键，企业家的值函数是本文模型分析的关键。本文采用猜解加求解差分方程的方法，完全显式地刻画出竞争均衡下企业的值函数。基于该值函数，进一步刻画均衡时企业的研发创新行为，发现相比于社会最优的研发创新决策，竞争均衡下的企业总是过早地结束创新项目，导致社会福利的损失(体现为竞争均衡下的企业价值低于社会最优时的企业价值)。本文还发现社会最优时的企业价值是市场对企业盈利能力的信念的一个连续函数，而竞争均衡下的企业的值函数是分段的，会根据企业的研发结果发生“跳跃”。特别地，每当企业研发创新失败时，企业的价值都会有“断崖式”的下降。
上述理论分析的结果与现实中中小创新型企业融资难问题有很密切的联系。本文的结论表明中小企业融资难一方面是因为中小企业很多投资于研发创新型项目，面临的风险比较高；另一方面是因为中小创新型企业对短期债务融资的依赖。因为展期风险的存在，使得一些本应获得融资的企业无法获得融资，而即便有些企业能获得融资，也需要支付较高的融资成本。因此，当研发创新结果不尽如人意时，企业会早早地选择违约并结束创新项目。
本文的主要贡献有两个方面：一方面，据我们所知，还没有文献同时直观地刻画融资环境的“恶性循环”和企业价值的“跳跃”这两项特征。本文丰富了有关创新型企业融资问题的微观基础，在此基础上可以研究创新型企业的融资策略、投资人的投资策略以及政府如何防范有关的金融风险。另一方面，本文讨论了如何采用长期融资策略以化解展期风险，提高资源配置的效率。尽管以往的实证和理论研究已经充分说明了诸如权益性融资更有利于创新型企业的发展(Hsu et al.，2014; Tian,2012)，但是现实经济中的中小企业很依赖于债权性融资。因此，分析如何制定长期融资契约以避免展期风险带来的损失具有现实意义。本文提供了一种可以实现社会有效配置的长期融资策略：投资人可以根据期初的信念制定本轮融资的期限，并且在本轮投资之初收取一定的佣金，以降低本轮最后一期的融资成本。通过这样的安排，可以提高企业违约的机会成本从而降低展期风险，有效地避免恶性循环问题，达到双赢的结果。
本文研究我国中小企业融资难问题时，构建了一个外部融资下的企业研发创新模型，因而与这类文献密切相关。这类文献多基于企业家与风险投资人或债权人间的委托代理关系研究企业创新活动。有些文章侧重于分析当企业家(代理人)可以自由决定项目停止时间时，创新型企业的风险投资人(委托人)如何提供激励，让代理人从事创新活动(Dewatripont和Maskin, 1995; Qian和Xu, 1998; Bergemann和Hege, 1997，2005; Cornelli和Yosha, 2003; Manso, 2011; Hörner和Samuelson, 2014; Halac et al., 2016)。这些文献常用指数学习(Exponential Bandit)来模型化创新结果的不确定性，而本文采用了更一般化的泊松学习(Poisson Bandit)来模型化创新结果的不确定性。另有一部分文献假定代理人可以用违约来威胁委托人，并研究该策略性违约行为对委托人借款决策的影响(Hart 和 Moore, 1994, 1998; Bolton和Scharfstein, 1996; Fluck, 1998; DeMarzo和Fishman, 2007)。Hart和Moore(1994)在一个确定性模型中发现当项目的持续需要企业家才能，而企业家可以用收回自己在项目上投入的人力资本来威胁债权人修改债务协议时，一些原本有价值的项目将无法被实施。本文与这类文献的不同是，在收益不确定的动态学习环境下，分析了展期风险与违约行为间的相互强化作用及其对均衡有效性的影响。
与本文相关的第二类文献自然是研究展期风险的文献。尤其是短期债务的展期风险是如何与2007-2009年金融危机中市场的突然冻结(Sudden Stop)联系到一起的(Brunnermeier et al.，2009；Acharya et al.，2011；He和Xiong，2012a，2012b；Bouvard et al.，2015；Eisenbach，2016)。Leland(1994)、Leland和Toft(1996)讨论企业的收益具有不确定性时，最优的债务期限结构和内生的违约行为。在此基础上，He和Xiong(2012a)引入债券交易的二阶市场，分析了债券的流动性溢价和违约溢价间的交互关系，发现流动性冲击导致的债券价格下降会使得股东在企业基本面较好的情况下选择破产以避免展期损失，从而进一步恶化债券市场的流动性。同样是考虑展期风险对债券市场的影响，He和Xiong(2012b)从债权人的角度出发，强调了企业基本面波动性的作用，发现基本面价值波动带来的企业展期风险会使债权人选择先发制人的策略，导致企业负债能力的下降。与此相对，Acharya et al.(2011)在企业基本面价值的均值和波动性不变的情况下，指出决定展期风险的是：相对于企业再融资的速率，有关企业盈利能力的信息的到来速度。与本文不同的是，这些文章大多假设一个外生的随机过程来引入收益的不确定性，但企业的基本面是确定的。这与研发创新型企业实际情况有所不同，因为研发创新过程中企业的基本面往往是不确定的，可能是高收益项目也可能是低收益项目。因此，本文中展期风险发生作用的机制是企业家和债权人关于该项目为高收益项目的信念随着研发结果而变化，而当研发结果不佳时，市场会提高对企业违约的预期和相应的融资成本，使得企业提早结束研发。
二 模型构建与分析
本文研究了一个无穷期的离散时间模型。该模型中有两类风险中性的个体：企业家和投资人。企业家管理有风险的创新型项目，该项目将在每期期末产生R
∈{0,X
}的现金流，其中X
>0。该项目的基本面由参数θ
∈{θ
,θ
}描述，它表示项目在t
期产生X
的现金流的概率，亦即Pr
(R
=X
|θ
)=θ
，0<θ
<θ
≤1。因此θ
在模型中反映了企业的盈利能力。为简化分析，假设θ
+θ
=1。另外，给定参数θ
，项目每期的回报是独立同分布的。企业的贴现率为β
，目标是最大化创新型项目的净期望收益，为此每期开始时企业需要决定是否继续投资该项目。为延续该项目，企业每期期初需要从外部融资1元并投入研发，假设这笔融资只能通过短期债务的方式实现。如果企业在第t
期期末决定继续这一项目，则需要首先对本期期初发行的短期债券进行还本付息，这笔总费用就是第t
期的融资成本。竞争性的借贷市场上有一个短期存在的投资者，该投资者每期拥有1元资金，且存在某个外部投资(比如将钱存入银行)可以确定性地在期末带给他c
>1的收入。在竞争性市场上，企业债务的面值应使得投资人在该项目与外部投资间无差异。假设θ
X
>c
>θ
X
，因此θ
=θ
时社会的最优选择是放弃该项目，而θ
=θ
时社会的最优选择是继续实施该项目。在初始时刻，企业家和投资人都不知道创新型项目的基本面θ
，但是企业历史的现金流是可被完美观测的。企业家和投资人会根据企业历史的现金流来更新关于θ
=θ
的信念。当企业获得X
的现金流时，企业家和投资人关于θ
=θ
的信念提高或不变，反之则下降或不变。与有关文献一样(He和Xiong，2012a)，本文假设股权持有人为展期收益或损失的剩余索取者：任何新增收益会被马上支付给股权持有人，且任何新增损失将通过以市场价增发股票的方式即时支付。另外，由于本文关注的是展期风险对企业研发创新行为的影响，假设企业家的目的就是最大化股东的利益，而不考虑企业家与股东间的利益冲突。由于不需要发行新的企业债来弥补展期的损失，上述假设将简化分析，使得我们只需关注于企业每期在固定的1元投资上的违约问题。假定如果企业不违约的话，则下一期可以继续获得1元的投资，一旦违约，则永远获得零的收益。若企业家决定增发股票来支付融资成本以避免企业破产，则股东可能从企业未来的创新中获益。同时，这一费用将反馈回企业的股价，体现为企业价值的下降。反之，一旦违约，股东可以节省融资成本，但企业未来的收益将为零。这是本文建模的关键：企业价值由企业的基本面(项目的期望价值)和期望的融资成本共同决定，一旦违约，企业未来将获得零的收益。只要项目的期望价值大于融资成本，企业家就愿意向债权人支付融资成本，从而延续项目。若企业在t
-1期还未违约，其在t
期的收益为：
F
为企业在t
期的融资成本(即债券面值)。假定F
是在t
期期初被决定的，且不随企业的现金流大小而调整。以银行贷款为例，企业的贷款利率与它的经营业绩无关。总结而言，当前一期企业选择继续研发时，可以用图1来描述在某一期中相继发生的事件。
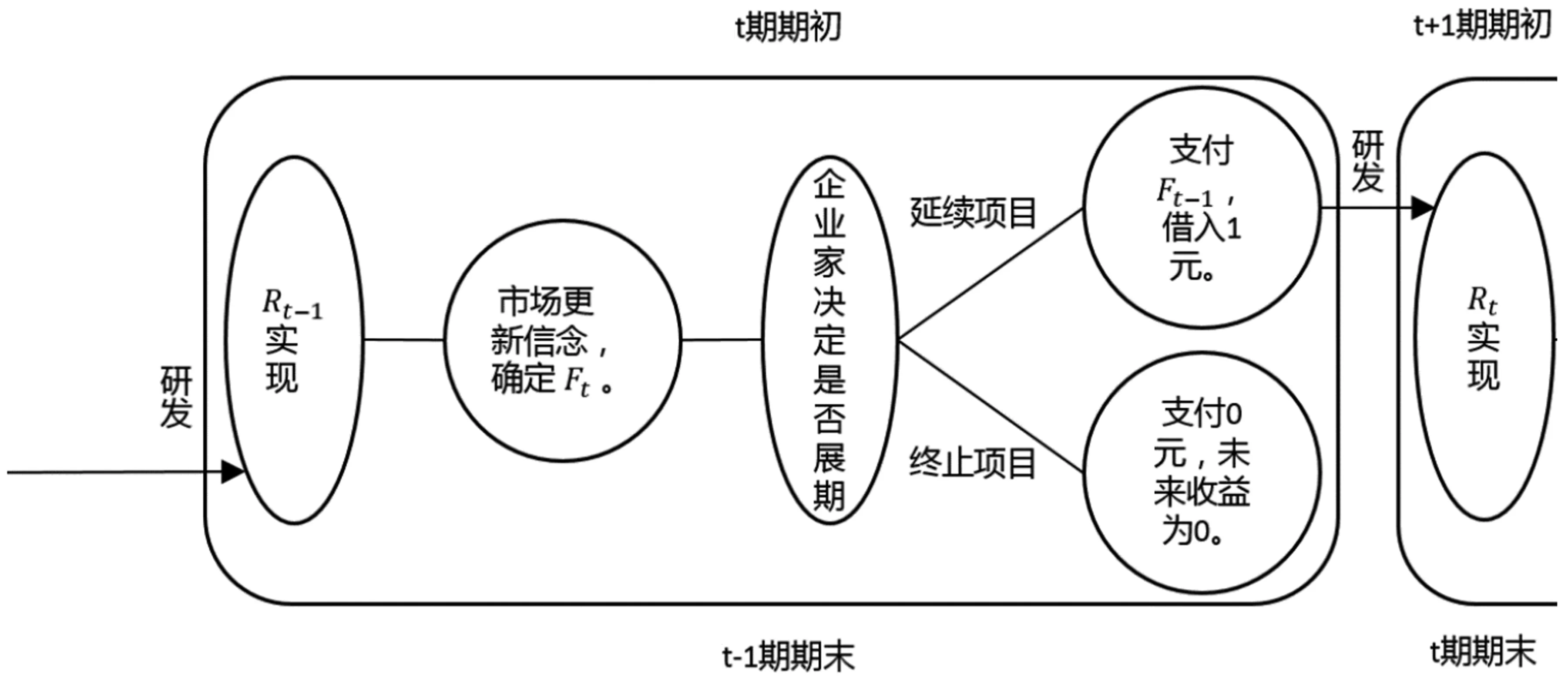
图1 时间轴
需要说明的是，大方圈里面的事件发生在同一时刻，既是t
期期初也是t
-1期期末。在t
期期初，t
-1期的研发收益R
-1实现，市场随之更新对企业的信念，并确定企业在t
期的融资成本F
。跟着企业家根据信念和融资成本决定是否展期并延续项目。如果企业决定研发，则需要首先偿还上一期借款的成本F
-1；反之，若企业放弃研发则可以节省下融资成本，但同时未来收益变为0。若t
期期末企业选择继续研发，则同样的事件将在下一方圈中重演。(一)均衡定义
首先定义模型中的均衡。在均衡定义中，一个非常重要的元素是市场参与人关于θ
=θ
的信念。该信念的更新服从贝叶斯法则。给定t
期期初市场参与人关于θ
=θ
的信念ρ
(简称为事前信念)以及t
期的现金流R
，根据贝叶斯法则可得t
期期末θ
=θ
的信念ρ
′(简称为事后信念)：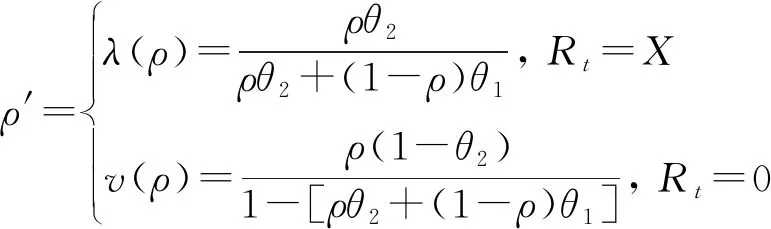
(1)
需要说明的是，在假设θ
+θ
=1下可得λ
(v
(ρ
))=ρ
：从信念ρ
出发，如果市场获得一个好信号X
和一个坏信号0，则关于θ
=θ
的信念保持不变。另外，设第1期的事前信念严格介于0和1之间，因此有限期后的事前信念也严格介于0与1之间。一般而言，t
期企业面临的融资成本以及企业的违约决策同时取决于事前信念ρ
以及时间t
。本文的分析限制于马尔科夫(Markov)策略：企业面临的融资成本以及企业的违约决策都与时间t
无关。这是一个非常合理的限制，因为无论在什么时间，只要市场对企业盈利能力的信念是相同的，使得投资人在投资于该风险项目与外部投资间无差异的企业债务面值应该是相同的。马尔科夫策略的假设使得本文可以把企业的值函数写为信念ρ
的函数。若企业在t
-1期还未违约，给定t
期初始信念ρ
，R
实现前企业的值函数可表示为：V
(ρ
)=[ρθ
+(1-ρ
)θ
]U
[λ
(ρ
)]+[1-ρθ
-(1-ρ
)θ
]W
[v
(ρ
)](2)
其中:U
(ρ
′)=max{X
,X
-F
(ρ
)+βV
(λ
(ρ
))}，W
(ρ
′)=max{0, 0-F
(ρ
)+βV
(v
(ρ
))}。这里的F
(ρ
)是初始信念等于ρ
时企业的融资成本。如果项目成功并带来X
的现金流，企业家需要决定是否违约，违约时即得到X
的净收益，不违约时的收益为X
-F
(ρ
)+βV
(λ
(ρ
))。类似地，研发失败现金流为零时企业家同样需要决定是否违约。违约时可以节省下融资成本，但企业未来的收益将为零。不违约时，企业家则需增发股票来支付融资成本以避免企业破产，但可能从企业未来的创新中获益，这部分价值为βV
(v
(ρ
))。上述表达式体现了本文建模的关键：企业净价值由企业的基本面(项目的期望价值)和融资成本共同决定。当且仅当项目的期望价值大于融资成本时，企业家愿意向债权人支付融资成本，从而延续项目。用q
(ρ
)表示初始信念为ρ
时市场预期的企业违约概率。由于投资人是竞争性和短期的，q
(ρ
)<1时，企业的融资成本F
(ρ
)必然满足投资人在投资于该风险项目与外部投资间无差异。[1-q
(ρ
)]F
(ρ
)=c
(3)
同时，假定当q
(ρ
)=1时，投资人不会借钱给企业。本文始终关注的是竞争性市场均衡(简称均衡)。该均衡的正式定义为：
定义1：在一个竞争性市场均衡中，下列条件必须得到满足：(1)在任意事前信念ρ
下，只要投资人向企业提供1元融资，方程(3)必须满足；(2)企业的值函数满足方程(2)；(3)t
期期末的现金流R
实现以后，企业作出最优的违约决策；(4)企业最优决策下导致的违约概率与市场预期企业违约的概率q
(ρ
)相等。上述定义与竞争性市场均衡的标准定义相一致。一方面竞争性的投资人预期利润为零；另一方面，企业在每期采取最优的违约决策。最后，本文还要求市场对企业违约概率的预期是理性的，也即与实际的违约概率相等。
(二)均衡分析
给定上述竞争性市场均衡的定义，本文还是无法完全排除一些奇怪的自我实现均衡：比如当ρ
比较高时，市场反而预期企业的违约概率会比较高。因此，在本部分的均衡分析中，只考虑单调均衡。在该均衡下企业采取截断策略，即存在截断点ρ
使得企业的违约决策完全取决于事后信念ρ
′是否小于ρ
。当且仅当事后信念ρ
′≤ρ
(也即企业认为其盈利能力比较差)时企业会选择违约。这里的ρ
是在均衡时决定。下列定理表明，给定ρ
，可以唯一地确定满足方程(2)的企业的值函数V
(ρ
)。
V
(ρ
)=A
ρ
+B
,ρ
∈(ρ
,ρ
+1]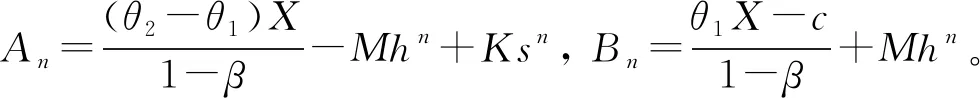
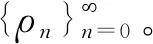
ρ
,ρ
]内时，企业的价值为：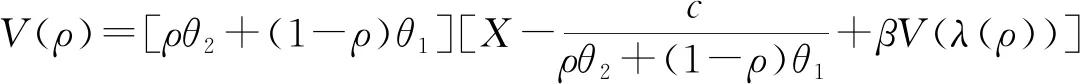
(4)
而当事前信念ρ
>ρ
时，企业的值函数为：V
(ρ
)=[ρθ
+(1-ρ
)θ
][X
-c
+βV
(λ
(ρ
))]+[1-ρθ
-(1-ρ
)θ
][-c
+βV
(v
(ρ
))](5)
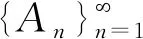
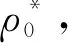
(6)
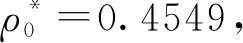
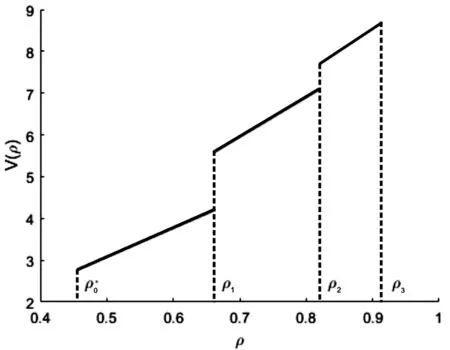
图2 均衡时值函数
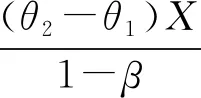
综上，短期债务带来的展期风险对于企业违约还是继续研发创新的决策有着重要影响。由于这一风险，企业会在社会有效决策为继续研发时结束研发。展期风险也使得企业在面临是否要违约的决策时值函数出现大幅的跳跃。当项目失败时，受展期风险的影响，企业的值函数会经历断崖式的下降。
(三)社会最优配置
本部分将明确地刻画社会最优的研发决策。这一问题可以看作是社会计划者在任意给定信念下决定是否继续研发。若社会计划者决定继续研发，则必须承担研发成本c
，而得到的现金流要么为X
要么为0。结果，社会计划者的值函数为：S
(ρ
)=-c
+[ρθ
+(1-ρ
)θ
][X
+β
max{0,S
(λ
(ρ
))}]+β
[1-ρθ
-(1-ρ
)θ
]max{0,S
(v
(ρ
))}(7)
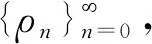
S
(ρ
)=V
(ρ
)=A
ρ
+B
,ρ
∈(ρ
,ρ
+1]这个结果看似有点奇怪，因为社会最优的值函数与在定理1中描述的企业的值函数一致。事实上，只有两种情况下的ρ
相等时两者的值函数才会相等。但由于这两种情况下的边界条件不相同，ρ
的取值也不相等。在上一部分描述的均衡中，ρ
是由企业的无差异条件F
(ρ
)=βV
(ρ
)确定的。因此，创新研发在事后信念还很高时就停止了。在社会有效的配置下，截断点ρ
是根据S
(ρ
)=0得到的。这意味着：-c
+[ρ
θ
+(1-ρ
)θ
]X
+β
{A
ρ
θ
+B
[ρ
θ
+(1-ρ
)θ
]}=0进而可得社会有效的截断点满足：
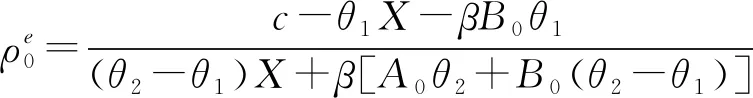
c
、现金流的大小X
和优质项目产生现金流的概率θ
而变化的。图中，效率的截断点总是在0.1左右，而均衡的截断点则在0.4左右。从中可以发现竞争性均衡下企业停止研发的截断点要更大，因此竞争性均衡下的企业更可能放弃研发。这是因为展期风险恶化了企业的融资环境，降低了违约的机会成本，结果带来了巨大的社会无谓损失。
图3 截断点随x、θ2和c的变化
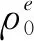
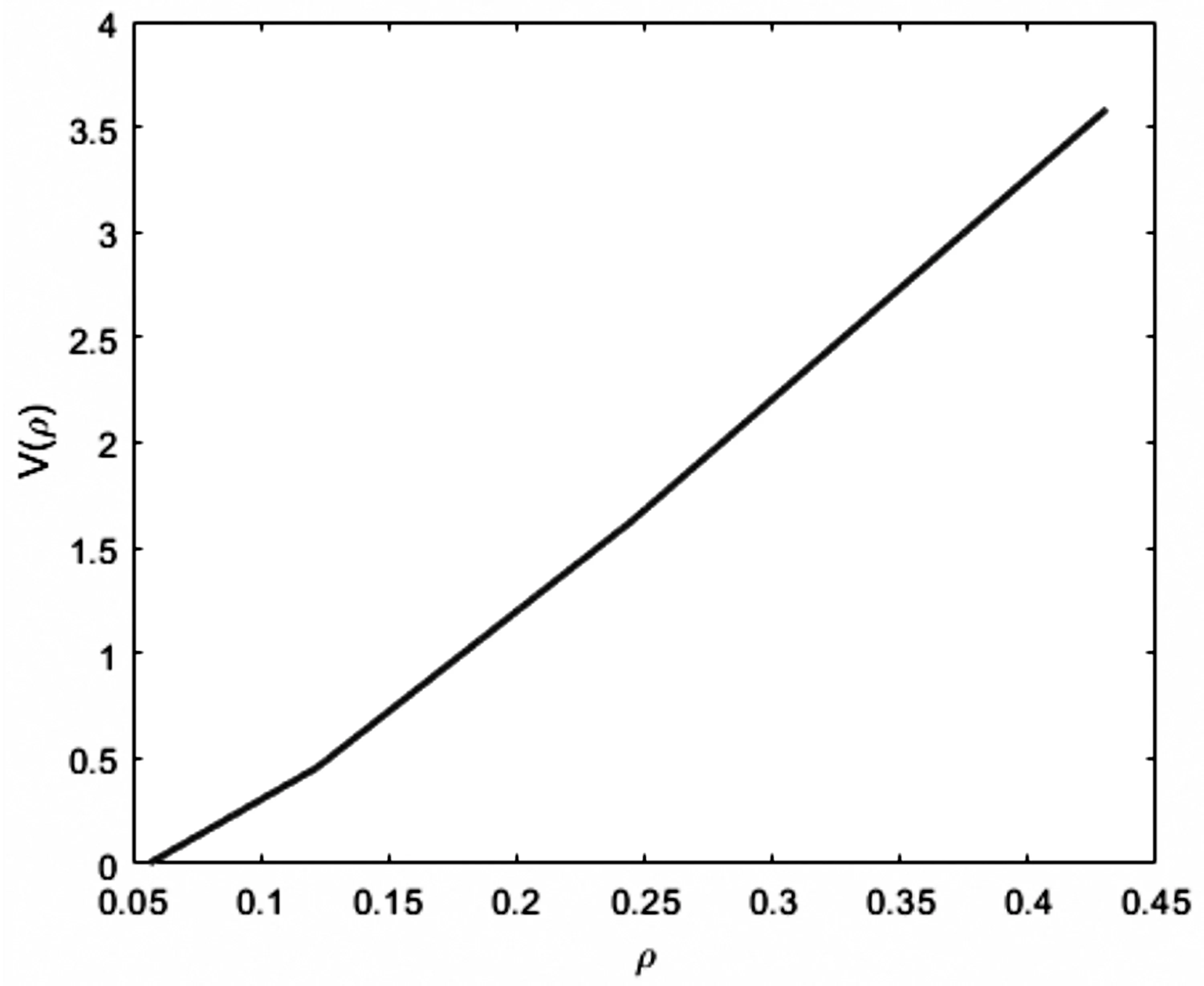
图4 社会有效的值函数
(四)长期融资契约
前文证明短期融资下的竞争均衡是没有效率的，本部分尝试说明采用某些精心设计的长期融资契约可以实现社会最优配置。为了引入长期融资安排，本文放松之前的短期投资者假设：投资者存活无穷期，并面临r
的市场利率。在一个竞争性的市场中，投资者可以承诺提供长期融资契约，并得到0的预期利润。
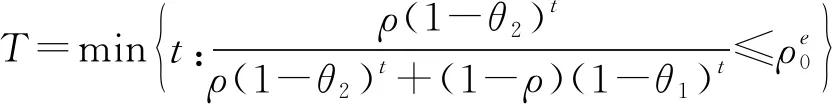
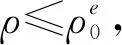
T
期不需向投资者偿还所借的1单位研发资金，但是其在本轮投资之初支付的佣金已经完全补偿了投资者。而且这个设计正好弥补了短期融资的问题。注意到在前文分析的短期融资下的竞争均衡中，企业家在最后一期之前所有期都不会违约而仅仅只会在最后一期违约，而违约的可能性导致投资者索要更高的补偿，又使得企业更容易违约，从而引发一个恶性循环。在上述长期融资契约设计中，因为最后一期无论企业研发成败与否都不需要支付任何费用，上述问题被有效地避免，从而能实现社会最优配置。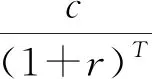
三 结论与启示
本文理论分析中的企业主要指现实中的初创型中小企业，这些企业在创业初期往往并不清楚自己投资的项目能否成功或者盈利水平是多少。因此，本文的理论分析结果与现实中创新型中小企业融资难问题有很密切的联系。由于创新型企业的基本面具有不确定性，又由于企业可能在业绩不佳时选择违约，企业融资成本会随着市场对企业盈利能力的信念而变化。特别地，当创新的结果不好时，融资成本随着企业违约可能性的提高而提高，而较高的融资成本又使得企业在项目的社会价值大于零时结束研发并违约。这一恶性循环使得竞争均衡的结果变得没有效率。上述结论表明，企业不能承诺履约时，以短期债务融资的中小创新型企业将面临展期风险。而中小企业融资难问题与这一债务结构息息相关。在短期债务融资之下，因为展期风险的存在，一方面使得有一些本应获得融资的企业无法获得融资；另一方面即便有些企业能获得融资，也需要支付比较高的融资成本。当研发创新结果不尽如人意时，企业会早早地选择违约并结束创新型项目。因此，在解决中小企业融资难问题时，不仅仅要着眼于企业是否能获得贷款(例如通过定向降准的方式为中小创新型企业提供精准的融资优惠)，同时还应关注企业的债务结构问题。
另外，本文还发现展期风险下企业的值函数是一个分段函数。当差的研发结果发生时，企业的价值会向下跳跃，且信念越低，跳跃的幅度越大。与此相反，社会有效的值函数关于信念是连续的，说明在社会最优的情况下不存在展期风险。值函数的突然跳跃说明展期风险下企业的价值是不稳定的，这一不稳定性可能反馈到金融市场中。例如企业债券价格随展期风险提高而大幅下降时，债券市场的流动性可能因债券价格的下降或不稳定而受损，严重时可能导致系统性风险。
最后，本文还给出了一种长期融资安排来应对展期风险。这一融资安排的核心是提高企业信念较高时候的融资成本，降低企业信念较低时候所需支付的展期费用，从而在维持投资人收益的情况下，提高企业违约的机会成本，降低展期风险。相对于短期融资，这一长期融资契约下展期风险更小，最终的均衡要更加有效。在现实经济中，企业存在违约风险时，债权人可能希望通过短期投资的方式降低投资无法收回的风险。本文的结论则说明，债权人这种“走一步，看一步”的做法很可能不是最优的。通过设立更加长期的融资契约，债权人与企业可以达到双赢。这一融资策略不同于股权融资，却是有效的，说明在无法取得股权融资时，为中小企业提供精心设计的长期融资契约也能在很大程度上帮助企业解决融资难问题。
需要说明的是，虽然本文将中小创新型企业融资难问题作为模型在现实中的对照，文章中的模型也可用于分析其他具有下列特征的问题：(1)企业的基本面具有不确定性；(2)企业或投资人根据企业以往的业绩更新关于企业基本面的信念；(3)融资成本受企业业绩的影响。这些情况在现实中极为普遍，且通常均会产生不同程度的展期风险。本文为研究这类问题建立了一个微观基础。
本文之后还有许多可以拓展的研究主题。例如，展期风险下创新型企业如何进行最优的股权或债权融资。本文虽然给出了一项长期融资策略，但是可能还存在其他有效的融资方式。未来可以考虑基于企业信念和业绩的融资方式，分析最优的投融资策略。其次，也可以研究中小企业能否联合向银行融资，共同承担融资成本，降低整体的展期风险。再者，还可以考虑政府如何通过政策工具缓解中小创新型企业因展期风险导致的融资难问题。最后，还可以分析金融监管机构如何应对由展期风险带来的股市波动。
猜你喜欢
教育家(2022年18期)2022-05-13
齐鲁艺苑(2022年1期)2022-04-19
雪豆月读·低年级(2020年7期)2020-09-10
科学导报(2019年39期)2019-09-03
学苑创造·A版(2017年11期)2018-01-23
学生天地·小学中高年级(2009年11期)2009-12-15
作文成功之路(初中)(2008年12期)2008-12-29
青年时代(2006年11期)2006-07-18
