基于混合聚类与融合用户兴趣的协同过滤推荐算法*
麻 天 ,余本国 ,张 静 ,宋文爱 ,景 昱
(1.中北大学 软件学院,山西 太原 030051;2.山西省军民融合软件工程技术研究中心,山西 太原 030051;3.海南医学院 生物医学信息与工程学院,海南 海口 571199)
0 引言
在信息快速发展的现代社会中,推荐算法已经普遍出现在人们的生活中,给人类生活无形中带来巨大便利[1],如短视频推荐[2]、音乐歌曲推荐[3]、新闻信息推荐[4]。协同过滤推荐算法在工程上更容易实现。该算法分为两类:基于用户的协同过滤推荐算法(user-based collaborative filtering)和基于项目的协同过滤推荐算法(item-based collaborative filtering)[5]。简言之:物以类聚,人以群分。虽然协同过滤推荐算法与其他推荐算法相比有很多优点,但解决推荐效率低、推荐质量低、冷启动和稀疏矩阵等问题一直是研究者不断努力改进的方向[6]。其中在计算不同用户之间的相似性时也存在很多问题,相似度计算不精准是影响推荐准确性的一个关键因素[1]。
很多研究学者提出很多方法改进以上存在的问题。赵伟等在传统K-means 聚类算法的基础上做了改进,有效地解决了有关用户聚类的一些问题[7]。王蓉等提出了一种混合聚类与融合属性特征的协同过滤推荐算法,在一定程度上能提高推荐效率,解决冷启动问题,为聚类算法在推荐系统中的研究开辟了新思路[6]。
本文依据上述学者的思路,改进了算法,通过建立Canopy+bi-Kmeans 混合聚类模型[8]和一种改进的相似度计算方法,提出一种基于混合聚类与融合用户偏好的协同过滤推荐算法,从而可以达到提高推荐可靠性、提高推荐精度的效果。利用MovieLens 数据集进行试验得出结果表明,该算法不仅能有效解决存在的冷启动问题,而且可提高推荐算法效率。
1 Canopy+bi-Kmeans 混合聚类算法
1.1 Canopy 算法
首先利用Canopy 算法对数据集进行一次聚类,这种算法有利有弊,不需要指定k 值,可以快速得到聚类簇,但是精度较低[9]。算法过程如下:
(1)从原始数据中生成样本列表X=[x1,x2,…,xm],在设定初始距离阈值T1、T2时,通过两种方式调整参数:先验知识和交叉验证,且T1>T2。
(2)选取Canopy 质心。从列表X 中任选一个样本,令第一个样本为P,并将P 从列表中删除。
(3)从列表X 中随机选取一个样本R,计算R 到所有Canopy 质心的距离,判断其中最小的距离D:如果D≤T1,则令R 为一个弱标记,表示R 属于该质心,并将R 加入其中;如果D≤T2,则将R 进行强标记,表示R 属于该质心,更新强样本标记质心,并将样本R 从列表X 中移除[10];如果D>T1,则R 形成一个新的聚簇,并将R 从列表X 中删除。
(4)若列表X 中元素个数不为零,则不断重复上述步骤(3)。
1.2 bi-Kmeans 算法
bi-Kmeans(bisecting K-means)聚类算法受随机选择初始质心的影响比较小,改进K-means算法随机选择初始质心的随机性造成聚类结果不确定性的问题。简言之:“高内聚,低耦合”。意思是让每个类簇之间要有明显的界限,类簇内部的点要团结紧凑[11]。bi-Kmeans 算法步骤如下:
(1)从原始样本集合中随机取k 个初始中心点。
(2)以这k 个中心点为标准,计算所有样本点到中心的距离,计算后将其加入到距离最近的类簇。这样每个样本都有自己的簇了。
(3)重新计算每个簇中的样本中心点,如果中心点未发生变化转到步骤(4),发生变化回到步骤(2)。
(4)得出结果。
输出:划分出的聚类簇以及聚类中心。
在选择聚类时,利用SSE(Sum of Squared Error)当作度量聚类效果的指标。不同聚类算法对比见表1。
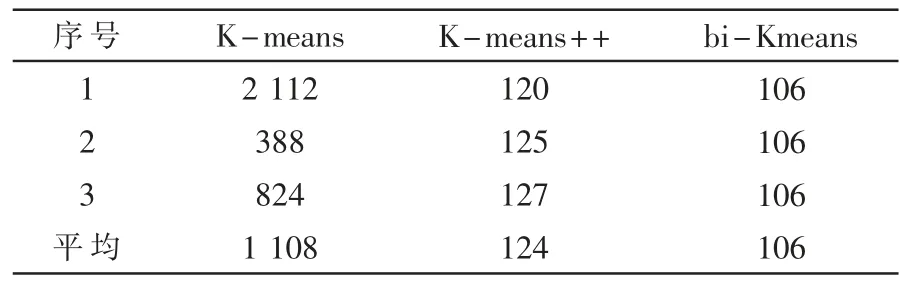
表1 不同聚类算法对比
从表1 以直观地发现,bi-Kmeans 计算出来的SSE值最小,并且趋于稳定值,说明聚类的效果也最好。因此,本文选用bi-Kmeans 这个聚类方法。
1.3 Canopy+bi-Kmeans 算法
Canopy+bi-Kmeans 这个聚类组合有很多优点,如增强了单独聚类抗干扰的能力,加快了相似性计算的速率。Canopy+bi-Kmeans 算法流程图如图1 所示。
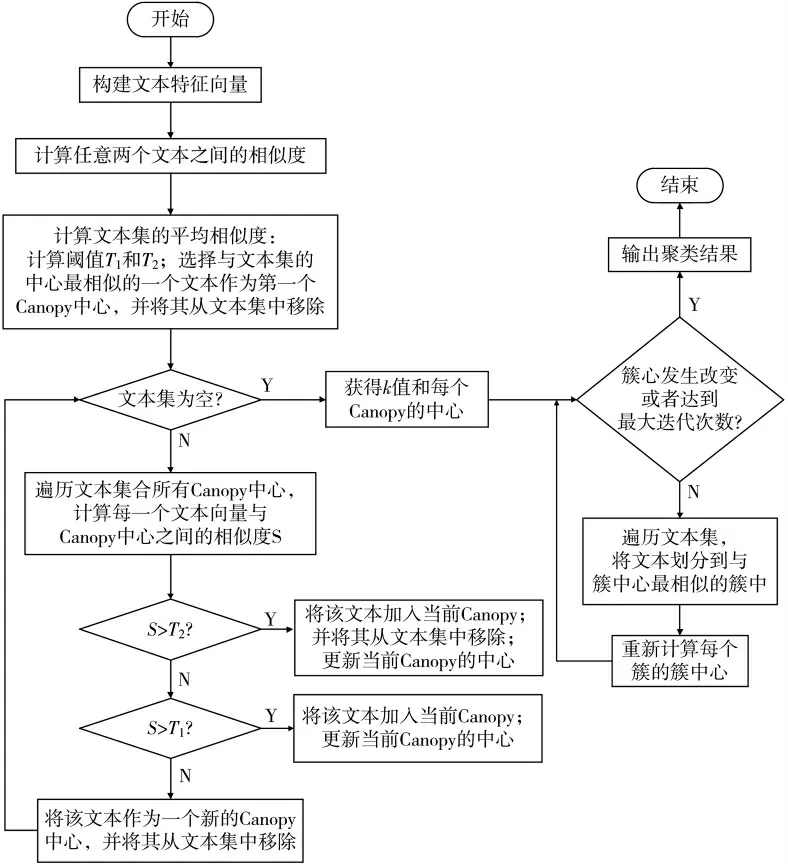
图1 Canopy+bi-Kmeans 算法流程图
2 计算用户偏好相似性
2.1 计算用户偏好
通常用户会根据个人的兴趣对项目打分。文献[12]简单地根据标签的数量来判断用户的偏好,从而使得当前潮流标签权重过高使得某些用户选择冷门标签时无法得到更准确的推荐,未能将用户的兴趣偏好充分展现出来。这对上述问题,本文利用TF-IDF 的方法对用户偏好进行计算。
TF-IDF 用计量统计的方式来评估某个关键词在其所在的语料库中的重要性[13],公式如下:
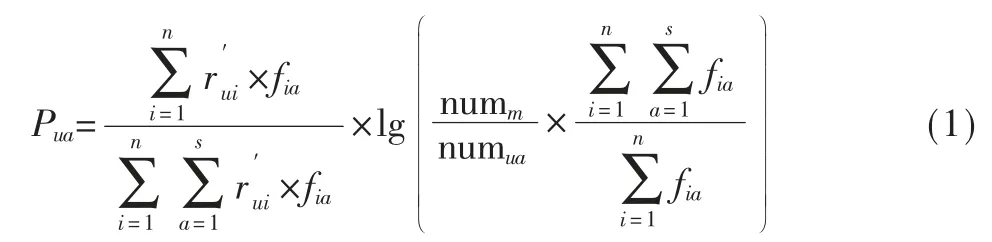
其中,Pua表示用户u 对项目标签a 的偏好值,Pua值与偏好程度成正比;n 表示项目总数,s 表示项目标签总数;表示用户u 标注标签a 的次数,表示用户u 标注的总次数;numm表示用户总数,numua表示标注过标签a 的用户数;表示标签总数,表示标签a 的总数。
由式(1)可以看出,用户选择的标签被用户选得少并且此标签占整个标签集合的比重越小,这样就能在一定程度上明确用户偏好,从而提高推荐效率。
2.2 融合时间系数的衰减函数
传统的推荐算法对用户标签偏好常用静态标签标识,一般用0 和1 来表示。这样可以明显看出在任何时候这些标签所起到的推荐作用都是相同的,对于某些时效性较强的推荐并不能起到较好的推荐效果。例如:某用户以前喜欢古典音乐,现在喜欢流行音乐,如果不考虑用户兴趣偏好随时间变化就会导致推荐不贴合用户偏好[14]。在实际中用户的兴趣往往是处于动态变化中的[15]。相对于早期的用户行为,近期的用户行为对于推荐更有意义,因此将用户近期的标签给予较高的权重,从而使推荐更具有时效性,提高推荐效率。本文引入一种衰减函数并且融入时间系数来充分贴合用户兴趣偏好随时间的变化,公式如下:

其中,Tui∈(0,1),代表用户u 对项目i 的时间权重;Ts表示时间窗口参数,其值表示用户偏好兴趣持续时间;tnow表示当前做推荐的时间,tui表示用户对项目作出评价的时间;Tatt是时间衰减参数,代表兴趣偏好衰减速率;表示对计算结果进行上舍入处理,Ts×表示用户评价项目时间所处的时间段。若用户在一周的时间内兴趣偏好基本没变,则认为该用户兴趣保持稳定的周期为7 天,即Ts=7。若用户评价完项目后在7 天内进行推荐,即tnow-tui≤7,则用户兴趣在第8 天后才开始衰减,每7 天为一个衰减周期,衰减周期内衰减系数相同。
2.3 计算用户偏好相似性
根据前文分析,在利用TF-IDF 方法计算用户兴趣偏好时加入融入时间系数的衰减函数得出用户兴趣偏好,更新用户标签矩阵中的值,公式如下:
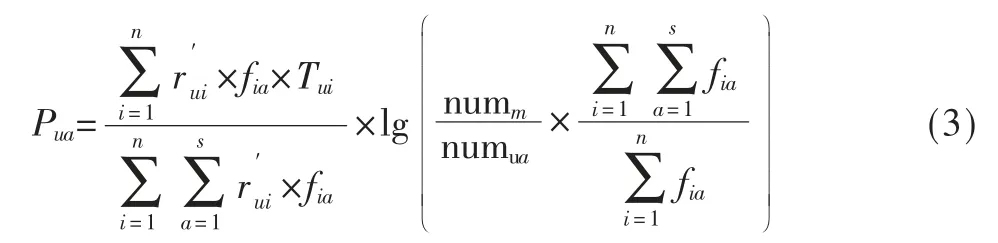
最后归一化欧式距离,公式如下:
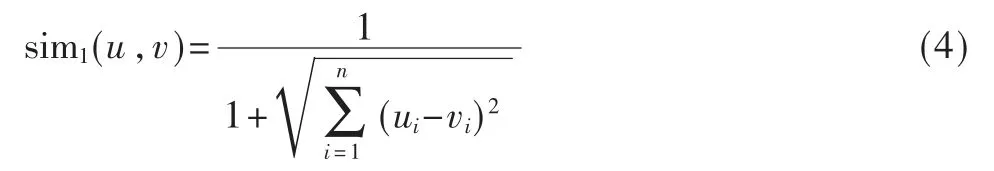
2.4 融合用户属性相似度
在计算相似度时,采用常规的相似的算法不会将不同用户的个人属性进行相似性对比,如性别和年龄等属性。因此,本文考虑了上述用户属性,并且将这些基本的用户属性融入到相似度计算中。
(1)年龄属性相似度,公式如下:

其中,u 和v 分别代表两个用户,N(u,v)的取值范围为[0,1]之间,值越小相似度越小;nu和nv分别为用户u 和v 的年龄。
(2)性别属性相似度,公式如下:

其中,u 和v 代表不同的用户,Xu和Xv分别是用户u 和v 的性别。
(3)根据上述用户性别和年龄属性相似度,根据实际情况分别给予不同的权重得出用户属性相似度,公式如下:
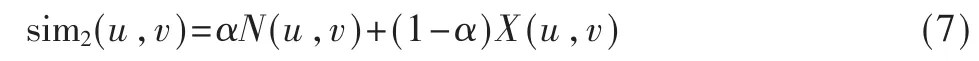
其中,权重系数α∈[0,1],在不同的推荐场景和领域中可以根据实际情况对α 值进行调整。
3 融合用户兴趣的协同过滤推荐算法
首先通过对sim1(u,v)和sim2(u,v)线性组合,将用户兴趣偏好和属性融合得到综合相似度,得到一种新的相似度计算模型,公式如下:
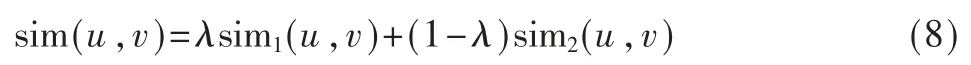
式中,λ∈[0,1]为权重系数,sim(u,v)值与两个用户的相似性成反比关系。
然后对项目进行评分预测,最后进行推荐,公式如下:
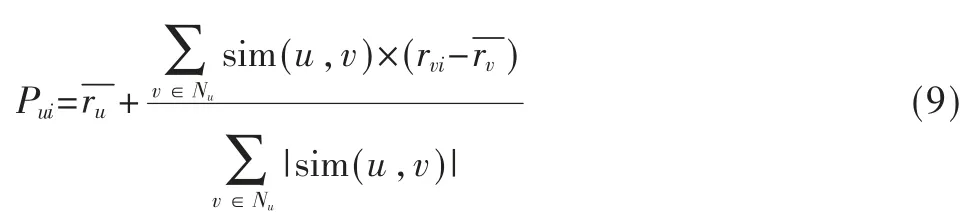
4 实验与分析
4.1 实验数据
实验采用开源的数据集MovieLens-1M。实验中使用交叉验证方式对用户评分进行预测。
4.2 评估指标
经过多轮训练减小评分误差,获得最优参数推荐模型。常用评价指标是平均绝对误差(MAE),这种误差计算方式见式(10):

其中,rui为用户u 对项目i 的真实评分,Pui为用户u 对于项目i 的预测评分。分母为测试集,分子为用户u 对项目i 真实评分和预测分数的差值。通过计算Test 中Pui与rui的平均绝对误差,评估模型的性能。
4.3 结果分析
首先确定本文涉及到的参数值,参数分别为:Ts、Tatt和λ。
实验1:通过MAE 值来确定时间窗口参数Ts的值。如图2 所示,在K=50 时,Tatt=20、Tatt=40、Tatt=60、Tatt=80、Tatt=100 的条件下,MAE 的值的变化趋势都是先降后升。当Tatt=40,Ts=4 时,MAE 值最小;当Tatt=100,Ts=5 时,MAE值最小;当Tatt分别为20、60 和80,Ts=6 时,MAE 值最小。令Ts=6 来进行后续的实验,即用户的兴趣偏好的变化周期为6 天。
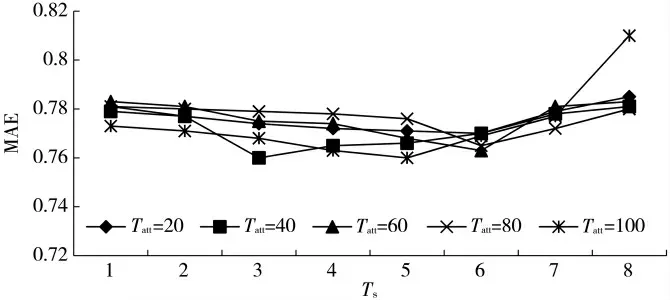
图2 不同Ts 值对应的MAE 值
实验2:判定Tatt的值。如图3 所示,在K=50,Ts=6时,Tatt=30、Tatt=40、Tatt=50、Tatt=60、Tatt=70、Tatt=80、Tatt=90时,MAE 的值先下降;到Tatt=60 时,MAE 值达到最低,然后上升。所以令Tatt=60,进行后续实验。
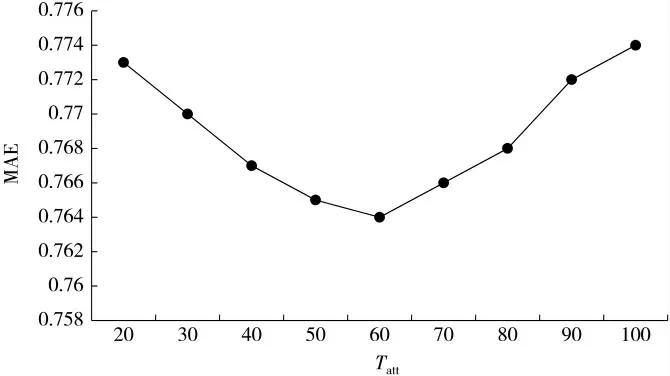
图3 不同Tatt 值对应的MAE
实验3:确定式(8)中参数λ 的值。当λ=1 时,sim(u,v)=sim1(u,v),表示只利用用户的兴趣偏好来计算用户之间的相似性;当λ=0 时,sim(u,v)=sim2(u,v),表示仅利用用户的属性计算用户之间的相似性。如图4 所示,在K=20、K=40、K=60、K=80 时,MAE 值先下降后上升;当λ=0.4 时,MAE 值最小,推荐效果最好。
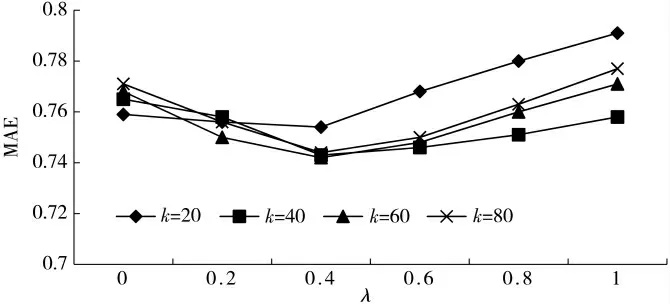
图4 不同λ 对应的MAE 值
实验4:在近邻不同的情况下,比较了不同推荐算法的推荐性能,其中包括将基于用户的协同过滤推荐算法(UBCF)[16]、基于K-means 聚类的协同过滤推荐算法(K-means UBCF)[17]、基于Canopy+K-means 混合聚类的协同过滤推荐算法(Canopy+K-means UBCF)与本文提出的算法进行了对比。得出的实验结果如图5 所示。

图5 不同算法对应的MAE 值
由图5 可知,随着目标用户最近邻居个数的增加,实验中所用的UBCF、K-means UBCF、Canopy+K-means UBCF 和本文所提出的算法的MAE 值都会逐渐降低并趋于一个稳定值。由图5 可以直观地发现,本文所提出的算法相对于其他3 种算法推荐准确度最高。例如,当最近邻居个数为35 时,Canopy+K-means UBCF 的MAE 值为0.758,同样条件下本文所提出的算法的MAE 值为0.741,推荐效果提升了1.7%。
5 结论
本文提出一种基于混合聚类与融合用户偏好的协同过滤推荐算法,通过建立Canopy+bi-Kmeans 混合聚类模型并且将传统的相似性度量算法中加入用户属性和用户兴趣偏好。实验结果表明,本文提出的基于混合聚类与融合用户偏好的协同过滤推荐算法在一定程度上提高了推荐可靠性。由于本文的算法是在各方面条件较为理想的环境下实现的,其鲁棒性和稳定性有待提高,因此下一步的工作是将该算法运用到现实项目中,并且不断追求更高的推荐效率。

