基于改进PSO的局部阴影下光伏阵列MPPT控制

张文异，王宏华

(河海大学 能源与电气学院，江苏 南京 211100)

0 引言

光伏阵列的输出特性具有非线性，并且其最大功率点容易受到光照强度和温度等因素的影响。为了提高光伏发电系统的发电效率，通过最大功率点跟踪(MPPT)控制使光伏阵列输出最大功率。然而在局部阴影的情况下，光伏阵列的P-V曲线会呈现多峰值的现象，传统算法如恒定电压法、扰动观测法、电导增量法等，存在陷入局部最优的问题。鉴于此，文献[1]提出一种将扰动观测法和差分进化法相结合的复合算法，虽然收敛速度较快，但其控制过于复杂，实用性不强。文献[2]提出一种变步长电导增量法，提高了动态响应速度，但容易陷入局部最优。

粒子群优化算法(PSO)作为一种全局寻优算法，适用于局部阴影下光伏系统的最大功率点跟踪。文献[3]提出惯性权重对数递减粒子群算法，虽然收敛速度较快，但仍然容易陷入局部最优。文献[4-5]提出变异粒子群算法，也没有改善容易陷入局部最优的问题。文献[6-8]改进传统的粒子群算法，不会陷入局部最优，但收敛速度较慢。本文在传统粒子群算法的基础上，通过自适应调节学习因子和惯性权重，来实现光伏系统在局部阴影下的最大功率点跟踪。

1 光伏阵列仿真分析

单块光伏电池等效电路如图1所示。图中，Iph为光生电流；Id为二极管中的暗电流；Rsh为等效旁路电阻，其阻值很大；Ish为旁路电流；Rs为等效串联电阻，阻值非常小；I为输出电流；R为负载；Uout为开路电压。

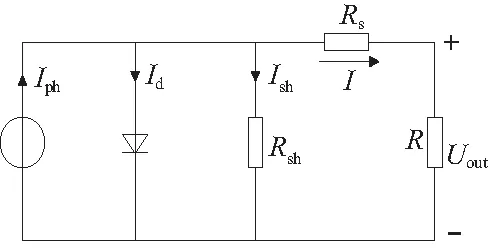
图1 光伏电池等效电路图

本文采用一种适合工程应用的近似仿真模型，根据厂商提供光伏阵列的相关参数对电池参数进行修正，得到如下公式：

ΔT=T-Tref

(1)

(2)

ΔU=-βΔT-RsΔI

(3)

I′=I+ΔI

(4)

U′=U+ΔU

(5)

式中：参考光照Sref=1 000W/m2；参考温度Tref=25℃；α=0.000 47Isc；β=0.003 2Voc。

光伏阵列由多个单块光伏电池串、并联组成，在参考情况下其输出特性可以简单看成单块电池输出特性的线性叠加。然而在实际情况中，光伏阵列会出现光照强度和温度不均的现象，因此光伏阵列的输出特性并不是简单的线性叠加。以下具体分析了光伏阵列分别在串联和并联条件下的输出特性。仿真采用的光伏阵列型号为TSM240，性能参数分别为：Pm=125W，Uoc=25.4V，Um=20.5V，Isc=6.52A，Im=6.12A，参考温度是25℃，参考光照为1 000W/m2。假设在局部阴影下，PV1的光照强度为1 000W/m2，PV2为700W/m2，PV3为500W/m2。

图2为3个光伏阵列相串联组成的光伏系统。

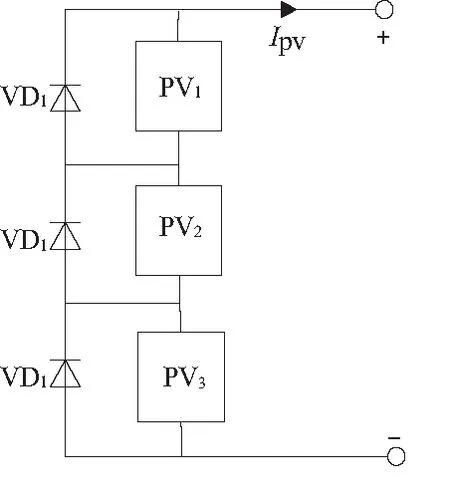
图2 三块光伏阵列串联

图3给出了串联阵列的I-V、P-V输出特性曲线。从图中可知，在局部阴影条件下串联型阵列的输出P-V曲线呈现多峰值特性。

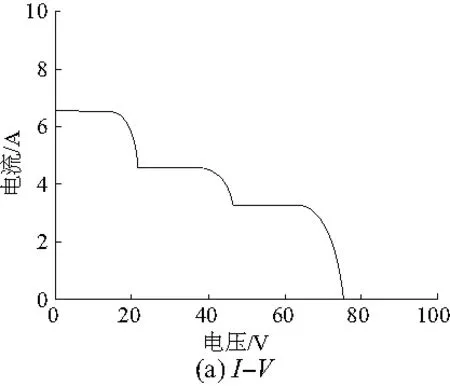
本文也研究了3个光伏阵列相并联组成的光伏系统。从仿真得知，在局部阴影条件下并联型阵列的输出P-V曲线呈现单峰值特性。

对串联型和并联型光伏阵列输出特性的仿真分析可进一步推广至串、并联共同组成的光伏阵列，假设光伏阵列为m×n，其中m为串联个数，n为并联个数，当光伏阵列的每条串联支路阴影情况均不相同时，最多会出现m个功率峰值点。

2 改进粒子群算法

粒子群优化算法作为一种全局寻优算法适用于多峰值寻优，因此经常被运用于局部阴影下最大功率点跟踪控制。其原理是首先初始化一群随机粒子，每个粒子都有各自的位置、速度和适应度，通过多次迭代最终得到每个粒子自己的最优解，简称为个体极值(Pbest)，并且在其中得到总体的最优解，简称为全局极值(Gbest)。粒子位置和速度的更新方程如下所示：

(6)

(7)

式中：i表示第i个粒子；k表示迭代次数；ω为惯性权重；c1和c2为学习因子；r1和r2为[0,1]上的随机数；x为粒子的位置；v为粒子的速度。

在粒子群优化算法中，惯性权重ω和学习因子c1、c2的取值会影响到算法的性能。ω取值过大全局搜索能力较强，ω取值过小局部搜索能力较强，初期设置较大的c1和较小的c2可以避免陷入局部最优，后期设置较小的c1和较大的c2可以收敛更快。因此，本文采用了一种自适应调节的方法，使惯性权重ω和学习因子c1和c2随着迭代次数k增加而更新，其公式如下所示：

(8)

(9)

(10)

式中：c1,beg、c2,beg是学习因子c1，c2的初始值；c1,end，c2,end是学习因子c1，c2的终止值；ωmax为惯性权重的最大值；ωmin为惯性权重的最小值；k为当前迭代次数；kmax为最大迭代次数。

粒子群优化算法应用在光伏阵列的最大功率点跟踪中时，一般没有设置迭代终止条件，但是如果一直让算法迭代下去，可能会造成在最大功率点附近振荡的现象。为了快速稳定在最大功率点上，设置了如下的迭代终止条件：粒子初始位置的标准差较大，收敛后的标准差就会变小，所以当粒子位置标准差小于设定的阈值时，则终止迭代，判定方程如下所示：

σ<δ

(11)

式中：σ为所有粒子位置的标准差；δ为设定的阈值。改进后的粒子群算法流程图如图4所示。

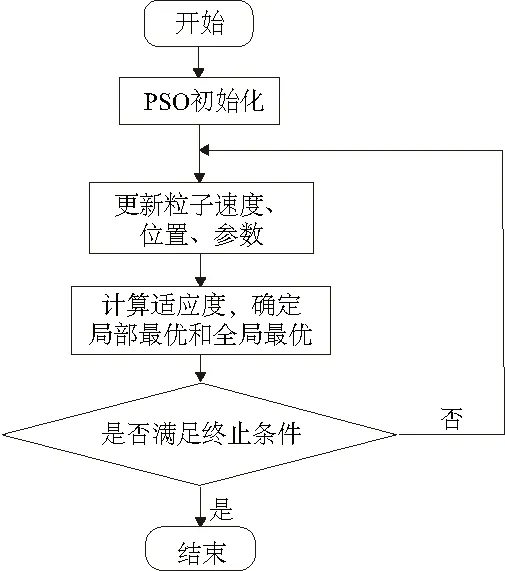
图4 改进PSO流程图

3 仿真验证

为验证改进的粒子群优化算法在光伏阵列的最大功率点跟踪控制中的正确性，本文在simulink中搭建了光伏系统，其中光伏系统由9块TSM240型光伏阵列串、并联组成。光伏阵列在标准条件下的额定功率Pm=125W，最大功率点电压Um=20.5V，最大功率点电流Im=6.12A，开路电压Uoc=25.4V，短路电流Isc=6.52A。参考情况下的光照为1000W/m2，温度为25℃。仿真时设置了两种局部阴影条件，条件一，9块光伏阵列的光照强度如下：PV1、PV4、PV7的光照强度为1000W/m2；PV2、PV5、PV8的光照强度为700W/m2；PV3、PV6、PV9的光照强度为500W/m2。光伏系统输出特性如图5所示。条件二，PV1、PV4、PV7、PV2、PV5、PV8光照强度均不变，而PV3、PV6、PV9的光照强度突变为200W/m2，其光伏系统输出特性如图6所示。

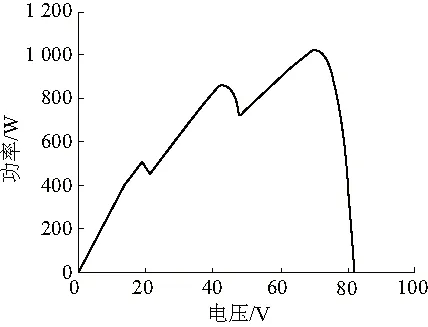
图5 条件一下输出特性

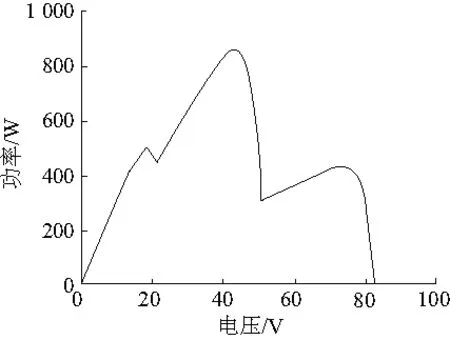
图6 条件二下输出特性

在MATLAB中仿真得到的功率和电压波形如图7-图10所示。在局部阴影条件一下改进粒子群优化算法在0.05s时追踪到了最大功率点Pm=1020W，Um=70.2V，功率波动范围在1 020～1 020.6W之间，电压波动范围在70～70.5V之间。

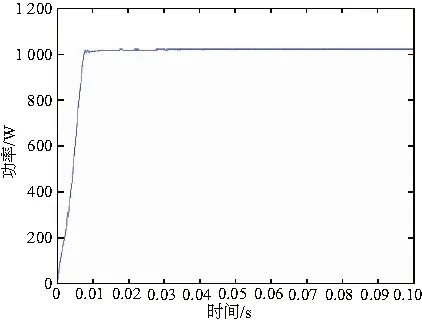
图7 条件一下功率波形

图8 条件一下电压波形

在局部阴影条件二下改进粒子群优化算法在0.06s时追踪到了最大功率点Pm=860.8W，Um=42.4V，功率波动范围在860.6～861.2W之间，电压波动范围在42～42.5V之间。

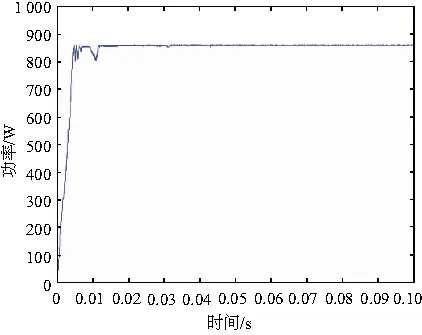
图9 条件二下功率波形

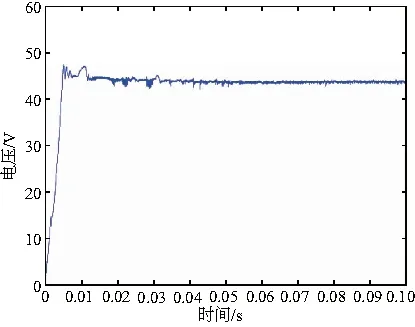
图10 条件二下电压波形

4 实验

本文进行了基于DSP数字控制系统软件和硬件设计，搭建了单级式光伏实验平台，并在平台上进行了改进粒子群优化算法的实验。由于外部环境没有达到参考光照和温度，故用光照仪和温度计测得当时的光照强度和温度如图11所示。用光伏模拟仪得到的开路电压Uoc为19.4V，Um为16.8V，模拟结果如图12所示。

在图11所示的外部环境下进行实验，实验结果如图13所示。从图13可知，通过MPPT得到的最大功率点电压为17.2V，与图12进行对比，表明了改进的粒子群优化算法在最大功率点跟踪控制中的正确性。

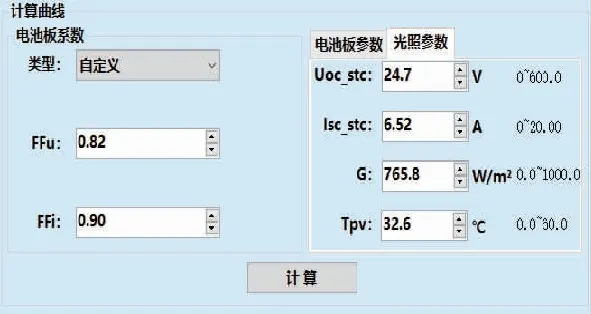
图11 实际环境参数

图12 模拟输出特性

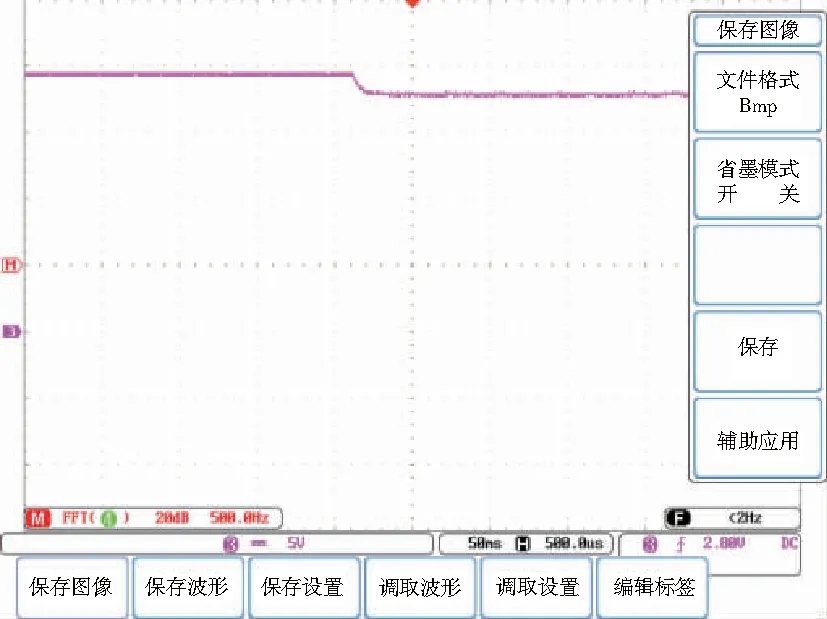
图13 改进PSO的MPPT实验结果

5 结语

本文研究了一种改进的粒子群优化算法，改进后的粒子群优化算法克服了传统粒子群算法容易陷入局部最优的缺点，同时收敛速度较快，并且通过两种不同阴影条件下仿真表明：经过改进的粒子群优化算法，在局部阴影下能够实现最大功率点跟踪，有较强的实用性。