基于压缩感知的可视化环境监测系统研究

张骞，裴荣，徐昕，胡妤

(南京理工大学 机械工程学院，江苏 南京 210094)

0 引言

在信息技术迅猛发展的时代背景下，信息量爆炸式增长，人们也迫切地需要感知更为丰富的环境信息(图像、声音、视频等)来实现细粒度、更直观的可视化环境监测[1-2]。

传统图像监测系统一般采用有线的方式来完成，有线方式不仅会浪费大量的人力和财力，同时，架设的线路管道很有可能破坏监测区域生态环境。在无线传感器网络中，传统的信号采样方式采用的是奈奎斯特采样定理，该定理规定采样速率不得低于信号带宽的两倍。传统的采样定理虽然能够高精度重构信号，但是给硬件设备的数模转换器和数字处理器带来了巨大负担。同时，大量的数据采集会加速损耗节点的能量，不符合无线传感器网络的低功耗设计要求。

从2006年开始，CANDES E J、DONOHO D L和TAO T等提出了一种不同于奈奎斯特采样定理的新型采样理论，即压缩感知理论[3-5]。该理论指出：如果某个信号本身是稀疏的或在某个稀疏表示基矩阵上能够进行稀疏化表示，那么该信号就可以通过一个与该稀疏表示基矩阵不相关的测量矩阵将高维信号投影到低维空间中进行测量，得到的测量值仅保留少量的有效元素，最后通过重构算法重构原始信号。压缩感知采样方式采用亚采样方式，它打破了等间距采样方式的局限性，具有减少数据冗余，节省存储空间的特点，可以有效地降低网络拥塞，延长网络使用寿命。本文将压缩感知技术与无线传感器网络相结合，实现图像的采集、无线传输与重构，有效降低了数据存储和网络传输的负担。

1 压缩感知理论

相较于传统的采样定理，压缩感知技术将数据采样和压缩同时实现，以低速率进行随机亚采样，减少数据冗余，以低维观测取代高维数据，并以较少的测量值近似重构原始信号[6]。压缩感知理论的研究内容主要包括三个方面：信号的稀疏化表示、压缩感知测量矩阵和信号的重构算法。

1.1 信号的稀疏化表示

信号的稀疏化表示是将信号投影到某个稀疏表示基矩阵上，用少量非零元素简洁地表达原始信号[7]。

从数学的角度来讲，对于一个长度为N的一维原始信号x在稀疏基矩阵Ψ进行稀疏化表示，其稀疏化过程可以简化为下述数学公式：

(1)

其中：Ψ为一个N×N维的稀疏基矩阵；S为N×1维的列向量，称为稀疏系数。

在图像处理领域最常用的是非冗余变换基，如：离散小波变换基、离散傅里叶变换基、离散余弦变换基等。其中，小波的多分辨分析能力可以很好地描述图像的整体特征和局部分析，应用较为广泛，所以本文采用离散小波变换对原始图像进行稀疏化处理。

1.2 压缩感知测量矩阵

测量矩阵是将高维数据投影到低维空间中，得到的测量值y远少于原始信号的数据量，其投影过程如下述公式所示。

y=ΦΨS=ΘS

(2)

式中：y为测量值，是一个长度为M的一维列向量；测量矩阵Φ是M×N维的矩阵，其中M≪N；Ψ是N×N维的稀疏基矩阵；S是稀疏系数，是原始信号x的稀疏化表示；令Θ=ΦΨ，Θ为M×N维的矩阵，称为传感矩阵。

为了判断某个矩阵是否可以作为压缩感知测量矩阵，TAO T、CANDES E J等人提出：测量矩阵Φ应满足约束等距性条件(restricted isometry property)，简称RIP[8]。RIP准则具体描述如下：

(3)

对于任意常数，若存在δk∈(0,1)满足式(3)，则说明测量矩阵Φ满足RIP准则。

常用的测量矩阵有：随机高斯矩阵、随机伯努利矩阵、部分哈达玛矩阵、确定性矩阵等。其中部分哈达玛矩阵相比于其他测量矩阵，结构简单，易于硬件实现，只需少量的测量值就能够高精度恢复原始信号，所以本文选择部分哈达玛矩阵作为图像信号的测量矩阵。

1.3 信号的重构算法

信号重构的过程是将稀疏度为K的信号x从M维的测量值y中精确地恢复出来，是压缩采样的逆过程[9]。

首先定义一个向量α={α1,α2,α3…,αN}的p-范数，来描述信号重构的过程，其定义如下：

(4)

其中若p为0，则表示为l0范数，表示向量α中非零元素的个数。信号的重构就可以转化成通过l0范数求解最优化问题：

(5)

(6)

转化式(6)，得

(7)

对于稀疏度为K的稀疏信号x∈RN，若要得到l1范数的最优解，则测量值y的个数M必须满足以下不等式：

M≥C·μ2(Φ,Ψ)·K·logN

(8)

由式(8)不难看出，测量值的个数M与稀疏度K、相关性μ(Φ,Ψ)的大小呈正相关。稀疏度K越小，测量矩阵与稀疏基的相关性μ(Φ,Ψ)越低，重构信号所需的测量值的个数M就越少，而重构效果也就越好。

2 监测系统设计

2.1 系统总体设计

系统主要包括三个部分：传感节点、汇聚节点和上位机，系统设计的总体架构如图1所示。

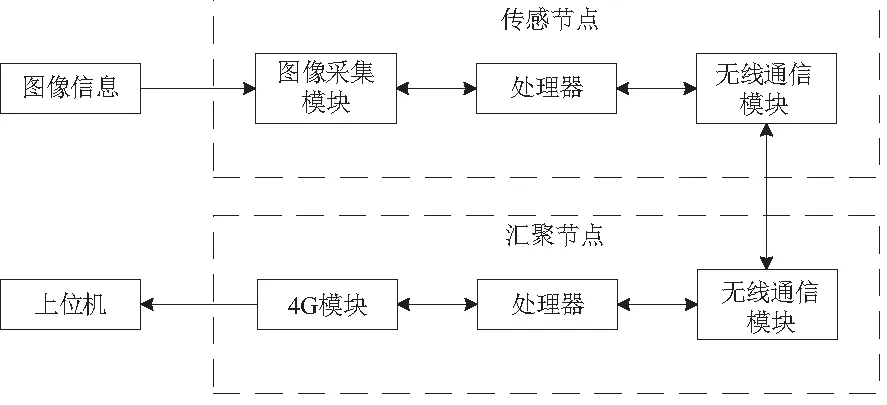
图1 系统设计总体架构

监测系统中，传感节点是压缩感知采样的硬件实现基础，节点以STM32F407芯片作为节点的主控芯片，并增加OV5640图像采集模块、nRF24L01无线通信模块以及HC-SR501红外感应模块等外围模块，实现图像信号的采集和处理，其传感节点设计框图如图2所示。

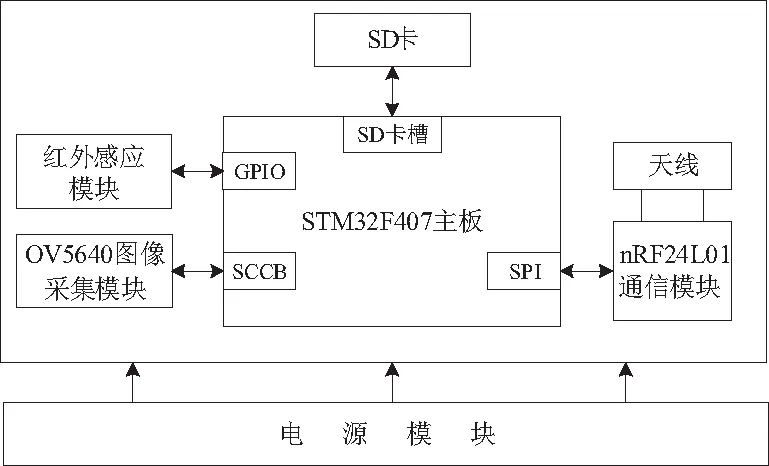
图2 传感节点设计框图

红外感应模块保证了传感节点的低功耗运行，通过与STM32自带AD采样功能监测红外感应模块的电平输出情况，实现传感节点的主动触发图像采集功能。

汇聚节点主要负责对图像数据和传感节点信息的打包处理及通过协议转换上传至云服务器。nRF24L01无线通信模块负责接收各通道的图像数据，并保存在SD卡。M750 4G模块通过串口方式读取图像数据，将数据传至云服务器，其设计框图如图3所示。

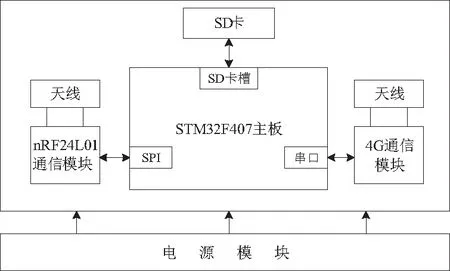
图3 汇聚节点设计框图

上位机接收到云服务器的数据，对图像数据进行重构，还原图像信号并显示，完成可视化环境监测。上位机运行的重构算法选取正交匹配追踪算法(OMP)，利用LabVIEW软件中的MATLAB script模块实现重构算法的编写，如图4所示。

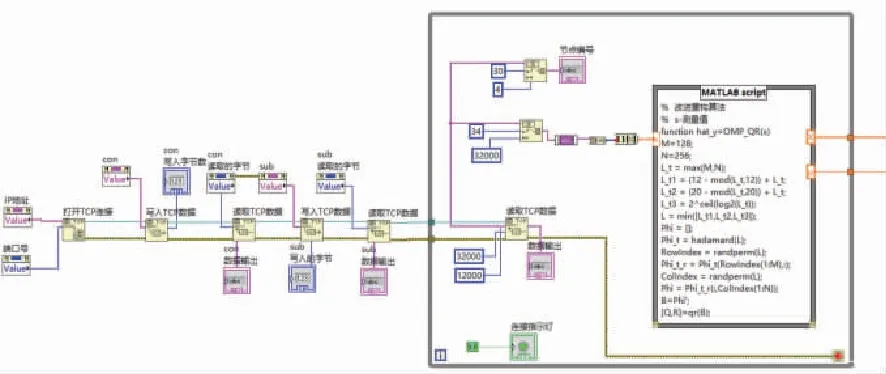
图4 上位机的重构算法实现

2.2 压缩感知算法实现

由于传感节点的处理能力有限，运行在传感节点的压缩感知算法包括图像的稀疏化处理和测量矩阵的测量，即图像压缩处理。实现流程如图5所示，具体实现步骤如下：

1)图像采集模块初始化设置，对监测区域进行图像采集；

2)对图像矩阵进行离散小波变换：通过离散小波算法对图像矩阵进行滤波处理，得到1个低频子带XLL和3个携带高频分量的子带XHH、XHL、XLH，将高频子带保存到数组中；然后再次对低频子带XLL进行离散小波变换；以此类推，为了更好地重构原始图像，设定最大分解层数为8，分解得到的子带矩阵按一定顺序存入到二维数组中，组成一个N×N维矩阵；

3)利用测量矩阵对子带矩阵进行测量，得到图像的测量值y；

4)将得到的测量值临时保存在SD卡中，通过无线传输模块传输至汇聚节点。

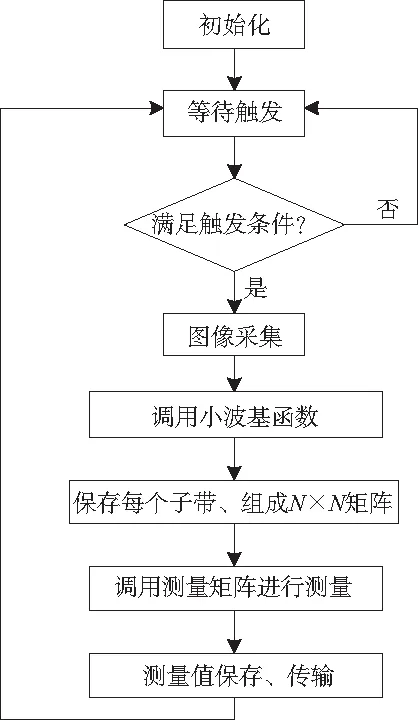
图5 压缩感知算法实现流程图

3 可视化监测系统性能验证

3.1 系统的可行性验证

对系统进行可行性验证时，不易将系统放置在噪声较大的实际环境中，所以将系统放置在室内环境进行可行性验证，实物图如图6所示，放置地点如图7所示。

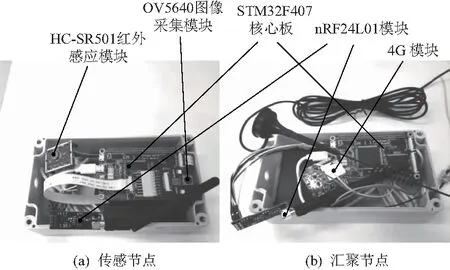
图6 传感节点和汇聚节点实物图

图7 节点布置示意图

实验的测量率设定为0.5，图像输出格式设定为256×256大小的灰度图。各节点重构效果如图8、图9、图10所示，重构图像的PSNR值如表1所示。

图8 节点1重构效果图

图9 节点2重构效果图

图10 节点3重构效果图

表1 各传感节点重构图像的PSNR值 单位：dB

由实验结果可得：测量率为0.5时，系统在室内环境中运行稳定，重构图像的PSNR值较高。重构图像的轮廓可以反映原始图像信息，细节部分需要进一步处理，重构质量可以达到预期效果。

3.2 系统在实际环境中的性能验证

由3.1小节可知，监测系统可以在室内环境下实现图像采集、传输和重构的功能，为了进一步验证系统实际运行的稳定性和功能性，将监测系统放置在实际环境中进行测试，并增加传感节点，测试环境如图11所示，节点布置示意图如图12所示。

图11 实际环境节点布置情况

图12 节点布置示意图

考虑到实际环境中干扰因素较多，在实际传输过程中可能出现丢包现象，所以将测量率设定为0.7，各节点重构效果如图13-图18所示，重构图像的PSNR值如表2所示。

图13 节点1重构效果图(测量率为0.7)

图14 节点2重构效果图(测量率为0.7)

图15 节点3重构效果图(测量率为0.7)

图16 节点4重构效果图(测量率为0.7)

图17 节点5重构效果图(测量率为0.7)

图18 节点6重构效果图(测量率为0.7)

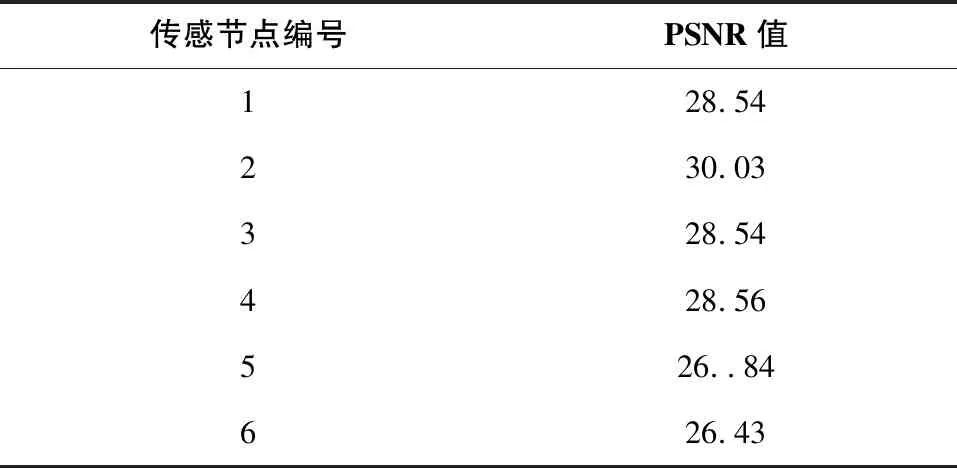
表2 各传感节点重构图像的PSNR值 单位：dB (测量率为0.7)

由实验结果可得：系统在实际环境中运行时，干扰因素较多，实际运行性能不如室内环境，部分节点出现了丢包现象，导致重构图像质量不高。但是，在测量率为0.7时，各个节点运行较为稳定，采集到的图像数据可以在上位机近似重构，重构图像的PSNR值约在28dB～30dB，重构效果较好，满足可视化环境监测系统的设计要求。