基于动力学的协作机械臂零力拖动研究

刘镔震，潘松峰，李先弘，王先月，伊永祺

(青岛大学 自动化学院，山东 青岛 266000)

0 引言

随着机械臂产业的发展及用人成本的上升，我国制造业向着智能化、无人化的方向快速发展。由于协作机械臂具有一定人机交互能力，因此其不仅出现在商场等民用领域，更在军用、医疗等领域有了突飞猛进的发展。零力拖动，即由操作员直接拖动机器人各关节运动至理想位姿并进行记录。作为协作机械臂与操作者共同工作的一种协作方案，具有重要的研究意义。

针对某公司一种基于开环力矩控制方法的6轴协作机械臂开发平台进行机械臂本体动力学分析，并结合电机模型对机器人进行关于零力拖动的相关研究，利用实验对摩擦补偿参数等进行校准，确保机械臂可在工作范围内实现零力拖动。机械臂本体及相关尺寸数据如图1所示。

图1 机械臂本体及相关尺寸图

1 动力学建模

采用改进D-H参数法对6自由度协作机械臂进行建模，其机械臂结构原理如图2所示，D-H参数如表1所示。

由于机器人从关节4之后杆长均为0，因此仅对协作机械臂的前3个关节进行研究。

机械臂动力学的机器人本体动力学研究常见有Lagrange法[1-3]、Newton-Euler法[4-6]和Dalembert法[7-8]等。为了便于计算及具象化研究，本文采用Lagrange法进行动力学建模与分析。

图2 6自由度机械臂结构原理图

表1 D-H参数表

Lagrange法的数学模型如式(1)所示。

L=K-P

(1)

式中：L为Lagrange函数；K为机械臂本体系统动能；P为系统位能。在此基础上动力学方程可表示为[9]

(2)

结合式(1)、式(2)，机械臂的本体动力学也可以写作式(3)形式：

(3)

将式(3)中的哥氏力和离心力分离，机械臂的本体动力学也可写作式(4)形式：

(4)

式中C(q)和F(q)均为3×3的矩阵。

系统位能考虑惯性带来的势能，因此采用转动惯量法计算力矩。机械臂的质量分布在伺服电机及连杆上，产生绕中心轴线旋转(伺服电机)和绕远端关节旋转(连杆)两种转动惯量，如图3(a)、图3(b)所示，参数示意图如图3(c)所示。

图3 转动惯量及机械臂参数示意图

中心轴线转动惯量由伺服电机形成，即Jm1、Jm3和Jm5，计算方式如式(5)所示；远端关节转动惯量由连杆形成，即Jm2、Jm4和Jm6，计算方式如式(6)所示。

(5)

(6)

其中各字符含义如图3(a)、图3(b)所示。图3(c)中：l2表示关节1电机和关节2电机之间，连杆质心与电机1质心之间的距离；l3表示关节1电机和关节2电机之间，连杆质心与关节2电机之间的距离；关节1和关节2之间距离很短，此处忽略，从而得到机械臂动力学所需转动惯量的物理参数。

由此建立起机械臂本体的动力学模型，其动力学方程中的具体参数为：

m6l3l6)c2-2m6l5l6c3-2m6l3l6c23，

(m4l3l4+m5l3l5+m6l3l5)c2-2m6l5l6cosθ3-m6l3l6c23，

c11=0,

c12=-(m4l3l4+m5l3l5+m6l3l5)s2+m6l3l6s23，

c13=m6l5l6s3+m6l3l6s23，

g1=[m2l2+m3l3+(m4+m5+m6)l3]gc1+(m4l4+m5l5+m6l5)gc12+m6gl6c123。

推导结果较为复杂且篇幅有限，不再赘述。此处本体动力学模型处于理想状态下，而在实际模型中电机除输出式(4)所得力矩外，还需考虑库仑摩擦力矩τf及黏性摩擦力矩τg，其计算方式如式(7)、式(8)所示。

(7)

τg=N·sign(q)

(8)

式中：M为黏滞系数矩阵；N为库仑力向量；q为关节输出角度而非电机输出角度。将式(7)、式(8)代入式(4)中，并加入机械臂各轴电机的减速比，得到各轴电机的理论输出力矩如式(9)所示。

(9)

(10)

式中ri表示第i个关节电机的减速比，由电机固件决定。通过关节电机减速比矩阵T将关节力矩与电机实际输出力矩结合。

2 电机模型

电机是机械臂关节力矩的提供者，因此需要将电机模型与零力模型相结合。本文采用永磁同步电机PMSM，数学模型如式(11)所示[10]。

(11)

式中：ud、uq分别为永磁同步电机d轴和q轴定子的电压；id、iq分别为永磁同步电机d轴和q轴定子的电流；ω为转子角速度；Φ为电机永磁体磁链；J为转动惯量；TL为电机负载转矩；Te为电磁转矩。由于在式(9)中已从能量观点对转动惯量进行运算，电机侧不需再对转动惯量进行单独运算。

以单关节电机为例对电机模型进行研究。如图4所示，机械臂关节属于多轴传动系统，电机与关节之间由减速器连接，ωS为电机侧转子转速，qdi为电机输出角度，ωL为关节侧转速，qi为关节实际输出角度，四者关系如式(12)所示。

(12)

图4 电机传动示意图

(13)

(14)

其结构图如图5所示，实现闭环控制方案。

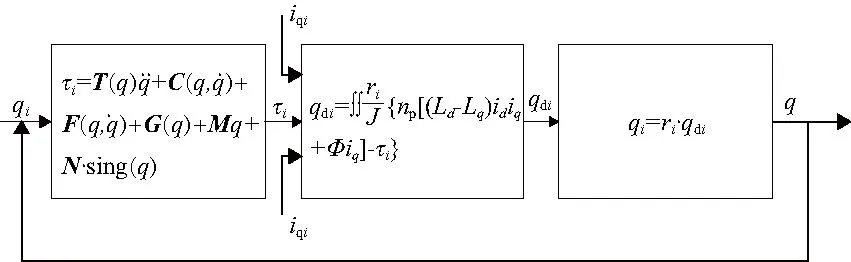
图5 零力拖动模型结构图

3 零力控制模型

零力控制模型就是将考虑各类摩擦及惯性力的机器人本体动力学方程与电机模型结合得到的包含式(9)和式(14)的综合模型，人为拖动过程力矩模型如式(15)所示。

(15)

式中P为力矩矩阵，其表达式为

(16)

4 实验与分析

利用6轴协作机械臂开发平台所自带的运动传感器及动力学参数识别，以第2关节为例进行相关实验。其实验验证图如图6所示，J2(2)为库仑摩擦系数，对应式(15)中的N，J2(3)为黏性摩擦系数，对应式(15)中的M。

图6 单关节零力拖动验证图

首先将模型拷入电机控制卡并对其参数进行预设。预设M=N=10，图6中J2(4)为动力学补偿参数，应为1。预设参数的目的在于避免机械臂在零力状态下因重力导致限位，保证其安全性。随后通过对库仑摩擦力矩和黏性摩擦力矩补偿，得到M和N的最优值，确保机械臂可进行零力拖动。找到最优值的方法为：当所给定M和N过小时，会因补偿不足无法实现零力拖动；当所给定M和N过大时，可实现零力拖动，但会因补偿过度导致卡死或拖动困难。机械臂厂商在只补偿重力、库仑摩擦力和黏性摩擦力的情况下给定M的最优值为25，N的最优值为42。最后通过比对M和N的方式验证模型准确性。

通过验证可知，当库仑摩擦参数M>15、黏性摩擦参数N>30时有较好的零力拖动效果。在此条件下通过人为拖动机械臂，转动第二关节使其关节角从0°拖动至30°位置，得到库仑摩擦力矩、黏性摩擦力矩、动力学力矩与时间关系如图7所示。

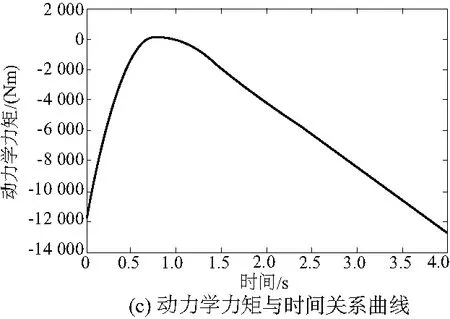
图7 库仑摩擦力矩、黏性摩擦力矩、动力学力矩与时间关系图

由于零力拖动需人为进行操作，因此图7中黏性摩擦力矩在1.5s后呈现出抖动现象为人为操作影响。通过验证，当库仑摩擦参数M=20、黏性摩擦参数N=40时达到机械臂零力拖动的最佳状态。二者均小于厂商所给定的数值。原因是由于厂商给定M和N时并未对其他惯性力等补偿，只能通过增大库仑摩擦力矩和黏性摩擦力矩间接补偿其他惯性力。由此证明模型的准确性，并为零力拖动准确控制提供了依据。

5 结语

针对一种6自由度协作机械臂，利用动力学方程、静力学原理及电机转动轴参数关系对零力拖动进行研究。通过实验平台验证的方法对模型参数进行补偿，当库仑摩擦参数M=20、黏性摩擦参数N=40时准确地实现了机械臂的零力拖动控制，证明了模型的准确性。此模型较于传统的重力补偿零力拖动控制而言，采用动力学及摩擦力补偿方式从电机角度实现了零力拖动的准确控制，解决了控制精度不足的问题，也为日后研究工业协作机械臂的动力学控制夯实了基础。