基于图谱特征与度量学习的行星齿轮箱健康评估

李加兴，陈广艳，张鲁晋，王友仁，张砦

(1. 南京航空航天大学 自动化学院，江苏 南京 211106；2. 中国航发湖南动力机械研究所 直升机传动技术国防科技重点实验室，湖南 株洲 412000)

0 引言

行星齿轮箱具有较大的传动比与承载能力，广泛应用于直升机主减速器、风电机组等机械装置。由于行星齿轮箱运行在高速与重载的情况下，其关键零部件极易发生故障，开展行星齿轮箱在线监测与健康评估研究具有重要的意义[1]。

故障特征参数提取作为健康评估中的关键环节，特征参数的好坏直接决定健康评估结果。张龙等[2]将时域和频域特征组合成多域特征矢量，建立基准高斯混合模型(GMM)，以多域对数似然概率作为健康指标，实现滚动轴承性能退化评估。对振动信号进行时域或频域分析，提取相应统计特征，是目前最常用的特征参数提取方法。然而由于行星齿轮箱振动信号具有非线性、非平稳性，且传统的特征提取方法需要大量的信号处理知识和丰富的专业经验，故提取有效的故障特征参数比较困难。

度量学习(metric learning，ML)是从训练数据中学习一个度量函数，用于计算样本间的相似度或距离。作为度量学习最常用的度量函数，马氏距离可以很好地度量样本间的距离。赵帅等[3]提取时域与频域特征并降维，计算降维特征与基线数据的马氏距离，以马氏距离对数作为健康值用于反映滚珠丝杠健康状态。乔美英等[4]采用在线度量学习模型对马氏度量矩阵进行学习，提高了分类准确率和鲁棒性。目前度量学习大多用于数据分类与故障检测，在健康评估中应用较少。

RAI A等[5]提出基于自组织映射-最小量化误差演化的滚动轴承性能退化指标，并采用轴承健康指数构建支持向量回归模型对轴承进行寿命估计。张云超等[6]建立齿轮裂纹扩展有限元模型，对齿轮进行寿命估计。ZHANG J等[7]研究了风力发电机健康评估方法，采用高斯混合模型对正常数据建立健康基线，并采用马氏距离计算当前状态与健康基线的距离进行健康评估。但以上健康评估方法中健康指标(health indicator, HI)在退化过程中波动较大、单调性较差，使得健康评估存在较大误差。

为了提高健康指标与故障严重程度之间的单调性与相关性，提高健康评估准确性，本文提出一种基于图谱特征与度量学习相结合的行星齿轮箱健康评估方法。首先对行星齿轮箱振动信号提取图谱特征；利用度量学习构建马氏距离度量函数，并结合支持向量回归模型实现行星齿轮箱健康评估。

1 图谱特征参数提取

1.1 路图信号

路图定义为一个顶点与顶点由边依次连接的序列。行星齿轮箱离散振动信号与路图信号的转换关系为：振动信号的采样点对应路图的顶点，振动信号的幅值对应路图信号序列[8]。因此，路图顶点vi与振动信号值xi(i=1,2,…,n)相对应，xi表示顶点vi的值，则与振动信号对应的路图信号可表示为

X=[x1,x2,…,xn]T

(1)

1.2 图谱特征参数

图谱指标是图矩阵特征值的函数，而最常用的图矩阵有邻接矩阵W和拉普拉斯矩阵L。邻接矩阵W中每个元素wij为连接两个顶点vi与vj边的权值。若两个顶点之间没有边连接，则wij=0。wij通常人为设定，与顶点值xi、xj有关，本文取

(2)

拉普拉斯矩阵L定义为

L=D-W

(3)

式中D为度对角矩阵，其对角元素为di=∑wij。

根据式(4)计算W和L的特征值和特征向量

Wzi=λizi
Lyi=μiyi

(4)

式中：λi、zi为邻接矩阵W的特征值和特征向量；μi、yi为拉普拉斯矩阵L的特征值和特征向量。

本文提取的图谱特征如表1所示。

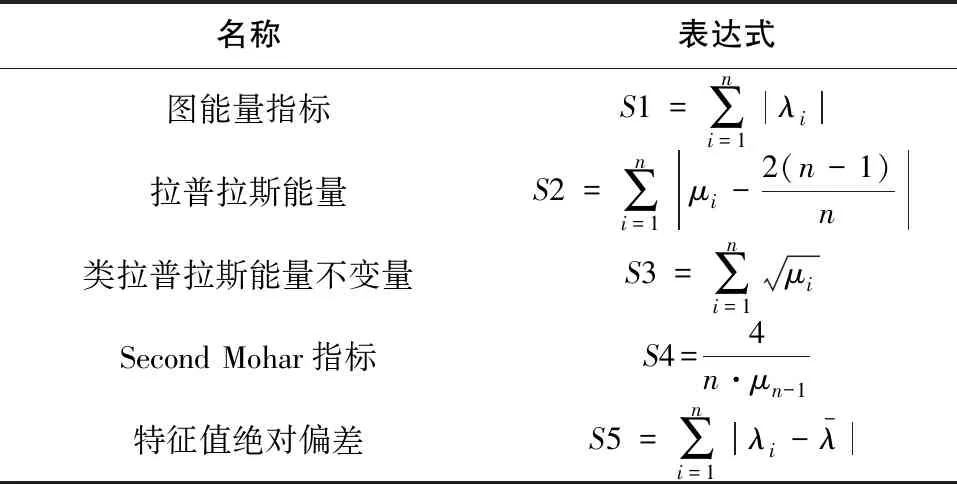
表1 图谱特征

2 马氏距离度量学习

2.1 马氏距离

马氏距离是由印度统计学家Mahalanobis提出的，可以有效计算两个样本的相似度。样本x1、x2之间的马氏距离可表示为

(5)

式中C为协方差矩阵。

采用单调性与相关性对马氏距离进行评价，其表达式如式(11)和式(12)所示。

(6)

(7)

式中：N为马氏距离d的数据长度；k表示故障严重程度。

单调性和相关性值始终处于[0,1]，越趋于1，表明马氏距离越符合期望要求。将单调性和相关性加权平均，作为综合评分JM，即

JM=0.5Mon+0.5Corr

(8)

2.2 度量学习

为了提升马氏距离的单调性与相关性，引入度量学习(metric learning，ML)对马氏矩阵M进行学习。将公式(5)改写成如下形式

(9)

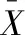
根据度量学习模型，对马氏矩阵进行学习，即：

(10)

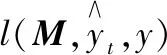
(11)

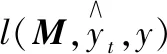
(12)

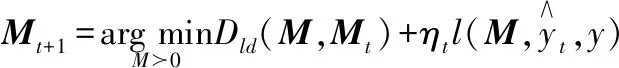
(13)

为了保证马氏矩阵M的半正定性，ηt需要满足

(14)

因此，马氏矩阵度量学习过程如下：

输入：正常状态特征X，不同故障阶段的特征Y。

a)归一化X、Y；

b)设置初始马氏矩阵M1=I，迭代次数N，期望损失误差ρ；

c)Fort=1, 2,…,N；

1)使用Mt计算Y与X之间的马氏距离d；

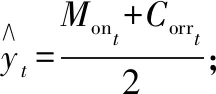
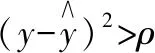
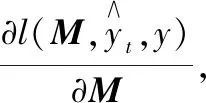
5)更新M，

6)若t=N，则退出循环，否则返回步骤c)。

输出：马氏矩阵M。

3 健康评估方法

3.1 基于支持向量回归的健康评估模型

设训练样本

D=[(x1,y1),(x2,y2),…,(xm,ym)}]

(15)

式中：xi∈Rn；yi∈R；x为输入样本；y为输出样本。支持向量回归函数表达式为

f(x)=ωφ(x)+b

(16)

式中：ω为权重向量；b为偏置；φ(x)为非线性映射，可以将样本点映射到高维空间。对于参数ω和b，通过求解最小值优化问题获得：

(17)

(18)

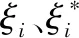
通过求解上述模型的拉格朗日方程对偶问题获得最优解，得到回归模型

(19)

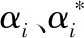
3.2 行星齿轮箱健康评估实现

基于马氏距离度量学习与支持向量回归(MDML-SVR)的行星齿轮箱健康评估方法实现流程如图1所示。

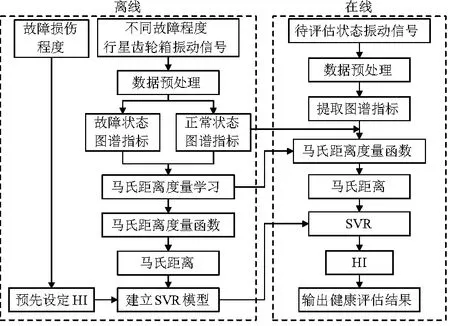
图1 基于MDML-SVR的行星齿轮箱健康评估方法

4 实验及结果分析

4.1 实验方案

采用的行星齿轮箱故障模拟实验平台如图2所示。该实验平台主要由变速驱动电机、平行齿轮箱、行星齿轮箱与磁粉制动器组成。实验设置了共195种工况：15种转速600～2 000r/min，13种负载0～27N·m。在太阳轮上植入了4种不同尺寸的点蚀故障，记为ds1-ds4，无故障正常状态记为ds0，如图3所示。4种点蚀直径均为2mm，点蚀深度及数量见表2。根据点蚀故障面积及深度，设定故障严重程度分别为20%、40%、60%、80%。数据采集时采样频率为40 960Hz，采样时间为25.6s。

图2 行星齿轮箱故障模拟实验平台

图3 太阳轮点蚀故障

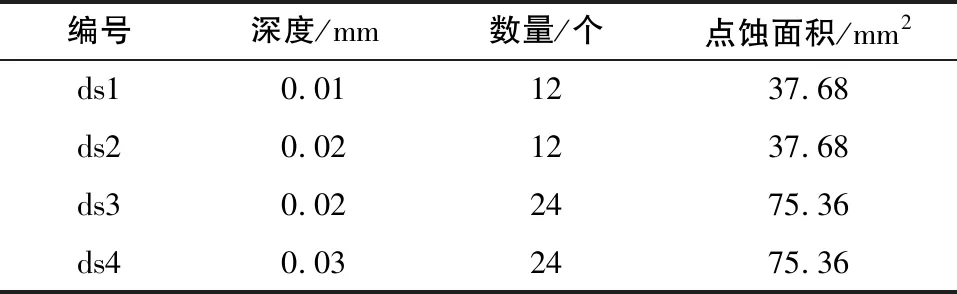
表2 太阳轮点蚀故障尺寸

4.2 振动信号特征参数

选用转速为600r/min、载荷为6.75N·m工况下水平方向的振动信号并进行小波降噪处理，分别提取图谱特征S1-S5。为了对比分析，提取常用的时域特征参数均方根、峰值、峭度、裕度因子，频域特征参数平均频率、频率标准差。

对图谱特征、时频、频域特征分别计算其随故障严重程度变化的单调性、相关性与综合评分，具体评分值见图4。

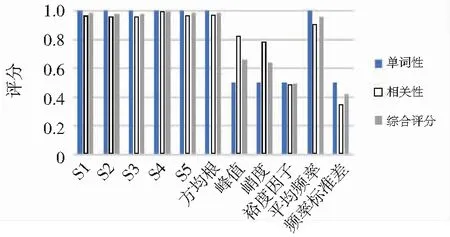
图4 特征参数评分

图谱指标的综合评分普遍高于时域、频域特征，均在0.97以上。方均根作为最常用的时域特征，其综合评分为0.985 2，低于图谱指标S4的0.994 7。以上分析表明图谱指标在表征故障严重程度方面优于常用的时域与频域特征。

4.3 不同健康评估方法结果比较

在每种故障程度下，取前25s振动信号，并平均分为25组，每组分别提取图谱指标S1-S5，组成25×5的特征参数集。从25组特征参数中随机选择20组作为马氏矩阵度量学习训练数据，其余5组作为测试数据。根据度量学习步骤，设定初始马氏矩阵为单位矩阵，对马氏矩阵M进行训练，从而得到马氏距离度量函数。

采用协方差矩阵C与度量学习的马氏矩阵M分别计算5组测试数据中不同故障严重程度特征参数与基准特征向量的马氏距离，并归一化处理，分别记为MD、MD-ML，如图5所示。

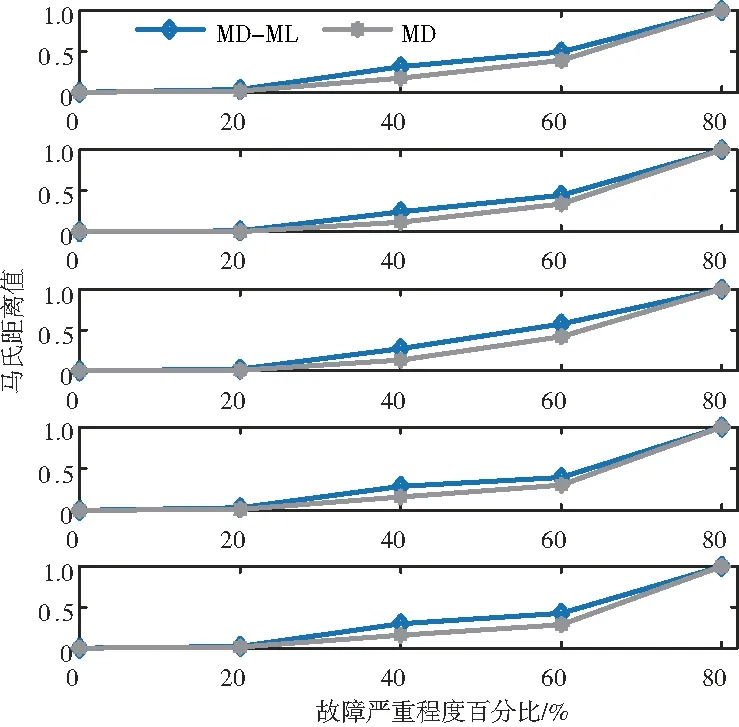
图5 不同故障严重程度下的马氏距离

从图5可以看出两种方法计算的马氏距离均随着故障严重程度单调递增。为了更准确地比较度量学习对马氏距离提升效果，采用单调性、相关性对马氏距离进行评价，并计算综合评分，如图6所示。经过度量学习后，马氏距离相关性分别提高了5.01%、5.99%、5.99%、5.49%、7.40%，综合评分分别提高了2.38%、2.80%、2.80%、2.57%、3.45%。

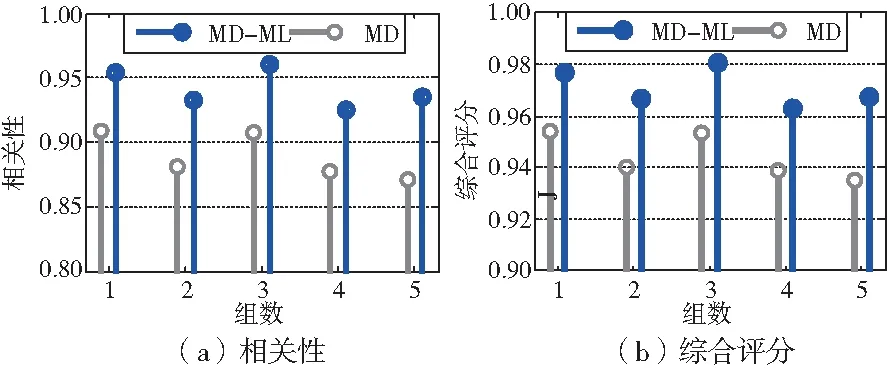
图6 度量学习评分对比

为了对比本文方法的有效性，采取未度量学习的马氏距离函数MD-SVR、欧氏距离函数ED-SVR以及GMM-SVR、MDML-Logistic方法进行分析。

根据太阳轮点蚀损伤程度预先设定健康指标，正常状态ds0时HI=1，ds1-ds4时，HI分别为0.8、0.6、0.4、0.2。分析与图7中度量学习前后健康评估结果可以发现，采用本文方法得到的HI更贴合实际结果，随故障加深而减小，且不同健康状态区分明显，符合预期结果。其他方法在正常状态ds0与ds1时的评估结果非常接近，不足以区分健康状态。ED-SVR与GMM-SVR在ds1的HI大于正常状态ds0的HI，不符合实际结果。

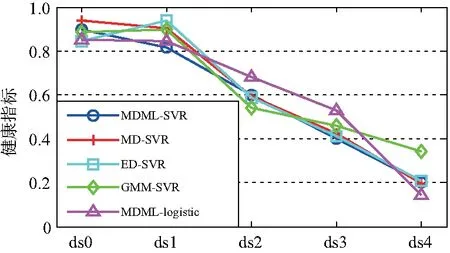
图7 健康评估结果比较

为了准确、全面地比较健康评估结果，对HI随故障程度变化曲线进行评价，如表3所示。MDML-SVR方法的相关性与综合评分最高，分别为0.991 2与0.995 6，其次是MD-SVR、MDML-Logistic，ED-SVR、GMM-SVR最低。

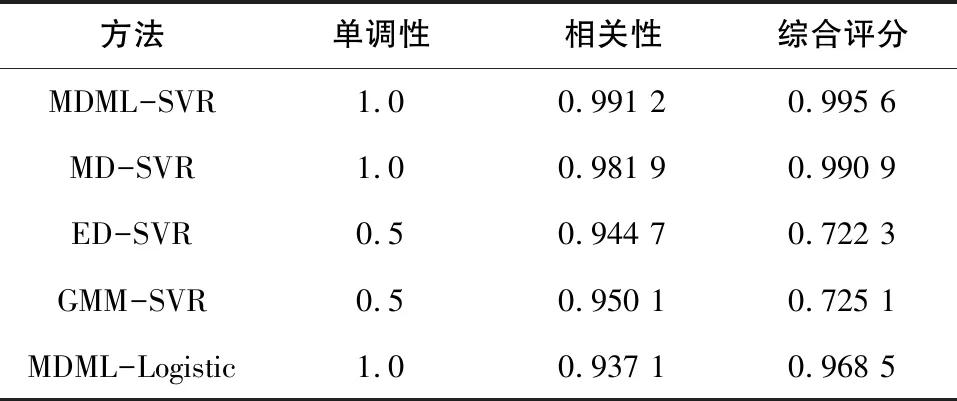
表3 健康指标评分

采用方均根误差(RMSE)、平均绝对误差(MAE)、平均百分比误差(MAPE)对健康评估结果进行评价，结果见表4。MDML-SVR的RMSE、MAE、MAPE分别为0.047 3、0.027 8、0.036 4，均优于其他方法。综合以上分析，本文所提健康评估方法效果优异，可以有效提高行星齿轮箱健康评估准确率。

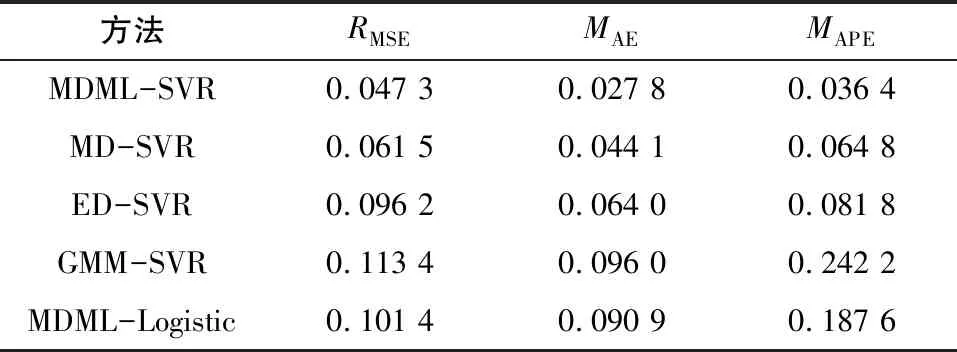
表4 健康评估误差比较

5 结语

提出一种基于图谱特征与度量学习的行星齿轮箱健康评估方法，通过实验结果分析，得出结论：

1) 图谱特征作为故障特征参数，在表征故障严重程度方面优于常用的时域、频域特征。

2) 将单调性与相关性作为度量学习准则，可以减小不同故障严重程度下马氏距离的波动，提高健康评估指标的单调性、准确性。

3) 基于MDML-SVR的行星齿轮箱健康评估方法评估结果更准确。