基于HHT和GA-BP的电压暂降源定位方法

杨桢，马钰超，李丽，李鑫，马子莹

(1. 辽宁工程技术大学 电气与控制工程学院，辽宁 兴城 125105；2. 国网辽宁省电力有限公司阜新供电公司，辽宁 阜新 123000；3. 国网冀北电力有限公司唐山市丰南区供电分公司，河北 唐山 063000)

0 引言

根据电力部门的相关统计，在电能质量问题中，80%以上都是由电压暂降引起的[1]，这造成了巨大的经济损失[2]。其中，大部分电压暂降事件是由短路造成的，因此，电压暂降源的精确定位具有重要意义。

对于电压暂降源的定位，国内外学者进行了大量的研究，主要根据故障时监测装置上下游电气量变化的不同提取特征值，常用方法有短时傅立叶变换法（STFT）[3-5]、小波变换[6-9]和S变换[10-13]，但是这些方法都受Heisenberg测不准原理的制约。在此基础上，用神经网络对特征值进行分类从而判断出电压暂降源相对于监测装置的上下游关系，学者们主要采用了反向传播（backpropagation，BP）神经网络[14-15]、RBF（径向基函数）神经网络[16]、概率神经网络（PNN）[17]和支持向量机（SVM）[18]。然而这些方法容易陷入局部收敛甚至不收敛的情况，定位的准确率比较低，有的学者采用了最小二乘法[19]，但是随着网络结构的复杂化，这种方法定位误差也会随之增大。

针对传统提取特征值受限于Heisenberg测不准原理的缺点，本文用基于集合经验模态分解（EEMD）的希尔伯特-黄变换（HHT）来提取有效特征值。并用遗传算法（GA）对BP神经网络进行优化，以避免BP神经网络陷入性能洼地。把有效特征值作为GA-BP神经网络的输入，针对不同的短路故障分别进行定位。得到初步故障源后，以故障位置、过渡电阻为优化变量，采用飞蛾扑火优化（MFO）智能算法进行求解从而得到精确定位。同时，根据三相电压幅值之间的关系判断出故障类型。最后以双电源系统为例，进行建模仿真，验证该定位方法的可行性。

1 电压暂降源上下游的判定

在图1所示的双电源系统中发生电压暂降时，故障点位置不同，监测装置处的电压和功率电流的变化也会有所不同[20]。监测装置M的上下游设有故障f1和f2，当f1发生故障时，监测装置M测得的电压和功率电流都会变小。当f2发生故障时，M测得的电压值会变小，但是功率电流会变大。

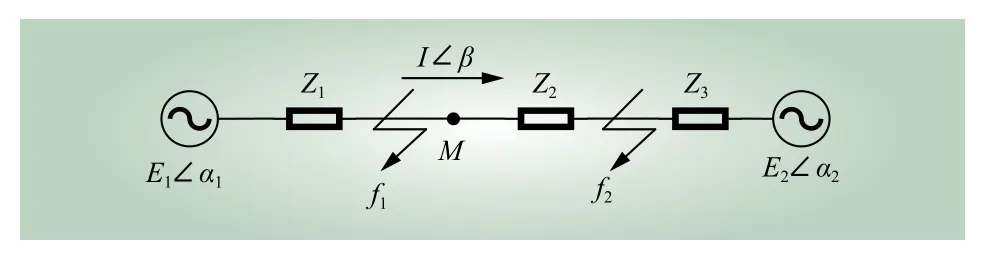
图1 暂降定位分析Fig. 1 Voltage sag location analysis

故障发生前，M处的电压为

等式两边乘以电流的共轭复数I*，提取实部后可简化为

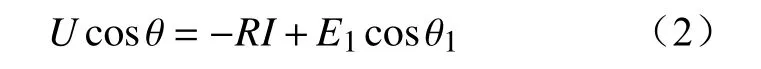
式中：θ为M点处的功率因数角；θ1为电源E1与电流I的相位差。

当f2发生故障，电流由E1流向短路故障点，则 cosθ＞0，|Ucosθ|=Ucosθ，采样点（I,|Ucosθ|）就在斜率为-R的曲线上；若f1发生故障，电流由E2流向短路故障点，则 cosθ＜0，|Ucosθ|=（-Ucosθ），采样点（I，|Ucosθ|）就在斜率为+R的曲线上。同时，功率电流I和|cosθ|都降低的情况下，扰动源位于监测点的上方；功率电流I增大而|cosθ|减小的情况时，扰动源位于监测点的下方，这样系统斜率仍符合。对于不同的故障点，取监测装置暂降前后测得的电压实部与功率电流值进行线性拟合可得图2曲线，从而可以得到系统轨迹斜率k。

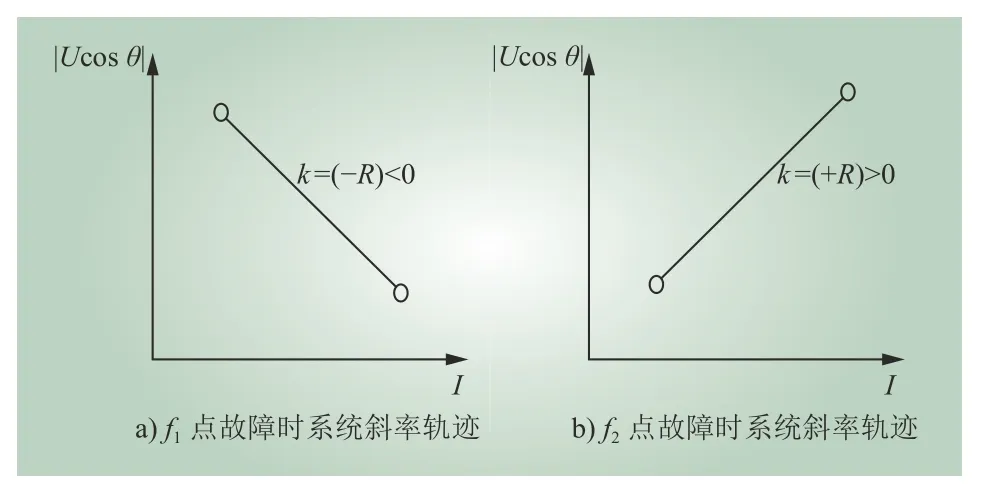
图2 |Ucosθ|- I拟合曲线Fig. 2 |Ucosθ|- Ifitting curve

在图3所示的双电源系统故障电路中，若故障X发在监测点M1的前方，电流由E1流向X，电流实部Icosθ＞0，故障位于监测点下游；若故障X发在监测点M2的后方，电流由E2流向X，Icosθ＜0，故障位于监测点上游。所以同时可以根据电流实部Icosθ来判断电压暂降源的位置。

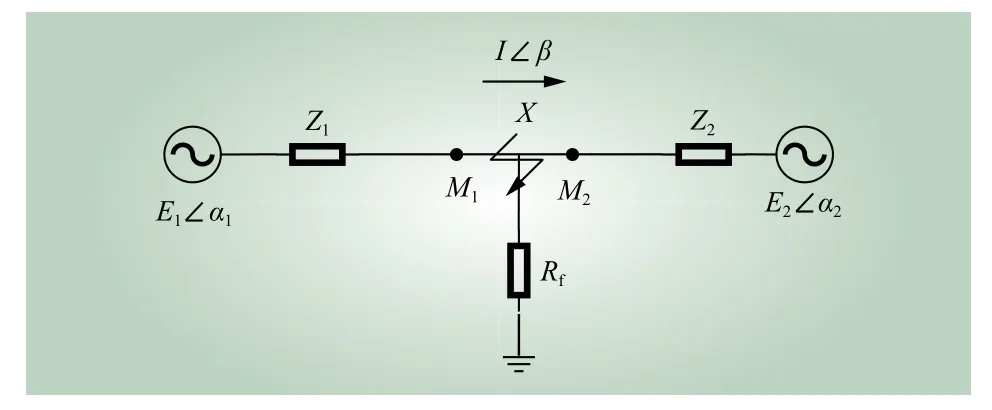
图3 双电源系统电路Fig. 3 Dual power supply system circuit

2 电压暂降源的精确定位及故障源的分类

对故障源进行定位时，主要包括有效特征值的提取、神经网络初步定位、优化算法精确定位。定位流程如图4所示。

图4 电压暂降源定位流程Fig. 4 Voltage sag source location flow chart

2.1 有效特征值的选取

使用基于EEMD的HHT对Matlab仿真所获得的故障信号进行处理，经过计算后获取有效特征值电流实部Icosθ和系统轨迹斜率k。

2.1.1 集合经验模态分解（EEMD）

EEMD是在EMD的基础上添加高斯白噪声的自适应分解方法，从而可以避免经验模态分解（EMD）中的模态混叠现象[21]。

EEMD对故障信号进行多次分解，可以将其分解为一组固有模态函数（intrinsic mode functions，IMFs）。经EEMD分解后的故障信号为

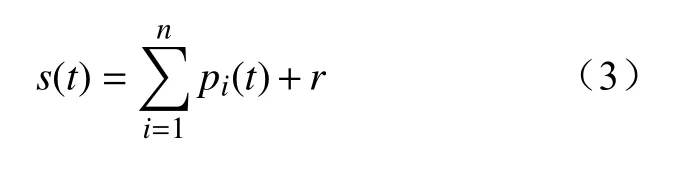
式中：n为IMF的总数；pi（t）为第i个IMF的分量；r为附加白噪声的余项。

2.1.2 有效IMF分量的选取

2.1.3 希尔伯特变换（HT）

2.2 BP神经网络的优化和故障定位

用GA对BP神经网络进行优化，增加其分类性能的优越型，然后将有效特征值作为神经网络的输入得到故障源的初始位置。

2.2.1 GA优化BP神经网络

在BP神经网络中，初始状态值一般，由系统随机产生，容易造成BP神经网络振荡或者局部收敛，甚至出现不收敛的情况。本文用到的BP网络如图5所示。用遗传算法选出最优的染色体个体，即最优的初始权值和阈值，从而避免BP神经网络陷入性能洼地。

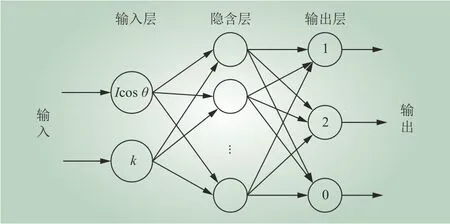
图5 BP神经网络Fig. 5 BP neural network

在用遗传算法优化BP神经网络时，先确定BP神经网络拓扑结构，根据BP神经网络的权值阈值长度设定GA中每个个体的染色体数目。将BP神经网络训练误差设为适应度值，选取各代种群中适应度值最小的染色体作为最优染色体，即BP神经网络的初始权值和阈值，图6为GA-BP算法分类的流程。

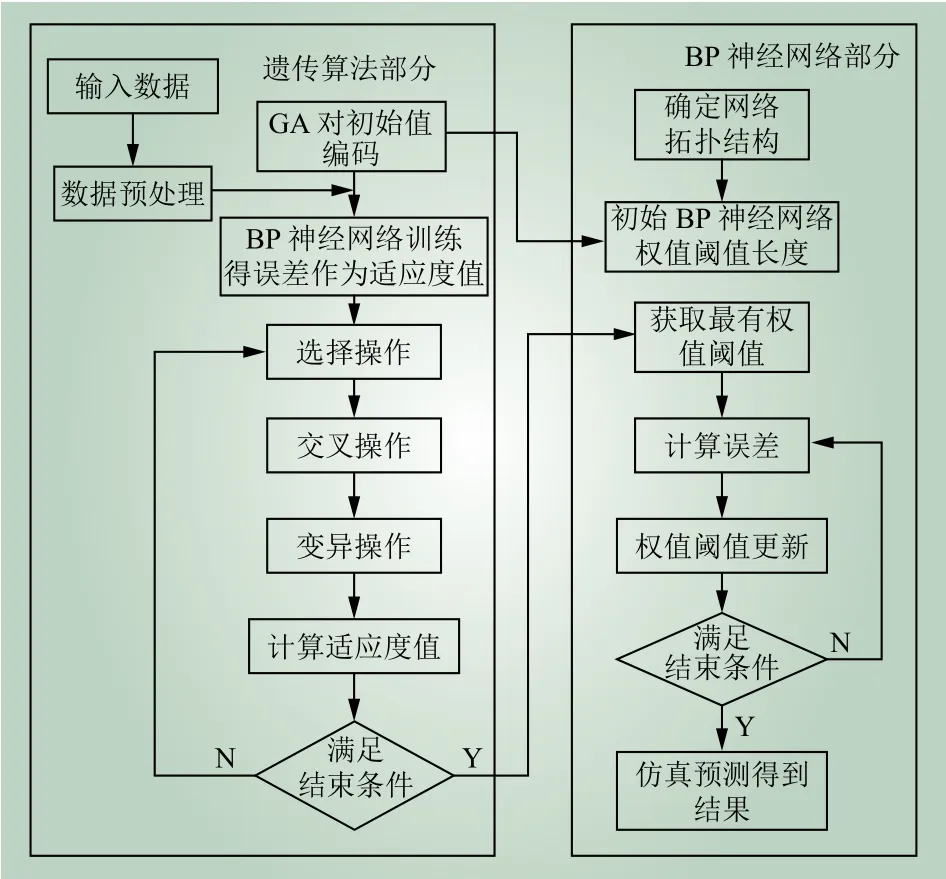
图6 GA-BP算法流程Fig. 6 GA-BP algorithm flow chart

2.2.2 故障线路及上下游的定位

在2.1节获取的有效特征值中，随机选取总样本的2/3设为训练集样本，剩下的设为测试集数据。

分别对每个监测装置处的数据进行分类，在获取各监测装置上下游定位结果后求取电压暂降源的交集，从而实现电压暂降源的初步定位。

2.2.3 对故障源进行精确定位

在得到故障源的初步位置后，以电压电流的实际值与观测值的误差为目标函数进一步来获取故障源的精确定位[22]。

（1）优化变量。本步优化以故障发生支路l（离散型）、故障点距故障支路首段相对距离 γ （连续型）和过渡电阻Rf（连续型）为优化变量。

（2）目标函数。本步优化亦以观测点处的故障后电压、电流的理论计算值与实际观测值的误差值的总和最小为目标，具体为

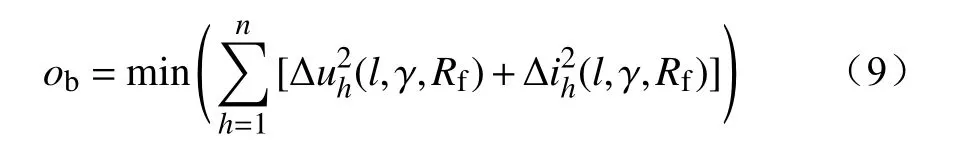
式中： Δuh(l,γ,Rf)、 Δih(l,γ,Rf)为故障支路l上、距离支路首端的相对距离为 γ 且过渡电阻为Rf时，第h个监测装置处的电压、电流误差值。

（3）约束条件为

式中：Rlim为过渡电阻上限，本文中设置为40 Ω。

对于上述的混合优化问题，采用文献[23]提出的飞蛾扑火优化（MFO）算法进行求解，解得γ的值即可知道故障源的具体位置。

2.3 故障类型的分类

假设故障前电压标幺值为1，故障期间电压为U，若未故障相电压也发生变化，则规定其为U，故障相电压可以根据U求得。不同电压暂降类型的各相电压幅值计算方法如表1所示。

表1 不同类型故障时各相电压幅值Table 1 Voltage amplitude of each phase under different faults

通过式（5）～（7）对仿真得到的故障数据进行计算求取不同故障时各相电压的幅值。根据表1中三相电压的关系，从而判断出故障类型。

3 仿真验证

在Matlab/Simulink中根据文献[24]搭建图7所示的双电源系统，E1=110 kV、E2=10.5 kV，系统频率为50 Hz，变压器及其他负载情况、接线方式见图7。针对对称故障和非对称故障三相电气量变化不同的情况，本文在仿真模型中分别设置F1（在N1-N2线路上离N1节点30%处发生A相接地故障，过渡电阻为20 Ω），F2（在N2-N4线路上离N2节点50%处发生A、B两相相间短路故障，过渡电阻为10 Ω），F3（在N3-线路上离N4节点70%处发生A、B两相接地短路，过渡电阻为10 Ω）和F4（在N4-线路上离N5节点80%处发生A、B、C三相短路，过渡电阻为5 Ω）4种不同的故障，仿真时间为1 s，故障时间设置为0.4～0.6 s。根据文献[25]的监测装置布点方法，在电路系统设有m1、m2、m3、m44个监测装置，监测装置的监测电压阈值设为电压有效值的90%。对于不同的故障，图8列出了电压暂降时部分监测装置监测的电压有效值。

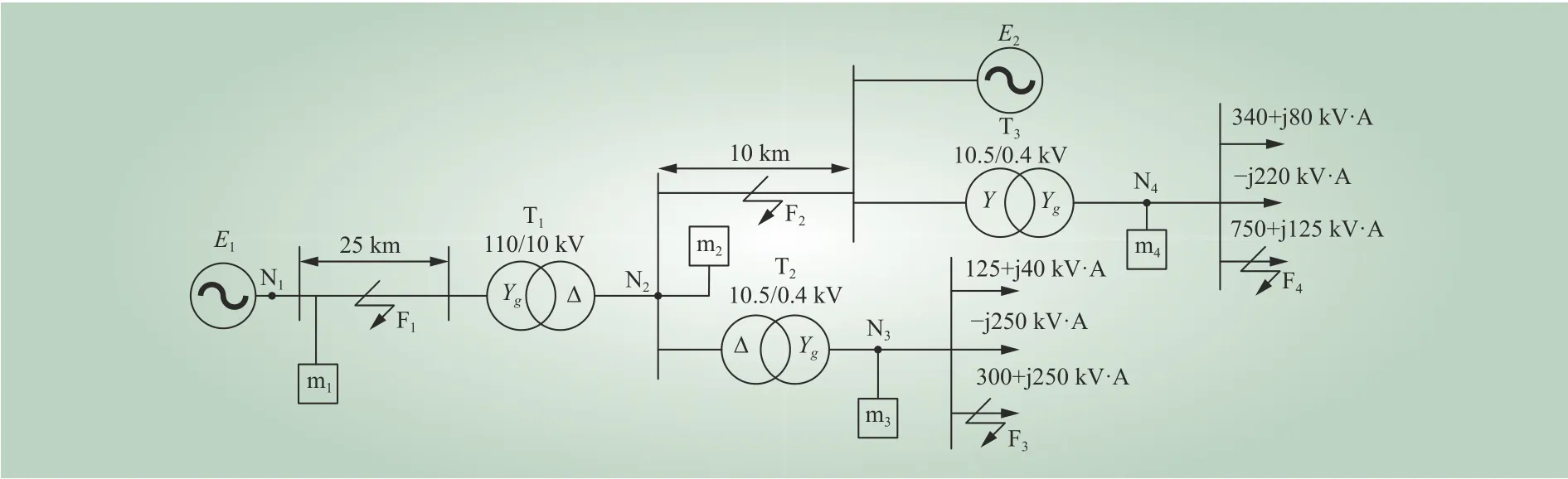
图7 双电源供电系统Fig. 7 Dual power supply system

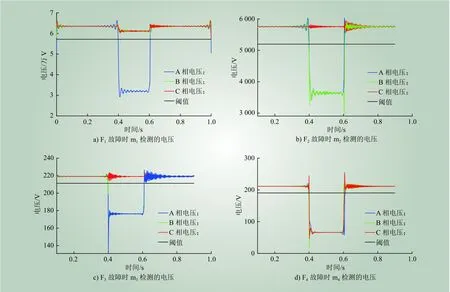
图8 不同故障的仿真结果Fig. 8 Simulation results of different faults

3.1 仿真结果分析

3.1.1 神经网络上下游的定位

在图8所示的故障中，对于不同的故障，先用训练数据对神经网络模型进行训练，然后分别用GA-BP和传统的上下游定位方法BP、RBF、PNN、SVM对测试集进行验证，结果如表1所示，各神经网络定位方法准确率可表示为

式中：n为样本集总数量；m为准确分类数量。

从表2的结果可以求出，在传统定位方法中，定位效果最好的BP神经网络平均准确率为86.67%，而本文提出的GA-BP定位方法的平均准确率达到了99.4%，明显优于其他定位方法，能够准确地定位出故障源相对于上下游的位置。

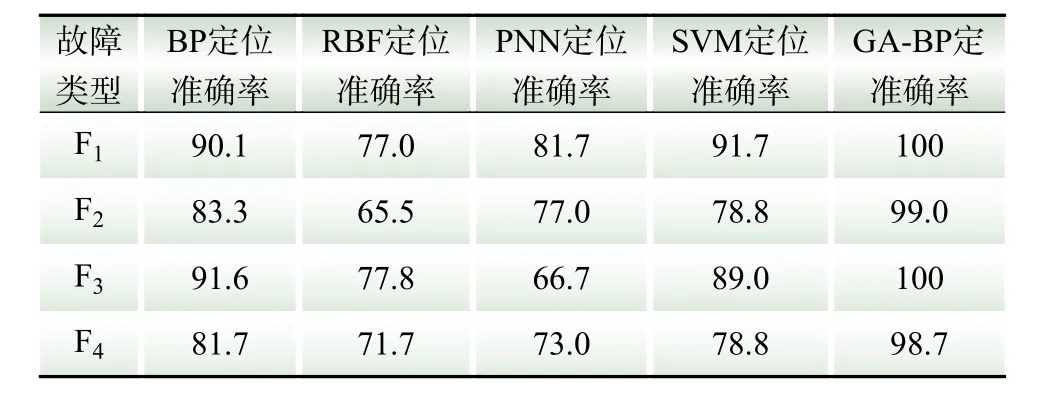
表2 定位准确率的对比Table 2 Comparison of positioning accuracy%

在用GA-BP对有效特征值进行分类时，对于不同故障神经网络对各监测装置的分类结果如表3所示。

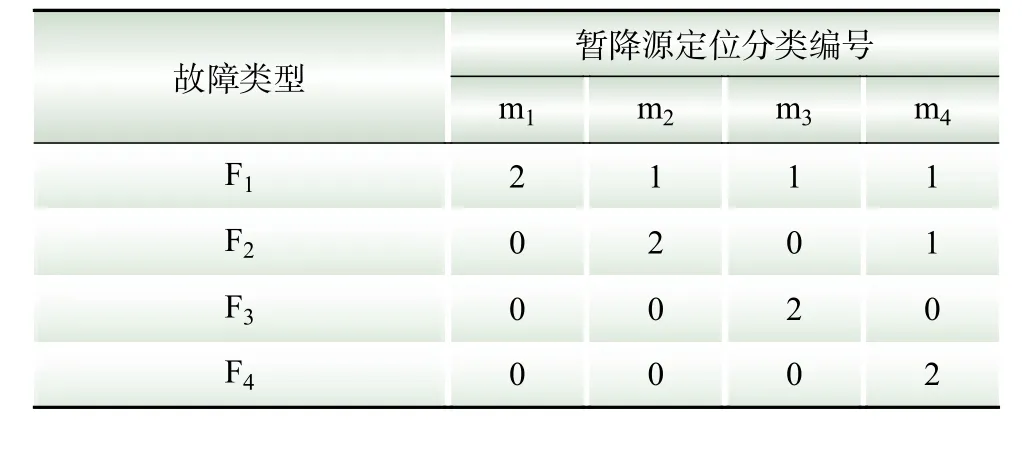
表3 GA-BP神经网络定位结果Table 3 GA-BP neural network location results

表3中：1代表电压暂降源位于监测装置的上游；2代表电压暂降源位于监测装置的下游0代表监测装置未检测出电压暂降；mi（i∈1～4）为不同位置的监测装置。

根据表3可知，对于F1故障，电压暂降源在监测装置m1的下游，在其他3个监测装置的上游，从而可以推断出，电压暂降源位于N1-N2线路上。类似的，可以推断出F2、F3、F4分别位于N3-N5、N4-、N5-线路上。

3.1.2 精确定位

在得到初步故障源位置后，根据2.2.3节的精确定位模型求取 γ 值，从而得到精确故障源，所得结果见表4。

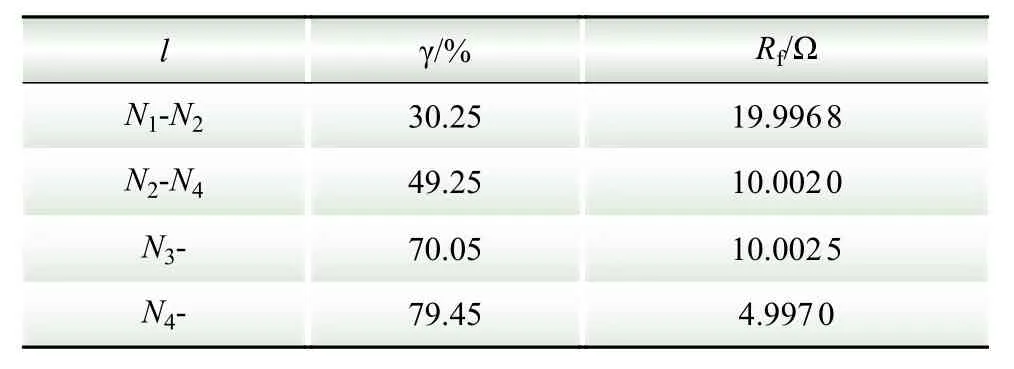
表4 精确定位结果Table 4 Precise positioning result

从表4可知，对于4种故障类型，故障源定位结果准确；定位模型求得的 γ 值与仿真模型中设定的 γ 误差分别为0.25%、0.75%、0.05%、0.55%，最大误差仅为0.75%，定位精度较高。

3.1.3 故障类型的分类

从图8a）可以看出，A相电压在0.4～0.6 s处发生暂降，而B、C两相电压基本保持不变，根据表1中三相电压的关系可以推断出图8a）中所示故障为A相短路。同理可以推断出图8b）为A、B两相相间短路，图8c）为A、B两相接地短路，图8d）为三相短路故障。推断结果与Matlab仿真设置相同。

4 结论

针对传统提取特征值的方法受Heisenberg测不准原理制约的现象，本文采用基于EEMD的HHT对Matlab中的仿真数据进行处理得到有效特征值，同时用遗传算法对BP神经网络进行优化来避免性能上的洼地。将提取的特征值作为神经网络的输入来对故障源进行初步定位。然后用MFO算法对故障线路的电压电流构建的数学模型求解，获取距故障线路首端的相对距离 γ 值从而实现精确定位。同时，根据三相电压幅值之间的关系判断出故障类型。在双电源系统的仿真模型中分别对不同类型的短路故障进行仿真验证，从仿真结果可以看出，本文所提出的方法初步分类的平均准确率为99.4%，相对于传统方法能够大幅提高定位的精确度，在进行精确定位时最大误差也仅为0.75%，定位精度较高，根据三相电压之间的关系也能正确地推断出故障类型，在实际应用中具有很好的前景。