基于能量函数法的光伏和火电联合外送多机系统暂态稳定性分析

亢朋朋，毕立松，孙谊媊，郭小龙，杨桂兴

（1.国网新疆电力有限公司，新疆 乌鲁木齐 830002；2.北京科东电力控制系统有限责任公司，北京 100085；3.新疆大学，新疆 乌鲁木齐 830046）

0 引言

在第75届联合国大会上，我国提出了要采取更加有力的措施以应对日益严重的环境问题，即要在2030年前实现碳达峰，在2060年前实现碳中和的目标。含大规模光伏、风电等并网新能源电力系统的的高效利用已成为未来我国能源体系发展的趋势[1]，[2]。然而，光伏和风电具有波动性、随机性，大规模光伏、风电等新能源电力的接入，会影响传统电力系统结构及其暂态运行稳定性。光伏、风电等新能源渗透率高、出力的随机波动性强、故障干扰随机性较大，这些特性均会对含光伏和风电机组电力系统的暂态运行稳定性造成影响，甚至会引发大规模光伏机组并网解列，威胁整个电力系统的安全稳定运行[3]～[5]。为了满足新型电力系统稳定运行的要求，须对光伏和火电联合外送系统运行暂态稳定性进行研究。

一些学者研究了光伏、火电打捆联合外送对电力系统运行稳定性的影响。文献[6]通过对不同并网控制方式下光伏与火电打捆联合外送系统运行振荡的研究，分析了大型光伏电站并网后发生振荡的方式及其影响机理，提出了基于自抗扰控制技术的光伏、火电联合系统运行振荡抑制方法。文献[7]通过对“双高”电力系统运行特性的分析，提出了一种新的“双高”电力系统稳定性分类讨论方法及分析控制框架。文献[8]针对大规模光伏发电集中并网与火电打捆外送时的电网运行稳定性问题，研究了光伏大量接入安徽六安电网后的稳定运行控制方法，并根据实际运行情况分析该方法的应用效果。文献[9]，[10]研究了大规模光伏接入系统后，不同接入位置及不同渗透率造成系统潮流的改变，从而带来对系统阻尼特性、振荡模态的影响，随着渗透率的升高，会恶化区域振荡模态的特征根。文献[11]通过建立单级、双极型光伏电站并网发电模型，仿真研究了光照强度改变下光伏电站并网对电力系统电压、功率波动的动态影响。文献[12]，[13]研究了当光伏渗透率达到一定比例时，对并网联络馈线电压稳定性和互联输电网络电压稳定性、静态稳定性和暂态稳定性的影响。文献[14]通过建立含光伏机组的电力系统四阶模型，深入研究分析了受光伏出力波动影响而引起系统扰动的电力系统运行稳定性。上述文献虽然研究了不同规模下的光伏机组出力对电力系统运行稳定性的影响，但是对于含大规模光伏机组并网的“光火打捆”联合外送系统来说，其系统运行稳定的关键还是在于不同动态运行状态下，因光伏机组出力波动导致系统输送功率发生突变或引发短时运行故障时系统能否实现暂态稳定运行。

本文采用能量函数法推导出含光伏机组的电力系统不平衡运行状态下系统暂态势能，建立了含光伏机组的电力系统能量函数模型；分析了光伏机组输出功率对系统暂态稳定性影响和系统暂态能量变化特性；利用电力系统节点导纳方程，推导出大规模光伏机组接入后，光伏火电联合外送多机系统节点导纳变化规律；建立了光伏和火电联合外送的多机系统暂态能量函数模型，分析光伏机组出力变化下多机系统暂态功角变化规律。通过搭建的仿真模型，仿真分析了光伏和火电联合外送系统的暂态稳定性变化，确定系统的暂态稳定性。

1 含光伏机组的电力系统能量函数模型

大规模光伏机组发电并网相当于改变了传统电力系统的网架结构。系统网架结构的变化及光伏机组出力波动性的变化会引起电力系统暂态能量聚集的改变，影响原有电力系统运行的暂态稳定性。本文采用能量函数法，通过分析大规模光伏机组接入后光伏和火电联合外送多机系统运行暂态能量变化过程，对多机系统暂态稳定性进行分析、判定，研究含光伏机组的无阻尼单机无穷大电力系统的运行过程暂态稳定性，建立含光伏机组的电力系统能量函数模型。

如图1所示，在双回线一侧的母线处接入一光伏机组，搭建含光伏机组的单机无穷大电力系统模型。其中，SG为火电厂同步发电机组，PV为光伏机组。

图1 含光伏机组的单机无穷大电力系统示意图Fig.1 Single-machine infinity system with photovoltaic unit

假设光伏机组由n串m列的光伏板组成，经逆变器、变压器后接入系统，则其模型为

式中：VPV为光伏机组交流侧输出电压；PPV，QPV分别为光伏机组交流侧输出的有功功率和无功功率；V′PV为光伏机组逆变器直流侧电压；xT2为变压器等效电抗；δPV为光伏机组逆变器的移相角。

如图1所示的系统运行至t时刻，在外送双回线中的某一回线路发生三相短路故障，系统在t=tc时保护装置切除线路故障。若在该过程中，不考虑线路保护装置重合闸的影响，且不计入阻尼，含光伏机组的单机无穷大电力系统在故障前、故障过程中和故障切除后火电厂同步发电机组输出功率分别为PSG1，PSG2，PSG3，则火电厂同步发电机组功角特性可以表示为

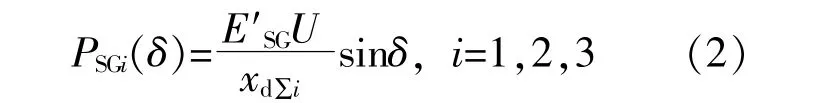
式中：U为单机无穷大系统的母线电压；E′SG为火电厂同步发电机组的暂态电势；xdΣi为整个系统的总电抗值；δ为火电厂同步发电机组的暂态电势E′SG与单机无穷大系统的母线电压向量之间的夹角。

在上述短路故障切除过程中，光伏机组并网发电功率发生变化会造成整个单机无穷大电力系统功率、潮流的波动。基于光伏机组模型，将光伏机组输出功率等效为接地的电导和电纳，分析短路故障切除过程中及故障后光伏机组出力波动对系统暂态稳定性和系统暂态能量变化特性的影响。故障后含光伏机组的单机无穷大电力系统可等效如图2所示。式中：yPV为光伏机组的等效接地导纳；xd为火电厂同步发电机组的暂态电抗；xT为系统中变压器的等效电抗；xL为故障后双回线中另一回线路电抗。

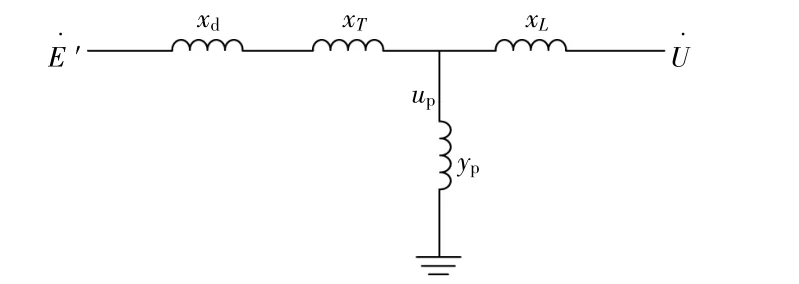
图2 故障后系统的等效电路图Fig.2 Equivalent circuit diagram of the system after failure

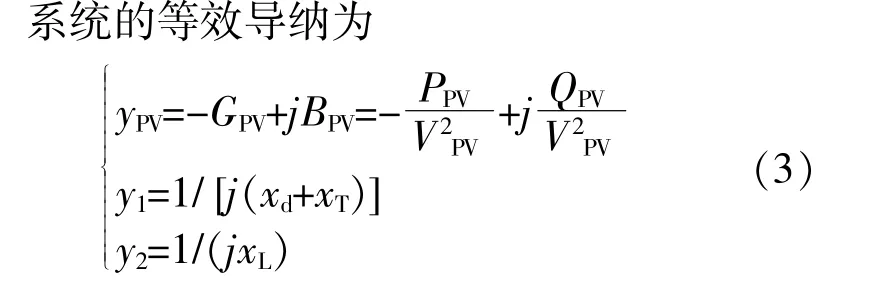
式中：PSGe为火电厂同步发电机组故障后的电磁功率；Y11，Y12分别为火电厂同步发电机组节点的自导纳和导纳；φ11，φ12为其导纳与电导之间的夹角；rPV为故障处接地电阻。

根据含光伏机组的单机无穷大电力系统的转子运行方程，在故障后系统趋于稳定时，PSGM-PSGe=0，可分别计算出系统在故障后处于暂态稳定时的功角δ1和处于暂态不稳定时的功角δ2。

式中：Vs（δ，ω）为单机无穷大电力系统以状态变量（δ，ω）的系统暂态能量函数；ω1为单机无穷大电力系统处于暂态稳定时的角速度；J为火电厂同步发电机组转子惯性时间常数。

当火电厂同步发电机组的转子运动至系统暂态不稳定平衡点δ2时，系统暂态运行至所能承受的最大暂态总势能。若系统在此时仍存以部分暂态动能，单机无穷大电力系统失步，系统处于暂态不稳定平衡点，即临界不稳定状态点δ2下的系统暂态总势能为

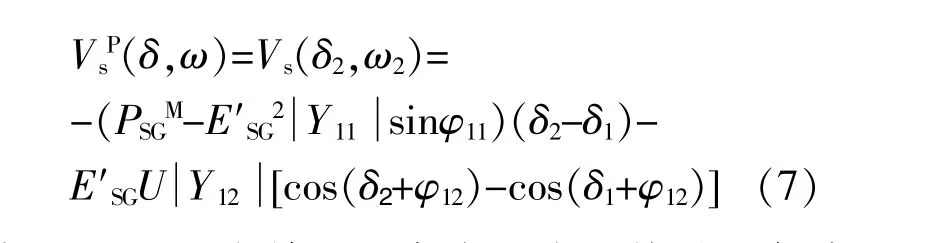
式中：VsP（δ，ω）为单机无穷大电力系统处于暂态不稳定状态下的系统总暂态势能；ω2为单机无穷大电力系统处于暂态不稳定时的角速度。

从式（4）～（7）可以看出，系统中光伏机组出力波动时，其输出有功功率增大会使Y11，Y12数值、火电厂同步发电机组故障后的电磁功率增大；输出无功功率增大会使得Y11，Y12数值、火电厂同步发电机组故障后的电磁功率减小，对火电厂同步发电机组输出的电磁功率造成波动，进而改变单机无穷大电力系统的暂态能量及状态量，影响系统的暂态稳定性。

对单机无穷大电力系统转子运行方程两侧积分，并代入式（7），可计算得出t时刻单机无穷大电力系统暂态能量函数：

式中：ω0，δ0分别为单机无穷大电力系统基准角速度和功角。

在Vs（t）达到VsP（δ，ω），火电厂同步发电机组输出电磁功率增加时，故障过程中单机无穷大电力系统暂态能量达到暂态不稳定平衡点δ2的系统总暂态势能的时间也越长。这就使得单机无穷大电力系统在故障过程中各个时刻的系统暂态能量均会减小，单机无穷大电力系统也会更趋于稳定状态。

2 光伏和火电联合外送多机系统暂态稳定性分析

假定光伏和火电联合外送多机系统网架结构在含光伏机组的单机无穷大电力系统中扩展为含有N个节点、M个火电厂同步发电机组、K个光伏机组、l条系统支路和M0个负荷点的多机系统，其中，M+1节点至M+K节点处接入光伏机组。多机系统部分模型可表示为

将上述搭建的光伏和火电联合外送多机系统中的多个火电厂发电机组与负荷点映射、等值为如图1所示的单机无穷大电力系统。考虑在M+1节点至M+K节点处接入光伏机组，整体分析光伏机组接入后对原有电力系统运行暂态稳定性的影响。

将火电厂同步发电机组和光伏机组映射为送端系统机群Se，负荷点映射为受端系统机群Re，则送端系统机群Se和受端系统机群Re的系统功角、系统惯性时间常数、系统输出机械功率和系统输出电磁功率可以等值为

将式（15）代入式（11）可见，光伏机组出力波动在引起送端系统机群Se内节点自导纳矩阵发生改变后，造成等值系统输出电磁功率恒定量PSe/Ree0发生变化，等值系统输出的机械功率也因此发生改变，进而影响光伏和火电联合外送多机系统运行暂态稳定性。

式中：VMulti（δSe，δRe，ωSe，ωRe）为光伏和火电联合外送多机系统以状态变量（δSe，δRe，ωSe，ωRe）的系统暂态能量函数，前两项为光伏和火电联合外送多机系统的暂态总动能，中间两项为光伏和火电联合外送多机系统的暂态总势能，最后一项为光伏和火电联合外送多机系统网络结构中存储的能量，反映了不同发电机组间功率波动引起的暂态势能变化；δSes，δRes和ωSes，ωRes分别为故障后光伏和火电联合外送多机系统达到稳定平衡点时，送端系统机群Se和受端系统机群Re功角差和转子角速度。PSe，PRe分别表示为

同式（7），代入光伏和火电联合外送多机系统暂态不稳定平衡点状态变量，即可计算出光伏和火电联合外送多机系统处于暂态不稳定状态下的系统总暂态势能。

3 算例分析

根据以上模型分析，选取相应的光伏机组并网运行数据，利用PSD-BPA机电暂态仿真软件,搭建光伏和火电联合外送多机系统仿真模型，并按照文中的方法将系统中的多个火电厂发电机组与负荷点进行映射和等值为如图1所示的单机无穷大电力系统模型。其中，系统中火电厂同步发电机组容量为150 MW，接入的光伏机组容量为75 MW，经并网双回线外送电力。设定外送双回线中某一回线路的某处位置发生三相短路接地故障，且故障位置接地电阻rPV=5Ω，并设定故障开始的时刻t=0 s。另外，系统基准电压设为线路额定电压等级，火电厂同步发电机组xd=0.1，变压器xT1=0.232，xT2=0.232，线路xL=0.646。仿真计算中光伏机组采用MPPT控制方法，分析光伏机组出力波动对含光伏机组的联合外送多机系统运行暂态稳定性的影响。

通过仿真分析和计算，得出原有电力系统运行过程中处于暂态不稳定平衡点下的系统暂态总势能VsP=1.378 9，系统暂态稳定时的功角δ1=0.529 6和系统临界故障切除时间为0.11 s。不同故障切除时间下，原有电力系统中火电厂同步发电机组功角仿真结果示于图3，其结果与计算结果一致。

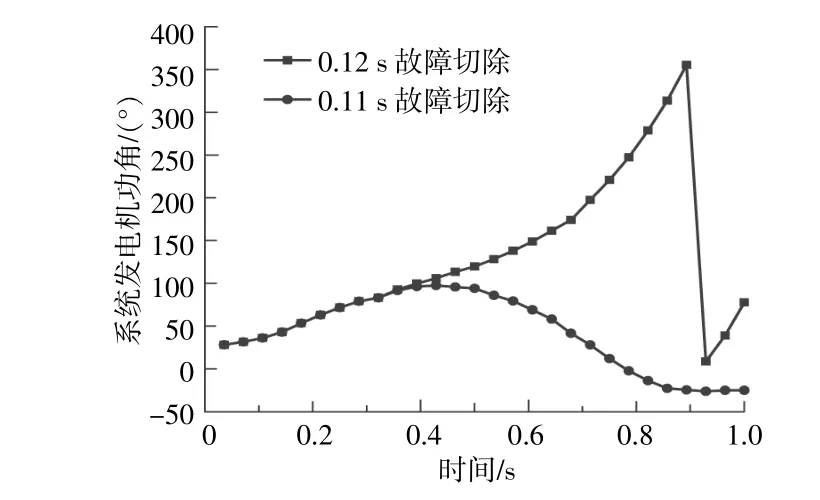
图3 不同故障切除时间火电功角仿真曲线Fig.3 Simulation curves of thermal power angle at different fault removal times

考虑光伏机组接入联合外送多机系统发生三相短路接地故障，根据建立的多机系统暂态能量函数，可以得出联合外送多机系统处于暂态不稳定平衡点下的系统暂态总势能VsP=3.273 1。联合外送多机系统故障切除后，系统暂态总动能、暂态总势能以及系统暂态能量变化曲线如图4所示。

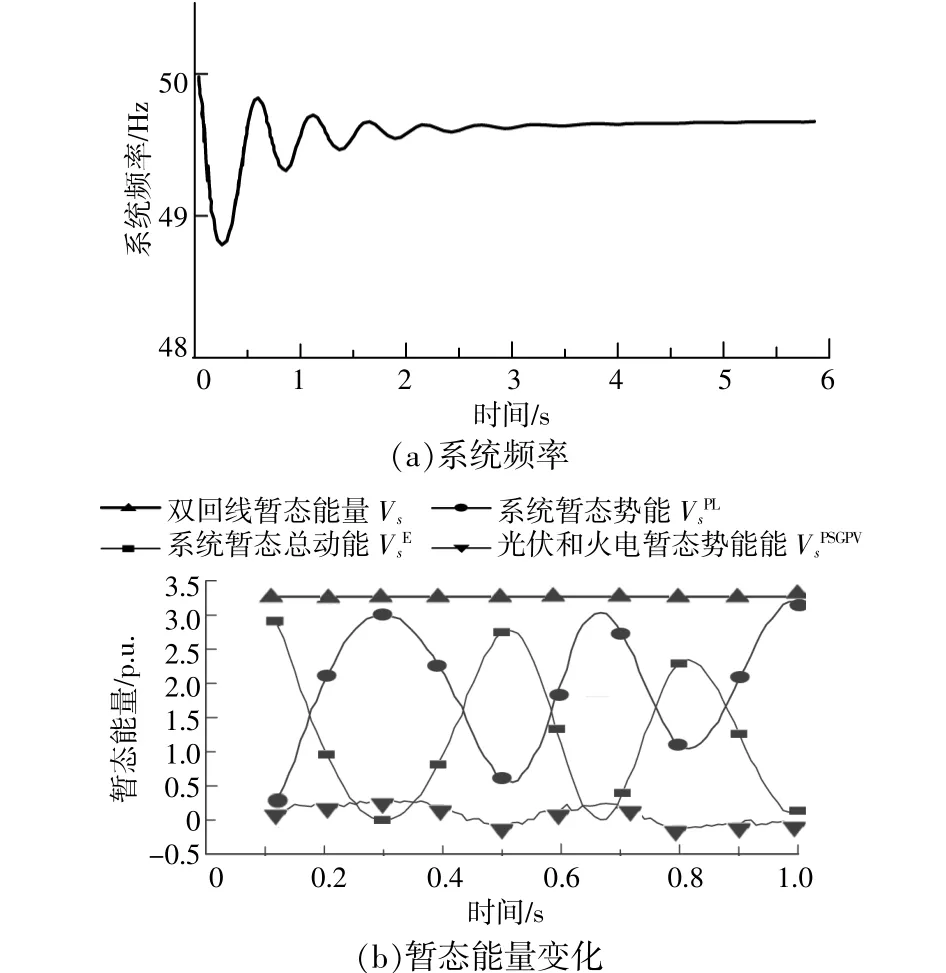
图4 联合外送多机系统仿真曲线Fig.4 Simulation curve of joint delivery multi-machine system

从仿真分析结果可以看出，在发生三相接地短路故障后，大规模光伏机组的接入使原有电力系统处于暂态不稳定平衡点下的系统暂态总势能有所增加，增强了原有电力系统能够遭受的最大系统暂态能量极限。从图4中可以看出，在将光伏和火电联合外送多机系统通过映射、等值为含光伏机组的单机无穷大系统后，其故障过程中系统暂态势能存在于整个系统网络支路当中，且各网络支路暂态势能变化和系统暂态总动能,均处于暂态不稳定平衡点下的系统暂态总势能以下，故障切除后系统处于暂态稳定状态。光伏机组的接入，虽然使得原有电力系统网架结构发生改变，增加了电力系统运行调度的困难，但在一定程度上提升了整个电力系统的稳定运行能力。

分析不同光伏机组运行控制方法对联合外送多机系统运行暂态稳定性的影响,设定两种控制方法：控制方法一为本文光伏机组控制方法，且发生故障后系统有无功输出；控制方法二为光伏机组发生故障后仅输出有功。不同光伏机组运行控制方法下单机无穷大电力系统运行暂态稳定性仿真结果如图5所示。

根据仿真软件的结果可以得出：故障期间采用控制方法一，光伏机组有功输出为0.087 5、无功输出为0.112 4；采用控制方法二，光伏机组有功输出为0.139 6。对比发现，由于采用控制方法一，在故障期光伏机组使火电厂同步发电机组输出的电磁功率增加，系统暂态能量达到暂态不稳定平衡时的系统总暂态势能的时间相对增加，含光伏和火电的联合外送多机系统运行暂态稳定性更好。

4 结束语

通过对光伏机组接入后光伏和火电联合外送多机系统在发生故障后系统运行暂态稳定性变化的规律研究，提出了一种基于能量函数法的光伏和火电联合外送多机系统暂态稳定性分析方法，建立了含光伏机组的单机无穷大电力系统能量函数模型。将光伏和火电联合外送多机系统映射、等值为单机无穷大电力系统，分析了多机系统在故障过程中系统运行暂态稳定性。

采用所搭建的仿真模型，仿真分析了光伏机组接入后系统暂态能量的变化，并参考光伏机组的不同控制方法，分析对比了光伏机组对系统运行暂态稳定性的影响。研究结果表明，本文所提出的暂态稳定性分析方法是可行的、有效的。