重型车辆自动驾驶气制动自适应控制研究

黄露　姚丽　杨易　黄赞铭　周怡安

摘 要：重型车辆气制动自适应控制是一项重要的自动驾驶纵向速度控制功能，在应用中至关重要，例如上下坡匀速行驶、精准停车、不同载重的车速控制等。由于典型气动制动系统是固有的非线性特性，存在很大的不确定性，且重型汽车的纵向刹车控制受负载、路况、车况的影响较大，传统的PID控制器无法满足不同工况下重型车辆自动驾驶车速稳定控制要求。本文描述了重型汽车在自动巡航控制下气制动系统因车况不确定因素导致的制动力不足问题，提出一种基于气制动系统的自适应刹车控制模型，详细说明气制动自适应控制模型的优势、推导过程，以及问题解决的具体应用案例，并给出了完整的数据分析和试验验证过程。

关键词：重型车辆 气制动 模型参考自适应控制 PID 自动驾驶

1 引言

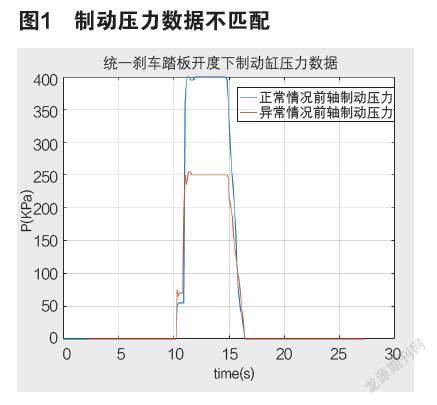
随着重型汽车（半挂卡车、货车、巴士等）的自动驾驶技术研究开始兴起、迭代和特定场景下的应用，汽车自动驾驶技术的研究近年来在国内外取得了巨大的进展。重型汽车的自适应巡航控制在应用中至关重要，不仅可以减轻驾驶员的负担，还可以使汽车的燃油供给和发动机功率间的配合处于最佳状态，有效地降低燃油的消耗和排气污染。因此，对汽车自适应巡航控制系统的研究具有重要意义。但是，重型汽车的纵向刹车控制受负载、路况、车况的影响较大。重型汽车的刹车系统一般采用气制动，存在典型气制动系统特有的非线性，且气制动系统在使用过程中，由于机件磨损或损坏，制动性能会下降，容易产生故障，危及行车安全。尤其对于重型车辆的自动驾驶系统，对车辆的刹车制动性能要求更加严格，一定程度的制动性能下降将导致自动驾驶系统无法良好实现车速平稳控制。因为重型汽车自动驾驶的制动减速控制采用电子制动踏板替代驾驶员的操作，通过电子制动踏板的开度控制制动阀打开输入足量的气压推动制动缸产生制动力，从而使车轮制动，车辆减速或停车。自动控制车辆完全停车或者以某一速度巡航是车辆纵向控制功能之一。特别是，重型汽车某些场景下必须能够施加非常精细的制动控制，以便准确地停在指定的地点。重型车辆气制动系统气压制动不良故障主要体现在重型汽车行驶过程中，实施制动时，车辆不能在短距离内减速停车，具体表现为制动失灵。通过对制动系统压力的分析发现，制动失灵的主要原因是输送到制动分泵的压缩空气压力不足，从而使得制动分泵产生的制动力不足。导致制动压力不足问题的主要原因有：制动踏板自由行程过大、制动阀的供气量不足、管路漏气堵塞等任一情况出现。相同的制动阀开度对应的制动缸压力数据如下图1所示，数据的结果显示同一制动压力目标（即相同制动阀开度）下，因管路堵塞导致制动缸压力不足。

目前国内外对重型车辆纵向控制的研究重点关注高速队列控制[1]和自适应巡航控制[2]。与车辆停车或精准制动控制相关的研究仅限于防抱死制动系统（ABS）[3]、车辆稳定性[4]或液压制动器[5]等。重型车辆基于气制动系统因自身原因导致制动力不足的控制器设计没有得到充分的研究。

本文对自动驾驶输出的制动力不足导致无法精准停车或精准速度控制问题进行详细的分析，建立基于制动压力的自适应控制模型，详细分析和推导了自适应模型的设计过程。采用模型参考自适应控制（MRAC）设计方法设计制动缸实际制动压力和目标制动压力的自适应律，通过调整控制模型的输出，尝试解决自动驾驶时气制动系统因制动阀问题导致制动力不足的问题。

本文介绍的应用实例是18米長的柳汽T7重卡带挂车辆在长沙智能网联测试区的实车测试验证。通过对算法模型进行推导和实车测试，对比自适应控制模型加入前后的制动缸压力实测数据，多方面的测试结果验证了制动系统的实际输出压力和目标制动压力基本匹配，带挂卡车满足控制目标减速停车要求。

2 重型汽车纵向动力学模型

沿车辆纵向的力平衡方程式如下[6]：

m x..=F x-F aero-R x-mg sin（θ） （1）

式中Fx为轮胎纵向力，Faero为纵向空气阻力，Rx为纵向滚动阻力，m为车辆质量，g为重力加速度，θ为车辆行驶的坡度。本文主要研究气制动的制动力控制，主要考虑的是Fx为制动时轮胎的纵向力，暂不考虑纵向空气阻力、纵向滚动阻力和重力的影响。车辆制动时产生制动力Fx作用于式（1），车辆产生加速度x..使车辆减速（x..<0）。气制动缸产生制动力公式：Fx=PS，S为制动缸活塞的有效面积，P为制动缸的压力，根据压力传感器测量获得。根据以上公式可得到车辆制动时加速度与制动缸压力的关系。重型汽车气制动的基本工作原理本文不再赘述，下面主要描述自动驾驶系统计算纵向加速度的过程。

目前车辆巡航控制系统典型算法是使用速度误差作为反馈的PID控制器[6]：

x..des（t）=-kp（vx-vref）—ki ∫t0（vx-vref）dt-kd[（ek-ek-1）] （2）

式中Vx为本车当前速度，Vref为期望的速度，ek为当前的速度误差，ek-1为上周期的速度误差。此算法只考虑期望的速度跟随，在重型汽车需要精准停车时不再合适，考虑加入位置误差的PID控制算法如下：

x.des（t）=-kp（sx-sref）-ki∫t0（sx-sref）dt-kd [（ek-ek-1）] （3）

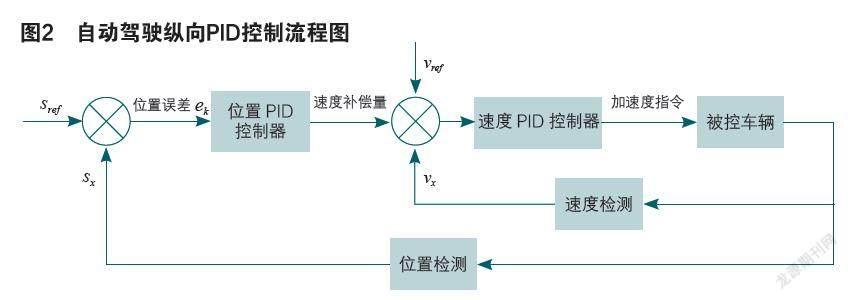
式中Sx为当前车辆所在位置，Sref为期望到达的位置，ek为当前的位置误差，ek-1为上周期的位置误差。将式（3）计算的x.des（t）即速度补偿量加入到式（2）中，即Vref =V+x.des（t）以此实现对车辆位置的精确控制。x..des（t）为自动驾驶纵向控制系统的期望加速度。需要减速停车时，自动驾驶系统根据期望位置误差和期望速度误差计算出期望的车辆加速度值，用于控制电子刹车踏板打开一定开度，制动缸冲入气压推动活塞使刹车片抱紧轮胎产生纵向制动力。控制流程如上图2表示。理想的情况下，上述过程可实现车辆按照期望的位置和速度减速停车。但是刹车系统的磨损和气路堵塞，例如气路有水汽导致比例阀堵塞充压不足时，同样的期望加速度产生的制动压力不一致，使得系统带来不确定的因素，如上图1中所描述的现象（从我们在柳汽T7半挂卡车自动驾驶实车停车测试的结果来看，每50次的停车测试，会出现2次车辆无法在期望位置停车）。因此，仅使用PID控制器对自动驾驶车辆期望的速度和位置控制无法满足制动系统异常情况下的减速停车要求。咨询有多年驾驶经验的重卡司机，人工驾驶时同样会出现脚踩同样深度制动踏板出现刹车制动力不足情况，当然司机在这种情况下会自觉地的加大脚踩刹车的力度使得刹车制动满足停车要求。通过大量自动驾驶实验数据分析，当气制动产生的制动效果不足时，体现在气制动缸压力与实际期望产生的制动压力存在误差。因此，本文考虑在原有的PID控制器基础上，针对期望的制动力和实际产生的制动力引入一种自适应控制算法，补偿制动压力不足的问题，实现期望制动力与实际制动力匹配。

3 模型参考自适应控制器设计

本文引入一种模型参考自适应控制算法[7]，并通过理论推导和稳定性分析，验证了自适应控制律的可良好解决气制动刹车制动力不足的现象。

3.1 模型参考自适应控制基本理论

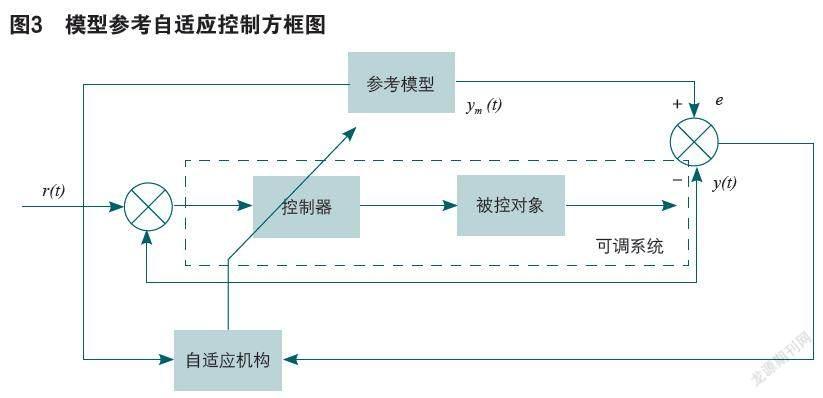
模型参考自适应控制的流程框图如下图3所示。

模型参考自适应控制流程图由两个环路组成，控制器和被控对象组成内环，描述为可调系统。由参考模型和自适应机构组成外环。对于重型车辆自动驾驶系统来看，该系统是在常规的纵向PID反馈控制回路上附加一个参考模型和自适应机构的自动调节回路组成。

对于重型车辆的纵向控制，当气制动刹车系统的制动力不足时，设计的自适应机构调整PID控制器的参数，增加控制器的输出加速度增大刹车力度（即模拟司机驾驶发现制动力不足时加大脚踩刹车踏板），以实现车辆按照期望的位置和速度自动驾驶跟停车。

3.1.1 基于lyapunov稳定性理论设计方法

模型参考自适应控制设计的方法有两种，一种为参数最优化方法，另一种为基于稳定性理论的方法。本文考虑基于lyapunov稳定性理论[7]方法设计重型车辆纵向控制的自适应控制律。

上文描述了重型车辆纵向控制器为PID控制器，其传递函数如下式（4）所示，为一阶系统。

（4）G（s）= kp + ki/s + kd s

本文定义一阶系统的状态方程如下：

（5）y. + ap y = bp u

设计参考模型如下：

（6）y. + am ym = bm r

r为参考模型输入，ym为参考模型输出， u为被控对象实际输入，y为被控对象实际输出。MRAC的目标：e=y-ym，当t→∞时， e→0，即参考模型接近于实际模型。

对式（5）两边加上amy：

（7）

式（7）减去式（6）：

（8）

（9）

令：，

则式（9）：

（10）

根据MRAC的目标 ：，当 t→∞时，，可知式（10）当t→∞时，满足条件

u-c0（t）y-d0（t）r=0

即：

u=c0（t）y-d0（t）r （11）

式（11）为设计的自适应控制律，使得当t→∞时，y渐近跟踪ym。

因y和r已知，所以需设计可调整的参数 c0（t）和d0（t）满足式（11）的要求。

利用lyapunov稳定性理论，决定c0（t）和d0（t）的自适应律参数，使得式（11）的输出满足当 t→∞ 时，的要求。对误差e 构建lyapunov的能量函数：

（12）

对式（12）两边求导：

（13）

需对式（10）进行简化，得到式（14）：

（14）

式（10）的簡化过程如下：

将式（11）代入式（5），

（15）

而，对两边求导

（16）

而  代入式（16），得：

令：

，

则推导出式（14）：

。

继续式（13）lyapunov能量函数的推导，代入式（14）得：

（17）

假定：

（18）

带入公式（17）得：

。

根据上式可知，对于任意e≠0，V是半负定的，即能量函数V是稳定的。根据lyapunov稳定性理论：若存在一个有连续一阶偏导数的正定函数V（x，t），V（x，t）满足下述条件：V·（x，t）为非正定（半负定）的，则该系统在原点处的平衡态是一致稳定的。因此，按式（18）c0（t）确定和d0（t），可保证式（14） 的稳定。

以上就是整个模型参考自适应控制基于lyapunov稳定性理论的推导过程，推导出的式（18）为自适应机构的自适应律。

4 实车测试数据分析

为验证模型参考自适应控制可以解决气制动刹车因自身问题导致制动力不足，本文作者在长沙智能网联汽车测试区使用柳汽T7带挂重卡空载工况下进行自动驾驶实车测试。为验证模型参考自适应控制算法的有效性，设计测试用例如下：

（1）选择测试路段为测试区的高速路段，路段长度1.5km。

（2）设计自动驾驶巡航速度为20km/h，固定每次测试自动驾驶终点及车辆停车点，以及自动驾驶起点。

（3）自动驾驶过程为加速、巡航、减速、停车。

通过调整气制动气压调节阀顶部的调整螺钉调小贮气缸气压，模拟刹车性能变差情况。

自动驾驶测试项分三项：第一项，正常贮气缸气压下采用PID控制算法，采集车辆停车时的速度和加速度变化情况;第二项，采用PID控制算法同时加入模型参考自适应控制算法，调小贮气缸气压下停车时的速度和加速度变化情况;第三项，未加入模型参考自适应控制算法仅采用PID控制算法，调小贮气缸气压下停车时的速度和加速度变化情况。对比三次试验的制动减速停车时速度变化曲线如上图4所示，加速度变化曲线如上图5所示，制动缸压力变化曲线如上图6所示。

从图4的速度数据曲线来分析，车辆速度从8.33m/s减速到0停车，第一项正常贮气缸气压下和第二项加入模型参考自适应控制算法但调小了贮气缸气压下的减速时间需要大约9s，第三项未加入模型参考自适应控制但调小了贮气缸气压下的减速时间需要大约12.5s。

从图5的加速度数据曲线来分析，车辆速度从8.33m/s减速到0停车，第一项正常贮气缸气压下和第二项加入模型参考自适应控制算法但调小了贮气缸气压下的加速度稳定在-0.85左右，第三项未加入模型参考自适应控制但调小了贮气缸气压下的加速度稳定在-0.6左右。

从图6的制动缸压力数据曲线来分析，车辆速度从8.33m/s减速到0停车，第一项正常贮气缸气压下和第二项加入模型参考自适应控制算法但调小了贮气缸气压下的制动缸压力稳定在350KPa左右，第三项未加入模型参考自适应控制但调小了贮气缸气压下的加速度稳定在255KPa左右。

从上述数据分析可以看出，加入模型参考自适应控制算法调整控制器输出，当制动缸的制动压力不足时，会自动增加控制器输出量，加大电子刹车踏板行程，提升刹车力度到控制系統的期望值。

5 结语

本文提出一种基于期望制动力和实际制动力的模型匹配自适应控制。设计过程包括问题提出、纵向动力学模型分析、模型参考自适应设计、稳定性推导、测试用例设计和实车测试验证。从这个设计过程和实车测试的数据分析来看，基于模型参考自适应控制理论推导的自适应机构可以通过调整控制器的输出良好实现期望值与实际输出值的匹配，良好模拟司机在制动减速时发现车辆制动力不足通过加大刹车踏板行程增大刹车力度的过程。上述控制算法可良好应用到重型车辆自动驾驶的纵向气制动控制模型中，测试用例的实验数据和后续的柳汽T7大量的自动驾驶实车测试也进一步说明控制器设计的有效性和鲁棒性。

参考文献：

[1]Rajesh Rajamani，Choi，S.B.，Law，B.K.，Hedrick，J.K.，Prohaska，R.，and Kretz，P.，2000.Design and experimental implementation of longitudinal control for a platoon of automated vehicles[J].Transactions of ASME，Journal of Dynamic Systems， Measurement，and Control，122（September），pp.470–476.

[2] Liang，C.，and Peng，H.，1999.Optimal adaptive cruise control with guaranteed string stability[J]. Vehicle System Dynamics，32（4），pp. 313–330.

[3]Hatipoglu，C.，Hai，Y.，and Ozguner，U.，2001.Self-optimizing brake control design for commercial vehicles[J].In SAE Technical Paper，no.2001-01-2731.

[4]Swaroop，D.，and Hedrick，J.K.，1996.“String stability of interconnected systems”.IEEE Transactions on Automatic Control，41（3），pp.349–357.

[5] Choi，S.B.，and Devlin，P.，1995. Throttle and brake combined control for intelligent vehicle highway systems[J]. In SAE Technical Paper，no.951897.

[6] Rajesh Rajamani主编，王国业，江发潮，张露译.车辆动力学及控制第2版[M].机械工业出版社，2018（4）：65-85.

[7]Nhan T. Nguyen，2018.Model-Reference Adaptive Control.Intelligent Systems NASA Ames Research Center Moffett Field，CA USA.pp.47-81，83-123.