比例时滞神经网络的时滞依赖全局多项式同步性

李 倩，周立群

（天津师范大学数学科学学院，天津 300387）

神经网络在过去几十年中发展迅速，其在图像处理、优化控制、人工智能和模式识别等领域发挥了重要的作用.在实际应用中需要神经网络具备一些动力学性质，由于放大器的开关速度是有限的，所以时滞在神经网络的运行过程中一定存在，因此探究时滞神经网络的动力学性质意义重大.同步性作为时滞神经网络的动力学行为之一，得到了广泛关注.文献[1-6]应用Lyapunov泛函、Kronecker积和矩阵理论等方法，提出了相应的同步控制策略，讨论了几类常时滞和变时滞神经网络的同步性，并给出了相应的同步判定准则.

近十年来，比例时滞神经网络的动力学受到国内外学者的广泛关注，并取得了一定的研究成果.文献[7-14]通过构建Lyapunov泛函和应用时滞微分不等式等方法，对比例时滞神经网络的全局渐近稳定性、指数稳定性和周期性等进行了研究，得到了相应的判定准则.比例时滞神经网络的同步性也得到了一些关注[15-17].文献[15]通过应用Lyapunov泛函研究一类比例时滞神经网络的同步性.文献[16]通过应用集值映射、微分包含理论和不等式技巧，给出了比例时滞神经网络同步性的条件.文献[17]针对一类递归神经网络首次提出了多项式同步的概念，并通过构造Lyapunov泛函和应用不等式技巧，设计合适的控制器，分别研究了以带比例时滞和不带比例时滞的神经网络作为驱动-响应系统的多项式同步性，并且揭示了指数同步性与多项式同步性之间的关系.

本文研究以比例时滞神经网络作为驱动-响应系统的多项式同步性.通过构造Lyapunov泛函和应用线性矩阵不等式的方法，得到了驱动-响应系统多项式同步性的充分条件，并通过数值算例及其仿真进行检验.

1 预备知识和模型

记E为单位矩阵，‖·‖为Euclidean范数.矩阵A>（<，≥，≤）0表示矩阵A正定（负定，半正定，半负定）.矩阵A的最小特征值和谱半径分别记为λmin（A）和ρ（A）.“*”表示矩阵中相应的对称部分.

考虑以如下比例时滞神经网络作为驱动系统

式（4）关于t求导得v˙i（t）=etx˙i（et），对于t≥t0，由式（1）可得

2 主要结果

定理1 假设（H1）和（H2）成立，且存在矩阵P>0，N>0，对角矩阵Y0>0，Y1>0，S>0，常数α>1，使得

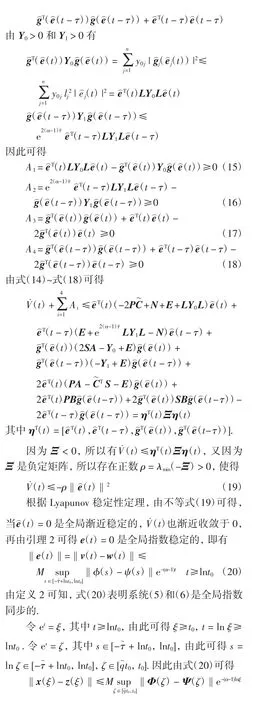
注1定理1通过证明系统（5）和（6）是全局指数同步的，来证明系统（1）和（2）是全局多项式同步的.

注2全局多项式同步和全局指数同步都是全局渐近同步，是其更明确、条件更强的细分情况，但两者的收敛速度不同，全局指数同步的收敛速度和收敛阶大于全局多项式同步.

注3文献[6]研究的是有界变时滞神经网络的同步性，本文研究的是无界时变的比例时滞神经网络的同步性，文献[6]的结果不能直接应用于本文模型.

定理2假设（H1）和（H2）成立，且存在矩阵P>0，N>0，对角矩阵Y0>0，Y1>0，H>0，常数α>1，使得

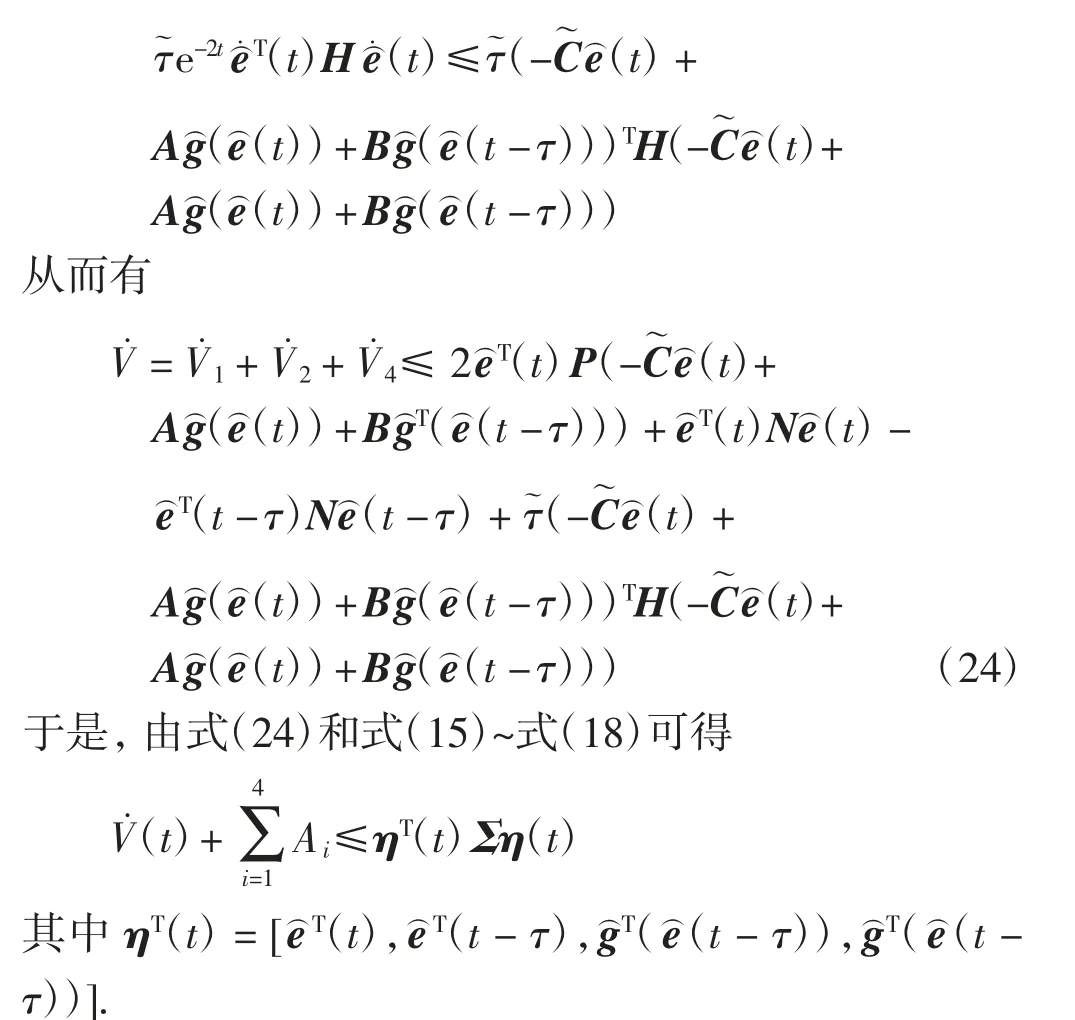
因为Σ<0，所以有V˙（t）≤ηT（t）Ση（t），又因为Σ是负定矩阵，所以存在正数ρ=λmin（-Σ）>0，使得V˙（t）≤-ρ‖（e（t）‖2.下面的证明过程与定理1类似，这里不再赘述.

注4定理1和定理2给出了2个保证驱动-响应系统同步性的判定准则，定理2的判定条件相较于定理1具有更强的时滞依赖性.定理1的判定矩阵中只有Ξ22项含有时滞，而定理2的判定矩阵中除Σ24外的非零项均含有时滞，在实际应用中可根据需求选取合适的判定准则.

注5本文给出了2个新的矩阵形式的同步性判定准则，矩阵形式的判定条件便于使用Matlab工具箱进行验证.

3 仿真研究

例 考虑比例时滞神经网络

系统（25）从（0，0）T初始的解轨迹的相图见图1，由图1可见，系统（25）是混沌的.

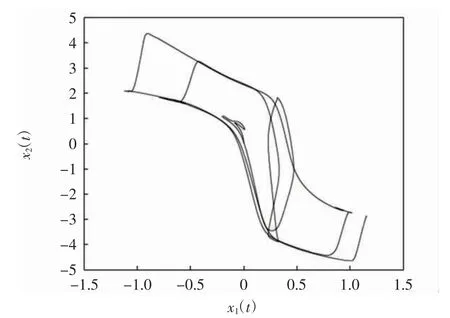
图1 系统（25）以（0，0）T为初值的相轨迹Fig.1 Phase trajectory of system（25）with（0，0）T as initial value

在无控制的条件下，系统（26）从（0.60，0.65）T初始的解轨迹的相图见图2，由图2可见，系统（26）也是混沌的.在有控制的条件下，系统（26）从（0.60，0.65）T初始的解轨迹的相图见图3，由图3可见，除初始部分外，系统（25）和（26）的相图基本一致.

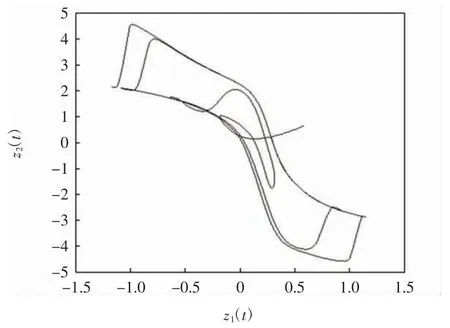
图2 系统（26）以（0.60，0.65）T为初值无控制的相轨迹Fig.2 Phase trajectory of system（26）with（0.60，0.65）T asinitial value without control

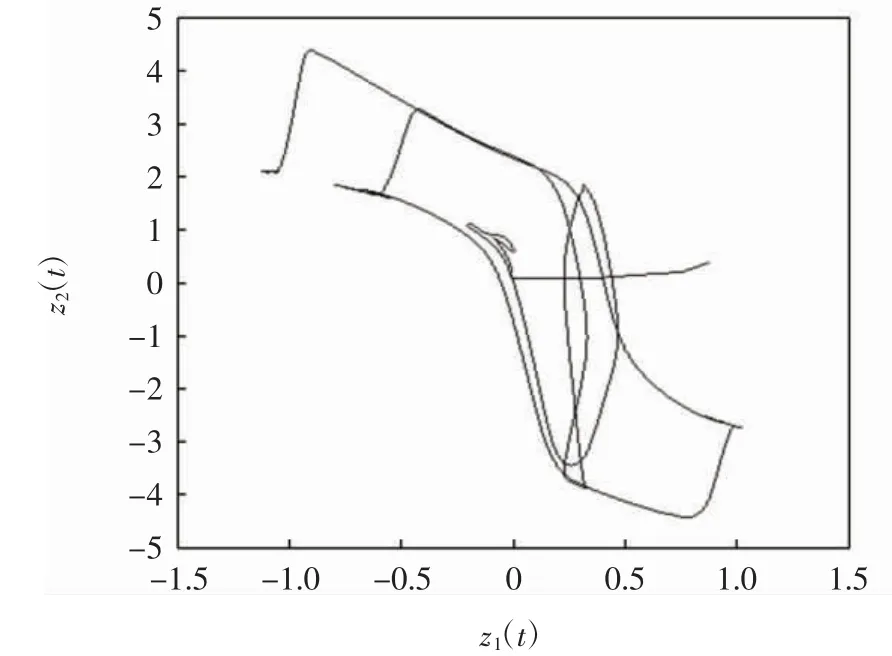
图3 系统（26）以（0.60，0.65）T为初值有控制的相轨迹Fig.3 Phase trajectory of system（26）with（0.60，0.65）T as initial value with control

使用Matlab工具箱，通过计算可得矩阵

同样，使用Matlab工具箱，通过计算可得矩阵使得Σ<0，因此定理2成立.

系统（25）的初始条件为（x1（s），x2（s））T=（0，0）T（0.1≤s≤1），系统（26）的初始条件为（z1（s），z2（s））T=（0.60，0.65）T（0.1≤s≤1），系统（25）和（26）同步性的时间响应曲线见图4，由图4可见，系统（25）和（26）实现了同步.取不同的初始条件，同步性的时间响应曲线见图5，由图5可见，系统（25）和（26）仍然是同步的.

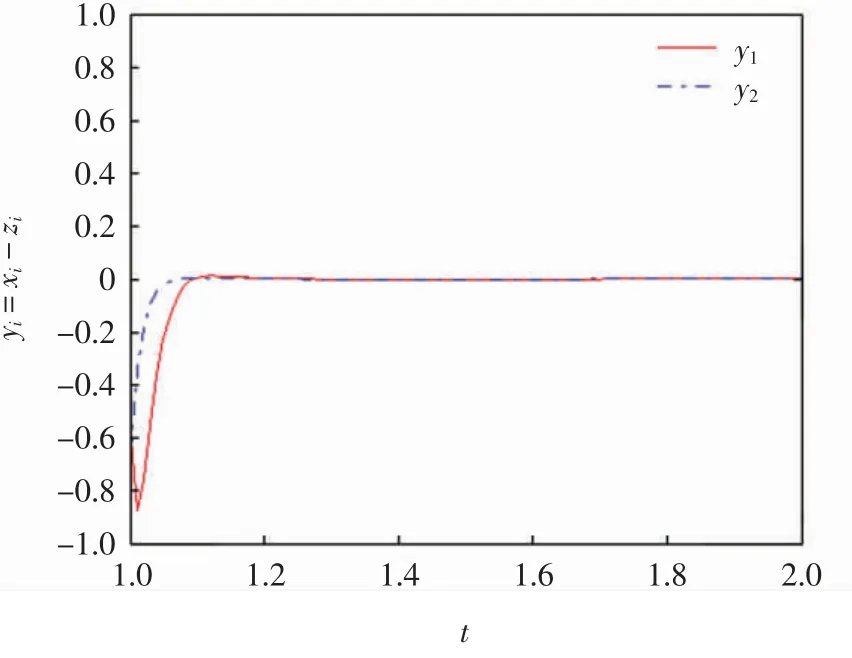
图4 系统（25）和（26）的时间响应曲线Fig.4 Time response curves of systems（25）and（26）

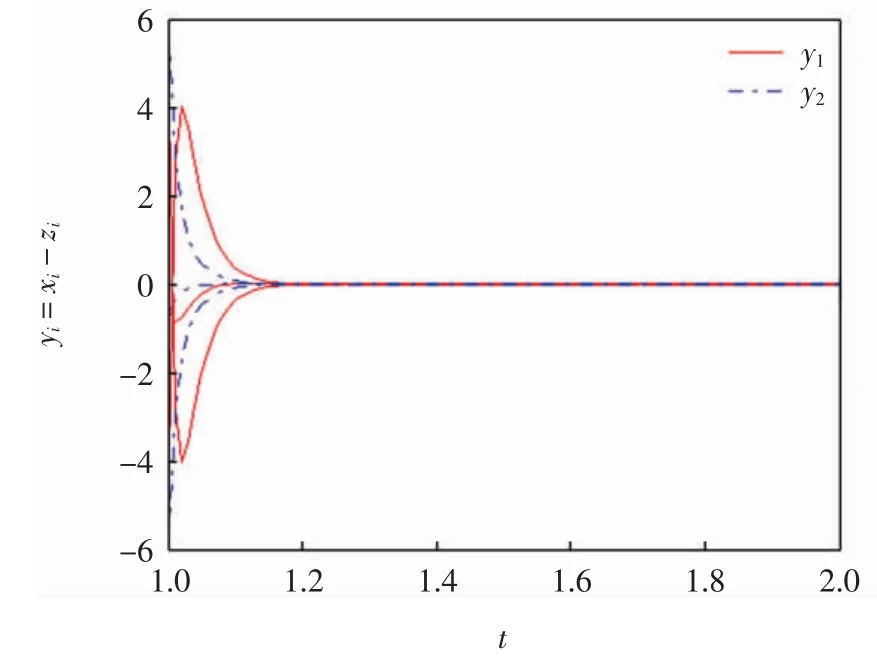
图5 多个初值下系统（25）和（26）的时间响应曲线Fig.5 Time response curves of systems（25）and（26）under multiple initial values

注6除时滞项外，本文算例的参数与文献[6]中的例1均一致，但文献[6]的结果不能直接应用于本文模型，本文模型是无界时滞的，具有更低的保守性.

注7在文献[15，17，19]中，控制器的设计非常精妙，但同时对控制器的要求也很高.与相同模型的文献[15]相比，本文对控制器的约束条件更弱，因此本文结果更具一般性，在实际应用中具有更低的保守性.

4 结语

本文应用Lyapunov稳定性理论和线性矩阵不等式的方法分析了以比例时滞神经网络作为驱动-响应系统的全局多项式同步性，得到新的保证驱动-响应系统多项式同步的判定条件，并通过数值算例及其仿真进行检验，判定条件易于应用Matlab工具箱进行验证.下一步工作是实现比例时滞神经网络的同步性在保密通信中的应用.