基于正态变换的玛纳斯河水文频率研究
蔡国涛 乔长录
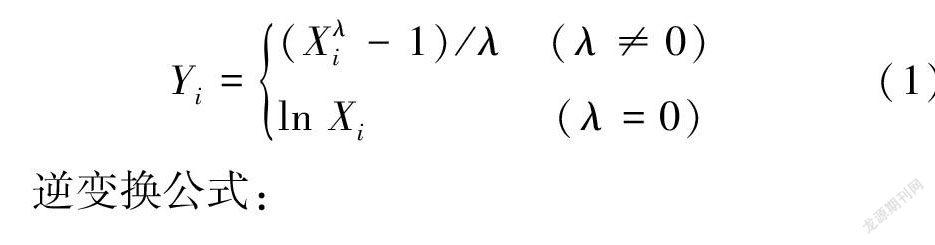


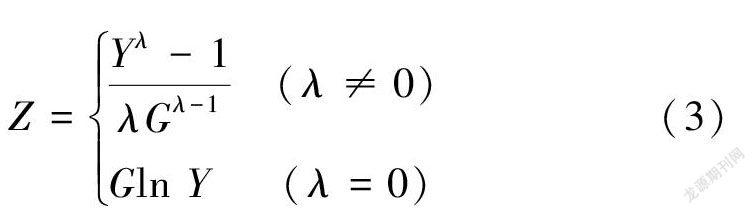
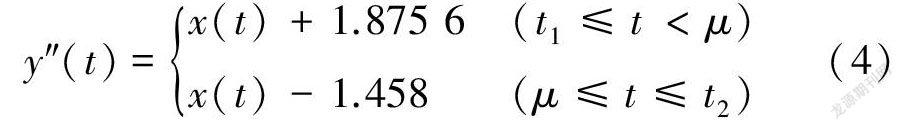
关键词:正态变换;水文频率计算;适线法;非一致性修正;玛纳斯河
中图分类号:P333.9 文献标志码:A doi:10.3969/j.issn.1000-1379.2022.03.005
引用格式:蔡国涛,乔长录.基于正态变换的玛纳斯河水文频率研究[J].人民黄河,2022,44(3):21-25,31.
1引言
水文频率计算是综合运用水文学、水文统计学和概率统计学等原理,利用研究区多年实测水文数据对水文事件的规律进行统计分析,定量表征水文变量设计值与设计标准(频率或重现期)之间的关系,是各类涉水工程规划、设计、确定工程规模和管理决策的主要依据[1]。水文频率计算经过一百多年的研究和发展,形成了较为完整的理论体系和方法。目前水文频率计算通常有参数方法和非参数方法两种:参数方法需要先假定样本总体的分布形式,然后通过总体分布来计算待估参数,最后根据总体分布函数推求水文变量设计值;相反,非参数方法可以直接根据样本信息估计水文变量的设计值,不必假设总体分布形式[1]。水文频率计算也可先对样本进行正态化转换,根据转换后的样本估计指定频率设计值,再进行反变换推求原始变量总体设计值[2-3]。Chen等[4]和徐炜等[5]在正态变换研究中指出,单变量正态变换过程中,原偏态分布到正态分布是一对一单调递增的关系,利用正态变换方法得到的序列能较完整地保留原偏态分布的样本信息。国内很多学者将Box-Cox变换应用于水文领域,但是基于Johnson变换的研究甚少。所以,笔者通过Box-Cox变换和Johnson变换两种正态变换方法对玛纳斯河年径流量序列进行正态变换,通过对比分析正态性检验结果和水文频率计算结果,最终确定两种正态变换方法的优越性和稳健性,以期为我国干旱区水资源规划和工程规划设计应用该方法提供参考。
2正态变换方法
2.1Box-Cox变换
Box-Cox变换是Box和Cox在1964年提出的一种可以明显改善数据正态性的广义幂变换方法,其函数关系式如下[6]:
2.3参数估计
常用的参数估计方法有矩法、最小二乘法、极大似然法、贝叶斯法、适线法、权函数法和概率权重矩法等。在水文频率计算中,P-Ⅲ型分布参数采用适线法估计。Johnson变换中,待估参数计算采用Chou等[9]提出的方法。Box-Cox变换中,采用最小化待变换数据的标准差(介于-5和5之间),为了准确比较不同λ值的标准差,使用以下公式计算标准化的变换值Z[10]。
式中:G为原始数据的几何均值;Y为待变换数据。
3水文变量非一致性检验及修正
在计算水文变量频率时,要求水文资料具有一致性,即随机变量独立且总体分布相同。但是近些年大规模的人类活动(修建水利工程等)和显著的气候变化,直接或间接地改变了流域的下垫面状况,最终导致流域水文要素失去了一致性特点。如果水文序列中有趋势和跳跃成分,序列的一致性将会被破坏,在水文频率计算之前,要对水文资料进行非一致性检验及处理。因此,需要对水文资料进行趋势分析和变异检测,并根据检验结果对非一致性成分进行剔除。
3.1非一致性检验方法
常用的非一致性检验方法有:Mann-Kendall秩次检验法、斯波曼(Spearman)秩次相关检验法、有序聚类法、秩和检验法、游程检验法、T检验法、F检验法、线性趋势的相关系数检验法、小波分析法、信息熵分析法等[11-13]。本研究基于Matlab软件选用Mann-Kendall(M-K)秩次检验法,并且使用趋势分析和游程检验对水文序列进行非一致性检验。
3.2非一致性修正方法
非一致性修正方法主要有基于還原/还现、基于非一致性极值序列直接进行水文频率分析计算等[14]。本文采用胡义明等提出的修正方法,趋势修正即假定“在具有趋势变化的实测序列中存在一个理想的平稳(一致性)状态,平稳状态的振动中心(平均值)是序列分割点前后两个实测样本序列平均值的线性组合”。通过综合分割点前后两段序列,进行序列趋势性变异的一致性修正[15]。跳跃变异修正的假定与趋势修正相似,最终通过综合跳跃变异点前后序列的均值进行整体序列的修正[11]。
4应用研究
以玛纳斯河肯斯瓦特水文站1955—2010年共56a实测年径流量为原始数据序列,首先对年径流量序列进行变异检验,然后通过上述非一致性修正方法对变异序列进行修正。使用两种正态变换方法对年径流量序列进行正态转换并检验其正态性,最后基于两种反变换方法并对比适线法进行水文频率计算和综合分析。
4.1研究区概况玛纳斯河流域位于新疆天山北麓准噶尔盆地南部,发源于天山北坡的依边哈比尔尕山,位于东经84°47′—85°31′、北纬43°27′—45°30′之间,流域远离海洋,位于欧亚大陆腹地,气候干燥,属典型的大陆性干旱气候区[16]。肯斯瓦特水文站是玛纳斯河上的一个控制测站,测站断面基本上控制了玛纳斯河全部的地表径流。该站始建于1955年5月,控制流域面积约4637km,多年平均年径流量约为12.21亿m。
4.2非一致性检验及修正
4.2.1跳跃变异检验及修正
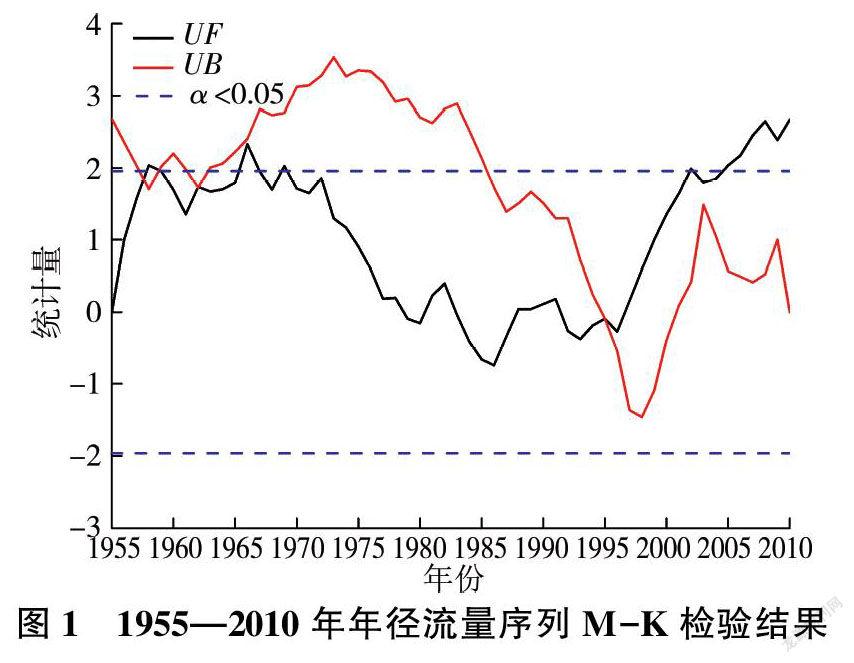
对年径流量序列进行M-K检验,结果如图1所示。
由于1955—2010年年径流量序列M-K检验图中UF与UB交点位置和历史文献资料初步确定变异点在1995年附近,经有序聚类分析法和滑动T检验法进一步确定跳跃变异年份为1996年。以1996年为分割点将整个年径流量序列分为前后两个子序列,权重系数为0.44。跳跃变异修正公式为
式中:μ=1996;t=1955;t=2010;x(t)为原实测序列。
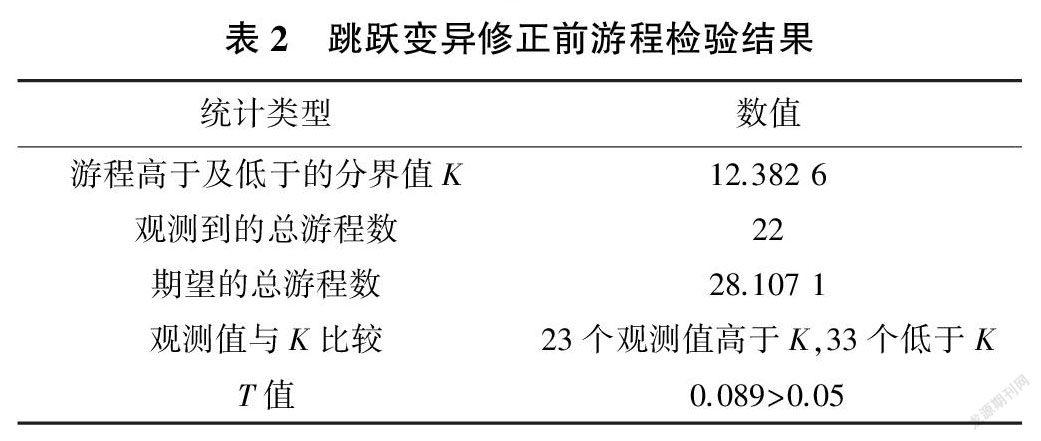
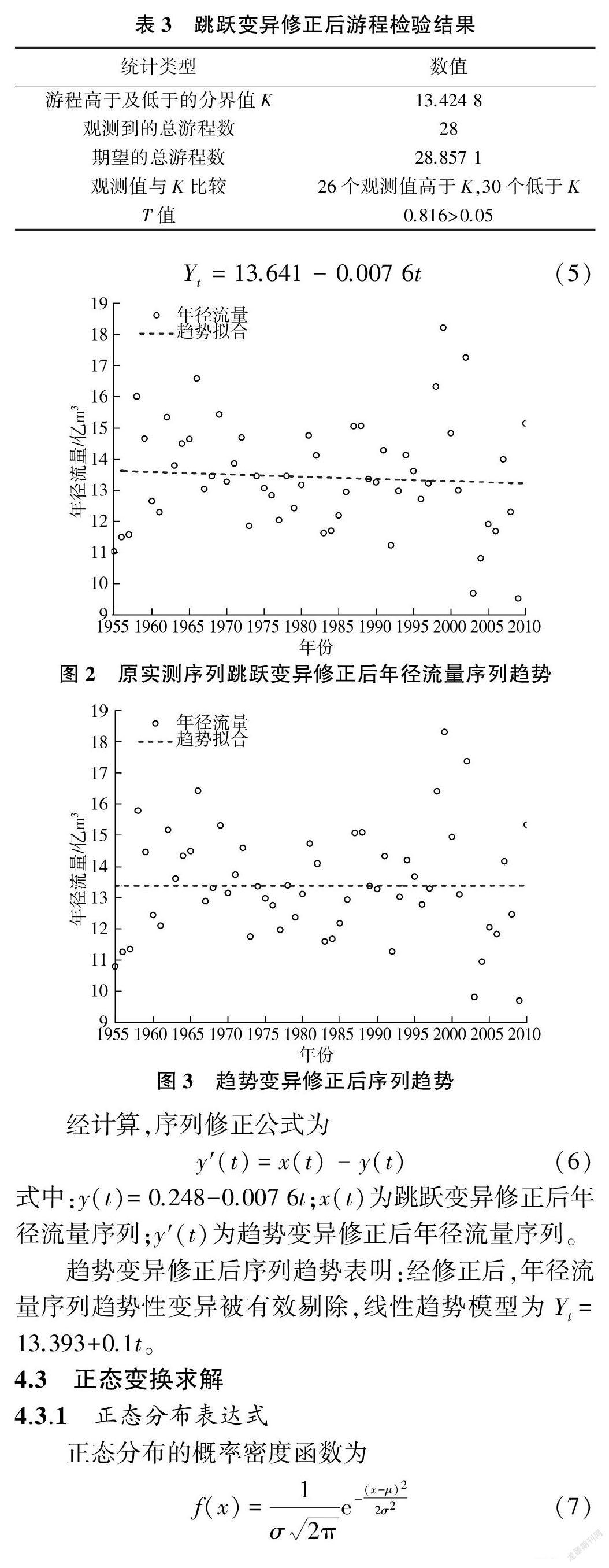
对跳跃性变异修正前后的年径流量序列进行游程检验,结果见表2和表3。由游程检验结果可知,跳跃变异修正前,游程数量偏少且检验统计量T值(为0.089)略大于0.05,表明序列随机性较差,存在跳跃变异。经跳跃变异修正后,T值(为0.816)远大于临界值0.05,且游程数量适中,表明序列具有独立性、随机性,即跳跃性变异被有效剔除。
4.2.2趋势变异检验及修正
图2为原实测序列跳跃变异修正后年径流量序列的趋势分析,结果表明序列存在明显下降趋势。图3为趋势变异修正后序列的趋势分析。年径流量序列线性趋势模型为经计算,序列修正公式为
式中:y(t)=0.248-0.0076t;x(t)为跳跃变异修正后年径流量序列;y′(t)为趋势变异修正后年径流量序列。
趋势变异修正后序列趋势表明:经修正后,年径流量序列趋势性变异被有效剔除,线性趋势模型为Y=13.393+0.1t。
4.3正态变换求解
4.3.1正态分布表达式
正态分布的概率密度函数为
式中:μ为位置参数(均值);σ为尺度参数(标准差)。式(7)记作X~N(μ,σ)。
当μ=0,σ=1时,正态分布就成为标准正态分布:
4.3.2正态性检验
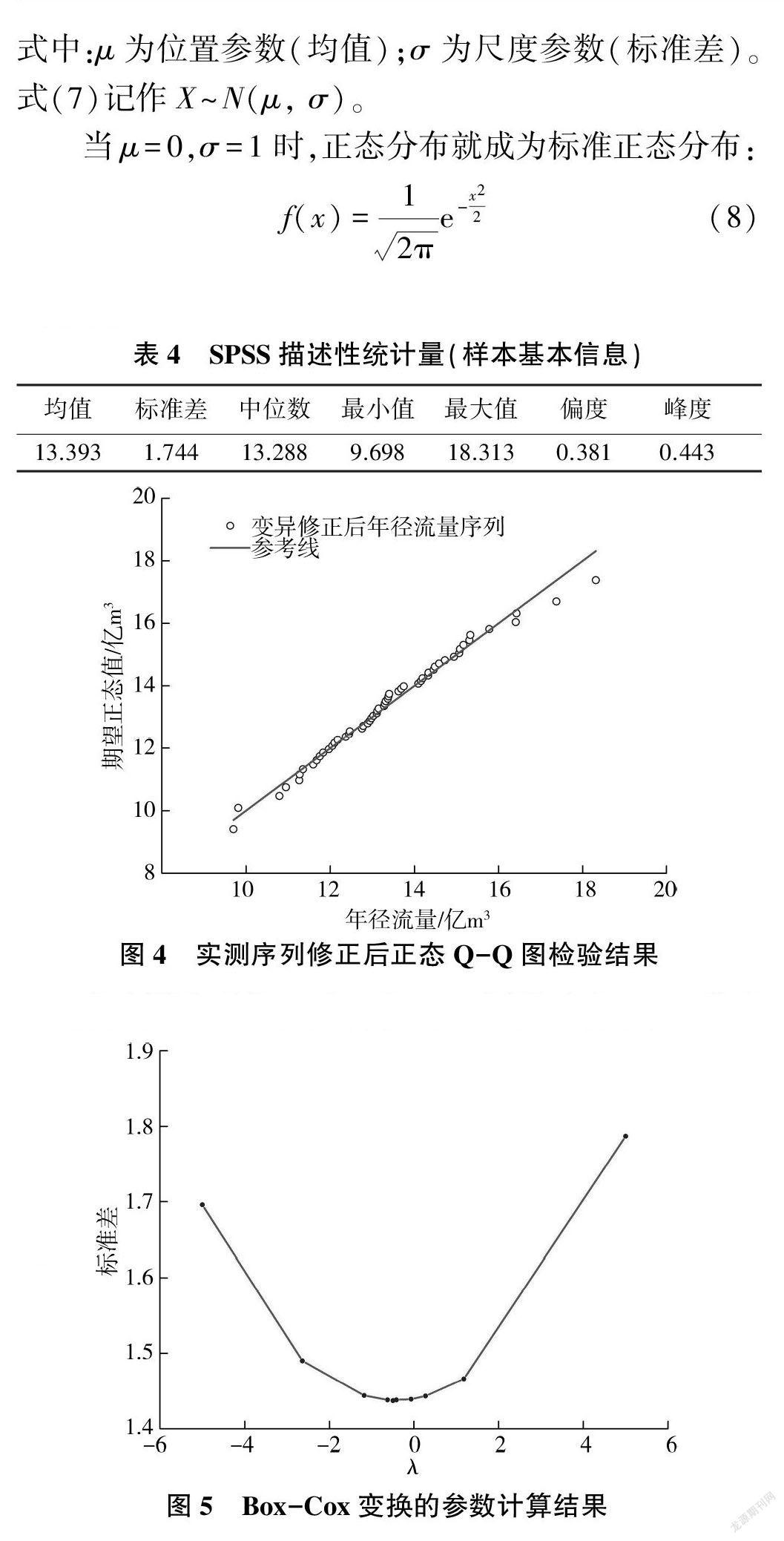
首先对变异修正后水文序列进行正态性检验,常用的正态性检验方法有图示法、峰度检验法、非参数检验法。图示法包括P-P图、Q-Q图、直方图、箱线图、茎叶图等。非参数检验方法包括Kolmogorov-Smirnov检验、Lilliefor检验、Shapiro-Wilk(W检验)等。本文借助统计学常用软件SPSS和Q-Q图进行正态性检验。SPSS检验结果见表4,正态Q-Q图检验结果如图4所示。
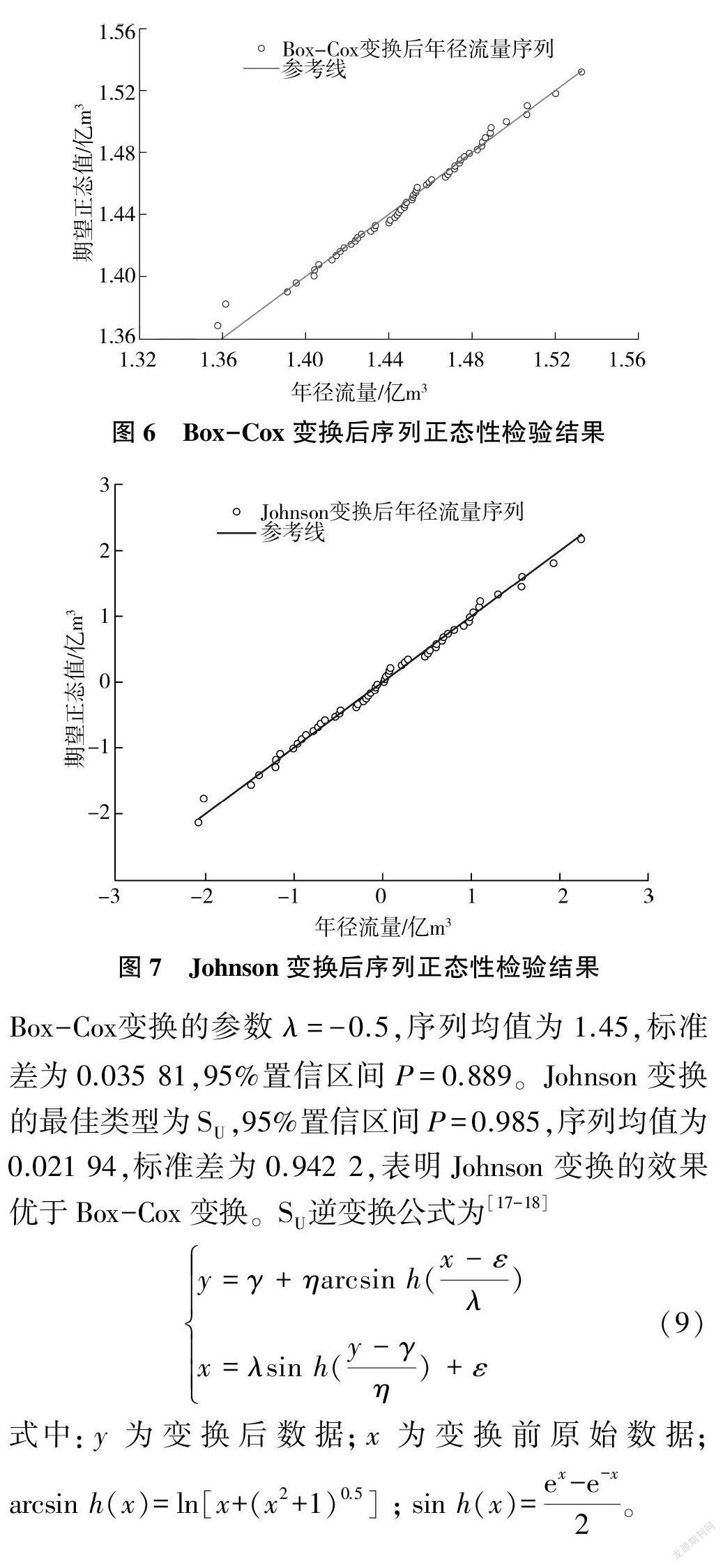
由实测序列修正后正态Q-Q图检验和SPSS描述性统计量可知,水文序列不服从正态分布。样本偏度为0.381,峰度为0.443,所以需要对序列进行正态变换。分别使用Box-Cox和Johnson变换对年径流量进行正态变换,Box-Cox变换的参数计算结果和两种变换后序列的正态性检验结果如图5~图7所示。
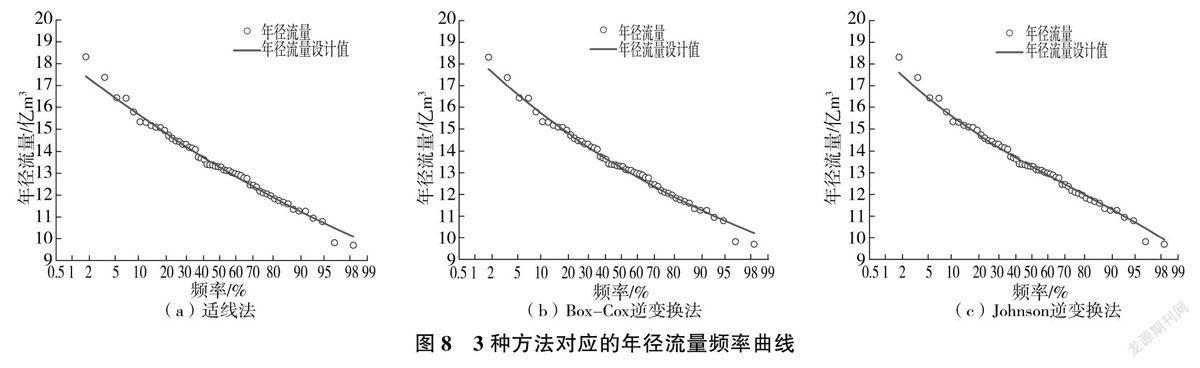
根据Box-Cox变换和Johnson变换结果可知,Box-Cox变换的参数λ=-0.5,序列均值为1.45,标准差为0.03581,95%置信区间P=0.889。Johnson变换的最佳类型为S,95%置信区间P=0.985,序列均值为0.02194,标准差为0.9422,表明Johnson变换的效果优于Box-Cox变换。S逆变换公式为[17-18]
5年徑流量频率计算
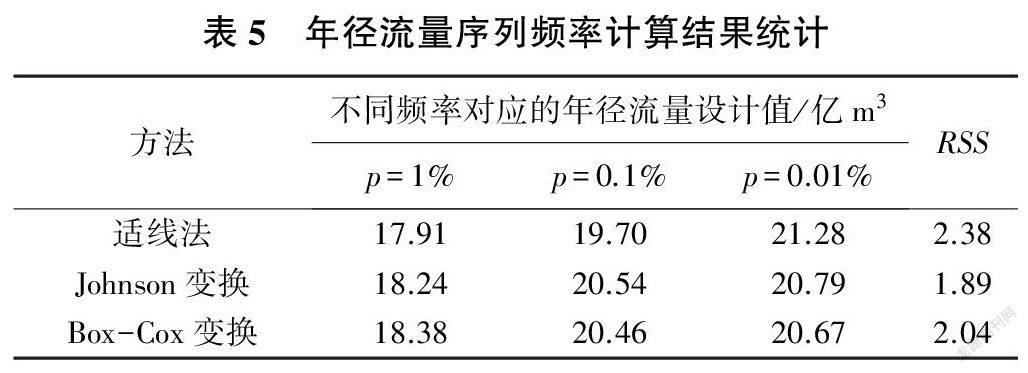
对实测序列修正后进行水文频率计算,水文频率计算采用适线法[19]。实测序列修正后基于Box-Cox变换和Johnson变换进行指定频率下年径流量设计值计算,计算方法采用正态逆变换[20]。3种方法对应的年径流量频率计算结果如图8所示。
由年径流量序列频率计算结果可知,基于Johnson变换推求的年径流量设计值和经验频率拟合度较高,其次是基于Box-Cox变换推求的,最后是基于适线法推求的。Box-Cox逆变换推求的年径流量设计值与原实测水文序列的高水端拟合度较高,Johnson逆变换推求的年径流量设计值与原实测水文序列整体和低水端拟合度较高,适线法计算的年径流量设计值与原实测水文序列的中水端拟合度较高。原因是:经过Box-Cox变换的序列通过了正态性检验且与Johnson变换相比较低,但是因为其变换只有一个待估参数,所以当逆变换序列发生很小的变化时,变换后的结果也会有大的波动,导致在水文序列高水端不稳定时的拟合更有优势,从而可以较精确进行水文频率计算。Johnson变换有多个形式和变换参数,正变换与逆变换之间的稳健性比Box-Cox变换好,水文变量发生大的波动时,逆变换的设计值依然比较稳定,和实测年径流量序列整体拟合度较高,但与高水端拟合度稍劣于Box-Cox变换。因此当应用Box-Cox变换和Johnson变换推求指定频率的水文变量设计值时,需要依据河流自身水文特性综合利用两种方法。
利用残差平方和RSS衡量设计值和实测值的拟合程度:一组数据的残差平方和越小,表示其拟合程度越高。残差平方和计算结果和3种水文频率计算方法对应不同频率年径流量设计值见表5。
相比于实测年径流量序列修正后基于适线法计算结果,基于Johnson变换推求百年一遇、千年一遇的年径流量设计值偏大,万年一遇的年径流量设计值偏小;基于Box-Cox变换推求的年径流量设计值与Johnson变换相差不大。
6结语
基于正态变换和逆变换原理,采用Box-Cox变换和Johnson变换对新疆干旱区玛纳斯河进行水文频率计算研究,通过逆变换推求指定频率下对应的年径流量设计值。实测序列修正后以P-Ⅲ型分布曲线为水文频率计算线型,采用优化适线法推求不同频率对应的年径流量设计值。并对结果进行对比分析,主要得出了以下结论。
(1)由年径流量序列频率计算结果可知,基于Johnson变换推求的年径流量设计值和经验频率拟合度较高,其次是基于Box-Cox变换推求的,最后是基于适线法推求的。Box-Cox逆变换推求的年径流量设计值与原实测水文序列的高水端拟合度较高,Johnson反变换推求的年径流量设计值与原实测水文序列整体和低水端拟合度较高,适线法计算的年径流量设计值与原实测水文序列的中水端拟合度较高。
(2)相比于原实测修正后年径流量序列基于适线法计算结果,基于Johnson变换推求百年一遇、千年一遇的年径流量设计值偏高,万年一遇的年径流量设计值偏低,基于Box-Cox变换推求的年径流量设计值与Johnson变换相差不大。
【责任编辑 张帅】

