基于自适应细化网格的初期血栓形成计算模型

边朔，马朝青,2

1. 烟台大学 计算机与控制工程学院，山东 烟台 264005

2. 高端海洋工程装备智能技术烟台市重点实验室，山东 烟台 264005

血栓是活体血管系统中凝血物质和血细胞形成的凝块，会造成组织缺血性坏死，从而影响器官功能，甚至危及生命。数据表明，急性心肌梗塞、缺血性中风、肺栓塞和弥散性血管内凝血等血栓性疾病导致的死亡人数逐年增高[1]。血栓形成是临床各科疾病中常见的一种病理过程，可见于心房室腔、动脉、静脉和微血管。血栓的形成机制已通过多年的研究[2-4]获得了基本认识。19 世纪中期，Virchow 提出了血栓形成病理生理机制的三要素：血流缓慢、血管破损和血液高凝状态[5]。在20 世纪80 年代之前，针对血栓的研究主要依靠在活体内和活体外进行的动物实验以及实验室仪器实验。通过研究者的实验确定了导致血栓形成的大多数复杂生物反应级联[6-8]。随着对血栓形成机制研究的不断地深入，一系列描述凝血过程及其子过程的数学模型被提出。随着计算机技术的迅速发展，国内外研究者对血栓形成机制的建模更倾向使用计算机模拟实验研究血栓形成的机理，这一类研究的核心是建立血栓形成的计算模型。

国内外研究者根据模型中血栓形成物质的描述方式将计算模型分为3 类：连续模型，离散粒子模型和混合模型。连续模型[9-13]中血管、血流、血细胞以及凝血因子等物质均描述为连续介质，模型以偏微分方程的组合为主。与连续模型相反，离散粒子模型[14-20]将所有物质描述为细微粒子，模型以粒子移动和相互作用为主。混合模型[21-23]中的凝血物质和血小板等血细胞描述为离散粒子，血液和血管描述为连续物质。因此，相比单纯的连续模型和离散模型，在计算复杂度和跟踪粒子行为方面具有更好的性能[24-25]。为了能够描述较为复杂的血栓形态和获得更平滑的血栓表面，与之前混合模型中用粒子簇对血栓进行建模不同，Ma 等[26]的研究中将血栓描述为具有可移动自由表面的连续体，并基于水平集方法建立模型。

虽然水平集方法对追踪移动过程中拓扑结构发生改变的轮廓非常有效，但对模型空间高一维的描述和偏微分方程的求解增加了模型的计算复杂度。文献[27]提出一种用于研究动态变化过程中界面演化的算法，该算法基于水平集方法，使用窄带和快速行进的方法应用于动态自适应网格，并结合了四叉树等数据结构。这种方法将主要的计算精力集中放在重要的区域上，节约大量的计算资源。文献[28]提出了一种基于三维自适应网格生成方法的局部细化技术，根据几何特征有效地进行局部细化，网格细化质量和灵活性得到显著提高。

本文对血栓混合模型的建模网格进行了优化，将窄带法与局部细化相结合，提出针对可移动界面的自适应细化网格，在保证计算准确率的基础上减少数据量。同时，在血栓生长模型中引入正则化水平集演化（distance regularized level set evolution，DRLSE）方法[29]，有效降低水平集方程求解过程中的计算量。利用该模型对以血小板为主的血栓的形成过程进行更高效的仿真，分析血流和血管形状对初期血栓形成的影响。

1 水平集方法中的自适应网格细化

水平集是计算流体力学中常用到的一个重要概念。1988 年，Oshe 等[30]首次提出了水平集方法，有效解决了曲面演化问题的数值方法，并适用于任意维数空间。水平集方法的主要思想是将n维曲面的演化问题在n+1 维空间中解决，即将界面嵌入到一个超曲面中，并求解表示曲面演化的隐式水平集函数方程式。水平集方程主要包括3 个要素：超曲面的数据表示、控制曲面演化的一系列偏微分方程以及相应的数值解法。

首先使用符号距离公式（signed distance function,SDF）建立表示超曲面的水平集函数：

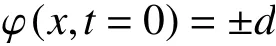
式中：d是点x到曲面最近点的欧式距离，其符号取决于点x位于曲面的内部还是外部，通常情况下定义内部为负号，外部为正号。

水平集函数的演化遵守式(1)：

式中：F是曲线上各点的演化速度，方向为曲线的法线方向。已知初始水平集 φt=0，通过式(1)可以求得水平集函数在速度F的作用下经过一个时间步长 Δt后的取值。

在迭代求水平集函数数值解的过程中涉及的偏微分方程求解，不论是使用低精度的迎风（upwind）差分法，还是高精度的龙格库塔（Runge-Kutta）方法，都会产生较大的计算量，限制水平集方法在各领域的应用。

在水平集方法的各应用领域中，速度F通常仅定义在零水平集上。但水平集函数是在整个计算空间上进行更新的，因此需要将F也扩展到整个空间。这使得原始水平集方法在求解大迟钝轮廓时计算量大且效率低下。考虑到在某一时间点上水平集函数的一系列取值中零水平集只有一个，并且被关注的也只有零水平集所代表的曲面，因此可以采用窄带算法[31]仅求取零水平附近的函数值来降低计算量。窄带方法首先在轮廓的内部和外部分别设定宽度为 θ的带状区域，形成一个带宽为 2θ的窄带围绕零水平集，如图1(a)。在对水平集函数进行求解时，只需要将速度方程扩张至窄带边界，并且仅对窄带内部的网格进行水平集更新。

利用水平集方法追踪运动界面时，界面精度和质量损失都与网格的分辨率有关。如果所有网格都进行细化，则计算时间和存储空间将大大增加。因此，本文采用自适应网格技术对窄带区域网格进行细化，对远离界面区域的网格进行粗化处理，以确保界面附近的网格具有更高的分辨率，提高网格的计算精度。假设窄带的带宽为 2θ，如果网格上水平集的值满足 |φ|≤θ，则需要进行细化（图1(b)）。

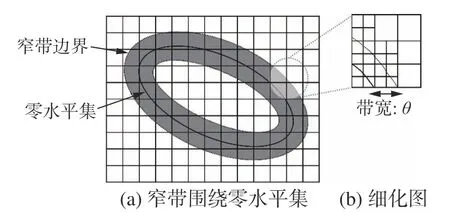
图1 窄带示意

在窄带法中，窄带内的网格被存储压缩为一维数组。但水平集在演化过程中，不仅窄带会定期更新，窄带内网格中水平集数据也频繁地被调取和更新。细化后的笛卡尔网格在数据存储和查找上更为复杂，因此不能继续使用原始的压缩矩阵形式存储细化数据。针对三维笛卡尔细化网格，八叉树结构更容易管理网格数据，提高计算和存储效率。

2 初期血栓计算模型

本文针对初期血栓形成过程建立particle-continuum 混合模型。初期血栓常见于动脉或血流速度较快的静脉，是在血栓形成初期由大量血小板和少量纤维蛋白组成的小节状或赘生物状凝块，也称为血小板血栓或白色血栓。因此，本模型包含的主要元素有拟设有破损内壁的血管、血管性血友病因子（von Willebrand Factor，vWF）、血浆、血小板和初期血栓。在混合模型中，血管、vWF、血浆和血栓属于连续介质（continuum），为了能够观察血小板在血栓形成过程中的运动行为，利用离散颗粒（particle）模拟血小板。图2 是模型的三维示意图，模型中的血管被定义为单入口单出口的通道，血浆充满整条血管并从入口流向出口。在血管中段预设小区域的血管内膜破损和血管狭窄。破损后暴露出的皮下胶原纤维引发凝血机制，由血浆从血管入口带入的血小板会在vFW 的作用下黏附在破损内膜处，并引发更多的血小板聚集，逐步生长为初期血栓。

图2 带有破损血管壁的初期血栓生长三维模型示意

根据模型中包含的元素，计算模型被分为4 个子模块：血浆模型、vWF 模型、血小板模型和血栓模型。血浆模块对血管中的血浆流动进行建模，该模块为整个模型提供血液动力学环境。vWF 模块对vWF 因子的对血小板的影响进行判断，其释放和扩散情况受血浆模块提供的速度场影响，该模块中的vWF 因子将诱导血小板激活。血小板模块对血小板的移动进行建模，血小板的移动受血浆的速度场和vWF 的共同影响。血栓模块对血栓的生长进行建模，组成血栓的血小板由血小板模块提供。

2.1 血浆模块

在该模块中，本文假设血浆为不可压缩的粘性牛顿液体。将引入Navier-Stokes（N-S）方程[17]作为血浆的速度函数：

通过对N-S 方程的分步求解可获得血管内的血浆速度场，并将其同时用于vWF 模块、血小板模块和血栓模块。

2.2 vWF 模块

vWF 是参与初期血栓形成的主要凝血因子之一，主要由内皮细胞合成分泌后存在于血浆中，内皮细胞在受刺激或损伤后，血浆内局部vWF 浓度会提高，导致血栓形成。vWF 在初期血栓形成中主要参与血小板的黏附和聚集过程。首先，vWF与血小板膜糖蛋白GPIⅠb-Ⅸ复合物结合，引导血小板降低移动速度并黏附于血管壁损伤部位形成血小板覆盖；然后与GPⅡb-Ⅲa 结合，诱导血小板聚集，进一步扩大血小板血栓的体积。vWF 对血小板的作用受血液剪切速率影响，其与GPIⅠb-Ⅸ的结合在剪切速率大于1 000-1时发生、与GPⅡb-Ⅲa的作用在剪切速率1 000-1～10 000-1发生[31]。

在本模块中，根据局部的剪切率确定vWF 因子是否对血小板产生作用以及产生何种作用。使用血浆模块计算得出的血浆流速u可计算血管内血流的剪切速率：

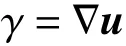
当血小板所在位置剪切速率大于阈值γact=1 000-1时，血小板被激活，继而发生黏附和聚集反应；当剪切速率大于阈值γno-ag=10 000-1时，仅产生黏附作用。由于vWF 因子的浓度在破损内膜处最高，设定血小板所受vWF 的影响程度随血小板与破损内膜距离的增大线性递减。

2.3 血小板模块

根据初期血栓形成过程中血小板在vWF 影响下产生的黏附和聚集作用，定义2 种血小板状态：静息状态和激活状态；以及3 种作用于血小板上的力：血浆拖拽力、黏附诱导力和聚集诱导力。

正常状态下，血小板为静息状态，仅在血浆拖拽力作用下随血流移动，血浆拖拽力计算方式为

式中：Fad_max、Fag_max分别为黏附力和聚集力的最大值；Dad、Dag分别为血小板中心与破损内膜和血栓表面的最近距离；nad、nag分别为从血小板指向破损内膜和血栓表面最近点的法向量，用于确定受力方向。考虑vWF 浓度随与破损区域的距离增大而减小，诱导力的大小和血小板与破损内膜或血栓表面的距离成反比。

2.4 血栓模块

血小板在黏附和聚集的过程会被激活并融合到血栓中。由于模型中血小板属于颗粒，血栓属于连续介质，融合过程是从离散颗粒到连续介质的转化的过程。血栓模块主要利用水平集方法，完成这一过程中的转化，实现血栓的生长。同时，为了提高水平集方法的计算效率，水平集的定义及水平集方程的求解引入了自适应细化网格方法。

首先，与血液、血管壁和血栓均使用基于符号距离公式的水平集函数 φ描述:

发生黏附或聚集的血小板融入血栓时，血栓的表面将向血浆一侧扩张。本文定义血栓表面的变化分为2 个步骤，首先按血小板形状扩张表面，然后用小幅度的曲率速度平滑血小板与原表面的连接边缘。为了在扩张过程使水平集保持符号距离公式的形式，本文引入DRLSE。在第一步的扩张中，使用该方法代替Fast Matching Method 高效地初始化水平集；第二步的平滑化中加入正则项，在水平集方程求解过程中省略多次再初始化步骤。DRLSE 的水平集演化方程为

3 仿真实验结果与分析

3.1 狭窄血管内的仿真实验

血管狭窄是导致血栓形成的重要原因之一，本文应用提出的初期血栓形成模型中建立具有局部狭窄的动脉血管3D 模型，对初期动脉血栓的形成过程进行了仿真，并分别对狭窄程度和破损位置对血栓的生长速度和几何形态的影响进行分析。

仿真实验中的血管设定是直径为 4 mm的颈动脉，血流速度为1 m/s。实验分别在管状直血管和有局部狭窄的血管中进行，血管狭窄设定为动物实验中通常使用的针尖压迫血管产生的局部狭窄。为了模拟这一过程，在对血管进行3D 形态建模时，利用二维高斯方程获得血管壁的峰状突起，通过调整高斯方程的系数控制突起的高度和范围。图3 为实验中使用的2 种狭窄血管，最狭窄处分别占血管半径25%和50%，黄色为血管突起区域。

图3 仿针使用的2 种狭窄血管

首先，设定全部突起部分存在血管内壁破损，图4 为狭窄程度为25%时血栓形成过程仿真图，黄色区域为血管破损区域及破损上形成的初期血栓。图5(a)为血管无狭窄和25%狭窄时破损出现0.3 s 后血栓内血小板的数量。结合图4可见，无狭窄情况下狭窄出口和入口处血栓生长程度相似，狭窄使生长速度上升且出口处速度高于入口出速度。E. Westein 等[33]通过动物实验证明了血管出现狭窄后的血流状态改变会导致受vWF 主导的血栓生长速度加快，并且血小板在凸起后半段的聚集速度大于前半段，如图5(b)所示。图5 中，本文仿真结果（图5(a)）与该实验结果（图5(b)）一致，可验证本文模型的有效性。

图4 25%狭窄下的血栓形成，黄色区域中突起为血栓

图5 无狭窄和有狭窄下同一时间内血栓内包含血小板数量

图6 为血管狭窄程度为25%的情况下，破损出现在不同位置时初期血栓的形成过程。当破损区域在狭窄上游时，初期血栓中血小板多聚集于血流入口处，因为该区域具有率先影响和捕获血小板的位置优势。当破损区域位于狭窄入口和出口时，狭窄促使顶端处出现明显的聚集。但是当破损出现在下游时，血小板反而在血流出口方向聚集。

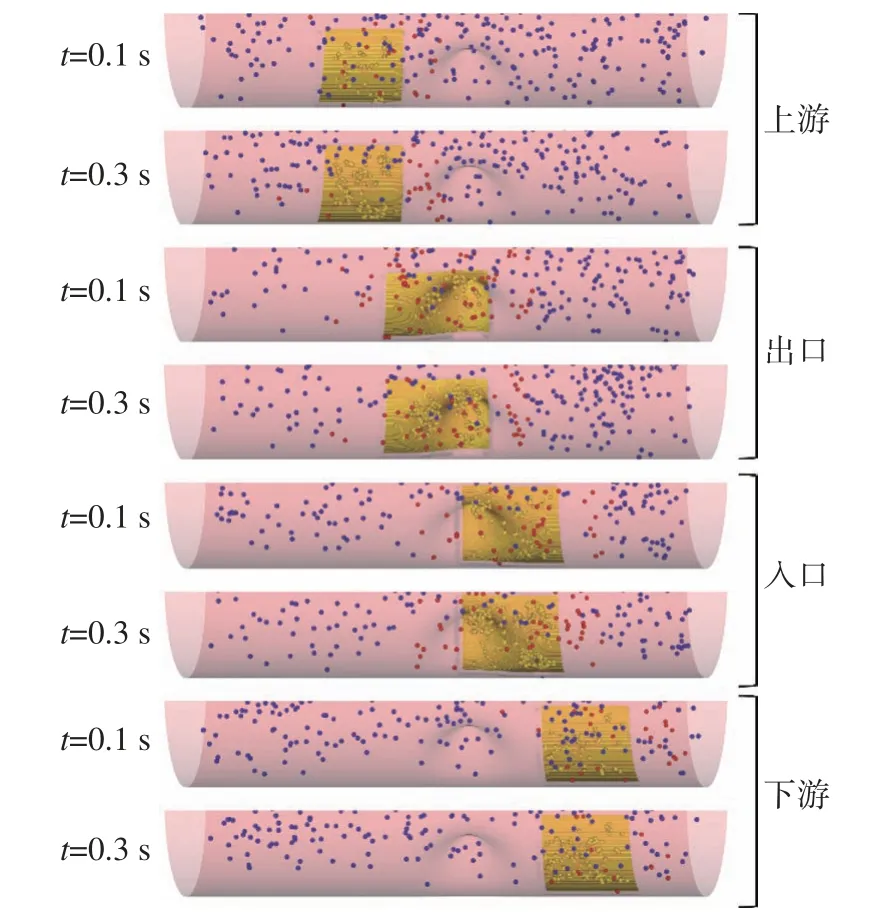
图6 不同血管内壁破损位置的血栓形成过程

本文在25%和50%狭窄的血管中，分别对破损区域出现在狭窄上游、入口、出口和下游这4 种条件下进行了10 次血栓形成仿真实验，获得了血栓在0.5 s 内的生长情况并绘制图7。如图7所示，血管狭窄程度增大会促进血栓形成，且狭窄出口处的形成速度大于狭窄入口处，这与之前实验结果（图5(a)）和文献[33]中的实验结果（图5(b)）一致。结合前文分析的血小板聚集区域，由于当破损在出口时，更多的血小板聚集在狭窄的顶峰区域，该情况下更容易造成血管的堵塞。

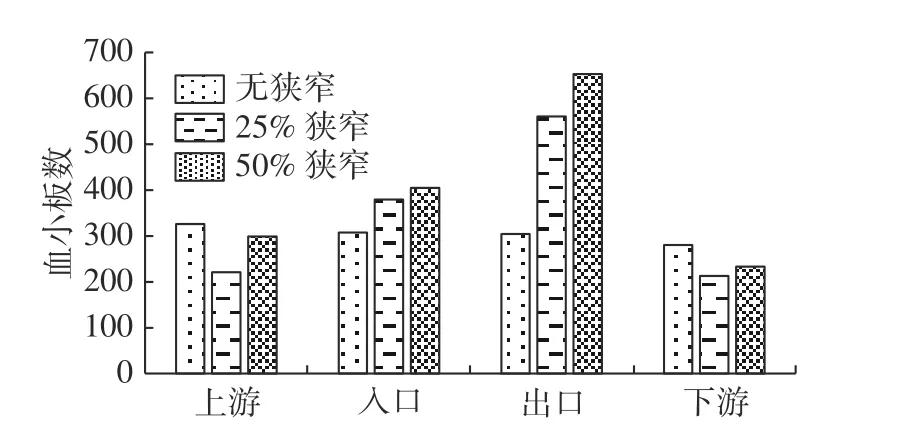
图7 0.5 s 时不同狭窄程度下血栓在不同破损区域的生长情况

3.2 仿真实验效率比较与分析

在仿真使用模型的血栓模块中，结合了窄带法的自适应细化网格被使用在水平集方程求解上，以降低需要存储和计算的数据量。图8 是在网格间距为血小板半径和2.5 倍血小板半径下进行仿真实验的血栓形态。按血栓模块设计的DRLSE 方法，血栓能够较为完整地保留血小板的球状形态。使用粗网格的实验中，由于水平集演化方程求解中的误差，血栓中血小板形态出现失真和变形；在网格细化提高计算精确度后，血小板的形态得到了更好地保留。

图8 不同网格间距下血栓的形态

在水平集方法中，窄带法虽然可以降低算法的计算量，但均匀的局部细化仍然会导致数据的冗余。图9 是无狭窄、狭窄度为25% 和50%这3 种情况下，局部均匀细化和非均匀的自适应细化下网格数量随血栓生长的曲线图。虽然在血栓生长至一定程度后细化网格增长不再明显。但随狭窄程度增加，均匀细化下网格数量成倍增长。使用自适应局部细化后，网格数量下降至均匀细化的2%，并且狭窄程度和血栓生长对细化网格数量无明显影响。

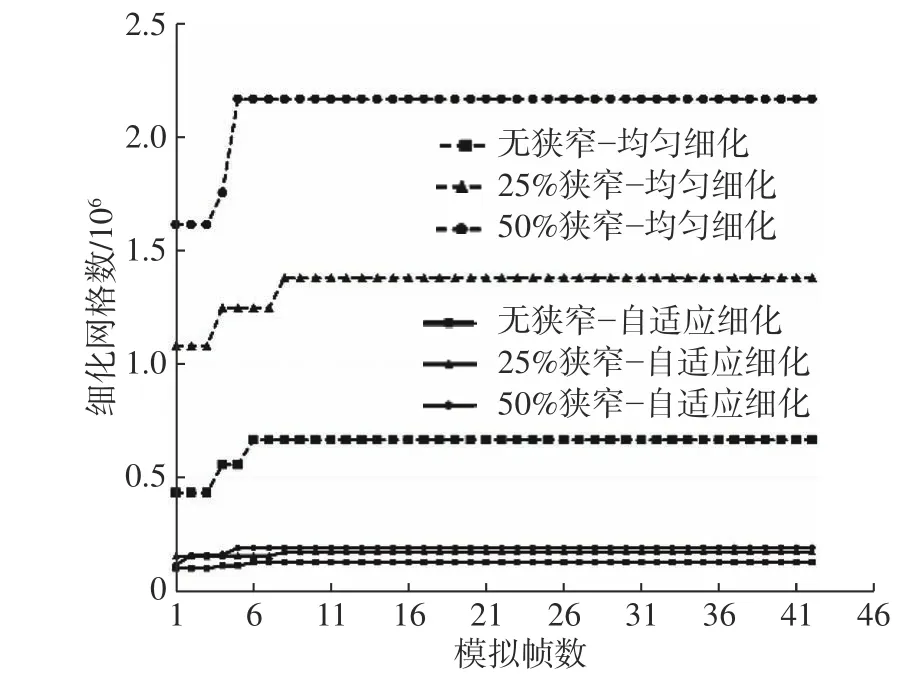
图9 仿真过程中不同狭窄程度下细化网格数变化曲线

4 结论

本研究中针对初期血栓形成机制的研究，建立了基于水平集的计算模型，并采用自适应的局部细化网格和DRLSE 方法优化了水平集函数求解过程。通过研究，得出结论如下：

1)本文提出的初期血栓形成计算模型能够被用于实现狭窄血管中初期血栓形成的仿真实验，实验结果展示的狭窄对血栓形成的影响情况与动物实验一致。

2)通过实验分析可知，血管狭窄会促进血栓的形成，血小板在狭窄出口处的聚集较为明显，血管堵塞的风险较大。

3)结合了局部水平集和笛卡尔自适应网格的自适应局部细化网格可以在提高计算精确度的基础上有效降低模型计算中水平集函数求解的数据量。

4)文中所提出的计算模型虽然引入了vWF在血栓形成中的作用，但仍有更多的凝血因子可以加入模型以提高模拟过程的完整性，这也是下一步研究工作的重点内容。