基于迭代重构算法改进晶体衍射分光X 射线鬼成像的图像质量研究*

张海鹏 赵昌哲 鞠晓璐 汤杰 肖体乔‡

1) (中国科学院上海应用物理研究所,上海 201800)

2) (中国科学院大学,北京 100049)

3) (中国科学院上海同步辐射光源/上海高等研究院张江实验室,上海 201204)

X 射线鬼成像是一种低剂量、非定域成像方法,对医疗诊断和生物成像具有重要意义.在基于晶体劳厄衍射分光的X 射线鬼成像中,晶体振动会造成衍射光路上散斑的模糊,进而导致利用关联方法重构图像衬度和空间分辨的降低.本文系统分析了衍射光路上散斑图像的模糊程度对归一化二阶关联函数g(2) 的最大值和半高全宽的影响.模糊程度的增强会导致 g(2) 最大值的减小和半高全宽的展宽,在理论上证明了模糊程度会引起重构图像的衬度和分辨能力的降低.为解决上述问题,本文在衍射光路和直通光路的直接关联方法(GLH)的基础上提出 GLHE方法(GLHenhanced method).模拟实验表明 GLHE 算法能同时改善图像衬度和提高重构分辨率,并且模糊程度增强时,GLHE 算法重构图像的峰值信噪比与先对直通光路的散斑图像进行高斯滤波处理再进行双光路关联计算方法(GLL)的差距扩大,同时保证其对噪声的鲁棒性.本文为晶体衍射分光的X 射线鬼成像的实际应用提供可行的思路.

1 引言

鬼成像(ghost imaging,GI),又名关联成像,是一种对光场强度涨落进行关联运算的非定域成像方法[1-7].1985 年,美国马里兰大学的史砚华组基于自发参量下转化产生的纠缠光子对在实验上首次实现鬼成像和鬼干涉[4,8].起初,量子纠缠被认为是鬼成像的先决条件,但之后Bennink 等[9]利用经典热光成功完成鬼成像实验,否认了鬼成像是纠缠光特有的性质.经过30 多年的发展,经典热光鬼成像作为全新的非定域成像技术正逐步从理论研究走向实际应用.鬼成像独特的优越性体现在其灵活的双光路设计上.根据实际需求配置光路,“鬼”图像可以在弱光照[10]或扰动环境中[11-13]获得超越瑞利衍射极限的空间分辨[14],因此鬼成像在远程遥感[15,16],量子光刻[17,18],保密通讯[19]等诸多领域受到广泛关注.

2004 年,程静等[20]在理论上给出利用经典热光进行无透镜鬼成像的实验方案,而后吴令安等[21,22]在实验上证实了无透镜鬼成像方案的可行性.无透镜鬼成像方案表明鬼成像技术可从可见光延伸到任意波段,包括电子[23]、中子[24]和X 射线[25-32]等.利用X 射线短波长、深穿透的特性,X 射线鬼成像(X-ray ghost imaging,XGI)常被用于探测物体内部的精细结构,尤其是在医疗诊断、晶体分析和生物成像等诸多科学与技术领域中.目前理论与实验均已证明X 射线鬼成像采用参量下转换产生的纠缠X 光[30],掩模调制强度波动的赝热X 光[27,29,32],甚至单束团产生的真热X 光[31]等不同X 光源都能准确重构目标图像.2016 年,根据傅里叶变换鬼成像理论,俞虹等[32]利用多孔金属箔调制的随机涨落的赝热X 光同时恢复出多缝样品的振幅和位相,并且其成像分辨率甚至超越具有空间分辨能力的探测器的像素尺寸.

然而,由于X 光中没有合适可靠的光学元件能分出两束相同强度分布的散斑花样,因此通常将待测物体移进和移出光路以分别模仿X 射线鬼成像中的信号光路和参考光路[27,32].但物体移进移出光路会导致采样效率低下,单次采样耗时过长,不适合实际应用场景.此外,计算X 射线鬼成像[28,33]方法,通过特殊设计的掩模推算在物体平面处光场的强度分布,可以避免分光引入的困扰,同时能调节光强涨落分布模式以优化图像重构质量,但是掩模的设计与制作却受限于微纳加工工艺.因此,在X 射线鬼成像的实际应用中经常采用晶体作为分束器,利用衍射效应复制出两幅相同强度分布的光场[25,26,29,31].2016 年,Pelliccia 等[31]在ESRF 用薄晶衍射的方法获得两幅由单束团产生的相同分布的随机热光场,并成功重构出铜丝的吸收衬度图像.2018 年,该研究组[25]用硅单晶对粉光分束且重构出真实复杂样品-钨灯丝图像.同年,Kingston等[26]利用晶体衍射分光鬼成像重构出铝泡沫物体的断层扫描图像(ghost tomography).然而由于晶体振动的缘故,相比直通光路散斑图像,衍射光路的散斑图像细节模糊,光强涨落起伏微弱.本文系统分析了在X 射线鬼成像中衍射光路上散斑图像的模糊程度对重构图像质量的影响,并提出改进方案,以期改善重构图像的衬度,提高成像的空间分辨率.

2 理论分析

图1 是基于晶体衍射分光的X 射线鬼成像的光路示意图.单色X 光通过掩模(mask)后产生强度涨落的散斑花样,经过晶体(crystal)衍射分光后在直通光路(transmitted beam)产生高清的散斑图样,再被具有空间分辨的探测器(spatially resolved detector)记录;在衍射光路(diffracted beam)上,由晶体振动引起的模糊散斑图像(x,y)经过待测物体T(x,y) 后由桶探测器(bucket detector)收集为单值信号.

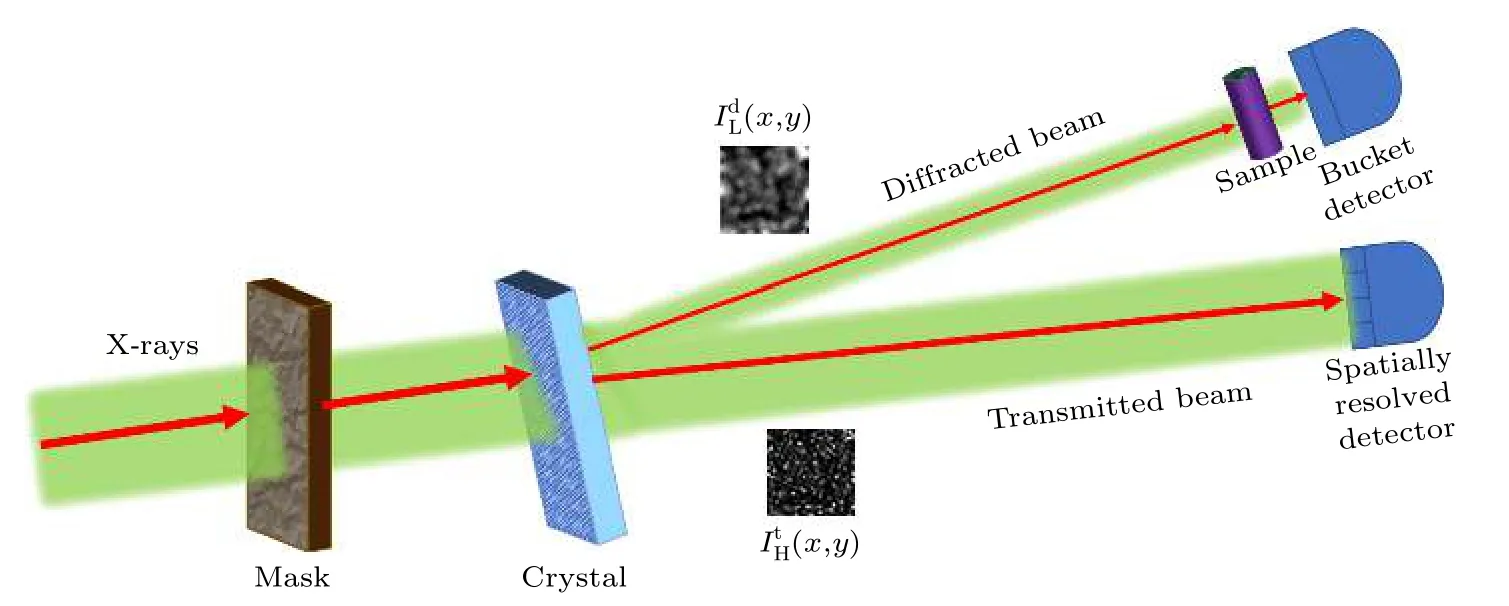
图1 基于晶体衍射分光的X 射线鬼成像示意图Fig.1.Schematic diagram of X-ray ghost imaging based on the beam splitter of crystal diffraction.

根据传统鬼成像算法[29],即直接关联计算衍射光路上的信号和直通光路上的散斑图样,重构如下式所示:

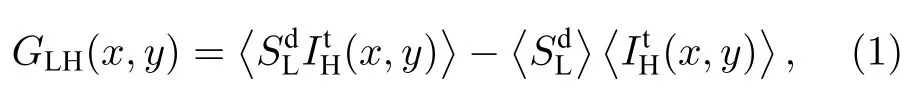
实验中Kingston 等[26]将高斯滤波转变为与的强度分布几乎一致,即

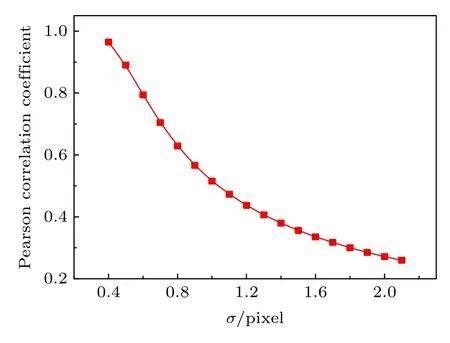
图2 一致性和模糊程度关系Fig.2.Consistency vs ambiguity.

Kingston 等[26]将直通光路上的散斑图像模糊后,再与衍射光路的桶信号关联计算,以提高恢复图像的质量,如下式:

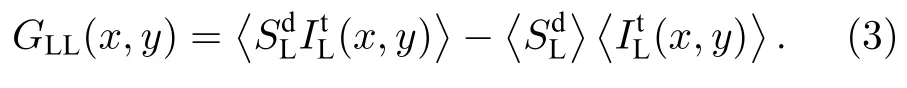
但是散斑图像的模糊不仅会使光强不再服从负指数分布,减弱强度涨落程度,而且会导致不规则散斑的平均尺寸增大,即改变两光路上强度的归一化二阶关联函数从而影响图像重构质量,其中去除平均背景后的表达如下[35],

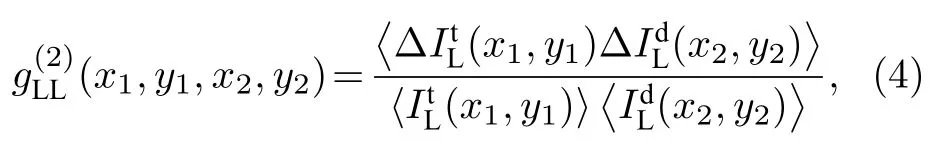
理论上,若衍射光路中的散斑图像与直通光路中为相同的高清图像时,重构图像衬度与分辨率都是最佳的,其去平均背景后强度的归一化二阶关联函数表达如下,

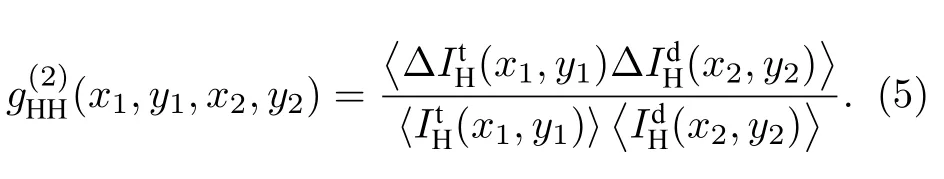
若高清散斑图像中不规则散斑的平均尺寸远小于1 个像素(下文中高清图像都表示散斑尺寸小于1 个像素),则

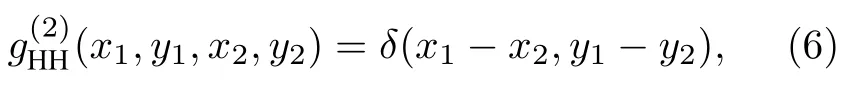
其中δ(x1-x2,y1-y2)是狄拉克函数.最大值为1,且半高全宽小于1 个像素,则能达到具有分辨的探测器所能达到的最佳分辨.但在晶体衍射分光的X 射线鬼成像中,衍射光路的散斑模糊会改变直接关联GLH对应的归一化强度关联函数即

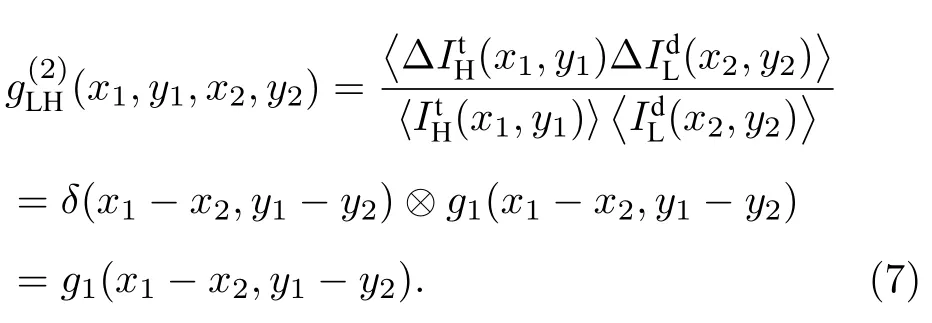
若如Kingston 等[26]提出的,先将直通光路的散斑图像滤波处理后,再用(3)式重构图像,其对应的产生变化,即

当衍射光路中的散斑图像相对直通光路中的模糊程度所对应的标准差σ为 1.3 个像素时,根据上述理论可得,和的最大值分别为0.0471和0.0942,其半高宽分别为4.320和3.055 个像素.此外,我们模拟出直通光路上的高清散斑图像,并通过高斯函数g1将其模糊后作为衍射光路上的散斑图像,利用(7)式计算出两光路间光强的归一化二阶关联分布,并用高斯函数进行拟合,则的最大值为0.0942,而半高全宽为3.032.若如Kingston 等[26]的处理方案,先将直通光路散斑图像滤波后再与衍射光路上的散斑图像进行二阶关联计算,则的最大值为0.0468,而半高宽为4.343.由此发现模拟散斑后再通过二阶关联计算的结果和理论结果几乎一致.如图3 所示,比较模拟散斑计算的分别和理论上所对应的g2,g1在x方向的分布,结果表明模拟和理论的曲线几乎完全吻合.

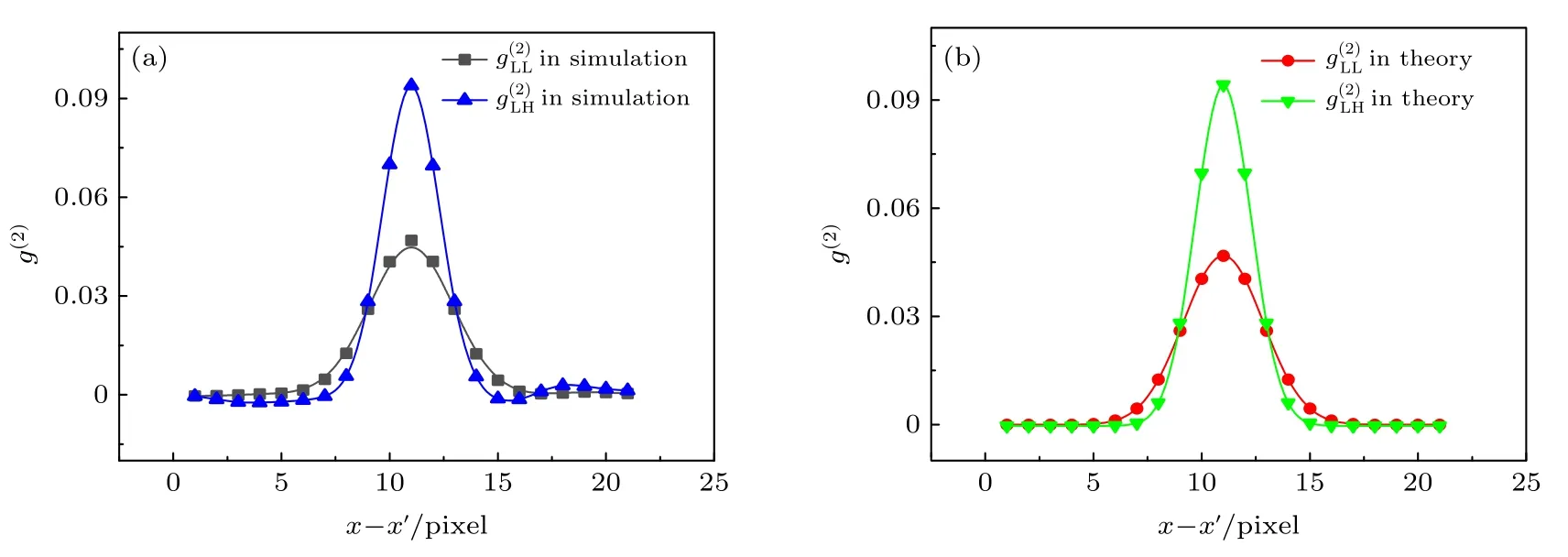
图3 当 σ=1.3时光强归一化二阶关联的理论和模拟在x 方向上的曲线图 (a) 和的模拟在x 方向上的曲线图;(b)和的理论在x 方向上的曲线图Fig.3.The theoretical and simulated curves of the normalized second-order correlation of light in tensityinxdirection when σ=1.3:(a) The simulated curves ofand inx direction;(b) the theoretical curves ofand inxdirection.

随着模糊程度的增大,即标准差σ增大,理论上的最大值都在减小,而半高全宽都在增大.如图4 所示,在理论和模拟上随标准差σ的变化趋势.理论和模拟上的结果高度一致,同时也可预测随着模糊程度的增加,两种方案重构图像质量也在逐步恶化.

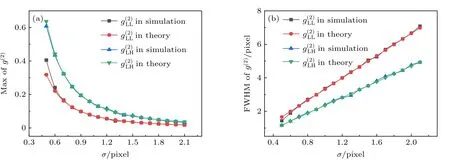
图4 和在理论和模拟上随模糊程度 σ 的变化曲线图 (a) 和在理论和模拟的最大值随 σ 的变化;(b) 和在理论和模拟的半高全宽随 σ 的变化Fig.4.and vary with the blur degree σ in theory and simulation:(a) The theoretical and simulated maximum of andvary with σ;(b) the FWHM of and vary with σ in theory and simulation.

3 解决方案

为了改善Kingston 等[26]提出的方案中,因最大值的减小和半高全宽的增大而引起的GLL重构图像衬度低且细节模糊的后果,在GLH的基础上提出一种GLH增强算法(GLHenhanced method,GLHE),目标是希望图像衬度和分辨率能达到GHH的效果,其中GHH是在两光路上为相同的高清散斑图像时通过关联计算重构图像的方案.GHH表达如下:

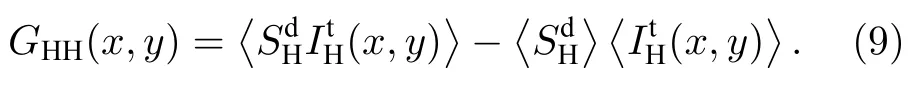
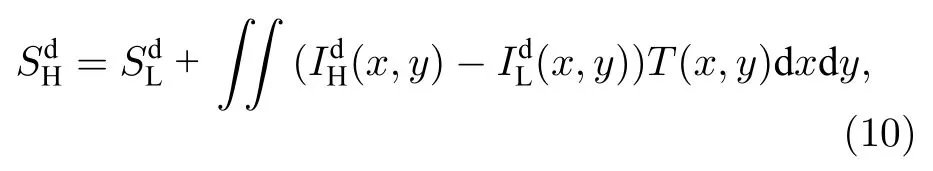
选择图5(a)作为待测物体,其图像大小为32×32像素,线宽为3 个像素,采样数量为50000张.如图5 所示是GLL方法和GLHE 方法在不同模糊程度时重构图像比较.随着标准差σ的逐渐增大,理论上GLL重构图像的衬度和空间分辨会逐步变差.从图5(b)到图5(f)重构的图像在直观上也是衬度在逐步减弱,细节愈加模糊,这与理论一致,尤其在图5(c)中(σ1时GLL重构的图像),此时对应的半高全宽为3.32 个像素,超过待测物体的线宽.相比图5(b),图5(c)的条纹边缘明显更加弥散,几乎不能准确衡量待测物体的线宽.模拟中模糊程度对应的标准差相邻间隔为0.3,在理论上分辨率相差 0.3×3.32≈1 个像素,则相邻的GLL重构的图像在衬度和分辨率上有明显的差异以供区分.

图5 GLL和 GLHE方法重构图像 (a) 物体图像;(b)—(f) 不同标准差(σ=0.7,1.0,1.3,1.6,1.9)时 GLL恢复的图像;(g)GHH重构的图像;(h)—(l) 不同标准差(σ=0.7,1.0,1.3,1.6,1.9)时 GLHE 方法恢复的图像.Fig.5.Images reconstructed by GLLand iterative method:(a) The object image;(b)-(f) the images are retrieved by GLLwithσ set as 0.7,1.0,1.3,1.6,1.9;(g) the image restored by GHH;(h)-(l) the images are reconstructed by iterative method when σ is 0.7,1.0,1.3,1.6,1.9.

图5(g)是GHH重构的高衬度、高分辨的图像,其能够完全分辨目标图像的线宽.图5(h)到图5(l)是GLHE 方法迭代3次时重构的图像,在视觉效果上衬度几乎未发生明显变化,且随着σ的增大,GLHE方法重构图像的线宽略微增加.纵向比较,当σ相同时,GLHE方法重构图像比GLL的衬度明显提高,在 GLL几乎不能区分图像线条时,GLH依然有足够能力区分图像线形,即GLHE方法相比GLL在分辨能力上有明显提升.此外,如图6 所示,随着σ的增大,两种方法恢复图像的PSNR 都逐渐下降,但两者PSNR 的间距也在扩大,表明GLHE 方法重构图像质量的提升愈加明显.

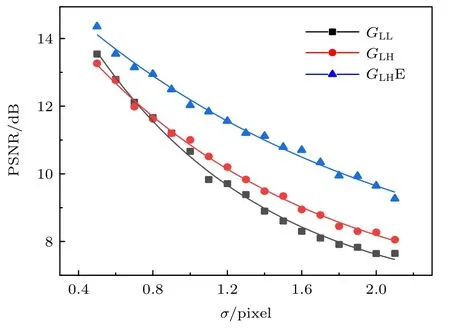
图6 不同算法重构图像的PSNR 随模糊衬度的变化曲线Fig.6.The PSNR curves of reconstructed images with different algorithms vary with blur degree.

选取图5 重构图像中间宽度为3 像素的区域绘制轮廓线,其平均结果如图7 所示.图7(a)是图5上行图像的轮廓线.随着标准差σ的增大,图7(a)中曲线的峰(如②峰)与谷(如①谷)间距减小,则图像的衬度逐渐减小.峰与谷之间曲线的倾斜逐渐平缓(如①谷与②峰之间曲线的陡峭程度在减弱),则重构图像的分辨能力下降.上述都与图5 中GLL重构图像的直观效果一致.图7(b)是图5 下行图像的轮廓线.图7(b)中的曲线几乎都重叠在一起,表明不同标准差σ时,GLHE算法重构图像的轮廓曲线的峰(如④峰)与谷(如③谷)的间距与GHH的非常接近,同时峰谷之间曲线的倾斜也几乎相同,表明GLHE 重构图像的衬度和分辨率几乎都与GHH的相同,这与GLHE 的目标是一致的.比较图7(a)和图7(b)发现,在相同σ时,图7(b)中曲线的陡峭程度明显比图7(a)中对应曲线的大,表明GLHE比GLL的空间分辨能力强,且随着σ的增大,图7(b)中峰谷间距比图7(a)中应曲线的大出很多,表明GLHE重构图像的衬度也比GLL都有明显提高.总结而言,GLHE比GLL在衬度,分辨率和PSNR 上都有明显改改善,尤其是在σ1.3 时,GLHE 重构图像的PSNR 比GLL提高约2 dB,分辨率也从4.32 个像素提高到小于3 个像素(能清晰分辨待测物体3 个像素的线宽),衬度(可见度其中〈Gobj〉表示重构物体即白色区域的平均灰度值,而〈Gbg〉表示背景图像即黑色区域的平均灰度值)提高约1 倍.

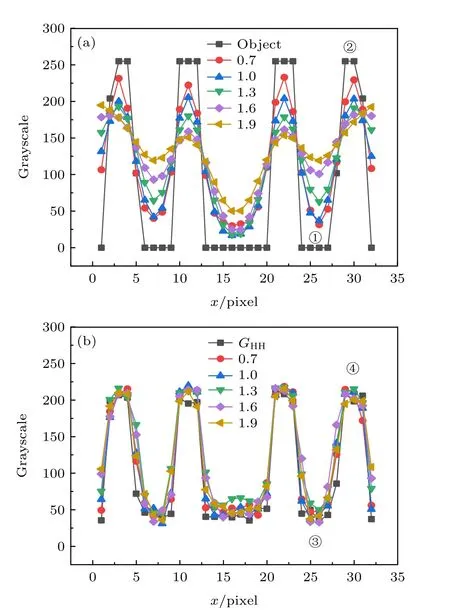
图7 GLL和 GLHE 方法重构图像中间部位的截面轮廓线：(a) 黑线是物体的截面轮廓线,即图5(a)中间区域的平均灰度变化,其余分别是 GLL方法在 σ 为0.7,1.0,1.3,1.6,1.9 时重构图像的截面轮廓线,即图5(b)到图5(f)的中间区域的平均灰度变化;(b) 黑线是GHH 重构图像的截面轮廓线,即图5(g)中间区域的平均灰度变化,其余是 GLHE 方法在 σ 为0.7,1.0,1.3,1.6,1.9 时重构图像的截面轮廓线，即图5(h)到图5(l)的中间区域的平均灰度变化.Fig.7.Line profiles of the middle parts in the reconstructed images by GLLand GLHE :(a) The black curve is the line profile of the object,that is the mean grayscale change of the middle part in Fig.5(a),and the rest is the line profiles of the images retrieved by GLLwith σ set as 0.7,1.0,1.3,1.6,1.9,that is,the mean grayscale change of the middle part in Fig.5(b) to Fig.5(f);(b) the black curve is the line profile of the image retrieved by GHH,that is the mean grayscale change of the middle part in Fig.5(g),and the rest is the line profiles of the images restored byGLHE when σ is 0.7,1.0,1.3,1.6,1.9,that is,the mean grayscale change of the middle part in Fig.5(h) to Fig.5(l).

考虑到在实际实验过程中存在噪声,并且其主要来源于探测器引入的加性高斯白噪声,因此在理论上首先证明加性高斯白噪声对基于系综平均的重构算法是无影响的.设参考光路的光斑强度分布为∑I(x1,y1),在信号光路中桶探测器的信号为其中 (xk,yk) (k=1,2)表示在探测器平面的位置.在无噪声时,重构结果如下:

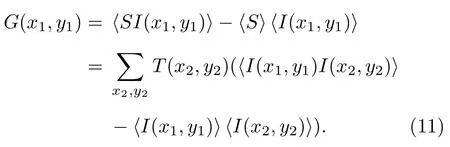
当探测器引入加性噪声时,则参考光路的光强分布In(x1,y1)I(x1,y1)+N1(x1,y1),在信号光路中桶探测器的信号为N2(x2,y2),下标n表示含噪,Nk(k=1,2)表示均值为μN,标准差为σN的同类噪声,则在有噪声重构如下:

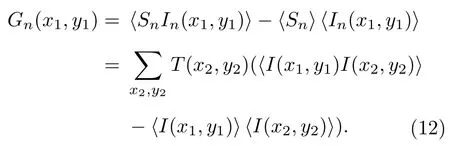
从推导看G(x1,y1) 与Gn(x1,y1) 在充足采样时结果是相同的.

下面用模拟实验证明基于系综平均的GLL,GLHE和GHH重构图像对于噪声是不敏感的.添加均值μN为0.1,标准差σN=0.05,0.1,0.15,0.2,0.25 的不同高斯噪声,对于服从负指数分布且均值为1 的散斑图样而言,相应的信噪比分别为44.0 dB,40.0 dB,35.8 dB,32.0 dB,28.8 dB,则GHH,GLL和GLHE 在模糊程度对应的标准差为1.3 时重构图像如图8 所示.直观上在不同噪声时,GHH,GLL,GLHE 各自重构图像在分辨率和衬度上区别很小,表明基于系综平均的GHH,GLL,GLHE 方法对于噪声有较强的鲁棒性.不同噪声时,GHH,GLL,GLHE方法重构图像的PSNR 亦是几乎不变的,如图9所示,这同样表明GHH,GLL,GLHE 方法重构质量几乎不受噪声影响.数值模拟的结论与理论推导是一致的.

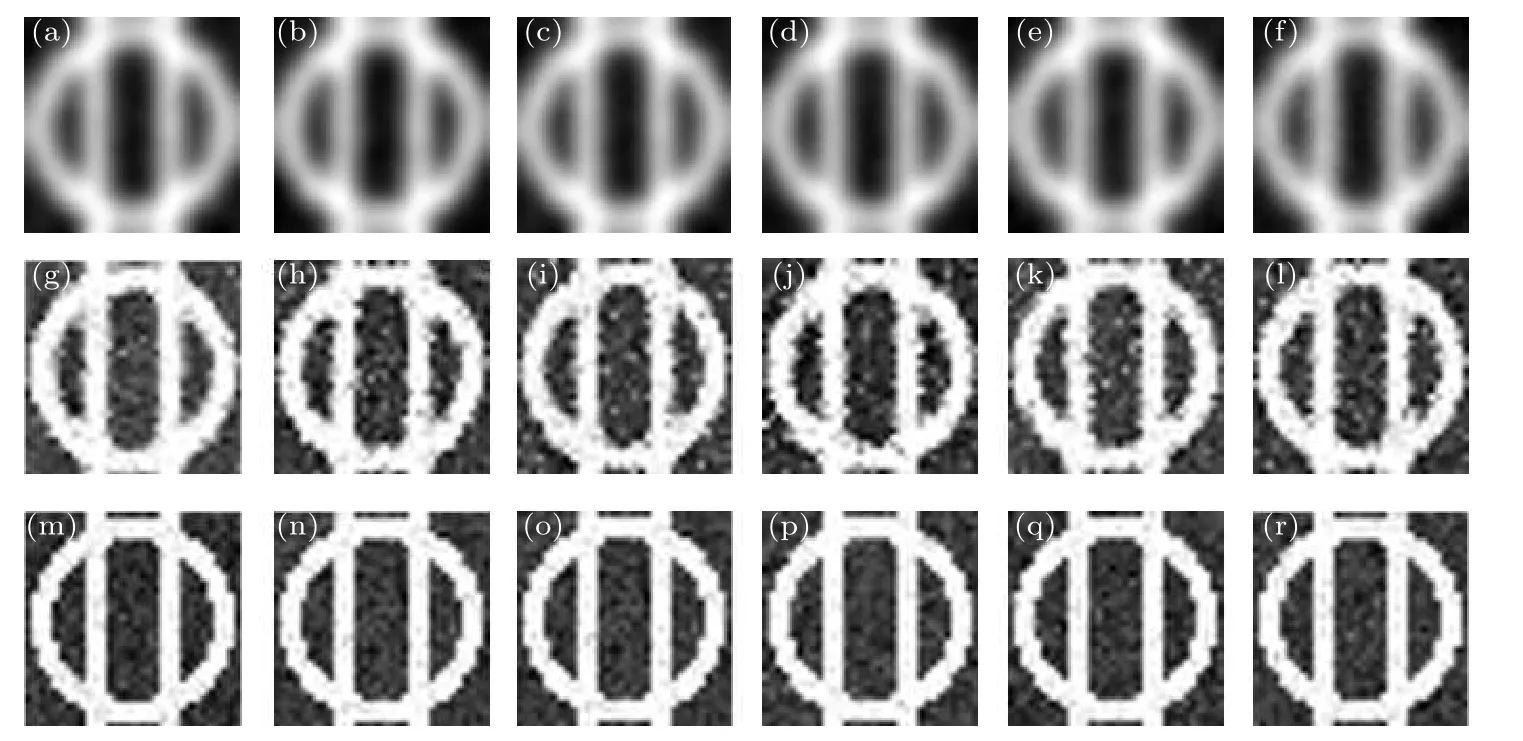
图8 GLL,GLHE,GHH在不同噪声下重构图像:(a),(g),(m) 无噪声时 GLL,GLHE,GHH重构的图像;(b)—(f) GLL 在均值为0.1,标准差为0.05,0.1,0.15,0.2,0.25 时重构的图像;(i)—(l) GLHE 在均值为0.1,标准差为0.05,0.1,0.15,0.2,0.25 时重构的图像;(n)—(r) GHH 在均值为0.1,标准差为0.05,0.1,0.15,0.2,0.25 时重构的图像Fig.8.Images reconstructed by GLL,GLHE,GHHunder different noise:(a),(g),(m) the images reconstructed by GLL,GLHE,GHHwithout noise;(b)—(f) the images reconstructed by GLL under the noise with the mean of 0.1 and the standard deviation of 0.05,0.1,0.15,0.2,0.25 respectively;(i)—(l) the images reconstructed by GLHE under the noise with the mean of 0.1 and the standard deviation of 0.05,0.1,0.15,0.2,0.25 respectively;(n)—(r) the images reconstructed by GHH under the noise with the mean of 0.1 and the standard deviation of 0.05,0.1,0.15,0.2,0.25 respectively.

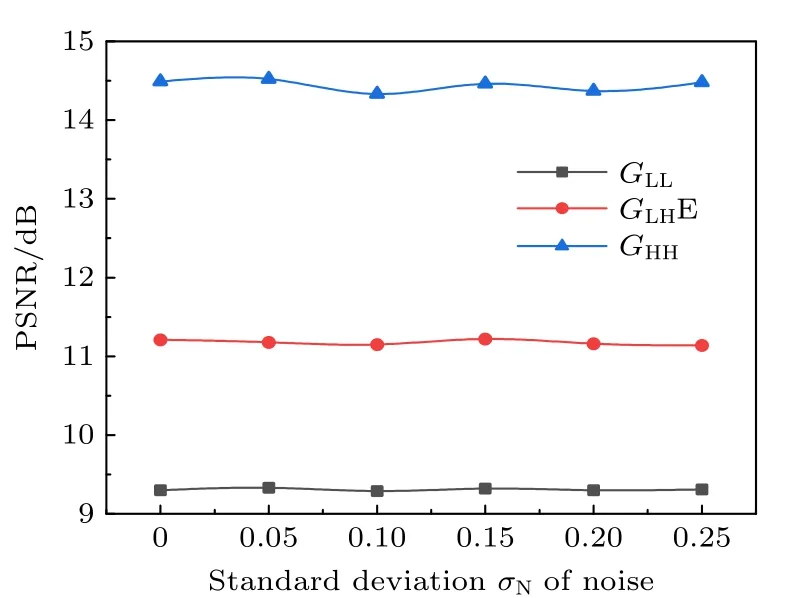
图9 GLL,GLHE,GHH 在不同噪声下重构图像的PSNR,其中标准差 σN为0表示没有噪声(此时噪声均值 μN 也为0)Fig.9.PSNRs of images reconstructed by GLL,GLHE,GHHunder different noise,where the standard deviation σNof 0 indicates there is no noise (at this time the mean μNof noise is also 0).

4 结论

在基于晶体衍射分光的X 射线鬼成像中,衍射光路中散斑图像的模糊会造成重构图像质量下降.若直接将直通光路的高清散斑图像与衍射光路的数值信号进行关联计算(即GLH方法),由于两光路散斑花样的不一致性,即Pearson 相关系数会随着模糊程度的增强而下降,重构图像的质量会逐步恶化.为了解决这一问题,Kingston 等[26]提出将直通光路的散斑图像滤波模糊处理,以保证衍射光与直通光路上散斑图像的一致性,然后再将两光路上的图像进行关联计算(即GLL方法).但这种方法会削弱光强涨落的起伏程度,减小归一化关联函数g(2)的最大值,降低图像衬度,同时会增大散斑的平均尺寸,增大g(2)的半高全宽,导致空间分辨变差.

本文系统地研究了在晶体衍射分光的X 射线鬼成像中,由于晶体振动导致的衍射光路上散斑的模糊程度对于成像衬度和空间分辨的影响.本文首先分析了散斑的模糊程度对强度的归一化二阶关联函数g(2)的影响,并发现随着模糊程度的增强,g(2)的最大值在减小,半高全宽在增大,从理论上证实了衍射光路的模糊散斑对关联算法重构质量的影响.为解决上述问题,本文在衍射光路和直通光路上信号直接关联GLH的基础上提出GLHE 方法.模拟实验表明GLHE 方法能够同时改善重构图像的衬度和分辨率,并且衬度和分辨率几乎不随模糊程度而改变.此外,随着模糊程度的增强,GLHE 方法重构图像的峰值信噪比与GLL方法的差距扩大,且对噪声有较强的鲁棒性.本文发展的方法显著改善了晶体衍射分光鬼成像的衬度和分辨率,为该方法的进一步推广应用解决了一个关键技术,在生物医学、材料科学的高效、高分辨X 射线鬼成像研究中具有重要应用前景.课题组正在致力于在上海光源建立晶体分光鬼成像方法,并开展相关应用研究[36].

感谢上海光源束线工程部李中亮研究员和司尚禹博士的讨论与建议.