Belief Combination of Classifiers for Incomplete Data

Zuowei Zhang,, Songtao Ye, Yiru Zhang, Weiping Ding,, and Hao Wang,

Abstract—Data with missing values, or incomplete information,brings some challenges to the development of classification, as the incompleteness may significantly affect the performance of classifiers. In this paper, we handle missing values in both training and test sets with uncertainty and imprecision reasoning by proposing a new belief combination of classifier (BCC) method based on the evidence theory. The proposed BCC method aims to improve the classification performance of incomplete data by characterizing the uncertainty and imprecision brought by incompleteness. In BCC, different attributes are regarded as independent sources, and the collection of each attribute is considered as a subset. Then, multiple classifiers are trained with each subset independently and allow each observed attribute to provide a sub-classification result for the query pattern. Finally,these sub-classification results with different weights (discounting factors) are used to provide supplementary information to jointly determine the final classes of query patterns. The weights consist of two aspects: global and local. The global weight calculated by an optimization function is employed to represent the reliability of each classifier, and the local weight obtained by mining attribute distribution characteristics is used to quantify the importance of observed attributes to the pattern classification. Abundant comparative experiments including seven methods on twelve datasets are executed, demonstrating the out-performance of BCC over all baseline methods in terms of accuracy, precision,recall, F1 measure, with pertinent computational costs.

I. INTRODUCTION

CLASSIFICATION is a traditional and prevalent problem in data analysis, aiming to identify objects to the categories they belong to. Incompleteness problem in data is one of critical challenges in classification applications, caused by various data collection or access mechanisms. Incomplete data, also called incomplete patterns or missing data, refers to the data with missing values, attributes, or contents1To avoid ambiguity, we apply the term incomplete data for a dataset with missing values, and incomplete pattern for a pattern with missing values.. This phenomenon has affected classification applications with unsatisfactory results [1]–[3]. The incompleteness of data is a critical issue in risk-sensitive fields, such as industrial systems[4], [5], health management [6] and financial market [7].Many methods have emerged to resolve the incompleteness issues around three types of missing mechanism [4], [8]–[10]:such as missing completely at random, missing at random, not missing at random. These methods can be roughly categorized into four groups:

1) Deletion methods. The pattern with missing values is simply discarded. The deletion method is only applicable to cases where the number of incomplete patterns accounts for a small proportion (less than 5%) of the whole dataset [8], [11].It inevitably leads to a waste of patterns that are difficult (or costly) to obtain sometimes.

2) Model-based methods. The missing values are imputed based on statistical assumptions of joint distribution, then the fulfilled patterns are classified by conventional classifiers. For example, a (supervised) logistic regression algorithm is proposed in [12] to deal with incomplete datasets, where the missing values are modeled by performing analytic integration with an estimated conditional density function (conditioned on the observed data) based on the Gaussian mixture model(GMM) [13]. However, the approximated model is not robust enough, bringing over-fitting or under-fitting problems.

3) Machine learning methods. Incomplete patterns are directly used to train some specific classifiers. For decision trees, in algorithm C4.5 [14], missing values are simply ignored in gain and entropy calculations, while C5.0 [15] and CART neural network [16] employ imputative frameworks[17]. In Hybrid neural networks [18], missing values are imputed by two FCM (fuzzyc-meams) based methods. In a support vector solution [19], the modified support vector machine generalizes the approach of mean imputation in the linear case by taking into account the uncertainty of the predicted outputs. In word embedding models [20], the missing attributes are usually valued as 0, which can be regarded as imputation. When most of the attributes are lost,however, the classification performance of these methods is often unsatisfactory.

4) Estimation methods. This is the most widely used methods for dealing with incomplete data. The missing value is replaced (imputed) with an estimation [3], and then the pattern with estimations is classified by conventional classifiers (e.g., Bayes classifier [21]). We will review some estimation-based methods separately.

There are some popular and representative methods for estimating missing values. The simplest method is the mean imputation [22], where the missing values are imputed by the mean of the observed values of the corresponding attribute.Knearest neighbor imputation (KNNI) [23] is another simple idea, in which various weights depending on the distances between the neighbors and the incomplete pattern are designed to model the different effects of neighbors on the missing values. In [24], fuzzyc-means imputation (FCMI),the missing values are imputed according to the clustering centers generated by FCM and the distances between one object and all the centers. There are also other effective methods for dealing with incomplete data, such as the selforganizing maps (SOM) imputation [9], and the regression imputation [8], [12]. In particular, a fuzzy-based information decomposition (FID) method [25] was proposed recently to address the class imbalance and missing values problem simultaneously. In FID, the incomplete pattern is imputed and used to create synthetic patterns for the minority class to rebalance the training data. In [26], it is assumed that two batches extracted randomly in the same dataset have the same distribution. Then optimal transport distances are leveraged to quantify that criterion and turn it into a loss function to impute missing data values. Besides, practical methods are proposed to minimize these losses using end-to-end learning that can exploit parametric assumptions on the underlying distributions of values. Moreover, some works [27]–[31] are devoted to multiple imputations for missing values to model the uncertainty of the incomplete pattern caused by the lack of information. For example, in [29], a novel method, based on the generative adversarial network (GAN) framework [32],attempts to model the data distribution and then performs multiple imputations by drawing numerous times to capture the uncertainty of the interpolated values. These estimationbased methods assume reasonable correlations between missing and observed values, which are not always reliable.

In addition to the issues mentioned above in each type, most methods, such as deletion, model-based, and estimation methods, treat only missing values and do not consider the negative impact of missing values on the classification.Although machine learning-based methods can classify missing values, they do not consider the uncertainty caused by missing values in the process, therefore their performances are sometimes not robust. Targeting on these limitations, the motivation of our work is based on the following three aspects.

1) Comparing to the deletion method, we investigate a method that does not remove any observed information since this information may be precious.

2) Comparing to model-based and estimation methods, we develop a method that does not introduce new uncertainties since statistical assumption will cause uncertainty.

3) Comparing to machine learning methods, we aim to improve the classification performance by modeling missing values with uncertainty and imprecision considered.

Based on the above analysis, we observe that these methods focus on the test set and assume that the training set is complete in most cases. When the training set is incomplete,the incomplete patterns are either imputed for completion or deleted directly. Moreover, these methods tend to directly model missing values, such as estimation strategies or model prediction. However, this would bring new uncertainties because estimated values can never replace the real world. In this case, this paper aims to answer an important question:how to improve the classification accuracy of incomplete data without losing information or introducing new uncertainty information in the presence of many missing values in both training and test sets? To drive such an answer, we design a new belief combination of classifiers (BCC) method for missing data based on evidence theory.

Evidence theory [33], [34] has been widely used in pattern classification since it is an efficient tool to characterize and combine uncertain and imprecise information, and it can well compromise (more or less) useful supplementary information provided by different sources in classifier fusion [35]–[37].For instance, a classifier combination method depending on the concepts of internal reliability and relative reliability is proposed for classifier fusion with contextual reliability evaluation (CF-CRE) [38] based on evidence theory, where the internal reliability and relative reliability capture different aspects of the classification reliability. For non-independence classifiers, the literature [35] studies a method of combining other operators (i.e., parameterizedt-norm) with the Dempster’s rule, aiming to make their behavior between the Dempster’s rule and the cautious rule. In [36], the transferable belief model (TBM) [39], an uncertain reasoning framework based on evidence theory, is employed to improve the performances of mailing address recognition systems by combining the outputs from several postal address readers(PARs). Reputably, the idea of group decision-making is introduced in [40] for reasoning with multiple pieces of evidence to identify and discount unreliable evidence automatically. The core is to construct an adaptive robust combination rule that incorporates the information contained in the consistent focal elements. These classifier fusion methods based on evidence theory have achieved satisfactory performances. However, they are designed for complete patterns. The uncertainty brought by the incompleteness can also be considered in the data process [6], [41], making one of the key ideas of this paper.

The proposed method, named belief combination of classifiers (BCC), is able to characterize the uncertainty and imprecision caused by missing values both in training and test sets without imposing assumptive models. The main contributions of this paper cover the following aspects:

1) A novel classification method based on evidence theory is proposed, applicable for data with missing values, where incompleteness may exist in both training and query sets. To overcome the incompleteness in patterns, classifiers are trained by subsets of attributes, leading to sub-classification results.

2) Uncertainty and imprecision reasoning is used for missing values, used for training multiple classifiers.Afterwards, multiple evidential sub-classification results are combined for a final decision. Such designs with the context of uncertainty and imprecision make the classification results more robust.

3) An optimization function is designed to calculate the global weight to represent the reliability of each classifier, as well as the local weight obtained by mining attribute distribution characteristics is used to quantify the importance of observed attributes to the pattern classification. Moreover,abundant experiments are conducted, demonstrating the supremacy of BCC over many conventional methods in terms of classification results.

The remainder of this paper is organized as follows. After a brief introduction of evidence theory in Section II, the belief combination of classifiers (BCC) method for missing data is proposed in detail in Section III. Simulations results are presented in Section IV to evaluate the performance of BCC with different real datasets. Finally, Section V concludes the entire work and gives research perspectives.

II. BASICS OF EVIDENCE THEORY

Evidence theory, also known as Dempster-Shafer theory(DST) or the theory of belief functions, is firstly introduced by Dempster [33], then developed by Shafer in hisA Mathematical Theory of Evidence[34]. Evidence theory is considered as an extended version of fuzzy set theory and has been widely used in data fusion [36], [39], [40], decisionmaking [37], [42], [43], clustering [44]–[46] and classification[47]–[49] applications. Evidence theory is a powerful framework for imprecise probability. It works with a discernment framework (DF) Ω={ω1,...,ωc} consisting ofcexclusive and exhaustive status of a variable, the uncertainty and imprecision degree of this attributes are expressed by subsets of the power-set 2Ωwith different basic belief assignments (BBAs), also called mass functions of belief.

In classification problems, the evidential class2In evidence theory, the term evidential refers to variables with both uncertainty and imprecision.of a patternxunder the power-set 2Ωis mathematically defined as a BBA mappingm(·) from 2Ωto [0,1], which satisfies the following conditions:m(∅)=0 and

wherem(A)>0 represents the support degree of the object associated with the elementA. In classification problems,Amay represent singleton class with |A|=1, or meta-class with|A|>1. Ω denotes all elements andm(Ω) is the degree of total ignorance. Total ignorance usually plays a neutral role in the fusion process because it characterizes the vacuous belief source of evidence.

In multiple classifier fusion processing, each classification result can be regarded as an evidence source represented by a BBA, and then the famous Dempster’s rule is used to combine multiple BBAs, which is conjunctive, commutative and associative. The DS combination of two distinct sources of evidence characterized by the BBAsm1(·) andm2(·) over2Ωis denoted asm=m1⊕m2, and it is mathematically defined(assuming the denominator is not equal to zero) bym(∅)=0,and ∀A≠∅∈2Ωby

Often, the probability degrees converted from BBA are applied for decision making over singletons in DF Ω.

There are also a few methods [31], [41], [50] based on evidence theory to deal with incomplete data. For example, a prototype-based credal classification (PCC) method is proposed in [31]. In PCC, the incomplete pattern is edited withcpossible versions, for ac-class problem, to obtaincdifferent classification results by a single classifier. Then thecresults with different weights are fused to obtain the final classification of the incomplete pattern. Although PCC can characterize uncertainty caused by missing values, the estimation strategy also introduces new uncertainty information.Besides, it assumes that the training set is complete.

III. BELIEF COMBINATION OF CLASSIFIERS

This section presents a belief combination of classifiers(BCC) method based on evidence theory for classifying incomplete data. The BCC can faithfully make use of the observed data without imposing any assumption on missing values.

Given anS-dimensional dataset X in class DFΩ={ω1,...,ωc}. Thesth (s∈{1,...,S}) dimension of attributes, denoted

For an incomplete query patternx∈X withHobserved attributes, onlyHclassifiers corresponding to theHobserved attributes could provide reliable results amongSclassifiers.

The calculation of BCC mainly consists of three steps:evaluation of classifier reliability, evaluation of attributes’importance, and the global fusion of classifiers with decisions.

A. Classifier Reliability Calculation

Therefore, a set of equations are constructed as follows:

B. Attribute Importance Calculation

Many works have been devoted to exploring the importance of attributes in various data analysis domains [6]. In this work,the reliability matrix α of classifiers is estimated by a global optimal combination process, which may not apply to some specific patterns. The discounting factors of evidence are also related to the distributions of (missing) attributes of query patterns. As a simple example, Fig. 1 illustrates the distribution of the 1st and 5th attributes for the real dataset,named cloud, from the UCI (University of California, Irvine)repository (available at http://archive.ics.uci.edu/ml).

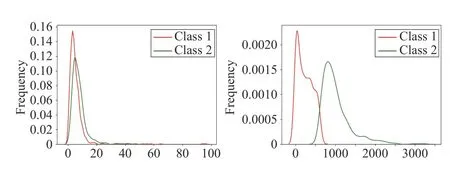
Fig. 1. The distribution of attributes in different classes with cloud dataset.

It can be reported from Fig. 1 that the distributions of the 5th attribute under the two classes are quite different.Therefore, the cross-entropy between the two classes in the 5th attribute is larger than that in the 1st attribute, indicating that the 5th attribute provides more prior information than the 1st one. Therefore, it is reasonable to assign different importance weights to different attributes so that some of the crucial attributes play more decisive roles while those who are not very useful for classification are less influential.

It should be noted that the distribution of missing values for different patterns are different, thus, the local attribute weight also changes depending on the observed attributes ofx. This will be discussed in detail in the next part.

C. Global Combination of Classifiers and Final Decision

The pseudo-code of BCC method is given in Algorithm 1 for convenience.

Algorithm 1: Belief combination of classifiers Require: Training set: ; Test set:; A basic classifier: .Ensure: Class decision results XtrainXtest Xtrain={x1,...,xM}Xtest={x1,...,xN}C 1: function BCC training data , test data S Xst rain 2: Reconstruct the training subsets, ;S Cs 3: Train corresponding basic classifiers, ;4: Construct the reliability optimization equations by (6) and(7);5: Optimize classifier reliability matrix by (10) with constraint of (8);6: Obtain the Pearson product-moment correlation coefficient by (11);7: Calculate local attribute importance by (12);i=1 ρs 8: for to N do 9: Obtain the classification results of with the trained classifiers;xi 10: Calculate the joint discounting factor by (13);ˆγh γs 11: Extract the relative discounting factor by (14a) and(14b);12: Discount these different evidence by (15);13: Fuse these different evidence by (16);14: Classify the query pattern and decide by (17).15: end for 16: return class label 17: end function xi

D. Discussion

1) Selection of Basic Classifiers:Since we focus on improving the accuracy of classifying incomplete data rather than improving the classifier’s performance, any classifier can be employed in principle. However, in the combination process, each observed attribute is considered an independent pattern. In such a case, the patterns used to train the basic classifier are 1-dimensional. Therefore, it is better to choose those general classifiers as benchmarks rather than those designed specifically for high-dimensional data. Most of the conventional classifiers are designed with the framework of probability, so the focal elementAusually represents a specific class under the framework Ω in (7), thereby considering specific classes as an admissible solution of the classification. Nevertheless, there are also some classifiers based on the framework of belief functions [47], which can generate specific classes as well as the total ignorant class Ω.In such a case,m(A) is the belief mass committed to the focal element (class)Ain (15). Of course,pi=p(ωi) is equal tom(A)if the focal elementArepresents the specific class ωiin(7).

2) Selection of Combination Rule:For the selection of combination rule, it is known that numerous combination rules exist dealing with different kinds of evidence resources and conflicts. However, our goal is not to propose a new combination rule but to improve the classification performance by reasonably characterizing the uncertainty and imprecision caused by missing values based on evidence theory when classifying incomplete data. A number of experiments prove that this is feasible. In fact, many combination rules have been proposed when dealing with conflicting evidence, such as Smet’s rule [57], Yager’s rule [58],Dubois-Prade (DP) rule [59] and proportional conflict redistribution (PCR) rules [60].

The property of associativity is important in our application since the fusion of multiple evidences are calculated in a sequential way in which the order makes no difference. The above rules are not associative, which makes them less attractive in applications. High conflict within evidence sources is another issue in information fusion which often makes results hardly reliable. By considering these two issues,in our method, the sources of evidence are firstly modified to prevent (possible) highly conflicts, and then combined by the Dempster’s rule to determine the final class of query patterns.Based on the Shafter’s discounting method, the whole conflicts are distributed to total ignorance Ω due to normalization when different evidences are highly conflicting or in some special low-conflict situations.

IV. EXPERIMENT APPLICATIONS

To validate the effectiveness of BCC method confronting missing data, a number of benchmark datasets are employed to compare with several other conventional methods based on four common criteria: 1) accuracy (AC); 2) precision (PE); 3)recall (RE); 4) F1-measure (F1) [61].

A. Methods for Comparison

The classification performance of this new BCC is evaluated by comparisons with several other conventional methods including mean imputation (MI) [22],K-nearest neighbors imputation (KNNI) [23], fuzzyc-means imputation(FCMI) [24], prototype-based credal classification (PCC) [31],fuzzy-based information decomposition (FID) [25], generative adversarial imputation nets (GAIN) [29] and batch Sinkhorn imputation (BSI) [26]. In MI, the missing values in the training set are replaced by the average values of the same class, and the missing values in the test set are imputed by the means of the observed values of the position in the training set. In KNNI, the incomplete pattern in the training set is estimated by the KNNs with different weights depending on the distance between the pattern and the neighbors in the same class, and the incomplete pattern in the test set is estimated by the global KNNs. Since the training set is complete by default in FCMI, PCC, and FID, we thereby use the average values of the class to impute the missing values in the training set,similar to MI. In FCMI, the missing values in the test set are imputed according to the clustering centers generated by FCM and the distances between the object and the centers. In PCC,the incomplete pattern in the test is imputed withcpossible versions for ac-class problem, while the centers ofcclasses are obtained from the training set. In FID, the missing values in the test set are estimated by taking into account different contributions of the observed data. In GAIN, generative adversarial nets are trained to estimate the missing values in the test set. In BSI, the missing values in the test set are imputed by minimizing optimal transport distances between quantitative variables. For all parameters of the compared methods, we use the default values as in the original papers.

Different from the above methods, the proposed BCC considers each attribute as an independent source, and the collection of each attribute is considered as a subset.Afterward, each subset trains a classifier independently, which allows each observed attribute to provide a sub-classification result for the query pattern. Then these sub-classification results with different weights (discounting factors) are used to provide supplementary information to jointly determine the final classes of query patterns.

B. Basic Classifiers

In our simulations, K-NN technique [62], evidentialKnearest neighbor (EK-NN) [47] and Bayesian classifier(Bayes) [21] are employed as the basic classifiers to generate pieces of evidence. In the Bayesian classifier, Gaussian distributions are assumed for each attribute. For the parameters in the classifier, we apply the default values identical to the original papers. The outputs of EK-NN are BBAs consisting of the singletons and the total ignorance, and the outputs of K-NN and Bayesian classifiers are probability values. Both BBAs and probability can be directly applied to the optimal combination in the BCC method as explained in Section III-D.

C. Benchmark Datasets

Twelve datasets from the UCI repository are used to evaluate the effectiveness of BCC with comparison to main conventional methods. The basic features of these datasets are shown in Table I, including number of classes (#Class),number of attributes (#Attr.) and number of instances (#Inst.).The size of each dataset is defined by the number of its attributes (#Attr.) and the number of instances (#Inst.).

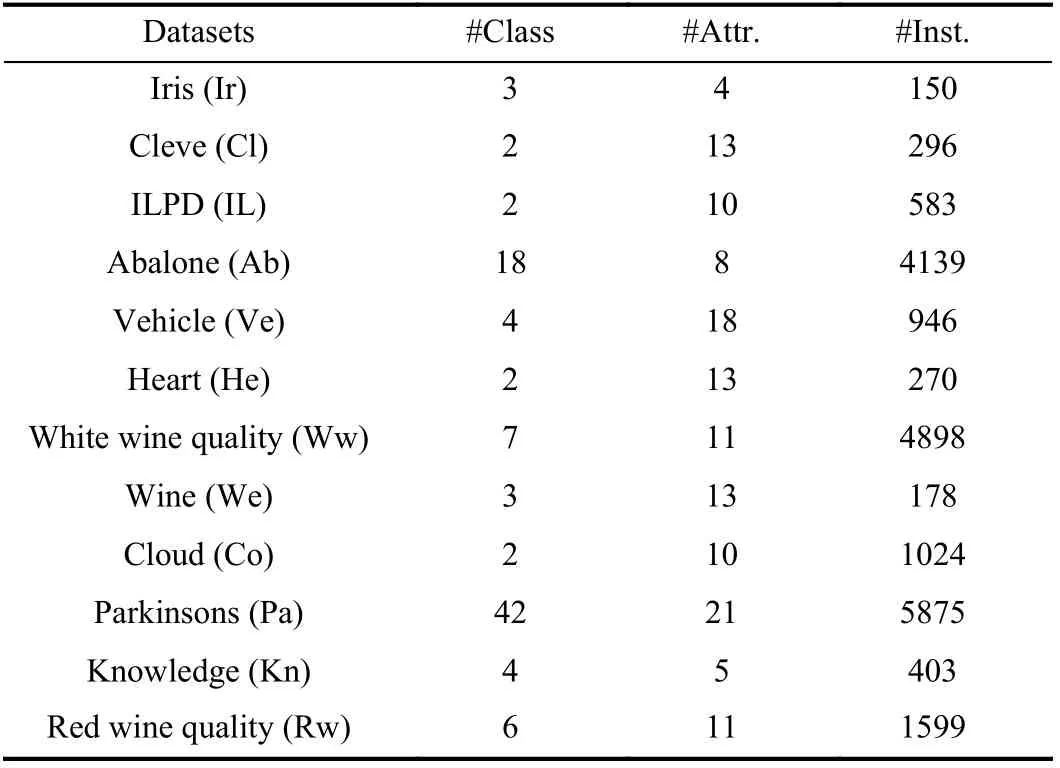
TABLE I BASIC INFORMATION OF THE USED DATASETS

In the experiments, each attribute independently reconstructs a subset and trains a basic classifier. In order to demonstrate the effectiveness under different incompleteness levels, in the training and test sets, we assume that each pattern has φ missing (unobserved) values with missingcompletely-at-random mechanism. In experiments, different values of φ are employed to verify the performance of the BCC method.

D. Performance Evaluation

We use the simplest 2-fold cross validation. Since the size of the training and test sets are equal, all patterns can be respectively used for training and testing on each fold. The program is randomly run 10 times5All results demonstrated in this paper are average values., and the performance of BCC is shown for various φ, denoting the number of missing values for each training and test pattern, as reported in Tables II–VII. Specifically, the accuracy values (AC) for the compared methods, based on K-NN, EK-NN and Bayesian basic classifiers6The differences between the chosen classifiers are beyond this paper., are respectively reported in Tables II, IV and VI. Other indexes, PE, RE, F1, are recorded in Tables III,V, and VII, with K-NN, EK-NN and Bayesian basic classifiers integrated respectively. In Table III, taking the Cl dataset as an example, PE is the average value with different φ ( φ = 4, 6,8 in Table II), based on the K-NN classifier. In addition, the average histograms for φ with different datasets and basic classifiers are plotted in Fig. 2 to compare the effectiveness of BCC more intuitively.y-axis represents the accuracy,calculated by the average of the outputs with different φ in Tables II, IV and VI.

From these results, it can be observed that the BCC method generally provides better results compared to other conventional methods in most cases. Moreover, these results support us to make the following analysis.

As typical single imputation strategies, MI, KNNI, and FCMI predict possible estimations of missing values based on different mechanisms, but such estimations may not be reasonable enough. For example, in KNNI, similar patterns(neighbors) are employed to impute missing values. In this case, the selection of similarity measure norm is an essential process. If an inappropriate measure is chosen, unsatisfactory results are often obtained. Moreover, the disadvantage of direct modeling of missing values is that it is impossible to avoid bringing new uncertainties because estimation can never replace the real world. Furthermore, only modeling missing values is insufficient because the uncertainty caused by missing values can also negatively affect the classifier’s performance. Therefore, we can see that the results obtained by these methods are often not satisfactory.

PCC and GAIN are multiple imputation strategies, which means that a missing value may be estimated as multiple versions to characterize the uncertainty. This is an improvement and reasonable in some ways, however, multiple estimations are not always better than single estimation strategies [63]. In particular, as an imputation strategy, GAIN models the uncertainty of missing values but still does not characterize the uncertainty and imprecision in the model and results from a classification perspective. On the other hand, as an evidence theory-based method, PCC is similar to the proposed BCC method in characterizing the uncertainty andimprecision caused by missing values. However, in PCC, the use of class centers as a benchmark for estimating missing values is unreasonable and does not assess the reasonableness and necessity of multiple estimations. Therefore, it can characterize the imprecision in the results, but the performance is still not good enough.

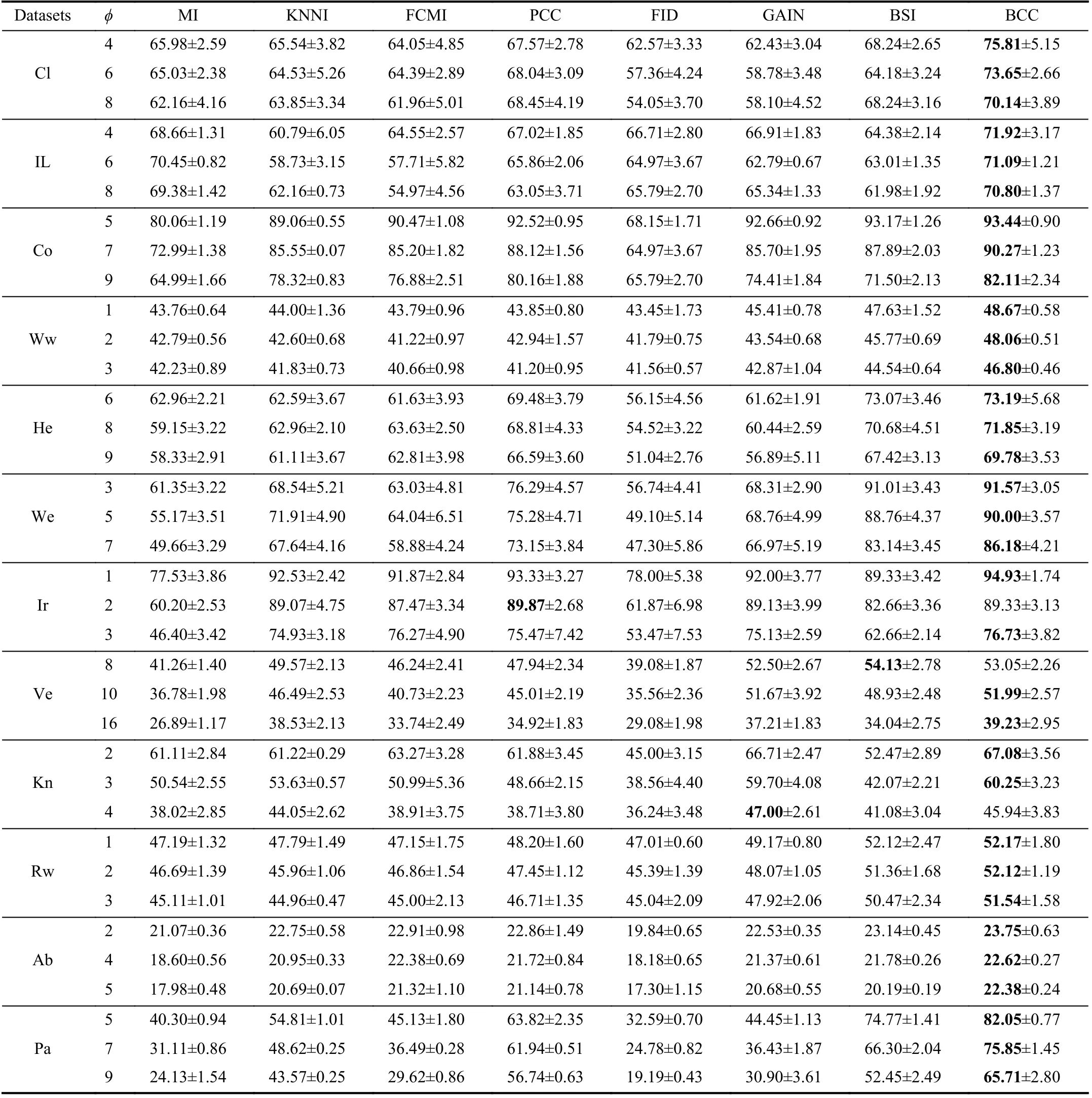
TABLE II THE ACCURACY (AC) OF DIFFERENT METHODS WITH K-NN CLASSIFIER (%)

As the latest work, FID, GAIN, and BSI have proposed some feasible solutions from data distribution but only partially address the problem of modeling incomplete data.For example, GAIN and BSI, as model-based methods, are dedicated to perfectly approximating the real world, which is practically impossible. In particular, BSI assumes that two random batches from the same dataset should follow the same distribution. Still, in some scenarios, the distribution of the data itself is hard to estimate. If the data distribution is not modeled precisely enough, the reasonableness of the estimations is questionable. FID is a pioneering work that works on both incomplete and imbalanced data classification.In FID, the imbalance is also considered incomplete data, so its essence is still a classification of incomplete data.However, the classification results are also less than ideal because the process does not reasonably characterize theuncertainty and imprecision caused by missing values.

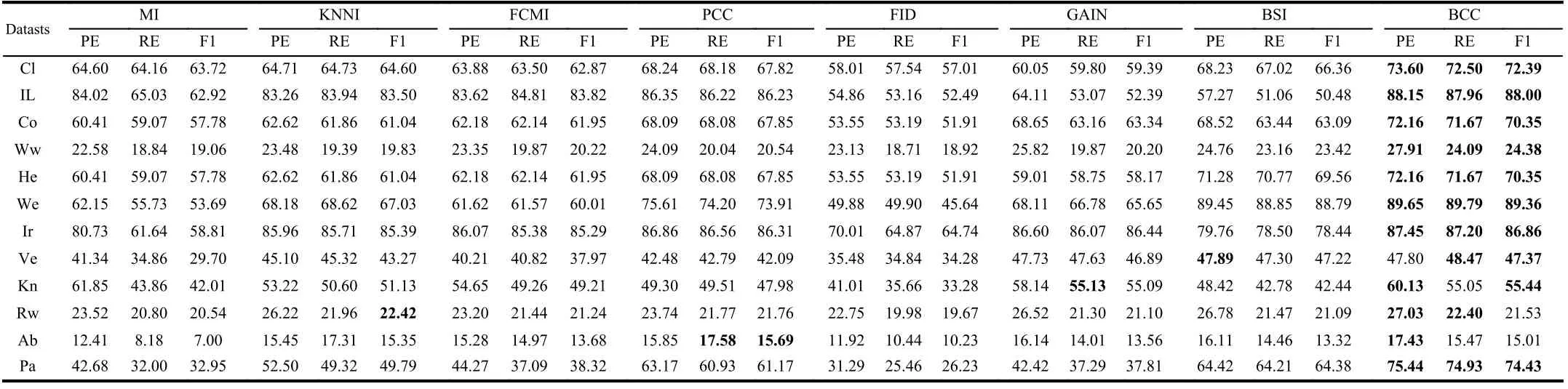
TABLE III THE PE, RE AND F1 OF DIFFERENT METHODS WITH K-NN CLASSIFIER (%)

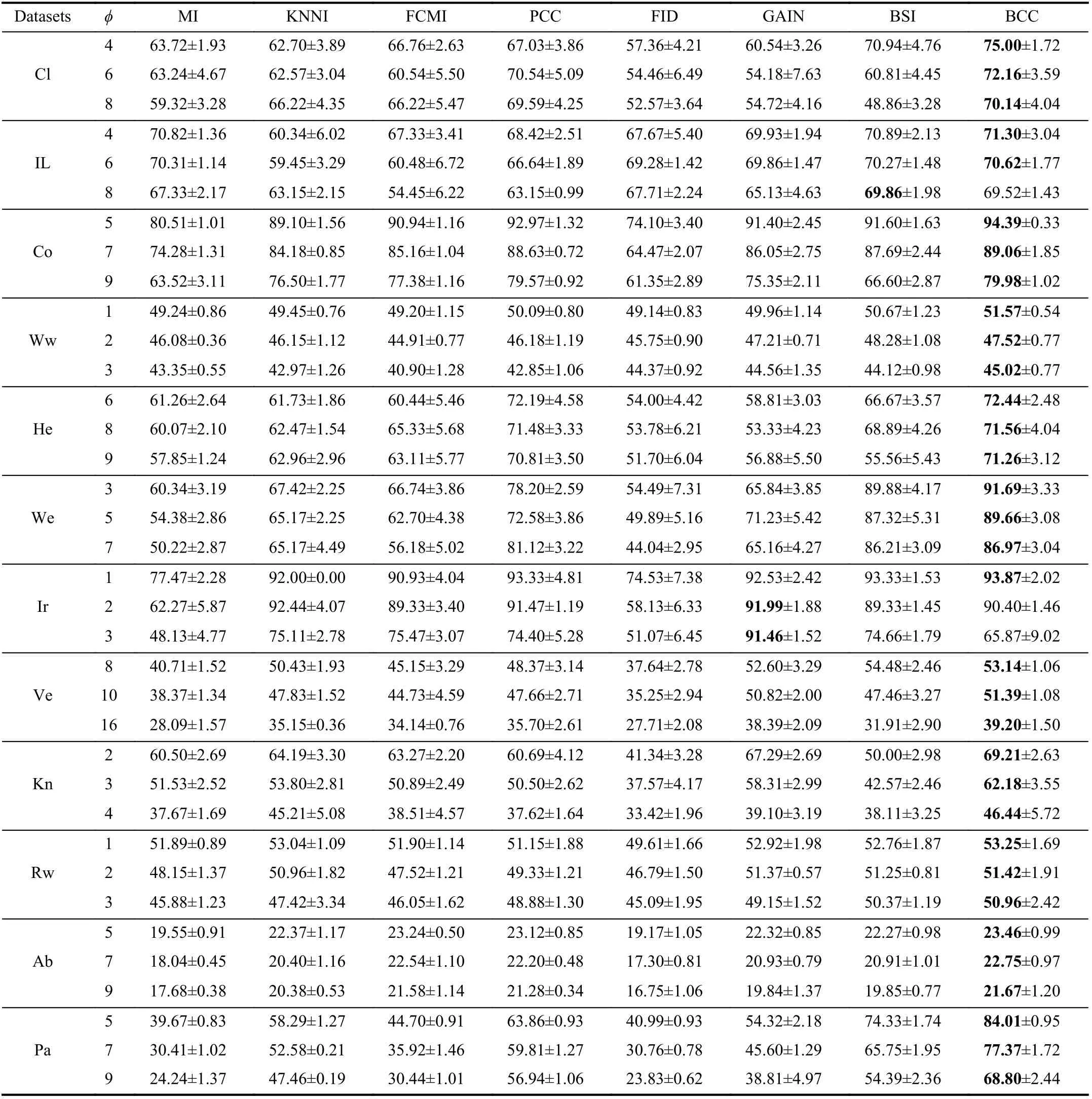
TABLE IV THE ACCURACY (AC) OF DIFFERENT METHODS WITH EK-NN CLASSIFIER (%)

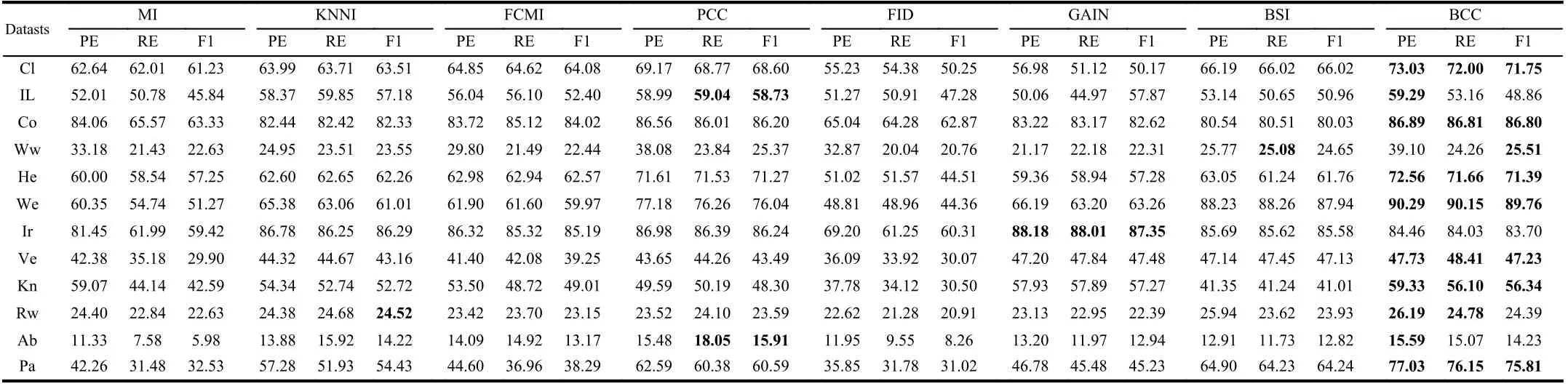
TABLE V THE PE, RE AND F1 OF DIFFERENT METHODS WITH EK-NN CLASSIFIER (%)

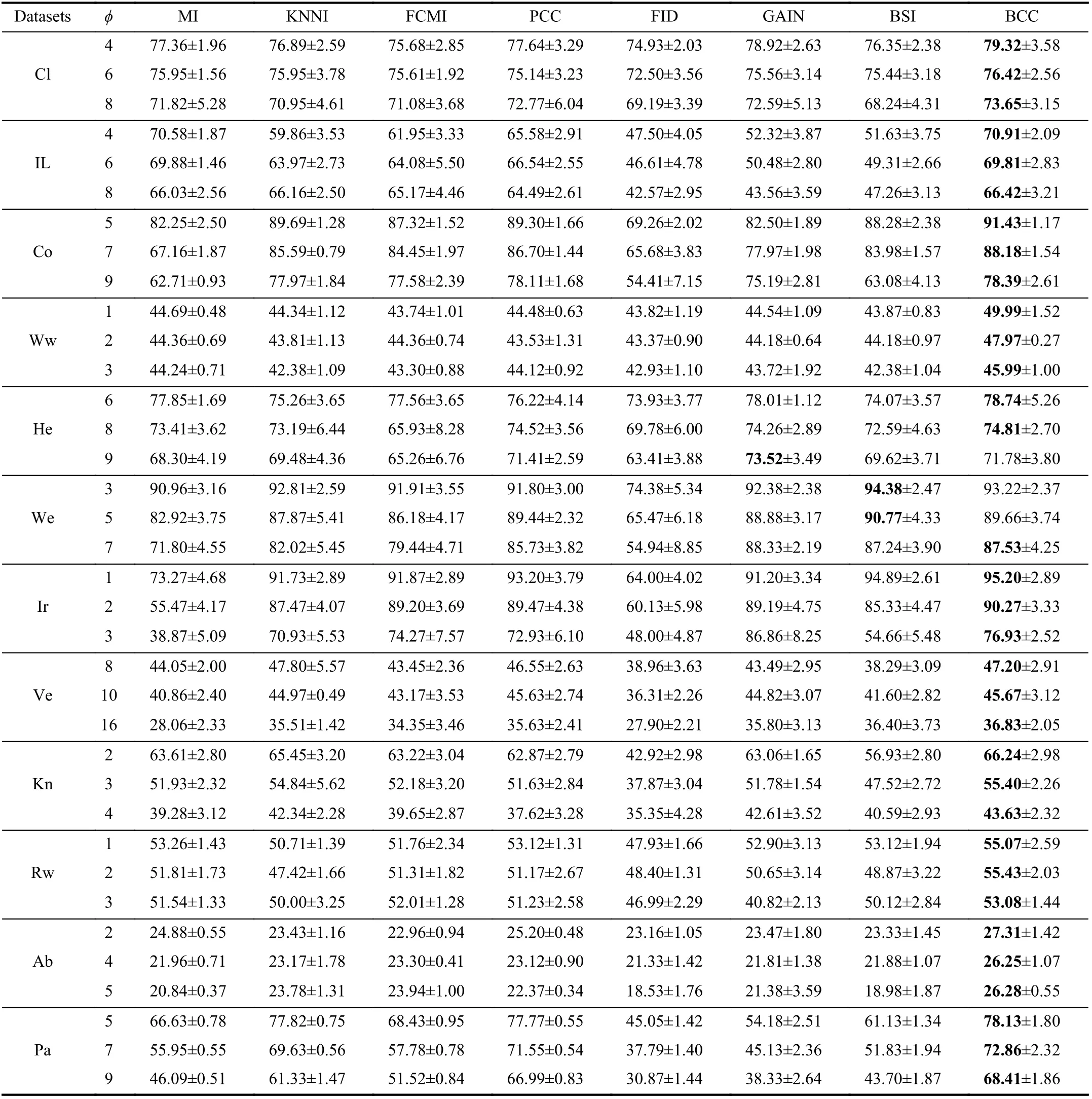
TABLE VI THE ACCURACY (AC) OF DIFFERENT METHODS WITH BAYESIAN CLASSIFIER (%)

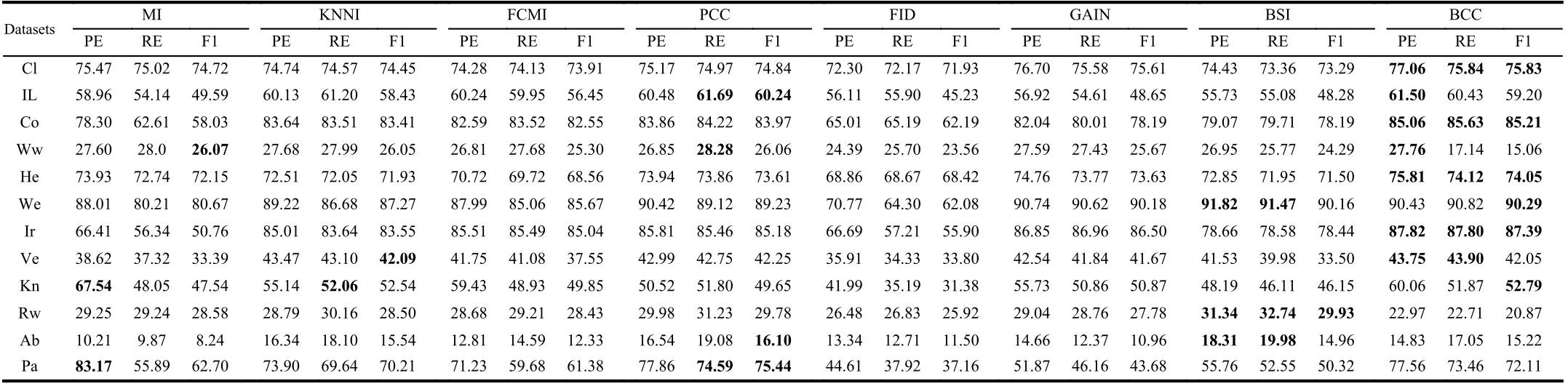
TABLE VII THE PE, RE AND F1 OF DIFFERENT METHODS WITH BAYESIAN CLASSIFIER (%)

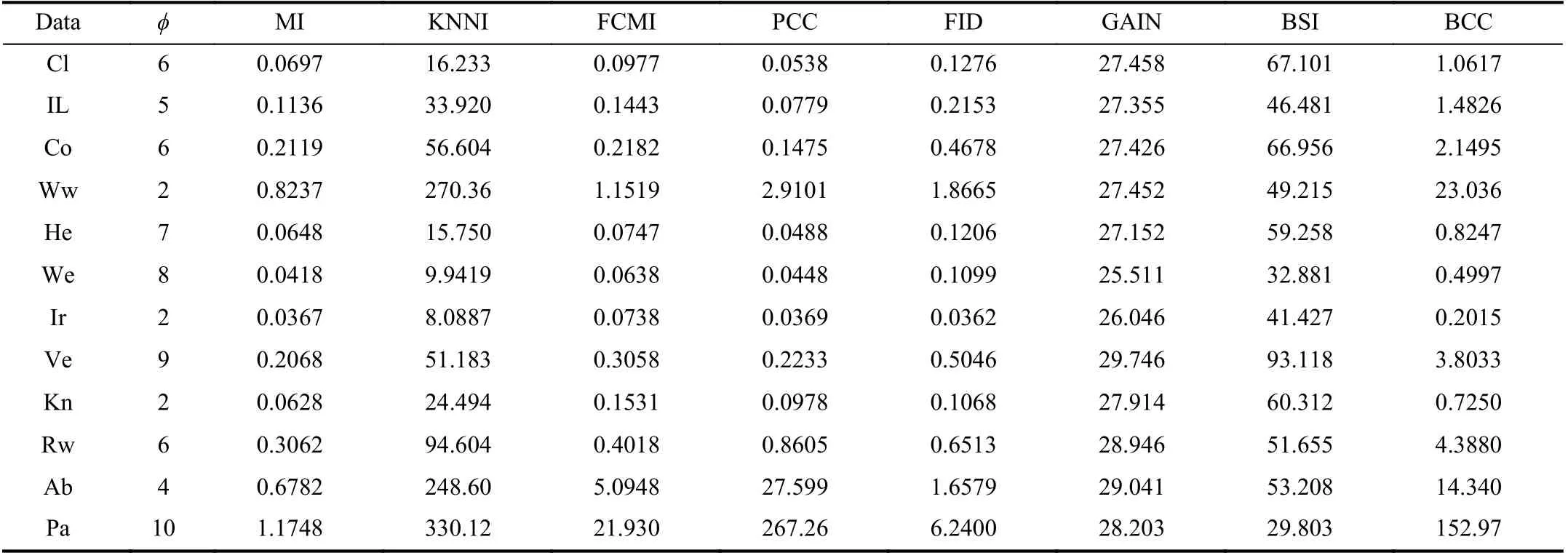
TABLE VIII EXECUTION TIME WITH K-NN CLASSIFIER (S)

The proposed BCC method avoids modeling missing values directly. Thus, it can handle well the cases where both the training and test sets contain many missing values without losing information and introducing new uncertainty information. We model each attribute independently while avoiding negative interactions between attributes.Simultaneously, different attributes are able to provide complementary information under the framework of evidence theory. By doing this, the distribution characteristics of different attributes are thoroughly mined, and each attribute can train a basic classifier independently. Moreover, the performance of the classifiers depends on the quality of the training sets constrained by missing values. In this case, the global measurement of the weight on each classifier is an important part of making decisions as cautious as possible. In addition, the proposed BCC method is end-to-end, which can characterize the uncertainty and imprecision in the data, the model, and the results simultaneously. Therefore, the proposed BCC is often able to outperform other comparison methods.

Furthermore, from Fig. 3, it can be observed that the accuracy is less affected by the data incompleteness level for BCC than other methods, indicating that BCC is more robust.Indeed, the BCC can be regarded as an intermediate of multiple classifiers, effected by the combination process.Since the incompleteness is characterized by imprecision rather than uncertainty in evidence theory, the imputed values make less impact on the classification results than other methods, realized by the Dempster’s combination rule. Such a mechanism brings robustness to the BCC method.

In addition, we can also observe that with the increase of φ,the classification accuracy results of different methods decreases in most cases. This is consistent with our intuitive perception, because a larger φ implies the loss of more attributes from a pattern. The less information the pattern contains, the more difficult it is to classify the pattern correctly, the classification accuracy thereby gradually declines. However, the performance of BCC is still better than that of other conventional methods in the same case. In addition, the increase in φ also reflects the increase in the proportion of missing from another perspective. For example,if φ = 9, for the Cloud dataset, the missing rate of the training and testing sets is 90%.

We admit that a few issues exist in BCC, one of which is the computational cost. Since BCC is a combination mechanism of multiple classifiers, it is less efficient than a single classifier. Thus, the satisfactory results are obtained at the cost of more computational resources. Another potential issue is the combination step. The Dempster’s rule is applied to combine multiple classification results. When high conflicts still exist between discounted evidence, the rule may return an undecidable BBA. In this case, the issue becomes nonnegligible.

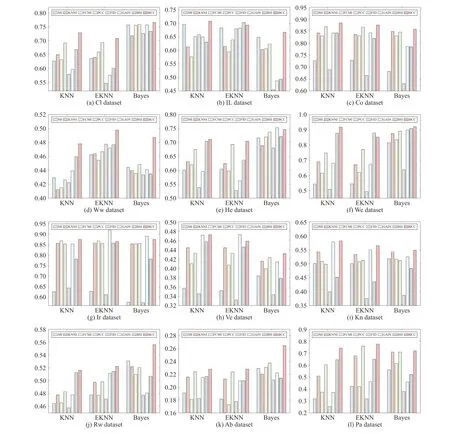
Fig. 2. The average accuracy (AC) of different methods in various datasets.

E. Computational Cost

The execution time of the different methods with K-NN as the basic classifier is shown in Table VIII. It shows that the BCC method is indeed more time-consuming than other methods since BCC needs to spend more time training the basic classifier and optimizing the discounting factors of pieces of evidence. However, the computational cost is much less than KNNI, GAIN and BSI methods in most cases, for example, for KNNI, because searching for neighbors is a very time-consuming task as the number of patterns increases.Therefore, it is necessary to take a trade-off between performance and computational cost when using the BCC method. Generally speaking, BCC is more suitable for applications in which high classification accuracy is required whereas efficient computation is not a strong requirement.

V. CONCLUSION

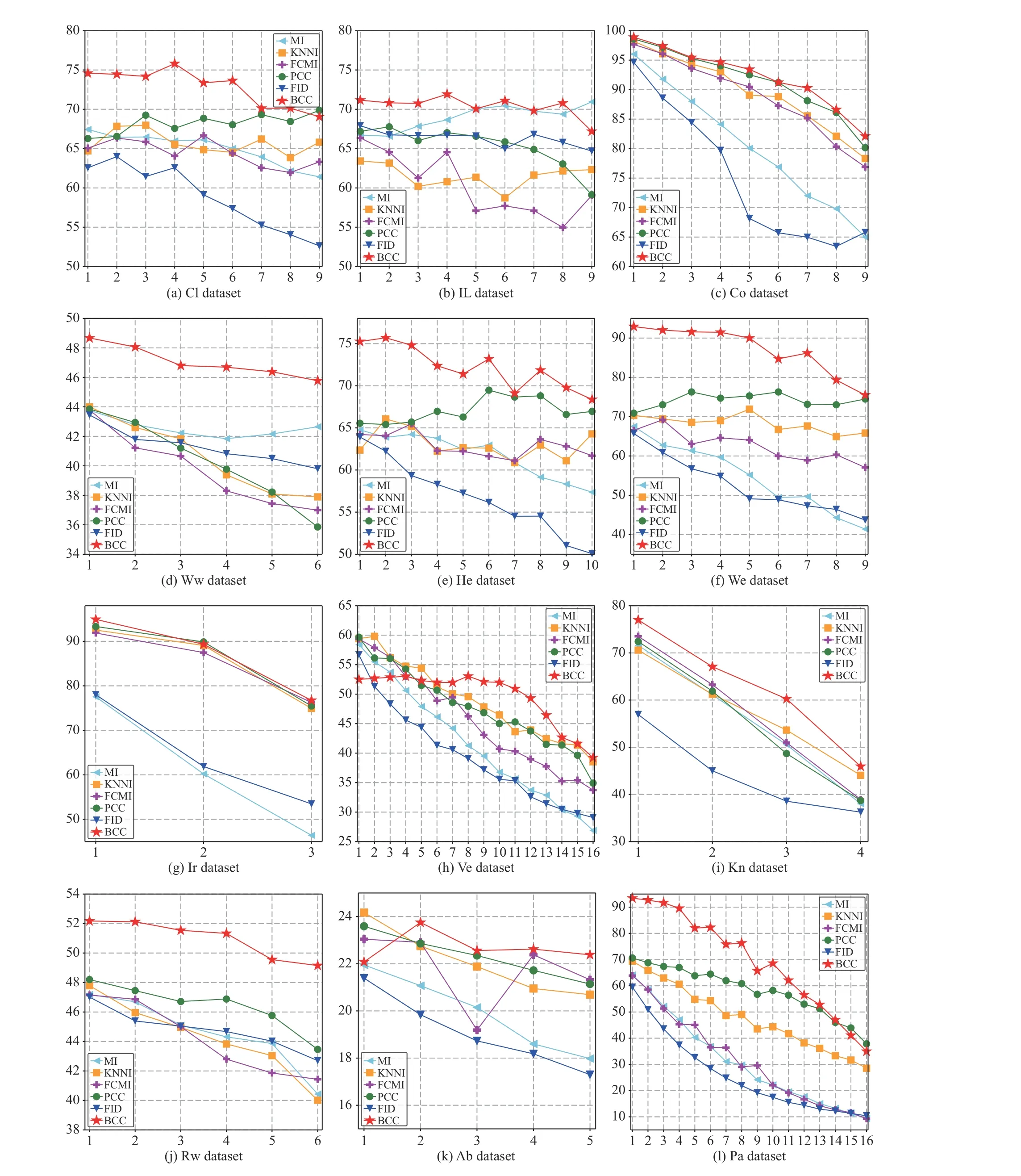
Fig. 3. The effect of parameter φ on average accuracy (AC) within different methods over various datasets. The horizontal and vertical axis respectively represents the value of parameter φ and AC.

Confronting the problem of classification over incomplete data, we proposed a new belief combination of classifiers(BCC) method in the framework of evidence theory under the fact that patterns in the training set and test set are incomplete.The BCC method characterizes the uncertainty and imprecision caused by missing values with the theory of belief functions. By doing so, BCC is able to make full use of observed data while introducing little impact in dealing with missing data. Consequently, it outperforms conventional classification methods for incomplete data. The core action of BCC is to construct attributes as independent sources, and each of them is used to train a classifier and thereby predict the class of query patterns. As a result, multiple outputs with different discounting factors for the query pattern are obtained. The discounting factor includes two parts: the global classifier importance and the local attribute reliability, with which the famous Dempster’s rule is employed to fuse the discounted pieces of evidence representing evidential subclasses and then determine the final belief classification for the query patterns. The effectiveness of BCC is demonstrated using various real datasets by comparisons with other conventional methods. The experimental results show that BCC significantly improves the performance in accuracy,precision, recall, and F1 measure. Furthermore, this new method is robust since it does not need to set parameters manually, making it convenient for practical applications.

In recent methods, missing values are usually imputed by value approximation, significantly affected by deep learning approaches. However, the lack of robustness caused by overfitting and under-fitting issues has been an obstacle in applying these theoretical methods. The proposed BCC method makes a step forward by taking decisions between specific classes and total ignorance. However, it cannot yet characterize local imprecision [31], [50]. To conclude, the mathematical method given in this paper can somewhat reveal the hidden real world from missing data. In the future, we will employ these classifiers specially designed for highdimensional data, and we will explore applying a similar methodology to more missing data scenarios beyond the conventional classification. Concerning the robustness problem caused by data missing, a more general framework managing uncertainty and imprecision adaptable to various learning tasks with incomplete patterns is also in the scope of our future work.