Atomic Spin Polarization Controllability Analysis:A Novel Controllability Determination Method for Spin-Exchange Relaxation-Free Co-Magnetometers

Zhuo Wang,, Sixun Liu, Ruigang Wang, Linlin Yuan, Jiong Huang, Yueyang Zhai, and Sheng Zou

Abstract—This paper investigates the atomic spin polarization controllability of spin-exchange relaxation-free co-magnetometers(SERFCMs). This is the first work in the field of controllability analysis for the atomic spin ensembles systems, whose dynamic behaviors of spin polarization are described by the Bloch equations. Based on the Bloch equations, a state-space model of the atomic spin polarization for SERFCM is first established,which belongs to a particular class of nonlinear systems. For this class of nonlinear systems, a novel determination method for the global state controllability is proposed and proved. Then, this method is implemented in the process of controllability analysis on the atomic spin polarization of an actual SERFCM. Moreover,a theoretically feasible and reasonable solution of the control input is proposed under some physical constraints, with whose limitation of realistic conditions, the controller design can be accomplished more practically and more exactly. Finally, the simulation results demonstrate the feasibility and validation of the proposed controllability determination method.

I. INTRODUCTION

QUANTUM information technology has been the new main trend of information science and technology under the promotion of quantum mechanics and information technologies since the beginning of the 21st century [1]–[4].Quantum precision measurement is one of the research directions closest to practical application as an important branch and research hotspot in the field of quantum information technology [5], [6]. The precision measuring instruments based on effects of atomic spin have become various types of indispensable equipments such as atomic clocks [7], atomic magnetometers [8], and atomic comagnetometers [9], etc., for exploration on the leading science research frontiers by utilizing the characteristics of fine structures and quantization of transitions of atomic energy levels, where atomic co-magnetometer can be divided into two categories: the nuclear magnetic resonance gyroscopes(NMRG) [10] and the spin-exchange relaxation-free comagnetometers (SERFCM) [11] according to their different working principles.

Alkali metal atoms within the cell of SERFCM may reach the SERF regime by the synthetic effects of high temperature and pump beam, in which the effect of polarization from spinexchange rate is far greater than Larmor precession’s, for hyperpolarizing the noble gas atoms. In the SERF regime, the signal intensity and signal-to-noise ratio are enhanced significantly as the improvements of atomic spin relaxation times, coherence and density. Furthermore, there is an interaction between electron and nuclear spin that can trace and compensate the slight fluctuation of the ambient magnetic field such that the high sensitivity for rotation sensing can be achieved in the SERF regime. Thus, SERFCM can not only be applied in inertial navigation as a promising gyroscope with high-performance [12], [13] but also serve for exploration in fundamental physics, for example the test of CPT and Lorentz violation [14]–[17], as well as searches for spin-dependent forces [18], [19].

The spherical cell almost filled with alkali metal vapors as well as the noble gas is a key component used in SERFCM for rotation sensing, and the dynamical evolution of spin polarization of these atoms within the cell can be described by a set of partial differential equations (PDEs) called the Bloch equations [17], which play an important role for interpreting the principles and characteristics of SERFCM. However, it is hard to obtain the complete analytical solution with respect to the time of such complicated PDEs. In this case, besides a series of theoretical and dynamic analyses [20]–[22], relevant studies put the main focus on practical engineering and always research the suppression or optimization for some kinds of perturbation and performance indexes based on the steadystate solution. For instance, the studies of magnetic noiseinduced rotation measurement error [23], cross-talk effect in the dual-axis co-magnetometers [24], fluctuation of pumpbeam intensity [25] and influence of the cell temperature [26]are always hotpots. It is worth noting that there are scholars who recently have introduced the data-driven state observation (DDSO) method for estimating the nuclear spin polarization in real time [27]. We believe that the organic combination of control theory and SERFCM is one of the unneglected future directions but underestimated now, and this work above exactly demonstrates the potential for this kind of combination.

So far, there has been few works focusing on the studies of SERFCMs from the perspective of control theory, which were concentrated on stability analysis, like long-term stability[28], [29] and bias stability [30], [31], and the studies on properties of SERFCMs involving controllability and observability in control domain were rarely reported,especially lacking on issues related to controllability. The concept of controllability emerged with the proposition of the state-space method in the 1960s for studying whether the systems can be controlled effectively or not by control input[32]. In general, the Bloch equations can be applied directly as the state-space model of SERFCMs in which the state vector contains the polarization of atomic spin ensembles.Nevertheless, the existing controllability determination method is not feasible for this system model of SERFCM because of its high nonlinearity and unqualified system features [33]–[36]. Under this situation, there are two distinct approaches: one way is to simplify the nonlinear model to a linear system directly for reducing the analysis difficulty, but excessive elimination of nonlinear terms may cause a startling deviation between the results we derived and reality; another way is to appropriately simplify the Bloch equations to the nonlinear system with a specific form or any other characteristics, then design the corresponding controllability analysis methods from its form and characteristics. Actually,the new controllability determination method proposed in this paper is exactly based on the second approach.

In the research field of SERFCM, there is no report on the atomic spin polarization controllability, which follows that the theoretical results in this paper are pioneering and groundbreaking. Furthermore, though the study object in this paper is SERFCM, the research idea on the controllability of the atomic spin ensembles systems, whose dynamic behaviors are described by the corresponding Bloch equations, has genuine generality. Therefore, our conclusions have certain universality and potential to be expanded to other precision measuring instruments, whose working principles are based on the effects and dynamical evolutions of the atomic spin described by the Bloch equations.

The structure of this paper is as follows. Section II derives the atomic spin polarization model from the Bloch equations,which is a nonlinear system in nature with a specific form. For this class of nonlinear systems, Section III proposes and proves the criterion condition of global state controllability.Section IV demonstrates the controllability analysis process for an actual SERFCM. Section V verifies the validation of our new controllability determination method by the numerical simulation of the K-3He SERFCM. Finally,conclusions are drawn in Section VI.

II. ATOMIC SPIN POLARIZATION MODEL OF SERFCM AND ITS CONTROLLABILITY PROBLEM

These solutions will agree well with previous studies (3)and (4) if we further simplify (9) and (10) by neglecting small terms, it follows that the model we established is applicable for SERFCM. Moreover, the precision of estimation results for longitudinal electron and nuclear spin polarization are improved explicitly in comparison with previous studies.

The electron polarization of alkali metal and the nuclear polarization of noble gas play a significant role in the establishment of the theoretical model of SERFCM and they can describe the performance explicitly. The nature of the atomic spin polarization model (6) of SERFCM is a nonlinear system with a specific form and it is necessary for us to analyze its controllability theoretically.

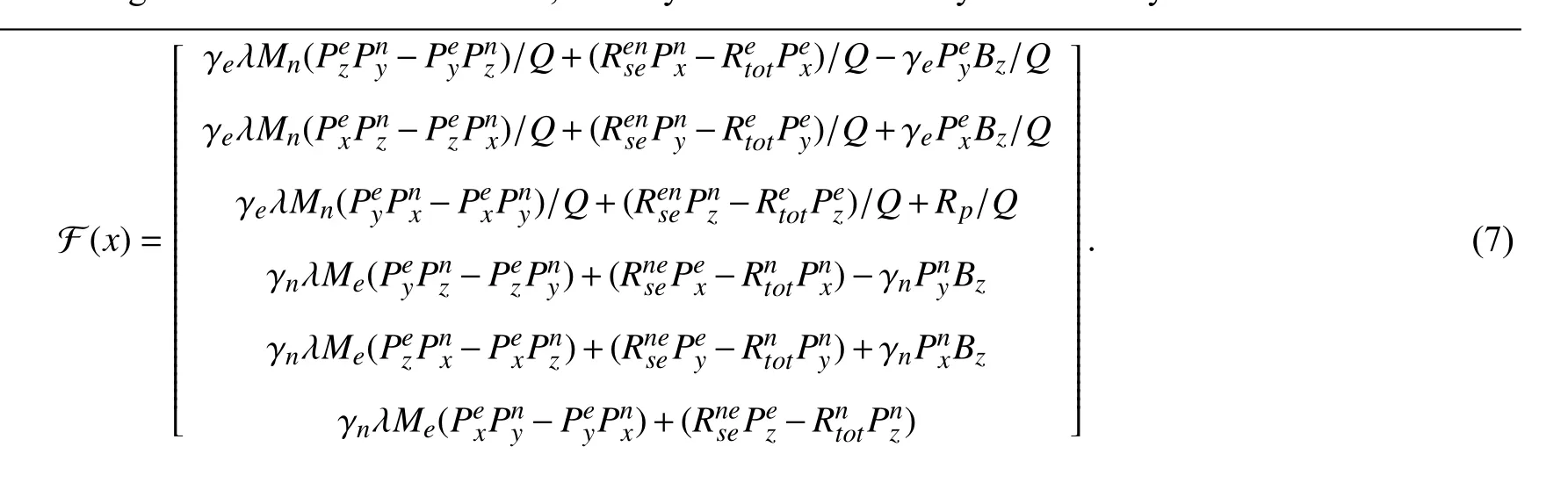
III. PROPOSED CONTROLLABILITY DETERMINATION METHOD

In this section, the criterion condition for controllability and corresponding proof are proposed for analyzing the nonlinear system (6).

A. Preliminaries

B. The Controllability Determination Method for a Particular Class of Nonlinear Systems

Under Assumption 1, system (11) can be rewritten as follows:

The analytical solution of partial differential equation (12) is given as follows:

From (18) and (19), we can deduce that

IV. ATOMIC SPIN POLARIZATION CONTROLLABILITY ANALYSIS FOR SERFCM USING THE PROPOSED METHOD

As we mentioned before, the Bloch equations can be rewritten as a nonlinear system with the specific form while SERFCM is considered at PSS. For this class of nonlinear systems, a novel controllability determination method is provided, which can be applied to analyze the atomic spin polarization controllability for SERFCM.

The validation of the controllability determination method we propose in this paper is based on Assumption 1, thus we need to verify whether system (6) satisfies Assumption 1 or not at first.

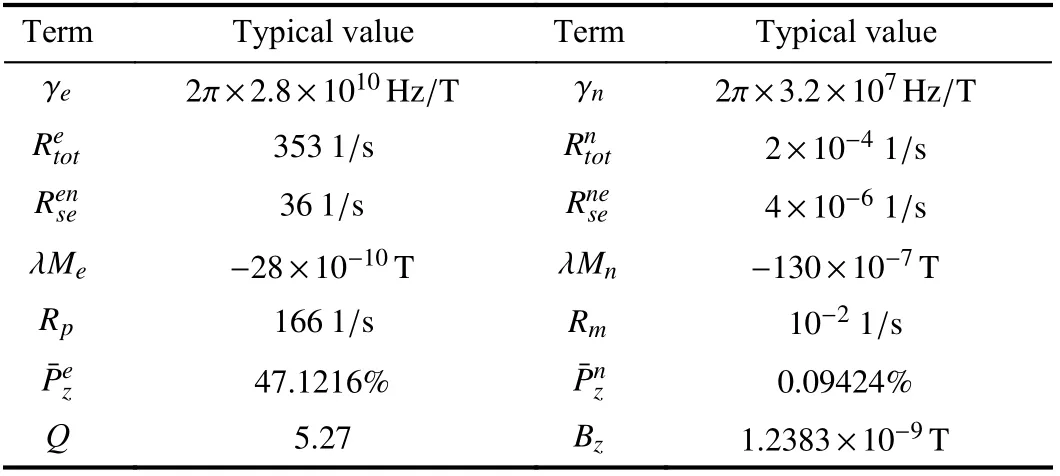
TABLE I¯P ez¯P nz TYPICAL VALUES [17] FOR SERFCM BASED ON K-3HE ATOMIC SOURCE AT PSS, WHERE THE LONGITUDINAL POLARIZATIONS AND ARE CALCULATED BY (9) AND (10), RESPECTIVELY. THE POLARIZATION-DEPENDENT SLOWING-DOWN FACTOR IS CALCULATED BY DEFINITION. WE IGNORE THE LIGHT-SHIFT L AND THE MOST RELEVANT ROTATIONS ARE THOSE OF THE EARTH

Consequently, with the further study around SERFCM, the atomic source schemes can be foreseen to involve more and complicated combinations, and the check for the full rank property ofScis necessary while the controllability determination method this paper provided is applied to the polarization controllability analysis for SERFCM based on kinds of atomic sources in practical engineering.

Remark 4:Throughout this paper, the achievement of global state controllability for SERFCM is based on a basic assumption that PSS is kept during the whole operation or control process, which can be interpreted from these perspectives below.

1) Considering the system (6) from the perspective of control theory, although the bounded initial statex0can be transferred to any bounded terminal statexTin the state-space R6, the state trajectoryx(t), wheret∈[0,T], must satisfy those criterion conditions (5).

2) From another perspective, in practical engineering, as the high-sensitivity property of SERFCM for rotation and magnetic field sensing, the electron and nuclear spin polarization vary rapidly and significantly while the impacted excitations, like an unexpected magnetic field or high rotation rate, are employed, it is not until the absence of excitations that SERFCM can restore to PSS, which is always taking a long time.

Therefore, even if we have acquired the results of controllability for various SERFCMs, the magnitudes of‖u(t)‖and ‖∂Pez/n/∂t‖ from state trajectory still need to be considered carefully while we design the controller.

Remark 5:Besides SERFCM, there are many precision measuring instruments based on effects of atomic spin, like SERF magnetometer [40] and NMRG [41], their working principles can be described by different forms of Bloch equations, which implies that our research has potential to be generalized to theoretical models of them.

V. NUMERICAL SIMULATION

Considering an SERFCM based on K-3He atomic source,the relevant typical values are shown in Table I, and their global state controllability has been analyzed and proved in Sections 3 and 4.

Set the initial state and the expected terminal state as follows:

Fig. 1. A feasible but non-exclusive control input u(t)=[Bx By Ωx Ωy]T for transferring the initial state x0 to the expected terminal state xT. In order to keep SERFCM system at PSS, (5) and (27) must be satisfied, such that the control input must be a slowly time-varying smooth function.

Remark 6:When the dynamic model of an SERFCM does not satisfy the criterion condition proposed in Theorem 1.

1) One can first analyze the degree of controllability and determine the uncontrollable state components, to find whether there exist some hardware means to change the structural characteristics of the system, for the sake of making the system completely state-controllable. In practical engineering,for SERFCM, its system structural characteristics are basically determined by the core sensitive component, i.e., the vapor cell. Thus, the uncontrollability and instability of the system

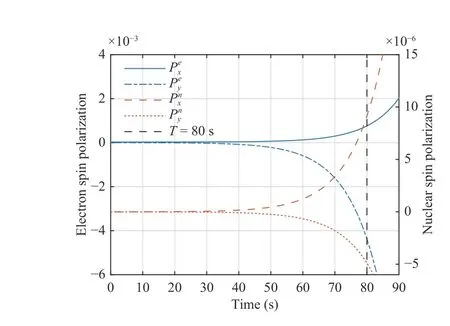
Fig. 2. The polarization trajectory under the control input u(t).Eventually achieve with the transition time T =80 s.

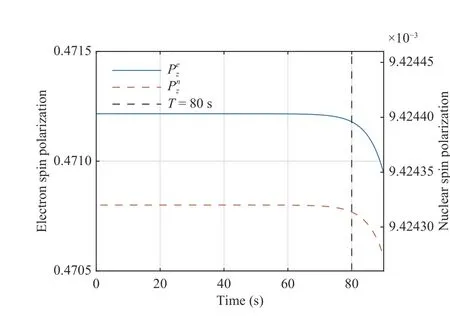
Fig. 3. The longitudinal spin polarization varies slightly with the variation of input u(t), which implies that the fluctuation of the equilibrium point is inevitable when any control measure is implemented on SERFCM system.

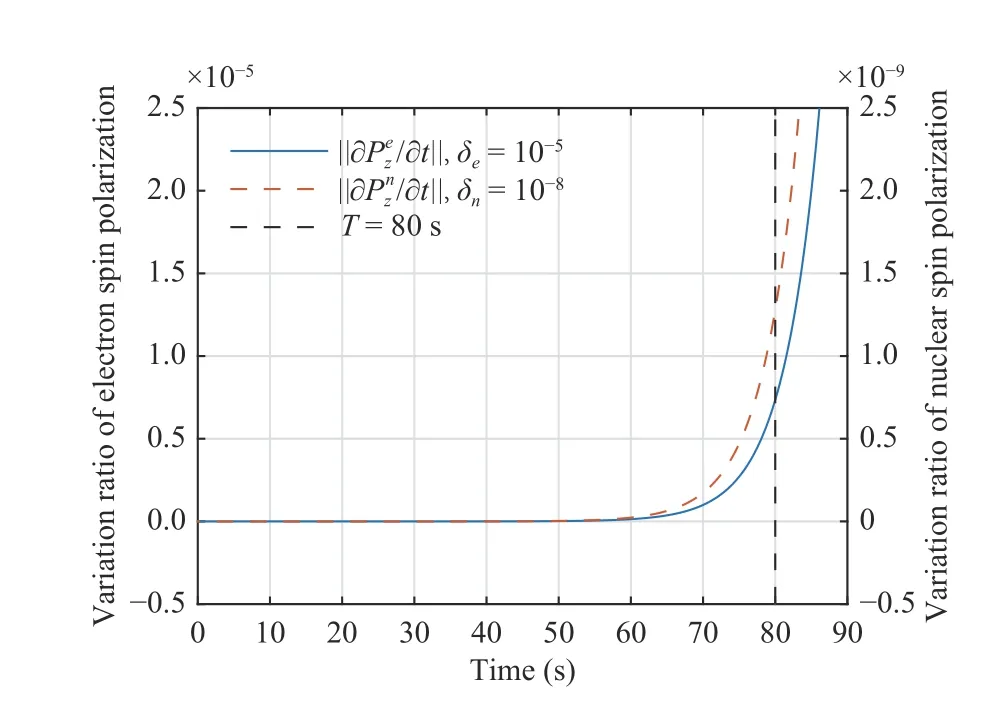
Fig. 4. with su tp<δe/n satisfied, which agrees well with the basic assumption that SERFCM system is at PSS during time interval [0,T].This demonstrate that the control input u(t) in Fig. 1 is feasible and applicable.

indicate that the performance parameters of the vapor cell,such as the atomic source combination, the density ratio, and the inner pressure, etc., are unfeasible. Therefore, a vapor cell with feasible performance parameters plays a significant role in SERFCM;

2) If it is impossible to make these uncontrollable state components controllable by physical means, one can then investigate their stability, and determine whether these uncontrollable components are asymptotically stable or at least bounded-input bounded-state (BIBS) stable, to ensure SERFCM can be normally operational.

VI. CONCLUSION

In this paper, for SERFCM, a nonlinear atomic spin polarization model has been derived from the Bloch equations. In this model, we concern both the variations of transverse as well as longitudinal polarization, and the notion of PSS is introduced according to the real condition. In this case, the model we establish has higher nonlinearity and more difficulty in theoretical analysis, but it is closer to SERFCM in practical engineering with more application value.

For this class of nonlinear systems, we propose and prove a criterion condition of global state controllability, which is the first work to analyze the atomic spin polarization controllability of SERFCM in the related research field. Meanwhile,this criterion condition can also be applied to the controllability analysis for that particular class of nonlinear systems. In addition, we propose a theoretically feasible and reasonable solution of the control input under some physical constraints, which are helpful for the controller design.

We use MATLAB/Simulink simulation software to numerically simulate an K-3He SERFCM model and the simulation results demonstrate the validation of our new controllability determination method.

This paper is the first article of controllability analysis for systems of atomic spin ensembles, whose dynamic behaviors of spin polarization can be described by the Bloch equations.Meanwhile, our conclusions have the potential to be expanded to other systems of precision measuring instruments, which are based on effects of atomic spin and dynamical evolution description by the Bloch equations. Therefore, our theoretical results in this paper are not only pioneering but also of certain universality.

From the aspect of strict theoretical proofs, matrix H indeed vary with the state vectorx. But when concerning the practical SERFCM system normally working at PSS, its control input is usually bounded, and the corresponding variations of the 6 polarization components can be calculated according to the Bloch equations. To evaluate the influence of this control input, we define the relative variational rate of H as below:

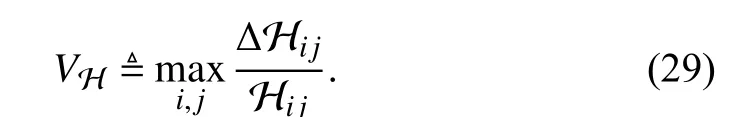
For example, let the control input be a step magnetic field with the amplitude of 1 nT and the corresponding variations of the 6 polarization components have the typical values as in Table II.

TABLE II TYPICAL VALUES OF THE POLARIZATION COMPONENTS AND THEIR VARIATIONS FOR SERFCM BASED ON K-3HE ATOMIC SOURCE AT PSS, UNDER THE CONTROL INPUT OF A STEP MAGNETIC FIELD WITH THE AMPLITUDE OF 1 NT

In this example, the relative variational rateVH=0.0038%≈0, which indicates that the variation of H is very small and can be ignored. One should note that, when SERFCM system is normally working at PSS, the amplitude of the control input is always less than 1 nT, such that theVHinduced by corresponding variations ofx(t) is always less than 0.0038%,and also can be ignored. In this situation, H(x) can be simplified as a constant matrix H in this paper.