基于最小二乘支持向量机的短时交通流预测
桂栋 隗宇 王晓东





摘要 交通流变化过程是一个实时、非线性、高维的随机过程,对其进行准确预测是智能交通领域的热点和难点问题。采用最小二乘支持向量机方法来建立短时交通流预测的模型,在经验风险和置信范围之间寻求最佳折衷,并且通过实例研究来验证其有效性。结果表明,该模型适应小样本情况下对非线性动态系统的学习,对短时交通流有较好的预测效果。
关键词 短时交通流预测;最小二乘支持向量机;结构风险最小化;核函数
中图分类号 U491.1 文献标识码 A 文章编号 2096-8949(2022)07-0047-03
0 引言
短时交通流预测是交通控制与诱导的重要基础,也一直是智能交通研究领域的热点和难点问题[1]。目前,已有许多理论和方法应用于短时交通流预测的研究。基于解析数学的卡尔曼滤波模型、参数回归模型等预测方法,在数理统计回归和时间序列预测的基础上,用解析数学方法来描述状态变量的变化趋势[2],但无法克服随机因素对交通流的干扰;基于知识发现的神经网络、混沌理论等预测方法,更重视对真实交通流现象的拟合效果,但很难建立能适用于所有路段交通流预测的模型[3],且模型参数选择困难,推广与泛化能力不足。
该文以最小二乘支持向量机(Least Squares Support Vector Machines,LSSVM)理论为基础,利用其在小样本学习方面的优势,在结构风险最小化原理基础上 [4],克服过分依赖大样本历史数据的缺陷[5],建立短时交通流预测模型。然后利用来自交通信息采集设备的数据对模型进行训练,并合理确定模型的参数,最终达到预测未来时段短时交通流的目的。
1 最小二乘支持向量机原理
支持向量机借助于最优化方法解决机器学习问题,是数据挖掘中的一项新技术。对于线性回归,用线性回归函数来拟合样本数据;对于非线性回归,通过一个非线性映射,把输入空间的数据映射到一个高维特征空间中去,然后在此空间中做线性回归[6]。
LSSVM是由Suykens[7]等人提出的一种新型的支持向量机方法,采用最小二乘线性系统作为损失函数,利用等式约束来代替标准算法中的不等式约束,将求解二次规划问题转化为求解线性方程式,使得求解难度大为降低[8]。LSSVM在利用结构风险最小化原则时,其优化问题为:
(1)
式中,——误差项;——非线性映射;——惩罚系数。引入拉格朗日函数:
(2)
式中,,——拉格朗日乘子,根据优化条件有:
(3)
可得下式:
(4)
式中,,为核函数。最终,LSSVM的目标函数为:
(5)
由于算法最终转化为矩阵计算,所以LSSVM在计算速度上更具优势。
2 建模与仿真
利用LSSVM算法进行建模,过程如下:
2.1 训练数据的选取与分类
交通流受时间、空间和其他随机因素的影响,变化规律非常复杂,确定影响交通流的因素,对交通流数据进行分类训练,有助于提升模型的预测效果。该文选取上海市南北高架快速路段2020年7月份交通流数据作为训练数据。通过对数据的系统分析,可以发现城市交通流很明显地受天气以及工作日的影响,因此根据影响因素晴天/雨天对交通流数据进行分类训练,建立相应的模型以达到对交通流较为准确的预测。
2.2 核函数的选取
引入核函数可以将高维空间的内积计算转化为简单的函数计算,从而降低计算的复杂度。由于高斯径向基函数在非线性拟合方面具有较好的性能,因此选取高斯径向基函数作为核函数,即:
(6)
2.3 参数的选取
2.3.1 回溯系数的选择
交通流会受到前一个时刻或者多个时刻交通流的影响,故需要在训练过程中选取合适的回溯系数。在选取回溯系数p之前,首先取定LSSVM目标函数中的和核函数中,使预测的结果仅受回溯系数影响。然后利用训练数据和给定的参数来训练LSSVM模型,通过分析对应的误差指标,从而挑选出预测误差最小的回溯系数。
2.3.2 LSSVM参数的选取
选取径向基函数作为核函数以后,需要对LSSVM目标函数中的惩罚系数和核函数系数进行选取。惩罚系数主要影响模型的复杂度和训练误差,核函数系数主要影响模型的学习能力,这两个系数如果选取不合理,则会导致模型出现“欠学习”或“过学习”现象[9]。该文利用训练数据以及2.3.1中选取好的p来训练LSSVM模型,通过误差指标来不断调节和,最终选取合适的参数。
2.4 模型的输入与输出
选取某x日采样周期为10 min的交通流数据作为模型输入1,该输入作为训练数据;选取与x日数据影响因素相同的某y日采样时刻为t的交通流数据作为模型输入2,该输入作为训练后模型的预测输入值;经模型计算后的输出为某y日采样时刻为t+10 min的交通流预测值。
3 实例研究
3.1 误差指标
采用MARE和MAXARE作为误差指标来衡量算法的预测能力:
(1)平均绝对相对误差:
(7)
(2)最大绝对相对误差:
(8)
式中,——实际观测值;——模型预测值。
3.2 仿真预测
采用MATLAB R2007a和Suykens J.A.K開发的LSSVM lab工具箱,根据晴天/雨天对交通流数据进行分类训练,按10 min间隔对交通流进行短时预测。
3.2.1 晴天工作日模型
选取上海南北高架快速路段NBXX05(4车道)2020年7月1日星期五(工作日,晴)7:00—22:50数据为训练数据,来预测2020年7月15日星期五(工作日,晴)7:00—22:50交通流,并计算出误差指标,然后根据误差指标来优化参数。
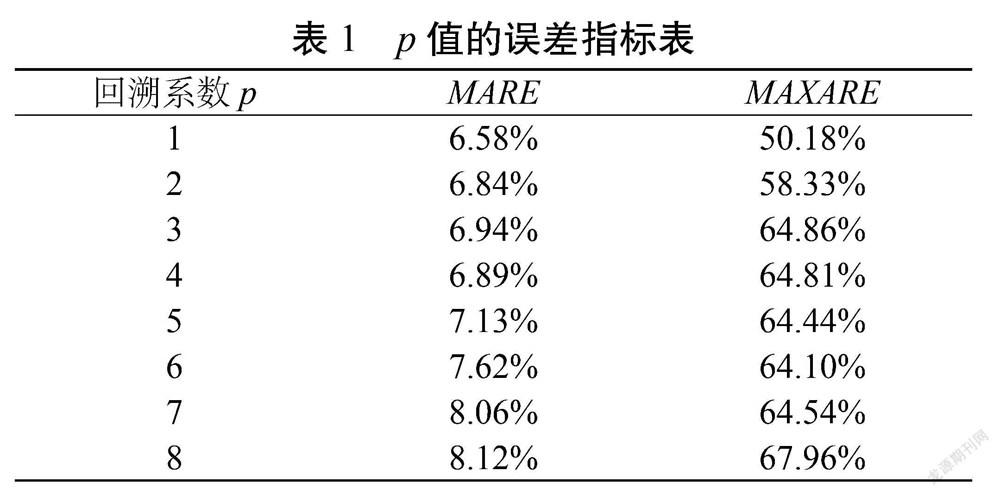
首先通过实验算法初步取定=50,=50来计算相应的p值的误差指标,结果如表1所示。
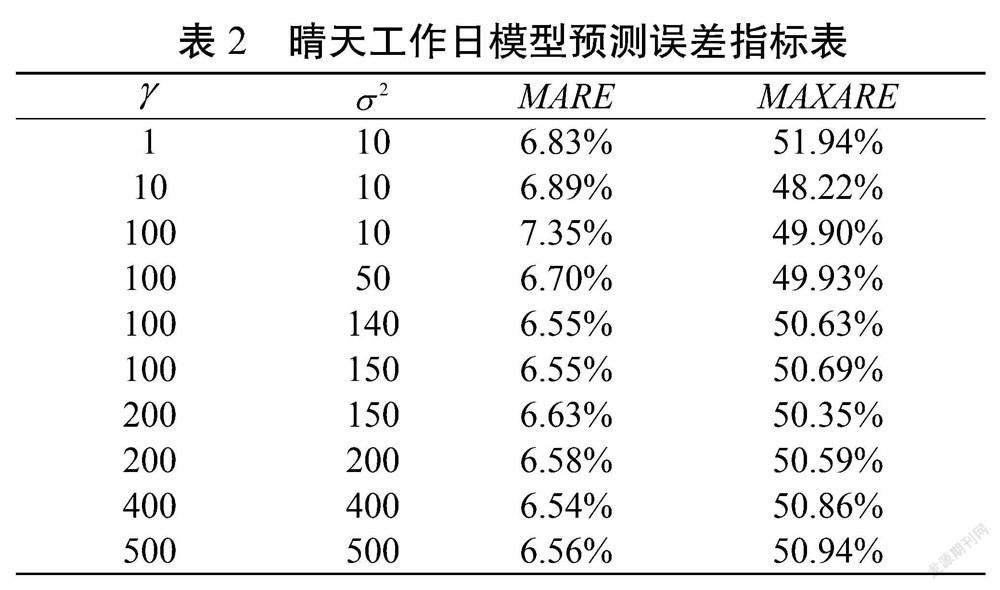
从表1可以看出,当=50,=50时,随着p从1到8逐渐增大,误差值呈现逐渐增大趋势,因而确定回溯系数为1。接下来确定p=1时的最合适的和。采用交叉验证法,根据误差指标的变化趋势来取定和。计算结果如表2。
从表2中可以看到,当=100,=140和=400,=400时,误差指标MARE出现两个局部极小点,但后者更小,此时的平均相对绝对误差为6.54%。相应的实测值与预测值对比如图1。
从图1中的拟合程度看,虽然个别突变点的预测值与实测值相差较大,但模型的预测值符合实测交通流量的整体变化趋势。
3.2.2 雨天工作日模型
选取上海南北高架快速路段NBXX05(4车道)2020年7月7日星期四(工作日,雨)7:00—22:50数据为训练数据,来预测2020年7月14日星期四(工作日,雨)7:00—22:50交通流,计算结果如表3。
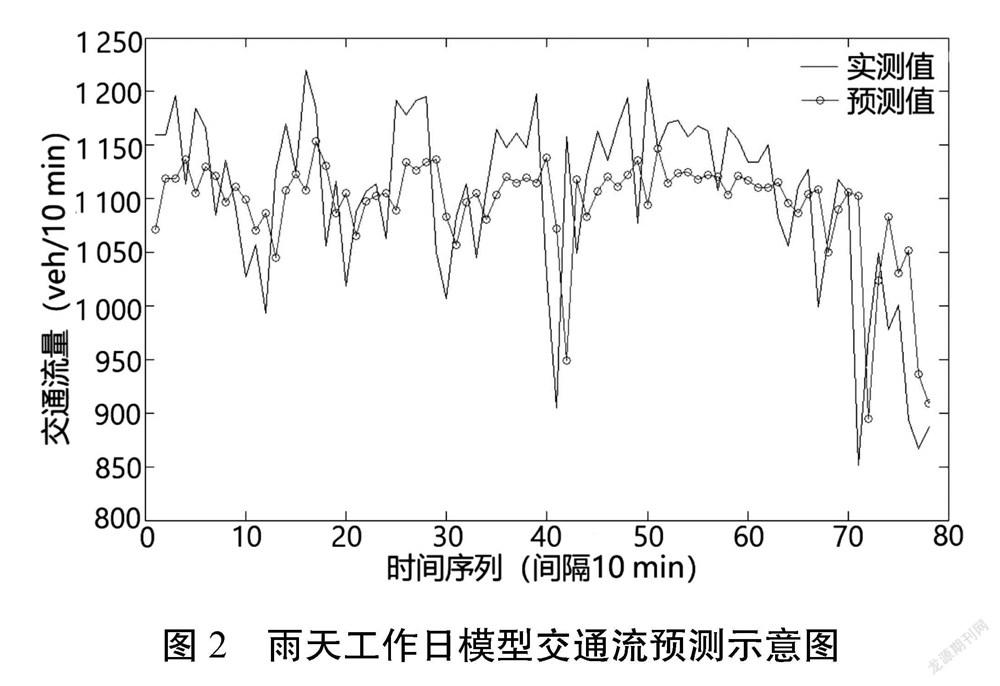
从表3中可以看出,当=80,=10时,误差指标MARE出现极小点,于是取=80,=10,此时的平均相对绝对误差为5.18%。相应的实测值与预测值对比如图2。
3.3 结果分析
经过上节的计算,选出的两种模型参数及预测误差结果如下:
(1)晴天工作日模型:回溯系数p=1,=400,=400。
(2)雨天工作日模型:回溯系数p=1,=80,=10。
在这些参数下,两种模型的最小平均绝对相对误差分别为:6.54%、5.18%,两种模型的预测值均较好地吻合了实测值的整体变化趋势,验证了该预测方法对于t+10 min的短时交通流变化趋势有较好的拟合效果。但在某些变化剧烈的点,预测值与实测值相差明显,这也体现了影响交通流的偶然因素很多,也正是交通流预测的难点所在。
4 结语
该文深入研究总结了LSSVM的原理以及在寻求结构风险最小化、避免“过学习”方面的优势。通过对交通流数据的分类优化,建立基于LSSVM算法的短时交通流预测模型,并通过数据训练确定了模型中的参数,然后利用训练好的模型对短时交通流进行了预测。预测结果表明,基于LSSVM的预测方法适合小样本数据的训练和学习,对短时交通流有较好的预测效果。
参考文献
[1]吴晋武, 张海峰, 冉旭东. 基于数据约减和支持向量机的非参数回归短时交通流预测算法[J].公路交通科技, 2020(7):129-134.
[2]胡洁. 基于混沌和神经网络的短时交通流预测研究[D].武汉:武汉理工大学, 2007: 2-5.
[3]赵亚萍. 基于最小二乘支持向量机的交通流量预测模型[J].北京交通大学学报, 2011(2): 114-117.
[4]罗川. 基于最小二乘支持向量机的短时交通流预测方法研究[D].太原:太原理工大学, 2019: 13-19.
[5]张阳, 杨书敏, 辛东嵘. 改进小波包与长短时记忆组合模型的短时交通流预测 [J].交通运输系统工程与信息, 2020(2): 204-209.
[6]姚智胜. 基于实时数据的道路网短时交通流预测理论与方法研究[D].北京:北京交通大学, 2007: 69-70.
[7]J.A.K. Suykens and J. Vandewalle. Recurrent Least Squares Support Vector Machines[J]. IEEE Transactions On Circuits And Systems—I: Fundamental Theory And Applications, 2000(7): 1109-1114.
[8]姚智勝, 邵春福, 熊志华. 基于小波包和最小二乘支持向量机的短时交通流组合预测方法研究[J].中国管理科学, 2007(1): 64-68.
[9]李巧茹, 郝恩强, 陈亮, 等. 遗传算法优化支持向量机的城市交通状态识别[J].重庆交通大学学报, 2020(8): 1-5.

