基于Shapley-Gray政府公共工程项目投资风险评价

赵 辉， 王 欣

(青岛理工大学 管理工程学院，山东 青岛，266520)

我国在加速城市化发展的过程中，采取了积极的财政政策，建设了大量的固定资产，极大地促进了区域经济的快速发展.其中，政府公共工程项目作为社会固定资产投资的重要组成部分，集政治、文化、经济导向于一身，是项目所在地向广大人民群众展现文化底蕴、历史情感、经济实力的有效窗口.它能够从侧面反映出该地区的政治、经济、人文、社会、资源等各方面的发展状况.但由于政府在投资过程中受信息不对称等资源配置问题的影响，政府投资项目决策频频失误，投资决策的科学性受到各界人士以及广大人民群众的关注和质疑.造成政府公共工程项目投资决策失误的主要原因之一就是当前政府投资决策体系尚不完善，对其投资风险没有进行合理的评估.

当前，专门针对政府公共工程项目投资风险评价的研究较少，但其他各类项目投资风险方面的研究众多，为本文后续研究奠定了良好的理论基础.如马力等[1]和袁宏川等[2-3]均通过云模型分别对政府公共工程项目、污水处理PPP项目和水利PPP项目进行投资风险评价；毛亮等[4]和周启清等[5]均采用模糊综合评价法分别对PPP项目和房地产项目进行投资风险决策分析；唐碧秋等[6]采用粒子群算法改进的支持向量机构建了工程项目的投资风险评估模型；郭莹[7]则重点关注中国海外基建项目，采用未确知测度模型进行投资风险评价.从已有研究成果来看，投资风险评价方法在进行指标权重确定时大都习惯采用主观赋权方法，主观性太强，容易造成评估结果与真实情况的偏差；在评价模型的选择上也大都未考虑指标的灰度.因此，本文将Shapley值与灰色聚类评价相结合构建基于Shapley-Gray模型的综合评价方法对政府公共工程项目进行定量评价，通过Shapley值来消除指标间存在的共性关系，使得灰色聚类来评估数据时得到的结论更加科学、合理.

1 政府公共工程项目投资风险指标体系的构建

目前政府公共工程项目尚未形成一套完整全面的投资风险指标体系，为此本文主要参考了《政府投资项目经济评价方法与参数研究》和《建设项目经济评价方法与参数》(第3版)[8]中对政府投资项目评价的相关属性，并归纳整理了相关文献中给出的风险指标，如马力等[2]从经济、社会、环境以及质量和技术四个方面构建了指标体系；刘伟军等[9]从政策、经济、项目建设、自然等多个方面分析了投资风险要素等；程鸿群等[10]从宏观环境、政府、项目公司、承包商、供应商、设计方和监理方七个方面构建了城市公共基础设施项目投资风险评估指标体系；赵成[11]从可持续建设的角度将公租房项目的投资风险划分为建设期、出租期和租售期三个阶段，并综合考虑了经济、质量、法律、政策等多方面风险因素；袁家凤等[12]将公路投资风险划分为内部风险和外部风险，内部风险包括建设、技术和管理风险，外部风险包括政策、金融、市场和不可抗力风险.综合上述文献材料，本文主要从经济、政策、社会、建设、自然、环保和法律七个方面归纳总结和构建了政府投资工程项目投资风险指标体系，如图1所示.

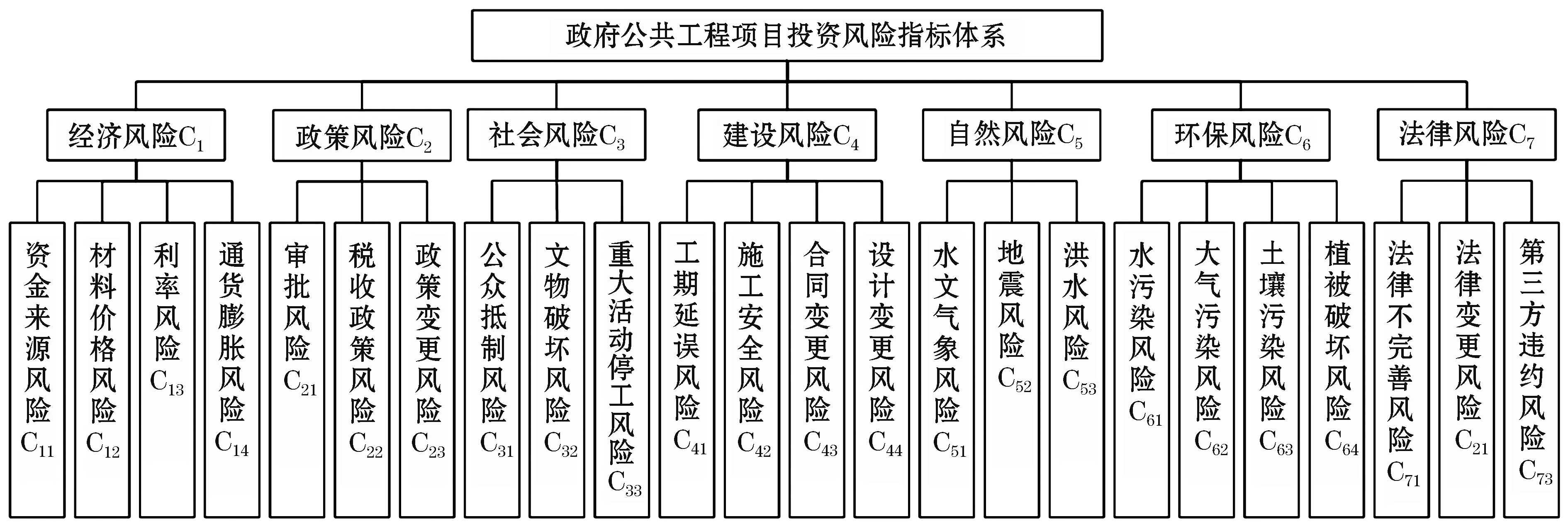
图1 政府公共工程项目投资风险指标体系

2 基于Shapley-Gray模型的投资风险评价方法

以政府公共工程项目为研究对象，基于Shapley-Gray模型对其展开投资风险评价.由于政府公共工程项目涉及到经济、社会、环境等各方面问题，因此需要考虑的风险要素众多，而这些风险要素之间必然存在着一定的线性关系.首先借助Shapley值赋权方法来确定风险指标的权重；然后采用Gray模型，通过白化权函数来对具体的项目展开评价；最后计算得到评价数值，从而确定当前的决策风险状况.

2.1 Shapley值赋权方法的设计

大多学者在进行投资风险评价时，往往采用传统的主观赋权方法，即使是应用了熵权法等进行客观权重的计算，也均是在可加测度下进行的.但实际上，指标之间都存在着一定的线性关系，两个或多个指标的权重影响程度不能通过简单的加法来实现，而是应当考虑它们之间的相互作用关系，在非可加测度下实现权重的计算[13].Shapley值[14]是数学家L·S·Shapley于1983年提出，通过强调个体与整体之间存在相互关联性来解决多个合作方之间的利益分配问题，是一种有效解决指标间共性问题的一种非可加测度赋权的方法.以 Shapley值赋权方法对政府公共工程项目投资风险进行权重计算，使赋权结果更加合理、科学，符合实际情况.具体步骤如下：

1)对决策数据(a1,a2,…ai,…an)进行无量纲化处理，确定各指标影响值：

(1)

2)计算各指标组合的影响值，根据Shapley值数学理念，若两个指标之间存在线性关系，两者的组合影响值不是两者影响值的简单相加，而应当小于两者影响值之和，为此通过赋予两者之和一个系数0.7来实现线性关系下的指标组合影响值计算；若两个指标之间不存在相互关系，而是独立存在的时候，两者的组合影响值应当大于两者影响值之和，为此通过赋予两者之和一个系数1.3来实现两两独立下的指标组合影响值计算；若两个及以上的指标进行组合，则以多数指标是否具备线性关系为判断依据，从而进一步再确定系数的大小，指标组合影响值的计算公式如下：

(2)

3)计算各指标Shapley值，即确定各指标权重大小

ωi=shi(N,V)=

(i=1,2,3,…,n)

(3)

2.2 基于Gray模型的风险评价步骤

2.2.1 投资风险测度的确定

在进行政府公共工程项目投资风险评价时，最终的结果是具体的数值，这个数值则是对于风险的量化值，而对于风险大小的测度需要进一步进行合理的界定，风险等级和数值测度之间的对应关系如表1所示[15].

表1 投资风险等级测度

2.2.2 白化权函数的建立与评价灰类的确定

灰色系统理论将某个灰类最大程度的点表示为该灰类的中心点，通过中心点向量原则，由表1确定的“低、较低、中等、较高、高”五个灰类确定中心点为U=(9，7，5，3，1)，通过中心点三角白化权函数模型来描述灰类所属情况[16-17]，如表2所示.

表2 白化权函数表

2.2.3 计算步骤

在确定灰类、灰数(政府公共工程项目投资风险指标体系具有灰色系统的特征，可以确定为一个灰色系统)及相应的白化权函数后，对投资风险指标体系进行灰色聚类评估，步骤如下：

1)建立评价矩阵.邀请p个专家对指标进行赋值Cij，建立评价矩阵Di=[dijk]s×p,其中dijk为第k个专家对第i个指标的第j个下属指标的赋值(k=1,2,…,p)，该评价矩阵指标数量用s表示.

2)构建灰色聚类权矩阵.

(4)

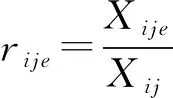
3)确定聚类评价矩阵.将求得的评价矩阵与灰色聚类权向量进行矩阵运算，对各一级指标进行聚类评价：

ZI=ωi·Ri

(5)

基于式(5)的结果构造一级指标综合评价矩阵Z0=[Z1,Z2,…,Zn]T，由下列公式得到最终的政府公共工程项目投资风险风险综合聚类评价向量：

M=ω0·Z0=[M1,M2,…,Mn]

(6)

4)计算综合评价值.由综合评价向量M与灰色测度阈值U相乘，得到单值化的综合评价值，能够避免以最大权原则确定灰类时可能会发生的信息缺失问题，在一定程度上能够降低评价结果的偏差：

W=M·U

(7)

3 实证分析

某市拟新建一个文体公园-图书馆一体工程项目，建设总占地面积约48 000 m2，同时建设供水电、照明、消防、道路、绿化景观等配套设施.建设资金来自于政府拨款，项目预算总投资10 000万元.应用前文所建立的Shapley-Gray模型对该政府公共工程项目进行投资风险分析和评价.现邀请对该项目有深入了解的3名资深专家、2名政府工作人员和2名咨询单位从业人员组成专家小组，对该项目的投资风险进行评价.

首先，以经济风险下的四项指标为例，7名专家分别对四项指标的重要程度进行打分.采用0～10打分法时要求打分数据均为0.5的倍数以方便数据处理，分值越高说明该指标的重要性越高，通过专家打分获取投资风险评价指标初始打分表(如表3所示).

表3 投资风险评价指标打分表

其中：指标C13与C14关联性较强，根据式(1)、(2)计算各指标评价值v(n)与组合评价值v(1,2,…,n)，结果如下：v(1)=0.250，v(2)=0.246，v(3)=0.248，v(4)=0.256，v(1,2)=0.595，v(1,3)=0.598，v(1,4)=0.607，v(2,3)=0.593，v(2,4)=0.602，v(3,4)=0.403，v(1,2,3)=0.893，v(1,2,4)=0.902，v(1,3,4)=0.603，v(2,3,4)=0.600，v(1,2,3,4)=1.

根据式(3)计算各指标Shapley值，求得C11=0.344，C12=0.304，C13=0.172，C14=0.180.则C1的权重向量为：wc1=w1=(0.344,0.304,0.172,0.180).

同理计算C2～C7权重向量，结果如下：

w2=(0.330,0.323,0.347) ；

w3=(0.352,0.347,0.301) ；

w4=(0.242,0.344,0.209,0.205) ；

w5=(0.388,0.341,0.271) ；

w6=(0.299,0.280,0.228,0.183) ；

w7=(0.342,0.353,0.305) ；

一级指标的权重：

w0=(0.138,0.141,0.145,0.148,0.149,0.147,0.132) .

7名专家对照投资风险等级测度表(表1)为打分标准对风险指标打分，由此构建决策矩阵Di=[dijk]s×p如下：

根据表2中的白化权函数以及公式(4)计算聚类权矩阵Ri:

根据公式(5)得到综合评价矩阵Z0:

根据式(6)得到综合评价向量M：

M=ω0·Z0=[0.324, 0.366, 0.278, 0.032, 0.000]

根据式(7)得到单值化处理后的投资风险综合评价值W=M·U=6.906.对指标C1～C7做单值化处理，计算每个一级指标的评价值：W1=6.866，W2=7.152，W3=7.071，W4=6.761，W5=6.821，W6=6.642，W7=7.141.对照表1中的风险测度和风险值的转化关系可知，该项目整体投资风险值为6.906，对应的风险大小为“较低”.从得到的各项一级指标的风险值来看，各项一级指标的风险大小均为“较低”，可见该项目投资效益良好.

4 结 语

政府公共工程项目作为社会固定资产投资的重要组成部分，在进行投资之间先对可能出现的投资风险进行量化评估将有助于提升政府投资决策水平，减少决策失误.为此，提出了一种基于Shapley-Gray模型的政府公共工程项目投资风险评价方法，对完善政府投资决策体系有一定的参考价值.该方法集结了Shapley值客观赋权的优势以及Gray模型处理模糊信息的能力，能够在项目投资前有针对性的进行风险评价，预先得到相应的风险大小，政府可以据此来采取针对性措施降低投资风险，从而提升决策水平，提高项目投资效益.