基于结构的加权对齐计算方法

魏 瑶，邵叱风*,2

(1.安徽理工大学 数学与大数据学院， 淮南 232001；2.安徽科技学院 信息与网络工程学院， 蚌埠 233100)

信息系统越来越多地用于实现和支持业务流程.流程挖掘[1]是一种从企业信息系统生成的事件日志等数据中发现流程模型的技术，它可以指导业务经理更准确，更直观地了解其业务流程[2].事件日志与流程模型的对齐对于流程挖掘以实现一致性检查，流程增强，性能分析和迹修复非常重要[3].一致性检查[4]旨在评估事件日志中记录的过程模型和事件数据是否彼此一致.近年来，对齐已被证明对于计算一致性统计数据极为有用.由于过程模型变得越来越复杂，并且事件日志可能会通过显示冗余，丢失和错位的事件而偏离过程模型，因此确定日志中每个事件序列的最佳对齐是一项挑战[5].

现有的方法利用基于成本的算法来解决这个问题.但是，通常不考虑活动之间结构关系，这在进行对齐计算时会影响最优对齐的结果.Petri网是一种具有优秀系统模拟能力的建模语言[6].文献[7]基于Petri网正式定义了业务流程中的一些异常活动,提出了一种有效的方法来检测过程模型和事件日志之间的偏差,在存在异常活动时修订业务流程模型.文献[8]提出了一种新的基于Petri网模型和迹的对齐方法来提高对齐效率，该方法可以基于标准似然成本函数生成包括给定迹和Petri网模型之间的所有最佳对齐的最佳对齐树.文献[9]提出了一种基于逻辑Petri网的新模型修复方法，该方法可以在原始模型上选择分支添加新的活动.文献[10]提出了一种基于逻辑Petri网对具有不完全选择和并发结构的过程模型修复方法，通过分析最佳对齐方式中的关系集和活动之间的关系来确定偏差，根据不同的偏差位置通过逻辑Petri网提出了模型修复方法.

可以说, 日志与给定模型的对齐已经成为了一种新的研究趋势.在对齐计算时,经常出现对齐偏差不同，需要根据成本的算法来进行最优对齐的选择[11-13].现有的对齐方法仅依据日志与给定模型的移动个数，而忽略活动之间的结构关系[14-15].针对这个问题，本文基于活动的结构进行加权对齐成本的计算.

1 基本概念

Petri网广泛应用于并行系统的仿真和分析,基于其坚实的数学定义和图形表达式，它可以有效地描述和分析并发、异步、分布式、并行和不确定的信息系统.因此，本文采用Petri网来描述过程模型.

图1 标签{a,b,c,d,e}分别代表原先网N1中对应变迁的标签

如果λ(t)≠τ，t∈T，那么t是可观测的，反之t是静默变迁.标签的执行语义是根据状态和状态转换定义的.标签网的状态由标识的概念俘获.

定义2 (基本结构)过程模型包含三种基本结构，它们是顺序、选择和并发.序列意味着两个变迁直接通过一个库所连接，见图2(A)，这表示这两个任务之间的因果关系.一个选择包含一个具有一个输入变迁和两个或多个输出变迁的库所，见图2(B)，或者一个或多个输入变迁和一个输出变迁，见图2(C).并发结构的特殊之处是具有两个或多个输出库所(图2(D))或输入库所(图2(E))的任务.

图2 基本结构:(A)顺序;(B)和(C)选择，(D)和(E)并发

Move(x,y)是一个日志迹上的移动，当且仅当x∈A且y=→.

Move(x,y)是一个系统上的移动，当且仅当x=→且y∈T.

Move(x,y)是一个同步移动，当且仅当x∈A,y∈T,且λ(y)=x.

(1)

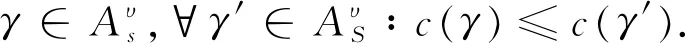
即日志迹υ与模型中可观测迹的对齐成本最小的对齐为最优对齐，可能有多个最优对齐.比如两个对齐均插入或跳过一个活动，为体现日志与网系统中变迁的重要程度，降低最优对齐个数.下面给出定义7和定义8移动加权如下：

定义7 (标签加权)依据活动不同重要性，考虑单一活动成本，对对齐序列中的标签γi进行加权处理，对于权函数w，w(π1(γi)|A)=w(π2(γi)|T)=ω(γi).

定义8 (移动加权)依据偏差出现位置，考虑其对对齐成本的影响，在计算总的对齐成本时对于系统上的合法移动，迹上的合法移动按类别WeightSkip、WeightInsert进行加权处理.输入形式如

WeightSkip/WeightInsert∶(Costskip,

W(Costskip),Costinsert,W(Costinsert)).

CostTotal=Costskip*W(Costskip)+

Costinsert*W(Costinsert)

(2)

则c(γi)=

(3)

定义9 (最优对齐成本)事件日志L∈B(A*)与网系统S∈S的最优对齐成本根据在S上的合法移动的成本函数c及加权函数w，定义为

(4)

通过对活动的加权，区分了对齐中不同活动的成本；对偏差类别的加权，区分了偏差发生位置的重要程度；相较于单一量化偏差个数的对齐成本求解进行了改进.

2 基于结构的对齐成本加权计算

2.1 结构加权定义的提出

现有的对齐方法仅有活动个数，忽略活动之间的结构关系，如图3中b、c间为并发关系，在日志中表现为<…,b,c,…>或<…,c,b,…>,则会出现对齐结果如abc→defhi‖a→cbdefhi，对齐成本为2，实则交替活动b,c发生次序并不应影响最优对齐结果，此时应弱化b,c在对齐计算中的权重；如图3中d,e间顺序关系，d,e必在一条日志迹中依次出现，如果出现<…,d,…>或<…,e,…>,此次对齐必存在活动缺失问题，此时应提升d,e在对齐计算中的权重；如图3中f,g之间的选择关系，f,g在一条日志迹中仅可出现其中一个，如出现<…,f,g,…>或<…,g,f,…>,此次对齐必存在活动执行问题，此时应提升f,g,在对齐计算中的权重.现依据活动之间结构关系，对标签进行加权，提出定义10，定义11.

●选择结构：对于变迁ti,tj有.ti=.tj={si}，则称ti,tj为选择关系，w(ti,tj)=1；

●并发结构：对于变迁ti,tj有.ti={si}，.tj={sj}，且.si=.sj={tk}，则称ti,tj为并发关系，w(ti)=1/|tk.|；

定义11 (全局权重)对于标签权重

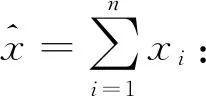
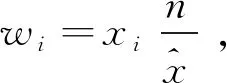
2.2 权重自动化计算方法

依据定义10结构关系权重，提出一种自动化获取活动结构权重的方法，如Code_1所示.基于这种方法，再对得到的活动权重进行归一化计算，获取活动全局权重，如Code_2所示；

Code_1结构权重获取

01PetriNet N;

02T={a,b,c,d,e,...,i};

03Wt={(a,wa),(b,wb),...,(i,wi)};

04While(T.size() > 1){

05 for earch t in T{ //移除非直接关联的选择及并发

06 if((ti,tj)is Order){

07 w(tj)=1;

08 Wt.put(tj,w(tj))；

09 N.remove(tj);

10 }

11 }

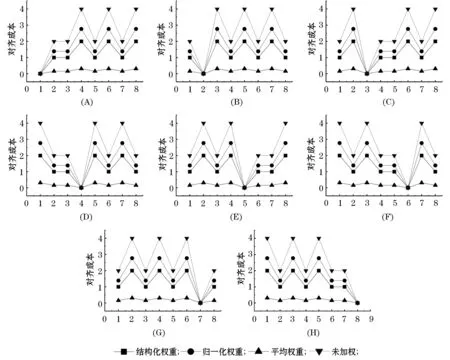
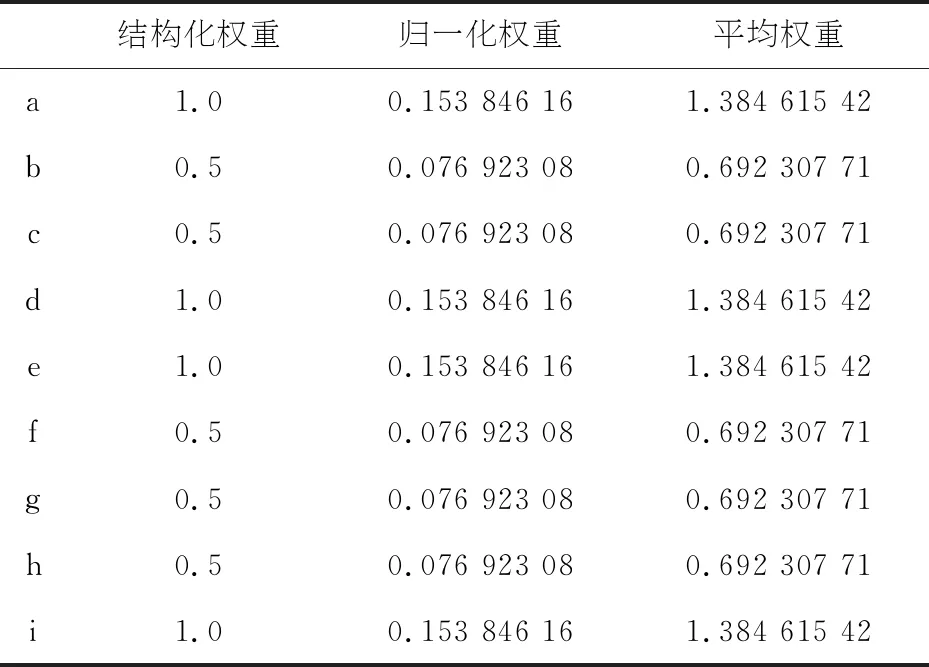
12 for(i=1,i++,i

13 for(j=1,j++,j<=T.size()){

14 if((ti,tj)is Choice && tj not in Wt)

15 w(tj)=1;

16 Wt.put(tj,w(tj))；

17 N.remove(tj);

18 }

19 w(ti)=1;

20 }

21 for(i=1,i++,i

22 for(j=1,j++,j<=T.size()){

23 if((ti,tj)is Concurrent && tj not in Wt){

24 map.put((i,j),C);

25 }

26 }

27 X={ti}∪tj in map；

28 for each x in X{

29 W(x)=1/(map.size()+1)；

30 Wt.put(x,w(x))；

31 if(x is not ti){

32 N.remove(x);

33 }

34 }

35 }

36}

在Code_1中，利用While循环，首先移除非直接关联的选择及并发，再对选择结构进行加权，并发结构进行加权，直至N中的变迁数量为1；Code_1(5～11),对活动进行遍历，若存在顺序结构，移除跟踪活动，并标记其结构权重为1；Code_1(12～20),对活动进行遍历，若存在选择结构，且备选活动未加权，标记备选活动其权重为1 ，并移除备选活动，最后标记主选择活动权重为1；Code_1(21～35),对活动进行遍历，将存在并发关系且未加权活动放入map,利用Code_1(27～34)对map中活动进行加权处理.

Code_2归一化权重计算方法：

01 public static void main(String[] args) {

02 String str = "a,1,b,0.5,c,0.5,d,1,e,1,f,0.5,g,0.5,h,0.5,i,1";

03 String[] labelWeight=str.split(",");

04 DecimalFormat dF = new DecimalFormat("0.00000000");

05 float fenmu=0;

06 for (int i = 1; i < labelWeight.length; i=i+2) {

07 fenmu=fenmu+Float.parseFloat(labelWeight[i]);

08 }

09 for (int i = 0; i < labelWeight.length; i=i+2) {

10 System.out.println(labelWeight[i]+":"

11 +dF.format(((float)Float.parseFloat(labelWeight[i+1])*(labelWeight.length/2)/fenmu)));

12 }

13}

在Code_2中，对于已有的活动权重进行归一化计算，如定义11所示，Code_2(6～8)首先计算， Code_2(9～12)分别输出的值.对于图1模型有如图4所示的算法执行过程：

图4 权重自动化计算执行过程

3 实验与分析

本节利用实验来评价基于结构的对齐成本加权计算方法，并将结果与传统对齐方法得到的数据进行了比较.

3.1 实验设置

本文利用一个包含顺序、选择及并发结构的模型及其部分系统日志，对该方法的可行性及有效性进行了验证.

实验选取的模型所有完整可执行路径为Traces={,,,,,,,}.

首先，将所有路径之间进行相互对齐，对齐结果如表1所示，然后根据上述算法，分别计算出结构化权重，归一化权重和平均权重，结果如表2所示，图5为得到的结果与传统对齐方法得到的数据之间的对比.

图5 Traces与Traces对齐计算成本对比

表1 Traces与Traces对齐计算结果

表2 权重计算结果

3.2 实验结果分析

实验结果表明，加权计算对齐成本的方法是可行的，且最优对齐的计算方法在一定程度上体现了不同活动的重要性，增加了最优对齐对活动的依赖性，降低了日志迹与模型之间相同最优对齐成本的个数.

4 结 语

本文阐述了流程挖掘在企业信息系统中重要的位置，其中事件日志与流程模型的对齐对于流程挖掘以实现计算一致性统计数据具有极大的推动作用.引出对于对齐中存在的活动权重无差别的问题，提出了加权对齐的观点，并基于模型结构提出了最优对齐加权计算方法，该方法考虑到在模型中活动之间的结构关系会影响到对齐的精准度，因此可以基于模型的结构而对活动进行加权，从而得到加权后的对齐成本.实验表明，通过这种方法，可以改进之前的成本计算方法，确定最优对齐，高效而准确地进行一致性检查.

在未来的工作中，将在求解所有对齐、排序最优对齐时加入多线程的使用来提高计算效率，并且对于加权计算后得到的不同对齐成本，进一步分析其对一致性检验的影响.