循环MDS矩阵的构造

孙春雨， 陈博聪

(华南理工大学 数学学院， 广东 广州 510641)

循环MDS矩阵不仅在编码理论中很重要， 而且在密码学中也有许多应用. 本文在文献[1-3]的基础上， 提出了有限域上循环MDS矩阵的新构造， 并构造了奇特性有限域上的一类循环对合MDS矩阵.

1 准备知识

令Fq为具有q个元素的有限域，n表示一个正整数. 令Fq[X]为变量X的多项式环， 其系数在Fq中， 并令

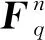
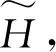
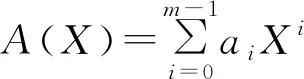
(1.1)

被称为与多项式A(X)相关的循环矩阵. 然后， 可以通过将A到A(X)来验证Fq上的m×m循环矩阵的环与商环Fq[X]/〈Xm-1〉同构.

最后， 我们需要从文献[5]和文献[6]得到一些关于Fq上长度为2m的2-准循环码的已知结果. 注意文献[5]和文献[6]已经发展了关于在Fq上长度为lm的2-准循环码的一般理论; 然而， 出于我们的使用目的， 我们只重申在特定情况下l=2时的结果.

Fq[X]/〈Xm-1〉×Fq[X]/〈Xm-1〉的Fq[X]/〈Xm-1〉子模称为在Fq上长度为2m的2-准循环码. Lally和Fitzpatrick[5]表明，Fq上长度为2m的任何准循环码都具有关于上的POT项序以减少的Gröbner基形式存在的生成集. 这个基可以用上三角2×2矩阵的形式表示如下:

(1.2)

其中元素在Fq[X]中， 必须满足以下条件:

(1) degg1， 1(X)>degg0， 1(X);

(2)g0， 0(X) 和g1， 1(X)是Xm-1的除数;

(3) 若g0， 0(X)=Xm-1， 则g0， 1(X)=0.

Semenov和Trifonov[6]提供了一种有效的方法， 一旦获得了C的具有简化的Gröbner基形式(1.2)的生成矩阵， 就可以找到C的奇偶校验矩阵.

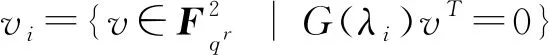
是通过堆叠向量vij获得的ui×2矩阵. 构造一个ui×2m矩阵

(1.3)

假设λ0，λ1， …，λt-1都是C的不同特征值， 并且λi在0≤i≤t-1时具有多重ui. 因此， 我们有t个矩阵H0，H1， …，Ht-1. 从文献[6]引理2得出:

(1.4)

是一个(2m-k)×2m矩阵， 其秩等于2m-k， 其中k是C的维数. Semenov和Trifonov[6]进一步得出结论，H可以用作C的奇偶校验样矩阵， 如下所示.

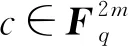
2 主要结论

令C为Fq上的[2m，m]-线性码， 具有生成矩阵

G=(Im∣A)，

其中Im是m×m单位矩阵，A是m×m循环矩阵， 如(1.1)所示. 在本节中， 假设m与q互素. 我们的最终目的是明确找到0≤i≤m-1的Fq的m值ai， 使得C是MDS码.为此， 我们要给出C的一个奇偶校验矩阵.为此， 我们首先证明C可以看作Fq上长度为2m的2-准循环码. 由于G=(Im|A)是C的生成矩阵， 因此可以得出

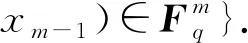
然后， 我们有以下引理.

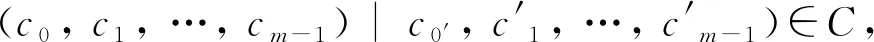
我们有

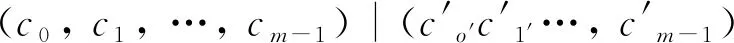
=(c0，c1， …，cm-1)(Im∣A).

对于所有0≤i≤m-1

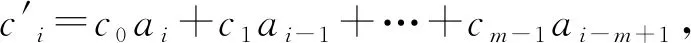
其中a的下标以模m计算.容易验证:

=(cm-1，c0， …，cm-2)(Im∣A).

我们注意到， 具有引理1.1的双循环性的码在文献中称为双循环码(例如参见[7]). 如[7]所述， 将

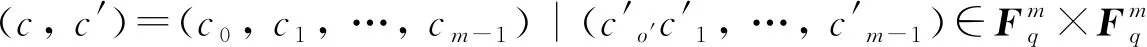
映射到

∈Fq[X]/〈Xm-1〉×Fq[X]/〈xm-1〉

的映射为

的双射. 显然，

Fq[X]/〈Xm-1〉×Fq[X]/〈Xm-1〉在通常意义上是Fq[X]/〈Xm-1〉模; 此外， 标量乘法X对应于向量(c，c′)的双循环移位. 因此，C可以视为

Fq[X]/〈Xm-1〉×Fq[X]/〈Xm-1〉

的Fq[X]/〈Xm-1〉子模. 换句话说，C是在Fq上长度为2m的2-准循环码(例如参见[6]或[7]).

接下来， 我们的目标是通过使用文献[6]中介绍的方法为C导出一个奇偶校验矩阵. 现在很容易看出，C是由(1，A(X))生成的， 其中

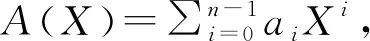
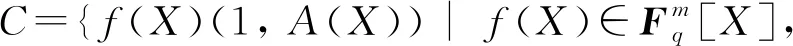
degf(x)≤m-1}

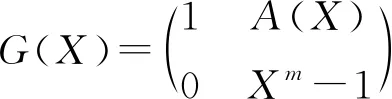
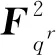
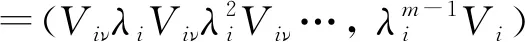
=(αi， 1λiαiλi，λ2iαi，λ2i， …，λ(m-1)t)

此时我们得到形式为(1.4)的C的奇偶校验矩阵:

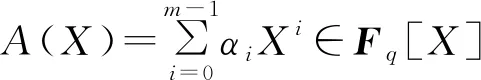
其中δ=λ-1也是Fqr中第m个单位根.

定理2.1假设m>1是q-1的除数.令

λ∈Fq为本原的第m个单位根. 令α≠1是Fq的一个非零元素， 以使Fq的乘法群中α与m互素. 令

相反， 假设对于某个0≤i，j≤m-1有λi=αλj， 得出α=λi-j. 假设Fq的乘群中的α的阶等于s. 因此， 1=αs=λs(i-j).然后， 我们看到m是s(i-j)的因子. 由假设s与m互素， 则m是i-j的因子.推出i=j， 因此α=1. 这与α≠1矛盾.

推论2.1令q为奇素数， 令Fq中α=1. 假设m>1是q-1的奇因子. 令λ∈Fq是本原的第m个单位根. 设δ=λ-1且

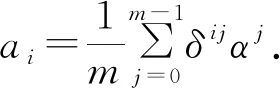
相关的循环矩阵是循环对合MDS矩阵.