电源固定板的振动疲劳分析及试验研究
王 志,丰霞瑶,李志强
(中节能晶和科技有限公司,江西南昌 330029)
0 引言
近年来,各行各业越来越注重产品的疲劳强度问题。疲劳失效分析涉及多项领域,如汽车、航天航空、航海、能源、国防、铁路、海洋工程及一般的机械制造等工业领域。引起疲劳失效的原因主要是结构承受扰动载荷,在经历足够多的循环作用后产生裂纹,裂纹扩展最终导致机体结构破坏。振动就是一种典型的扰动载荷形式。为此,人们针对产品使用工况进行一系列的振动试验,检测产品是否发生疲劳失效。
姚起杭等[1]阐明了结构振动疲劳问题的概念和定义,用两者的不同特点区分了其与常规结构疲劳,把疲劳规整为结构静疲劳和动疲劳。马一江等[2]基于Paris公式和传递矩阵以无质量弯曲弹簧等效裂纹,提出一种可求解含多条裂纹梁疲劳寿命的预估方法。结果表明,裂纹数量、裂纹位置和深度对梁的模态参数和疲劳寿命有重要影响。潘利科等[3]以整体吊弦为研究对象,对比国内外检验方法提出了一种新的模拟其服役过程的等效振动疲劳试验方法,并根据此方法设计了两种不同结构的整体吊弦振动疲劳试验设备。
在城市照明的灯具行业,由于灯具应用场所广泛,如道路、桥梁、天桥和隧道等,这些工作环境不可避免地存在振动,有可能引起灯具共振而产生疲劳破坏。因此,本文针对本公司的一款隧道灯,采用有限元仿真技术借助HyperWorks平台进行振动疲劳仿真,并用振动试验加以验证,为日后公司利用仿真指导结构设计优化提供支撑。
1 疲劳分析方法
目前,疲劳寿命预测具有三种经典方法,分别是S-N(总寿命法)、E-N(裂纹起始寿命法)和LEFM(裂纹扩展寿命法)。这几种方法都依赖于相似性,第一种是名义应力或弹性应力和总寿命之间的关系,第二种是局部应变和裂纹起始寿命之间的关系,第三种是应力强度因子和裂纹扩展速率之间的关系。
本文利用S-N名义应力法进行分析,结合Miner线性损伤累计得到受到不同应力、应变幅值的总损伤和总寿命。HyperWorks中的OptiStruct求解器能专业地进行5~30Hz区间的扫频振动疲劳计算。
在分析过程中,有限元软件需要用户定义模型中不同零件相对应的材料和扫频振动特性参数等。LCF和HCF分别表示低周疲劳和高周疲劳,Fatigue Limit为疲劳极限。
在OptiStruct求解器中,对于钢材材料默认定义式为:

式中:UTS—材料极限抗拉强度。
Miner线性损伤累计依次计算某应力幅值下单次循环损伤的表达式:

n次循环损伤:

不同应力、应变幅值总损伤:

由此得到总寿命:

2 有限元分析
将隧道灯3D模型导入到HyperMesh中进行网格划分,网格总数204496个。
本文主要通过分析电源固定板的振动疲劳情况来反映有限元分析的有效性,并指导优化设计,在1mm厚的电源固定板出现疲劳破坏后将其厚度优化至1.5mm,以下将优化前后的有限元分析情况进行统一介绍。电源固定板的网格数均为176个,单元类型为PSHELL。除灯壳材料为ADC12,单元类型为PSOLID外,其它零件材质为SPCC,单元类型为PSHELL,阻尼取经验值0.04。
2.1 静力分析
在隧道灯网格模型上各零件间建立相应连接关系,然后对其U型支架固定点施加全约束,考虑自身重力进行静力分析。
结果表明电源固定板在固定位置附近所受应力最大。也就是说固定位置附近是该零件的危险部位,经过载荷循环加载有可能发生疲劳断裂。
2.2 频响分析
隧道灯在振动试验时,振动台通过程序控制端对其施加沿z方向3g正弦扫频振动,扫频区间为5~30Hz。由于低频段加载时位移会放大,为了避免试验时结构破坏,在5~19.2Hz低频段进行4mm位移控制。
在U型支架固定点设置单位加速度载荷,完成在OptiStruct求解器中对动态载荷RLOAD2的定义:

式中:A—单位加速度;B(f)—激振对数型目标谱。因无时间延迟,默认φ(f)+θ-2πfτ=0。根据分析计算需求,可以综合使用频率设置FREQi卡片来有效捕捉载荷拐点或者共振峰值。
结果表明,电源固定板在激振频率为9.57Hz时达到共振点,1mm电源固定板所受应力最大,应力值为157.7MPa,小于材料的屈服极限;此时1.5mm电源固定板所受最大应力为45.2MPa,远小于材料的屈服极限。
2.3 疲劳分析
依据疲劳产生机理,虽然共振状态下的名义应力值并未超过材料的屈服强度,在本模型的扫频振动循环作用下,循环次数为110次。电源固定板依然可能由于载荷的反复变化引起疲劳损伤继而产生断裂失效。
在OptiStruct求解器中设置疲劳分析流程管理器,创建疲劳工况,选择SN扫频疲劳选项,定义疲劳分析参数。然后定义疲劳单元和材料,利用材料的抗拉极限生成SN曲线。接着导入频响分析结果,定义好各流程参数后提交疲劳作业。
将运行后的结果用HyperView查看,损伤结果见图1。图中1mm电源固定板除蓝色区域可能产生疲劳断裂;1.5mm电源固定板则无疲劳损伤。
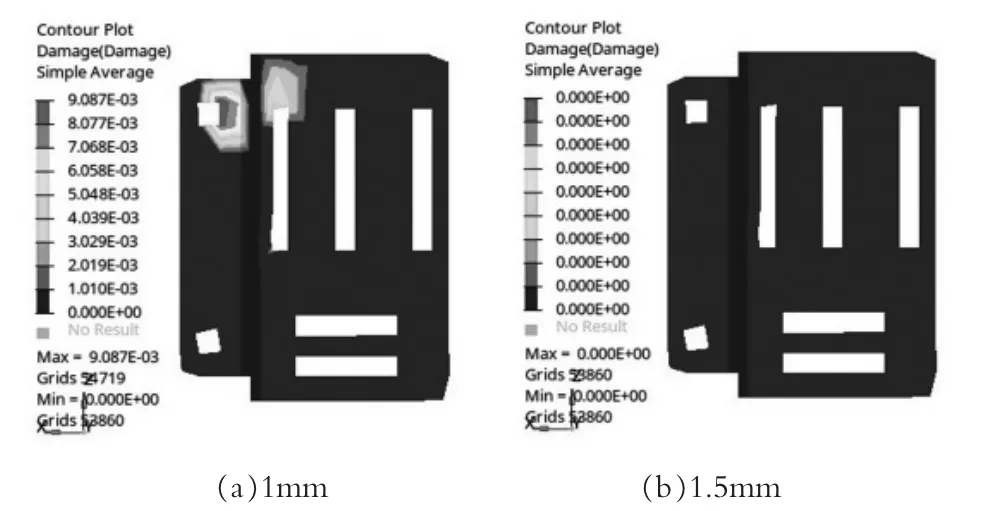
图1 电源固定板损伤情况
3 试验验证
隧道灯固定在振动台上进行3g加速度振动。振动试验完成后,1mm电源固定板发生断裂。排除螺丝简化为1D单元影响,断裂部位与仿真结果较为相符。而优化设计加厚至1.5mm的电源固定板无损伤,表明通过有限元分析可以有效改进现有设计,对试验结果进行预判。
4 结论
本文通过HyperMesh建立了隧道灯有限元模型,利用OptiStruct求解器分析了电源固定板的振动疲劳特性。
(1)1mm厚的电源固定板发生疲劳断裂,与振动试验结果相符。1.5mm厚的电源固定板无疲劳损伤,振动试验结果亦如此,试验结果验证了仿真分析的有效性。
(2)有限元振动疲劳仿真分析能减少打样验证次数,节约成本,缩短开发周期,对振动疲劳类零件的设计具有一定的指导意义。

