旋转轴应变遥测数据压缩技术研究

赵增印，弓 宇，吴 哲，韩肖君

（1.北京航宇天穹科技公司，北京 100043；2.中机生产力促进中心，北京 100044）

0 引言

旋转部件是风力发电系统的重要部件，需要实时监测这些部件的运行状态，以确保风力发电系统旋转部件运转正常。由于旋转部件的特殊性，遥测系统在获取转子的测量参数后通常需要采用无线通讯设备进行高效率、高可靠性的传输，方便地面人员接收数据并进行判读。

旋转部件的高速参数遥测系统属于典型的时域系统，需要实时、快速地传输测量参数[1]。不同设备采集信号带宽和采样速率有差异，以设计的12点测量系统为例，滤波带宽1.2KHz，采样率3.1Ksps，精度16bit，总体数据速率为595200bps，这表明在单位时间内需要传输的旋转轴应变测量数据量非常大。在无线传输信道带宽有限的情况下，为了满足最大传输测量参数数据的要求，在传输旋转轴应变测量数据之前需要压缩时间区间和频谱区域[1]。

本文以旋转部件12路参数遥测系统遥测数据为研究对象，通过对旋转轴应变测量数据特征进行研究，设计一套专用于旋转轴应变测量数据的信源压缩方案，降低其对信息通信带宽需求，解决遥测升级后数据传输带宽不足问题。

1 旋转轴应变测量数据获取及数据特征

1.1 旋转轴应变测量数据采集和传输

旋转轴应变测量数据应变遥测系统主要包括应变传感器、信号放大滤波器、A/D转换器、数据合路器和无线传输单元等，见图1。

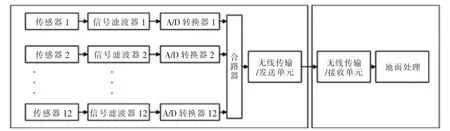
图1 应变遥测数据传输框图

分布在旋转轴相应测量点的应变传感器产生应变测量信号，经适当放大和滤波后，形成需要的测量信号，确保合适的信号取值范围，然后进行A/D转换，进而实现模拟信号到数字信号之间的转换，同时进行数字滤波，完成信源数据采集。然后各测量点产生的数字信号按照一定规则串行化合路，最后通过无线数据传输模块进行旋转轴应变测量数据的发射，完成数据发送。

无线接收单元接收到相应的编码数据后，传输到地面处理系统进行后续解码处理。在旋转轴应变测量数据的传输过程中，通过信源编码技术和信道编码技术对数据进行编码。其中信源编码技术保证无线传输通道带宽能够充分被旋转轴应变测量数据利用，信道编码技术保证地面设备能够正确无误地接收旋转轴应变测量数据[1]。

1.2 旋转轴应变测量数据特征

旋转轴有转动和停止、正向旋转和反向旋转、加速和减速等状态，尤其是对于风电系统，有风强度瞬变和风向瞬变等，因此，数据呈现出非稳定的瞬变特征。

应变数据与其它数据有显著区别，一般变化缓慢，干扰严重。旋转轴应变测量数据不仅具有数据量大、冗余度高的特点，而且具有其独特的规律。从接收的数据看，旋转轴应变测量数据普遍数较小，见图2。

图2 12点应变测量数据

图2中横向为12路采集某一时刻数据，共24字节，每两个字节表示一路样点，16位有符号short类型表示（第 一 排 样 点 数 值 分 别 为：-31，8，-49，-14，41，-18，10，10，18，21，-47，-2）。纵向为各路不同时刻样点，可以看出，每路样点数值随时间变化比较小。以波形的方式画出应变数据见图3。

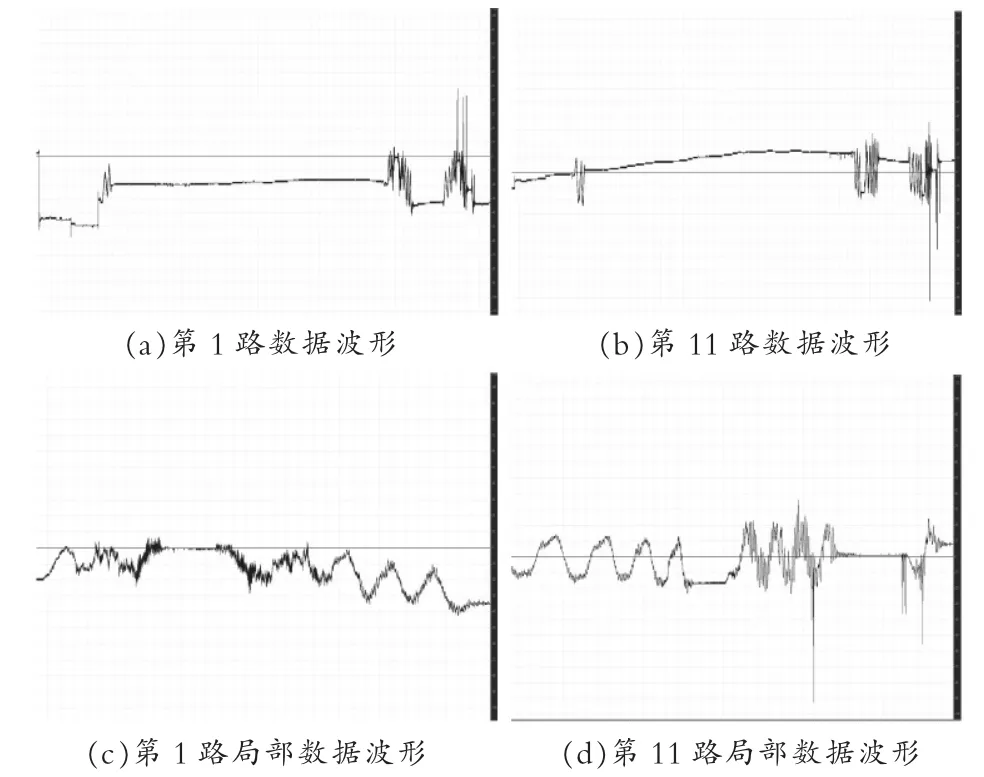
图3 部分应变数据波形图

针对上述旋转轴应变测量数据特征，设计先使用预测方法，然后对预测残差采用霍夫曼压缩编码算法，会有效地减少传输数据总量，满足通信带宽要求。

2 旋转轴应变测量数据压缩算法

2.1 压缩模式选择

数据压缩模式很多，分类方式多种多样。可以根据信息丢失情况分为有损压缩和无损压缩两大类，也可以根据实时性要求分为实时压缩和非实时压缩。为了保证信息完整和时效性，系统设计采用实时无损压缩。

2.1.1 无损压缩技术

目前主流无损压缩算法包括霍夫曼编码、算术编码等。

霍夫曼编码是霍夫曼在1952年提出，霍夫曼编码[2]首先统计输入信号中符号出现的频率，然后按照符号出现频率大小对符号排序，最后构造二叉树为所有符号分配不同长度的码字，其中符号分配的码字越短表示其出现的频率越高。

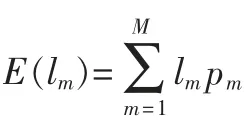
步骤1：待编码信号中的m个符号按概率由大到小进行排序，确保上面符号的概率大，下面符号的概率小，将这些符号作为二叉树树叶，保证pk≤pk+1。

步骤2：两片概率最小的树叶连接一点，作为一个新符号，其概率是两片树叶的概率之和，即p1，2=p1+p2，然后对新符号和剩余符号共m-1个符号进行编码。

步骤3：重复步骤2中的方法，再次对m-1个符号中两个概率最小的符号连接一点作为新符号，然后对新符号和剩余符号共m-2个符号进行编码，按照上述方法一直循环直至树根，最后可通过树根的概率是否为1进行检查。

步骤4：将0和1赋值给每个节点的树枝，从树根开始取每片树叶所经过的树枝上的值，依次排列作为各个符号的霍夫曼码字。

霍夫曼编码码字是异字头码，能够保证编码结果的唯一可译性；由于霍夫曼编码采用符号码字字典，接收端出现误码时只影响当前符号解码，不会影响后续符号解码，可靠性强。

算术编码[3]同样基于统计概率进行编码，编码器也需要先将输入信号中的符号进行出现概率统计，然后按输入信号符号出现的顺序在编码区间上按概率进行区间的划分表示。与霍夫曼编码中每个字符采用整数个位的码字表示不同，算术编码方法是将待编码的输入信号的符号串表示成[0，1）区间上的一个浮点数。输入信号的符号序列越长，算术编码最终划分的区间长度越小，而区间需要更多的位数进行表示。由于计算机的精度的限制，算术编码通常需要使用比例缩放进行区间表示。算术编码过程实际上就是依据输入信号符号的发生概率划分编码区间的过程，与霍夫曼相比，可以获得更高的编码效率。

算术编码器将整个输入信号的符号序列表示为一个在间隔[0，1）中的实数码字，因此解码器需要接收到这个实数的所有位的数据才能进行解码，这也暗示着算术编码对错误很敏感。算术编码的编、解码计算复杂度要明显高于霍夫曼编码，这也决定了算术编码的实时性不如霍夫曼编码。

综合对比，为了实时无损压缩旋转轴应变测量数据，选择霍夫曼编码方法进行旋转轴应变测量数据的压缩。

2.1.2 基于预测和霍夫曼编码的旋转轴应变测量数据压缩方法

由于旋转轴应变测量数据具有缓变的特征，为了进一步压缩数据，可以先采用线性预测的方法，用已有的数据预测未来的数据，使预测误差形成残差数据，将信源信息在零附近进行有效集中，使得符号的概率分布发生集中变化，降低数据的信息熵，从而有利于提高霍夫曼编码的压缩倍数。

由于旋转轴应变测量数据的预测过程会带来信息时延，为了保证实时性，需要降低预测级数。每一级的预测延时是一个样点的采样时间，因为采样速率比较低，样点间隔时间比较长，所以预测的级数不能太高。图4为一阶预测后残差数值的波形。

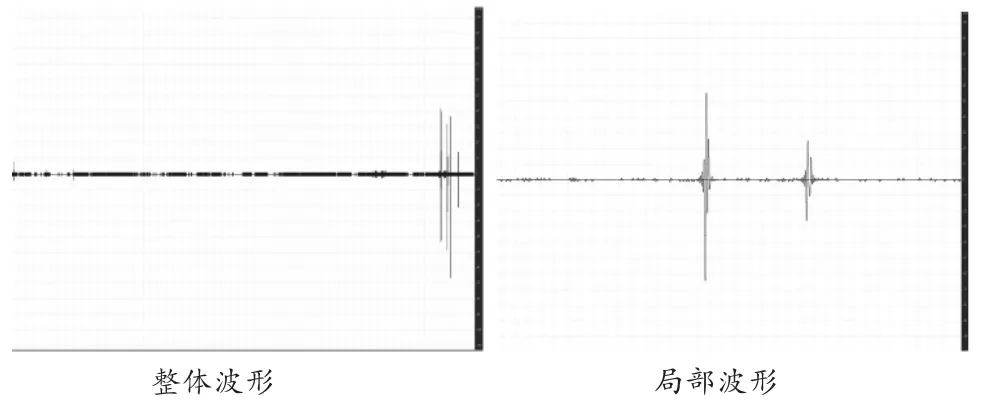
图4 预测后残差数据波形

从图4可以看出，经过一阶预测，旋转轴应变测量数据数值很好的集中在零点附近，分布严重失衡，非常不均匀。当信源的概率分布的不均匀程度越大，霍夫曼编码压缩的效果越好[4]。

为了减少设备的复杂性，设计选择使用经验霍夫曼压缩。经验霍夫曼压缩基于信息熵，依赖于统计方法。

2.2 压缩编码和传输过程

通过上述讨论，设计选择简单实用的线性预测和经验霍夫曼编码对旋转轴应变测量数据进行压缩。在编码端，旋转轴应变测量数据的信源数据先进行一个样本的延时，前一个数据作为的预测值，两者相减得到预测残差，然后利用霍夫曼编码方法对预测残差进行压缩得到压缩后的数据，最后进行无线传输。在解码端，地面接收到压缩数据后，首先进行霍夫曼解码，得到预测残差，然后与预测残差相加得到恢复的信源数据，见图5。

图5 压缩和解压缩框图

2.2.1 信源数据各路独自进行预测。

对旋转轴应变测量数据预测后的残差数值进行频次统计，统计结果见表1。

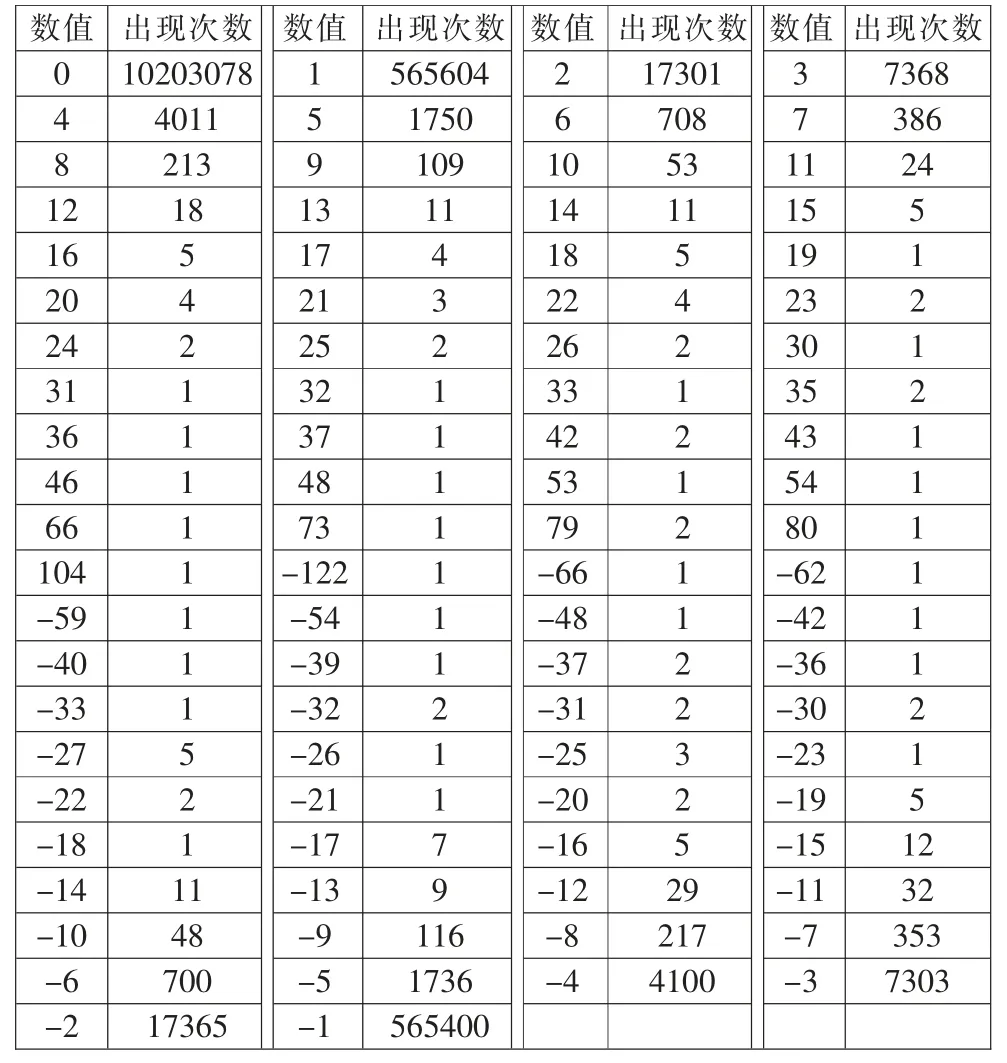
表1 残差数据频次统计

2.2.2 确定霍夫曼编码符号数和对应的频次

根据表1计算各符号对应频次，如表2所示。其中，⊿表示所有大于9，小于-9数值的之和对应的符号。

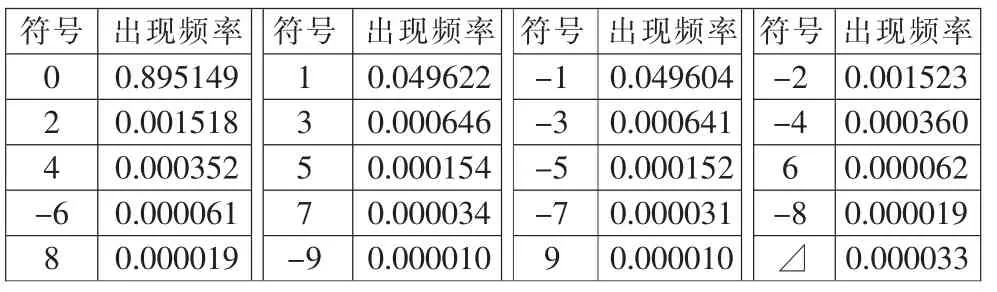
表2 霍夫曼编码符号与对应频率

2.2.3 霍夫曼编码

根据各符号出现的频次进行霍夫曼编码，形成霍夫曼编码表，见表3。

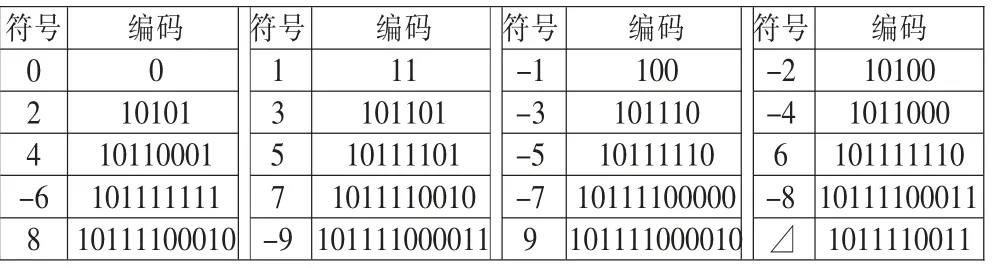
表3 经验霍夫曼编码符号编码表

2.2.4 霍夫曼压缩

按照流程图5给出的过程，对每个样点进行预测，并按照霍夫曼码表对残差数据进行编码，完成数据压缩。⊿为转义标识符号，对残差数据大于9，小于-9数值编码时，先输出⊿编码，再加上输出16位数值源码，形成压缩数据流进行传输发送。

2.2.5 解压缩

地面接收到的数据按照霍夫曼码表进行解码，恢复出残差数据。然后通过已恢复样点的数据，结合预测数据，恢复出该样点数据，完成数据解压缩。

3 仿真结果分析

利用提出的算法进行旋转轴应变测量数据的仿真测试实验，测试旋转轴应变测量数据的总传输数量为22799496字节，其中包括12路，每路数据949978字节，474989采样点。压缩后的数据量为1678134字节，平均码率约43809bps。

提出的算法使用了一阶预测，延时一个样点，实时性非常好。由于使用一阶预测，算法复杂度非常低，实现简单；整数运算，对处理器要求很低；算法使用经验霍夫曼压缩方法，只使用查表运算，实现起来也非常简单。算法使用无损压缩，无失真。

该压缩方法对出现极少的大数值，采用源码传递，未进行压缩，且需要添加转义标识⊿编码，数据长度非但没有压缩，还增加了数据传输量，这会增加数据传输抖动。实际数据如果连续性差，出现突变或者有突发强干扰信号，就会出现数据突变，预测后就会出现大数值数据。为了防止这种现象发生，输入端应有良好的滤波。

由于使用了预测编码方法，传输差错会出现偏心（零点偏移）问题。通过传输时定时插入原始数据进行解决，利用⊿转义标识符号后加原始真实数据实现纠偏。

经验霍夫曼编码需要长时间大量数据统计，形成的码表才具有代表性。要得到一个稳定可信的码表，还有很多工作要做。

4 结论

本文分析了旋转轴应变测量数据的特点，针对其特点设计了一种简单实用的压缩方法，经实验证明能够满足实际工作需求。同时通过以上分析不难看出，该压缩方法仍有很大的改进空间，可以进行继续研究。