水利-交通联合枢纽工程中水闸底板设计优化分析研究
陈 敏,庄梦如,王明东,朱潇潇
(淮安市水利勘测设计研究院有限公司,江苏 淮安 223005)
水工建设中探讨工程设计参数的最优性对提升设计水平、工程质量及运营效率均具有重要作用[1-2],研究水工设计参数最优性可从方案对比、利弊性、工程建设必要性等角度考虑。邓燕[3]、刘中峰等[4]、崔忠[5]根据水工模型试验理论,设计不同方案的模型试验,如溢洪道、消能池及闸门等,对水工模型应力状态、渗流特征开展评价分析,进而确定工程设计参数的最优性,为工程建设提供重要参考。也有一些学者认为工程设计最优化不仅仅需要考虑结构安全可靠性,同样需要考虑结构材料的稳定性,根据结构材料的力学稳定性或渗透特征影响因素[6-8],设计最适配于工程的最优参数,进而为工程最优化设计提供重要基础。不可忽视,模型试验成本较高,而结构材料设计最优化与工程适配性还有待检验,故一些学者认为利用COMSOL[9]、ABAQUS[10]、ANSYS等[11]数值仿真软件分析有限元模型在不同设计方案下应力、位移特征的差异性,为工程设计提供可靠依据。本文根据淮安水利-交通联合枢纽性水闸工程的闸室底板厚度参数最优化问题,开展了不同厚度参数方案的静力与渗流特征分析,为闸室工程的设计提供参考。
1 工程概况
为保障淮安地区水利资源利用效率与河道交通快捷性,考虑在淮涟一干河新建一水利枢纽工程,该工程不仅可对水资源进行峰、谷调度,也可作为通行交通枢纽,缓解河道两岸通行拥堵问题,有效提升一干河周边水利-交通协调性。该枢纽工程主要水工建筑包括有水闸、围堰、交通桥、排沙闸、启闭机等设施,该水闸枢纽工程为多孔式结构,共有8孔,按照四孔并联式设计形式,单孔净宽为6.0 m,闸顶高程为32.6 m,底板长度与厚度乃是根据工程最优设计分析的对象,水闸上游正常蓄水位为12.5 m,枯水位为4.8 m。该水闸支撑结构体系为预应力锚固墩,每个支撑墩直径为1.6 m,在闸墩同一侧中均布置有横、纵连系梁,可有效提升闸墩抗拉特性。根据预埋传感器监测表明,墩身最大拉应力不超过1.2 MPa,位移以沉降方向为主,最大位移量为8 mm;而渗流监测表明闸室内渗流场较平静,无紊流、涡流等现象,蓄水工况下紊动能分布在6.5~10.4 m2/s2,闸室侧壁上静压力分布较稳定,无显著压力集中效应;另一方面,正常蓄水工况下闸室内流速较稳定,基本在4.5 m/s左右,水利冲刷作用并不显著,有效延长水闸使用周期。围堰采用黏性沙土为堆筑料,采用分层压实方法,有效降低土体沉降对堆筑围堰稳定性的影响,围堰与水闸间具有水利缓冲地带,可作为消能降冲的水工建筑设计区域,此与闸室底板渗流、排沙降淤具有密切相关联系,该工程中所设修建的排沙闸主要降低过闸水流含沙量,水文资料显示过闸断面水流含沙量低于2.5 kg/m3。交通桥布设在闸室与启闭机连接中部,宽度为4.2 m,且与交通桥相对应设置有检修桥,宽度为2.2 m。闸室配备有平面钢闸门,并且采用压杆支撑结构体系作为闸门与启闭机之间联动载体,杆件主要以受压为主,最大抗压应力可达18 MPa,启闭机采用液压程序控制,开度与流量匹配性较大,确保闸门防渗效果与过闸流量相结合;根据现状对闸门运营工况下模拟分析得知,其浸润线分布较安全,最大拉应力仅为0.78 MPa,压应力分布满足设计要求。为确保该水闸设计方案适配水利与交通枢纽功能作用,势必需要讨论水闸设计方案对交通桥及闸室静力稳定性影响,因本工程中水闸设施闸顶、侧壁部分设计参数均已确定,故重点探讨闸室底板设计参数的影响问题。
2 设计仿真
根据前述水闸水利-交通枢纽地位与作用性,本文采用Abaqus仿真计算平台对该水闸结构进行有限元建模[10-12],另在计算模型中施加静水压力、扬程压力等,其他结构自重按照均布荷载施加至模型中,研究工况以上、下游水位为正常蓄水位,下游水位为5.6 m。水闸结构按照实际材料本构模型方程进行设定应力变形关系,闸基础影响深度按照试测法确定为26 m,模型横向轴线研究长度为8 m,地基与土层间采用薄层界面单元,土体物理力学状态参数以室内试验测定砂土力学参数取值。
经Abaqus划分网格后,且在闸室底板、闸墩部位等处加密划分,本模型所采用的微单元体为三角形与四边形网格,该计算模型划分后共获得微单元体168 262个,图1为该模型二维特征。根据水利-交通枢纽功能设计前提,该水闸模型顶部为水平向单个自由度边界体系,而底部为零自由度边界条件,闸室侧壁为法向约束条件。为分析方便,本文设定计算模型的X、Y、Z正向分别为水流下游端、结构垂直上方及横轴下右方。

图1 水闸有限元模型
3 闸室底板厚度设计与应力特征关系
根据对闸室底板厚度设计分析可知,其厚度分布范围不得超过单孔净宽1/4,同时其厚度不得低于0.70 m,故本文探讨闸室底板厚度最优设计方案时设定为0.70 m、0.85 m、1.00 m、1.15 m、1.30 m、1.45 m,对各方案的应力、位移特征及渗流特征进行对比,为评价设计最优性提供依据。本文根据水利与交通枢纽工程,重点探讨不同方案中水闸上交通桥底与闸室耦合部位、检修桥与闸室耦合部位、闸室底板部位三个关键部位的应力位移特征,评价最适配闸室底板厚度设计参数,各关键部位所在位置如图2所示。
3.1 拉应力特征
根据对各底板厚度设计方案影响水利-交通联合枢纽工程设施应力分析,获得关键部位最大拉应力与底板厚度变化特征,如图3所示。由图3可知,该水闸关键部位中拉应力最大为交通桥底部位,其拉应力分布为1.68~5.63 MPa,而各方案中检修桥底与闸室底板部位最大拉应力较前者具有差幅40.4%~82.4%、13.1%~31.9%,特别是在底板厚度1.45 m,检修桥底、与交通桥底部位处最大拉应力差距最大,达82.4%。分析表明,水闸枢纽设施中,交通桥底所受张拉应力较大,其底部应配置抗拉效果较好的结构材料,增强桥底刚度,保障交通枢纽顺畅。当闸室底板厚度愈大时,交通桥底、闸室底板两关键部位最大拉应力随底板厚度均为先减后增变化,变化节点为底板厚度1.00 m时,在该方案下,前述两关键部位最大拉应力分别为1.68 MPa、1.29 MPa,显著低于结构材料安全允许值;而该方案下交通桥底处最大拉应力相比闸室底板厚度0.70 m、0.85 m分别降低了64.7%、45.5%,在底板厚度0.70~1.00 m区间内交通桥底最大拉应力平均降低40.4%,同样闸室底板部位在该区间内亦具有平均降幅40.7%。当底板厚度超过1.0 m后,交通桥底、闸室底板部位最大拉应力均具有较大增幅,底板厚度1.15 m、1.45 m时闸室底板处最大拉应力较厚度1.00 m时分别增长了56.7%、2.8倍,而在底板厚度1.00~1.45 m区间内其最大拉应力平均增幅可达65.3%,同样在交通桥底处,其最大拉应力在该厚度区间内的平均增长可达51.2%,表明底板厚度超过1.00 m后拉应力的增长敏感程度远高于前一递减区间,从结构应力安全角度考虑[13-14],应避免底板厚度超过1.00 m。相比前两关键部位,检修桥底处最大拉应力受底板厚度参数影响较小,各方案中检修桥最大拉应力分布为0.98~1.00 MPa,最大变幅为1.15~1.30 m方案,达1.8%,各方案中检修桥底拉应力特征值均低于结构材料安全值,故闸室底板厚度设计优化时,可不考虑检修桥底拉应力所受影响。

图3 关键部位最大拉应力与闸室底板厚度关系
3.2 压应力特征
计算该枢纽工程水闸底板厚度各设计方案应力时,可联合枢纽工程中交通、水利功能的关键部位压应力变化特征,如图4所示。从图4中可知,该枢纽工程中闸室底板压应力为最高,各方案中分布为4.00~9.52 MPa,而交通桥底、检修桥底部位处最大压应力较前者分别具有差幅20.8%~29.8%、47.3%~76.5%。当底板厚度增大时,闸室底板、交通桥底部位最大压应力分别为递增,但增幅在减小,特别是在底板厚度1 m后,其压应力增长能力基本达到“饱和”状态,两关键部位最大压应力在该方案后基本稳定在9.5 MPa、6.8 MPa;当底板厚度为0.70 m时,交通桥底最大压应力达3.19 MPa,而厚度为1.00 m、1.30 m、1.45 m后相应的压应力较前者分别增长了1.080倍、1.140倍、1.138倍,在厚度0.70~1.00 m 区间内压应力平均增幅可达46.8%,而超过1.00 m后,其压应力增长平缓,最大增幅为2.1%,平均增幅仅为0.98%;闸室底板部位处最大压应力与之变化特征基本一致,在厚度0.70~1.00 m与1.00~1.45 m区间内分别具有平均增幅54.80%、0.13%。压应力的增长,表明结构抗滑移效果增强,故底板厚度1 m后,交通桥底、闸室底板处结构抗倾覆特性达到稳定。在底板厚度影响压应力特征中,检修桥部位处最大压应力仍然无显著变化,在方案0.70~0.85 m具有最大变幅3.4%,各方案最大压应力分布为2.12~2.29 MPa。综合拉、压应力特征可知,底板厚度设计时应重点考虑交通桥底与闸室底板部位,检修桥拉、压应力特征均满足安全设计要求,从本文各方案应力对比结果可知,当闸室底板厚度为1.0 m时,应力特征最佳,设计效果最优。
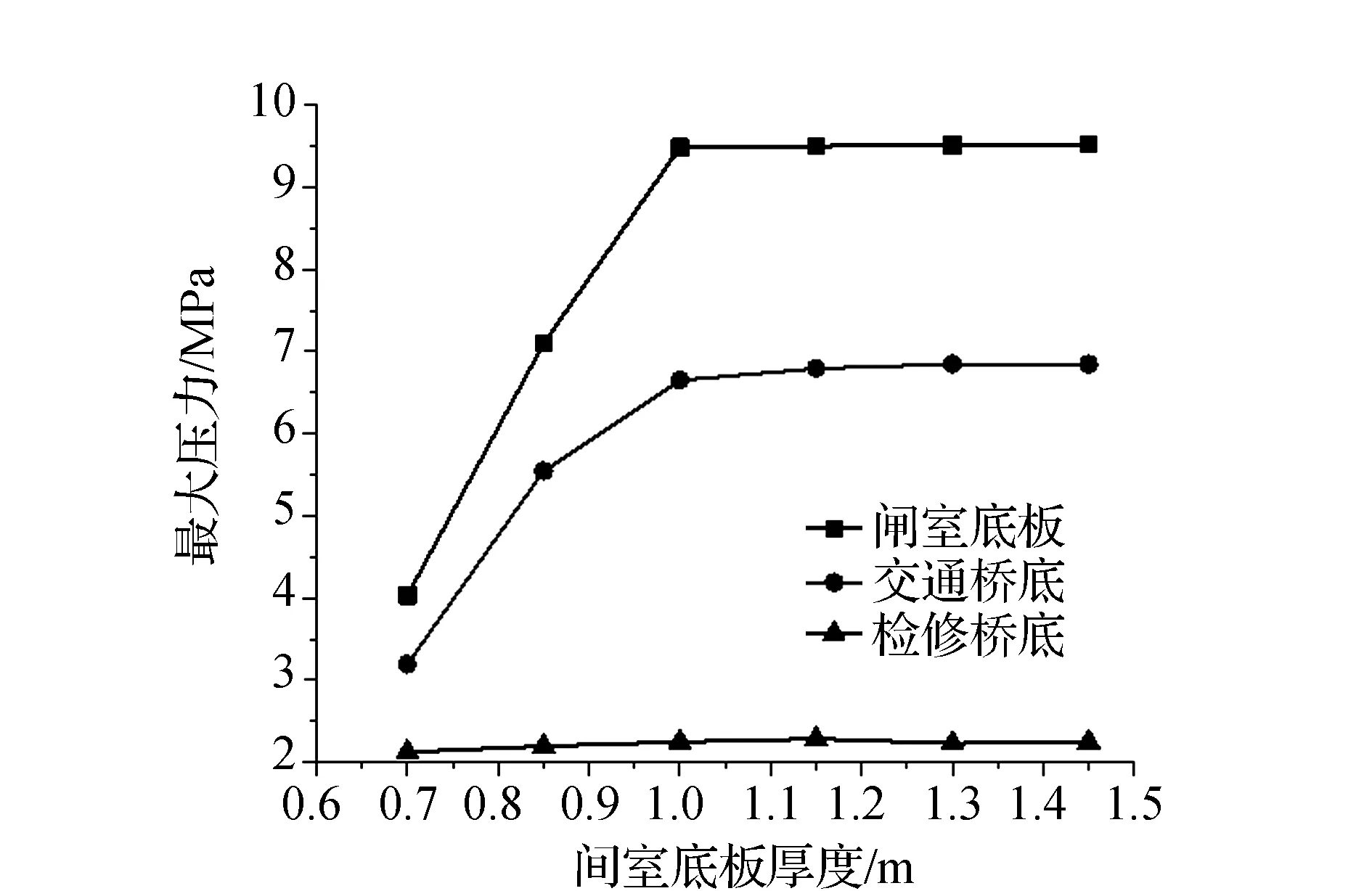
图4 关键部位最大压应力与闸室底板厚度关系
4 闸室底板厚度设计与位移、渗流特征关系
4.1 位移特征
根据对闸室底板厚度设计方案的静力特征计算,可获得水闸各向位移与底板厚度关系,如图5。从图5中曲线变化关系可知,水闸位移主要以竖向沉降为主,其Y向位移在各方案中分布为6.77~14.60 mm,而水闸横向轴线Z向位移量变化幅度较小,基本稳定在3.95 mm,不受底板厚度参数影响。当底板厚度愈大,水闸竖向沉降、顺水流方向上位移均有降低态势,表明增大底板厚度,有助于降低水闸变形量,提升结构稳定性[15-16]。从底板厚度参数抑制Y、X向位移来看,当底板厚度为0.70 m时X向位移为11.9 mm,而在厚度0.70~1.00 m区间内平均降幅可达33.5%,超过1.0 m后降幅迅速减小,后平均降幅仅为1.2%;同样在Y向位移中亦是如此,六个方案中平均降幅为13.1%,但在厚度0.70~1.00 m 与1.00~1.45 m区间内位移平均降幅分别为31.40%、0.85%。分析认为,从结构设计经济性考虑,当闸室底板厚度1.00 m时,结构位移量值已处于较低水平,超过该厚度后水闸位移值抑制特性较弱,故选择底板厚度1.00 m为设计方案时,位移特征满足水闸交通-水利枢纽安全要求。

图5 水闸各向位移与闸室底板厚度关系
4.2 渗流特征
基于各厚度设计方案下水闸渗流计算,获得典型方案下水闸剖面孔隙压力分布特征,如图6所示。从图6中可知,改变闸室底板厚度,并不影响水闸剖面上孔隙压力分布状态,仅其最大孔隙水压力有所变化,在厚度1.00 m时孔隙水压力最大为230.4 kPa,而厚度0.70 m、1.3 m时最大孔隙水压力较前者分别增长了0.34%、14.10%。基于渗流特征计算获得厚度0.70 m时水闸不均匀系数为2.255,而厚度1.00 m时不均匀系数为1.552。综合分析认为,闸室底板厚度1.00 m为最佳设计方案。

图6 孔隙压力分布特征
5 结 论
(1)水闸中拉应力最大为交通桥底部位,检修桥底、底板部位最大拉应力与之差幅为40.4%~82.4%、13.1%~31.9%;交通桥底、闸室底板最大拉应力随底板厚度均为先减后增变化,厚度1.00 m 时为最低,为1.68 MPa、1.29 MPa,且拉应力递增区间受厚度参数影响敏感度高于递减区间;检修桥底处最大拉应力受厚度参数影响较小,分布为0.98~1.00 MPa。
(2)闸室底板压应力为最高;底板厚度增大时,闸室底板、交通桥底部位最大压应力递增,但增幅在减小,特别是厚度1.00 m方案后压应力基本稳定,闸室底板在厚度0.70~1.00 m与1.00~1.45 m 区间内平均增幅分别为54.80%、0.13%;检修桥底压应力变幅较小,稳定在2.12~2.29 MPa。
(3)水闸位移主要以竖向沉降为主,Z向位移量稳定在3.95 mm,不受底板厚度参数影响;Y、X向位移随底板厚度递减,但厚度超过1.0 m后位移降幅较小,在厚度0.70~1.00 m区间平均降幅分别为31.4%、33.5%,而在厚度1.00~1.45 m 区间为0.85%、1.20%;厚度参数不影响孔隙水压力分布,其量值以厚度1.00 m方案下为最优。
(4)综合应力、位移与渗流特征,认为闸室底板厚度1.00 m时结构安全可靠性最强、设计最优。

