基于FDA的居民用户空调用电行为分类分析方法

白东壮，田世明，邹毅豪，周 颖，徐玉婷，韩凝晖，李永军

（1.中国电力科学研究院有限公司，北京 100192；2.需求侧多能互补优化与供需互动技术北京市重点实验室，北京 100192）

0 引言

由于当前城市化进程发展迅速，城市居民对各类电器的需求增加，尤其是居民对空调的需求。我国夏季时间较长，居民长时间使用空调。居民各类电器中空调使用的阶段性极强，从而导致城市供电网负荷阶段性增加，给电力系统平稳运行带来了不小的隐患[1]。用电行为包含了电力用户在外界环境影响下进行的用电活动及背后的行为规律，可以通过管理手段使得全社会用电量趋于平衡[2-3]。因此对居民空调用电行为进行分析尤为重要。目前很多专家学者均提出不同理论方法的居民空调用电行为分析方法，陆俊等人[4]提出一种基于极限学习机算法的用户用电行为分类方法。在前期用户行为的特征优选策略的基础上，采用特征优选策略提取负荷曲线的最佳特征集对用户用电数据进行分类分析，但该算法在提取居民用电优选级时，并未考虑时间序列问题，导致极限学习机算法输出的分类结果精度不足。冯志颖等人[5]提出一种考虑负荷纵向随机性的基于推土机距离的用户用电行为识别新方法。该方法通过统计电力用户同一时刻多天的负荷分布情况，从横向和纵向2 个角度全面表征用户的用电行为，但该方法仅针对电网负荷变化情况作了居民用电行为分析，家用电器用电时间和季节不同对电网造成的负荷也不尽相同，由此该方法具有一定的片面性。面对当前居民空调用电行为分析方法存在的问题，提出基于非介入式的居民空调用电行为分类分析方法，为电网安全运行提供更高的保障。

1 居民空调用电行为分类分析

1.1 居民用电行为特征提取

针对居民用电行为，使用多重分形方法[6]提取居民用电行为特征。多重分形方法是非线性科学的分支，是一种分为多个区域的复杂分形结构。为了对分形的复杂性和不均匀性进行更细致地刻画，需引进它的概率分布函数及其各阶矩的计算。利用该方法进行特征提取时，使用计算盒子数方式将复杂的数据分为具备不同奇异度的小区域，使数据的特征表达更为充分。使用多重分形方法提取居民用电行为特征详细流程为：

令居民用电行为标准化数值为1，使用盒子对居民用电行为实施覆盖处理，盒子的尺度由ε表示，ε≤1。经过盒子对居民用电行为覆盖后，每个盒子内存在n个居民用电行为。计算第i个盒子内用户用电行为概率测度Pi(ε)，即：

式中：Ii为居民用电行为总数，i=1,2,…,m。

令ψq(ε)表示配分函数，使用该函数获取居民用电质量指数，且该配分函数可作为式（1）的s阶矩，s表示权重因子。配分函数ψq(ε)为：

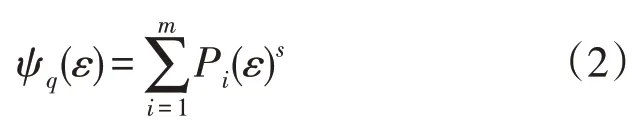
τ(s)为质量指数，其表达式为：

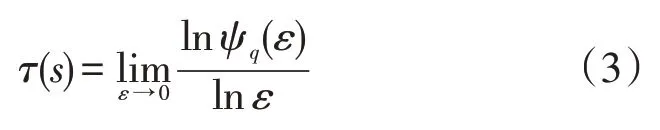
特征选择的合理与否对聚类结果准确性有重要影响[7]，多重分形方法在进行特征提取时，使用指数和奇异多重分形谱描述居民用电行为特征，二者分别由α(s)，f(α) 表示，奇异多重分形谱使用Legendre 转换得到[8]：

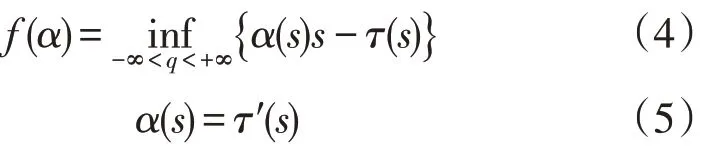
式中：τ′为特征集。

将式（3）结果代入到式（5）中可得到指数α(s)数值，该指数数值可描述居民用电特征的局部奇异性。而奇异多重分形谱则可描述居民用电特征的完整奇异性，且特征参数分布的统计结果同样反映出空调行为驱动特性的个体差异[9]。依据式（4）与式（5）结果可获取居民用电特征的局部奇异性和完整奇异性，由此得到居民用电特征。

1.2 基于FDA的用电行为聚类

使用函数型数据分析算法[10]（Functional Data Analysis，FDA）对居民用电特征进行投影处理后，利用支持向量机算法对居民用电行为进行分类处理，得到居民空调用电行为。FDA 投影的核心思想是通过数据自身具备的连续性与平滑性，利用相应函数表达数据序列，经过FDA 投影处理后的局部用电行为特征信息内不存在聚类噪音点干扰[11]。FDA 投影过程如下：将每个居民用电特征作为观测样本包，令第i个观测样本包内存在的列离散观测数值由yi1,yi2,…,yin表示，使用FDA 投影将列离散观测数值转换为基函数，由于居民用电行为特征不具备周期性，在此使用B 样条基函数[12]描述FDA 投影，令a表示B 样条基函数阶数，ζ(ζl,l=1,2,…,l-1)表示节点序列，则B 样条基函数递归表达式为：

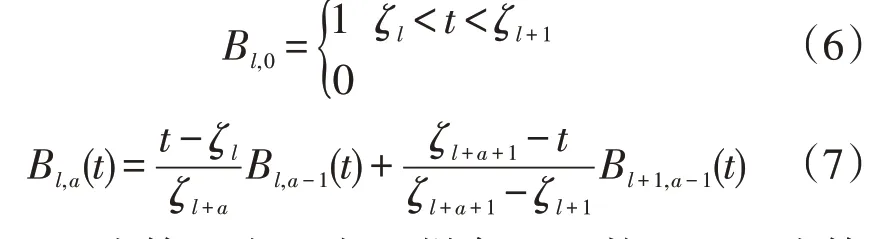
式中：Bl,0为第l个0 次B 样条基函数；Bl,a(t)为第l个a次B 样条基函数；t为自变量[13]。

将FDA 投影系数向量引入到B 样条基函数内，即：

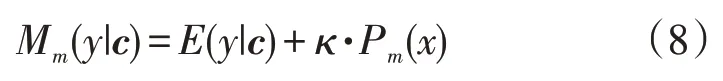
式中:E(y|c)，Pm(x)，κ分别为FDA 投影后的误差平方和、粗糙乘法函数、平滑参数；c为投影系数向量。

使用一次导数方法对式（8）进行求解后，可获取到FDA 投影系数向量数值并将该数值代入到B样条基函数内，完成FDA 投影。

居民用电行为特征观测样本包内的离散观测数值经过FDA 投影处理后，结合FDA 聚类理论，使用支持向量机算法对居民用电特征进行聚类处理[14]，获取居民空调用电行为特征。支持向量机算法是通过在超平面内令类别间距最大的同时保持类别间距离最小的分类实现聚类的方法[15]。通过对居民日常负荷曲线进行聚类，分析其整体的能耗类型和用电特性[16]，使用sigmoid 函数计算多类别样本边界点。

令X表示局部用电行为特征不均衡样本，其正样本集合负样本集分别由表示，其中U+，U-分别表示少类样本点数量和多类样本点数量，且U=U++U-。设置Fisher 判别聚类目标函数[17]为：

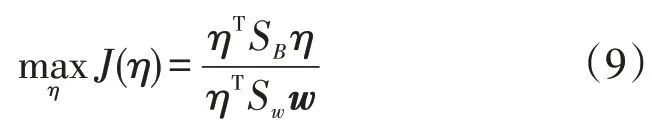
式中：η为投影方向；ω为系数向量；T为训练点集。

其中：

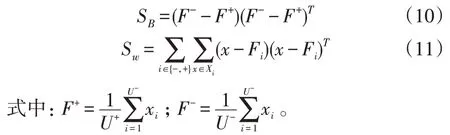
支持向量机在聚类居民用电行为特征时，聚类内的新样本点经过FDA 投影后与包含新样本的少类样本中心距离小于某个正数，为避免聚类新样本点时，其向多类样本集中区间扩散，通过分析将总电力负荷分解为独立电器的用电信息[18-19]，设置聚类约束条件为：

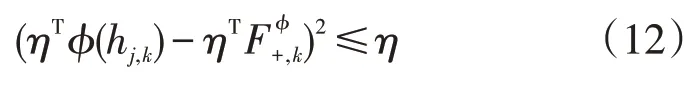
式中：j=1,2,…,zk；k=1,2,…,K；zk为新生成的少类样本点第k个聚类的容量；ϕ为核函数；hj,k为第k个聚类中心的第j个样本点；，其中lk为少类样本点中第k个聚类样本点容量，为少类样本点内第k个聚类内的第l个样本点。

设置符合新生成的靠近多类样本边界点条件，即：

经过式（12）和式（13）步骤不断迭代，拟形成的少类样本与支持向量机的支持向量数量相同，则获取到居民空调用电行为特征。

1.3 基于改进DTW的用电行为分类

动态时间规整（Dynamic Time Warping，DTW）算法是专门处理具备时间序列数据的一种方法，通过对比数据时间序列的相似性判断数据类别[20]。该方法被广泛应用于语音识别、时间序列数据分类等方面[21]。居民空调用电行为特征具备时间序列特征，因此使用DTW 算法对居民空调用电行为特征进行分类。由于在计算居民空调用电行为特征相似度时存在大量根号运算[22]，为使计算过程更加便捷，DTW 算法使用卡方检验算法计算居民空调用电行为特征，详细过程如下：

使用居民空调用电行为特征构建参考模板和待分类模板，分别由R={R(1),R(2),…,R(m)}、Q={Q(1),Q(2),…,Q(m)} 表示，参考模板和待分类模板的特征矢量和维数数值均相同[23]，分别由R(m)，Q(n)表示。参考模板R(mi)和待分类模板Q(ni)的特征矢量的失真量由d[Q(ni),R(mi)]表示，d[Q(ni),R(mi)]为两个矢量之间的欧式距离。获取与多个特征矢量节点相对应的累计失真量，其表达公式为：

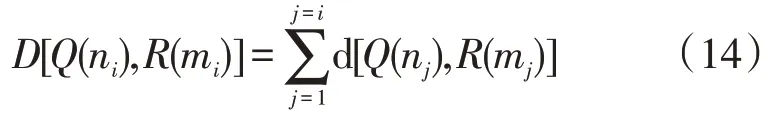
DTW 算法进行分类的目的为计算特征矢量节点的最佳路径，使该路径的累计失真量数值最小[24]。则迭代后的累计失真量表达公式为：

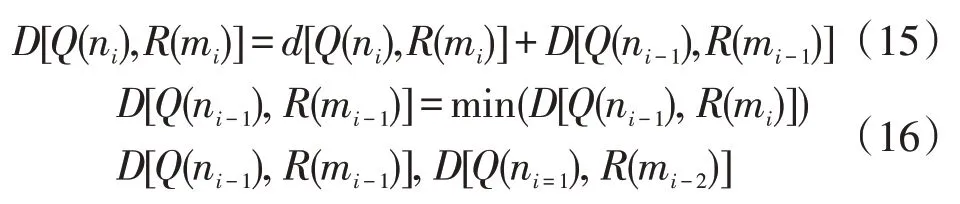
在式（15）-式（16）迭代过程中，受居民空调用电行为时间序列内元素间距离影响，导致对居民空调用电行为分类时，计算特征矢量节点的最佳路径宽松，使分类结果不够精准，在此通过定义矢量编码距离d(t1,t2)，对DTW 算法进行改进，即：

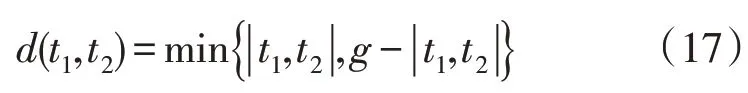
式中：t1表示Q(ni)；t2表示R(mi)；g为居民空调用电行为特征维数。

经过式（14）-式（17）步骤迭代后，得到居民空调用电行为参考模板和待分类模板的累计最小失真量，对比两个模板，相似度接近数值1 的居民空调用电行为即为同一类。

2 实验分析

为验证本文方法实际应用效果，以江苏省某城市非介入式负荷量测设备采集到的近2 年居民用电数据作为实验对象，使用R 语言对本文方法进行仿真分析。非介入式负荷量测设备借助在智能电表中嵌入硬件装置，通过负荷识别算法得到用户内容各类电器的准确信息，比如开停机时间，各时段用电量等[25]。

2.1 特征提取测试

居民用电行为特征提取是分析居民空调用电特征的基础，以配分函数的线性拟合作为衡量本文方法提取居民用电行为特征能力，测试在权重因子数值不同情况下，本文方法提取居民用电行为特征时配分函数线性拟合变化情况见图1。

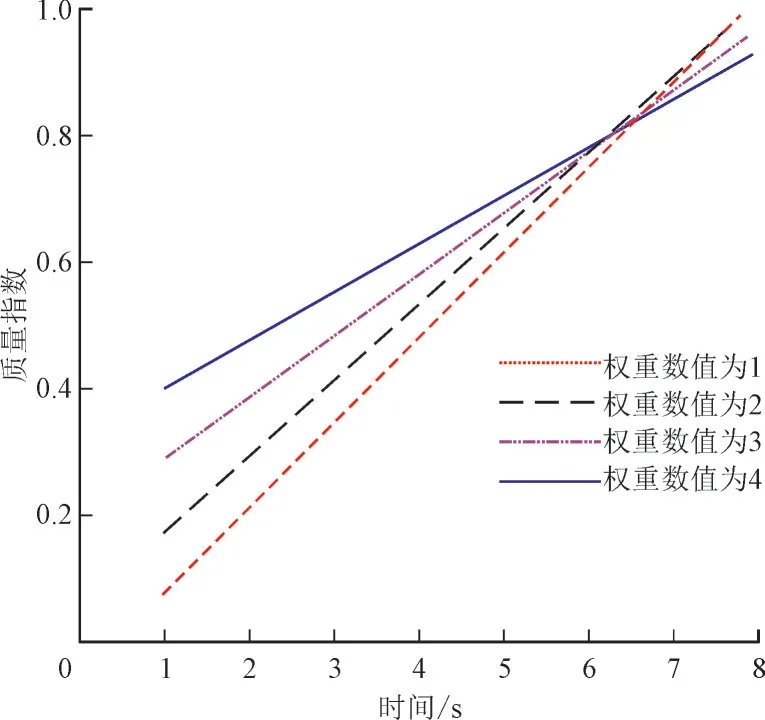
图1 特征提取测试结果Fig.1 Test results of feature extraction

分析图1 可知，随着提取居民用电特征时间的增加，配分函数的质量指数（无量纲）呈现为直线上升趋势。虽然权重数值大小可影响配分函数质量指数数值，但在提取居民用户特征时间为6.5 s 左右时，不同权重数值时的配分函数质量指数达到重合，在提取居民用户特征时间为1～6.5 s 之间，权重数值较大时的配分函数质量指数数值较低且不同权重数值时的质量指数数值差值较大，随着时间的增加，不同权重数值时的质量指数差值逐渐降低，在时间为6.5 s 左右时，其差值为0。当提取居民用电行为特征时间超过6.5 s 后，权重数值较低时的配分函数质量指数数值较大，在特征提取时间为8 s时，权重数值为1 时的质量指数数值达到1.0，权重数值为4 时的质量指数数值为0.93 左右。结果表明本文方法在受权重取值影响较小及质量指数曲线表现为线性关系时，提取居民用电行为特征精度达到了0.93 以上。

2.2 用电行为类别聚类测试

以该市2 000 个居民用电行为数据作为实验对象，使用本文方法对该2 000 条居民用电行为数据进行聚类处理，获取居民冰箱、洗衣机、空调、电视和其他家用电器所占百分比并与实际数量进行对比，分析本文方法对居民用电行为聚类能力，结果如图2 所示。

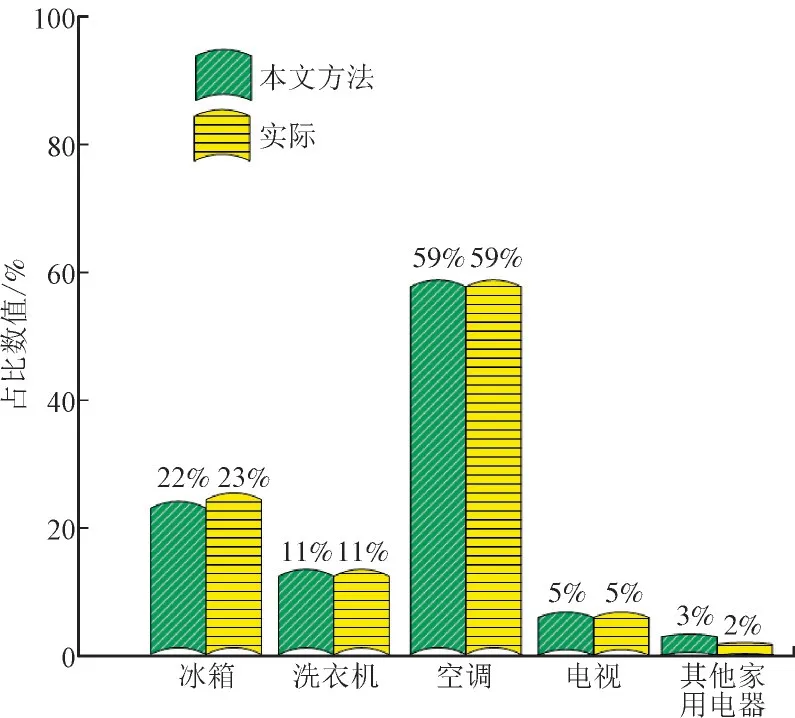
图2 居民用电行为聚类测试结果Fig.2 Test results of residential electricity consumption behavior clustering

分析图2 可知，在该市的2 000 条居民用电数据内，空调占比高达59%，其次依次为冰箱、洗衣机、电视以及其他家用电器。使用本文方法对居民用电数据聚类后得到的该居民用电数据内空调、洗衣机、电视所占比例均与实际数值相同，虽然所有家用电器的总比值与实际比值相同，但在聚类冰箱和其他家用电器时出现较小数值偏差，偏差数值仅为1%。该结果表明本文方法可有效聚类居民用电行为类别且数值较为准确。

2.3 居民空调用电行为分类测试

以失真量作为衡量本文方法分类居民空调用电行为的精度指标，测试居民空调用电特征维数不同情况下，本文方法分类居民空调用电行为精度，为更充分呈现本文方法应用效果，使用文献[3]方法与文献[4]方法与其进行对比。其中文献[3]方法表示极限学习机的居民用电行为分类，文献[4]方法表示用户用电行为聚类方法，结果如图3 所示。

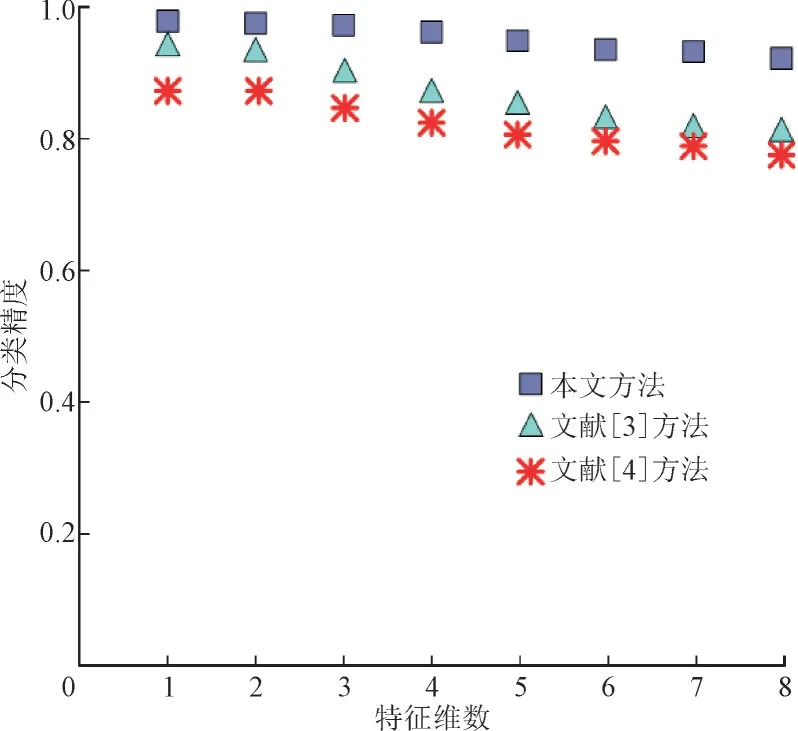
图3 分类精度测试结果Fig.3 Test results of classification accuracy

分析图3 可知，居民空调用电行为特征维数与其分类精度呈反比例关系。在不同特征维数时，本文方法的分类精度数值始终较高，尤其是在特征维数分别为1，2，3 时，本文方法的分类精度接近1.0，而随着居民空调用电行为特征维数的增加，本文方法的分类精度呈现缓慢下降趋势。文献[3]方法和文献[4]方法均在居民空调用电行为特征维数超过3 后呈现下降趋势，且下降幅度稍大，两种方法的分类精度也较本文方法低，表明本文方法分类居民空调用电行为时受其特征维数影响较小，分类精度接近1.0。

分析图4 可知，3 种方法的分类耗时随着数据量的增加而增加。其中文献[3]方法和文献[4]方法的分类耗时曲线随着数据量的增加呈现迅速上升趋势，分类耗时较长，而本文方法在数据量为2 000条之前分类耗时曲线呈现小幅度增加趋势，当数据量超过2 000 条之后其增长幅度相对较大。当数据量为4 000 条时，本文方法较文献[3]方法和文献[4]方法的分类耗时较低，其中本文方法分类耗时仅为8 s。结果表明本文方法在分类居民空调用电行为时可有效缩短其消耗时间。

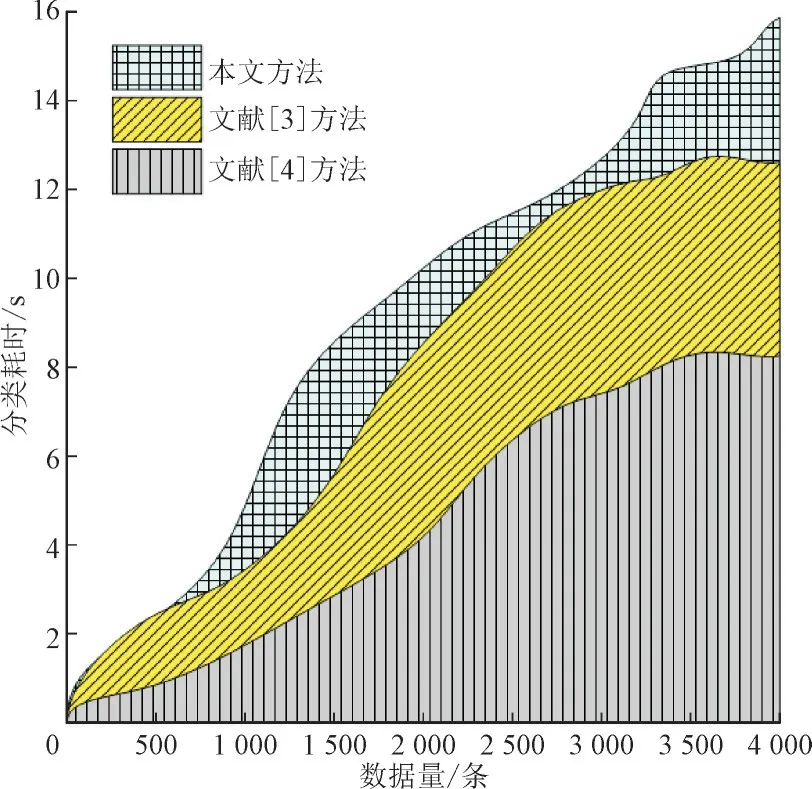
图4 分类耗时测试结果Fig.4 Test results of classification time consuming

2.4 应用测试

以该城市某小区居民8 月份日空调用电情况作为实验对象，使用本文方法对该居民空调用电行为进行分类后，分析该居民用空调用电行为结果如表1 所示。

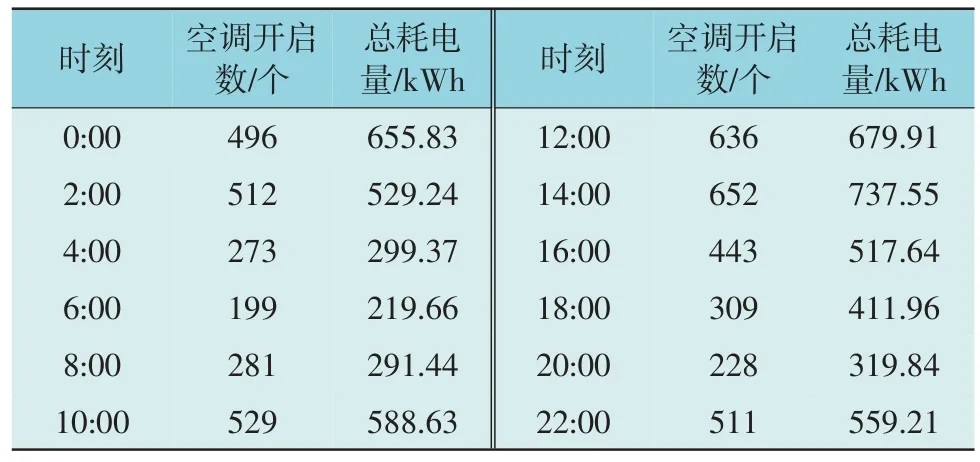
表1 不同时刻居民空调用电情况Table 1 Residential air conditioning electricity consumption at different time points

分析表1 可知，该小区居民同时使用空调的高峰期在上午10:00 至下午14:00 和夜间22:00 至凌晨02:0 之间，说明中午室内温度较高，居民对空调的需求度较强，而夜间开启空调则利用空调控制室内温度平衡，使睡眠环境更为舒适。而在凌晨04:00至上午08:00 之间，室外温度较低使室内外温差降低，此时无需开启空调室内即可达到人体适宜温度数值。而从居民开启空调的耗电量来看，依据当前一级能效的空调来计算，1 台一级能耗空调的耗电量为1.03 kWh，通过计算得到该小区同时开启空调时的耗电量均高于一级能耗空调耗电量的计算值，表明该小区所安装的空调有一部分高于一级能耗，从环保角度来看，该小区的能源消耗量存在一定程度资源浪费情况。

3 结论

针对居民非介入式的居民空调用电行为分类中存在分类分析耗时长，结果不准确的问题，提出基于非介入式的居民空调用电行为智能分类分析方法。该方法将FDA 算法和DTW 算法应用到居民空调用电行为分析过程中，并对DTW 算法运算过程中存在的不足进行了改进，实现了居民空调用电行为分析。同时通过R 语言仿真处理实验对象并进行多角度验证后，得出以下结论：本文方法提取居民用电行为特征时的配分函数质量指数达到1.0，特征提取能力强；对居民用电行为聚类偏差较小且具备分类居民空调用电行为精度高耗时短的特点，可有效获取居民空调开启习惯以及电量消耗情况，具备较好的应用性。