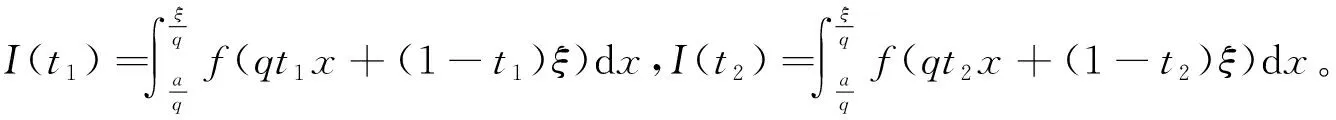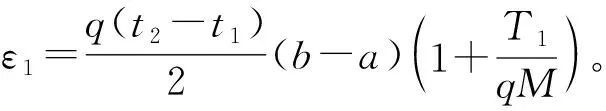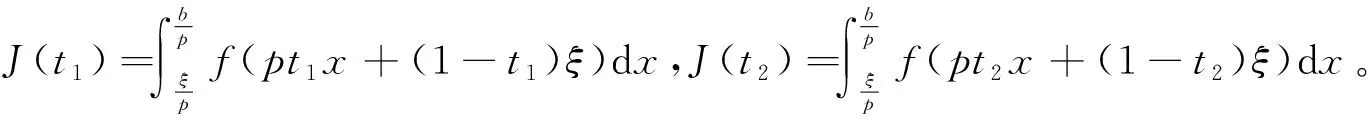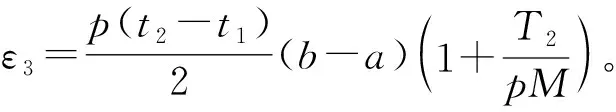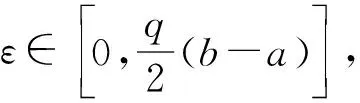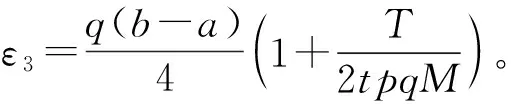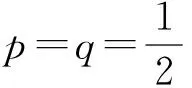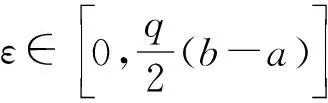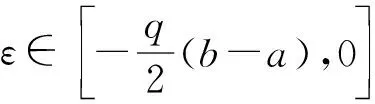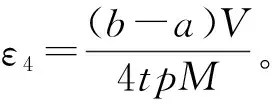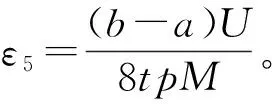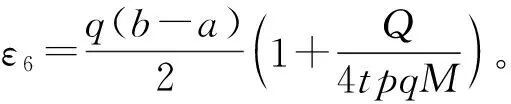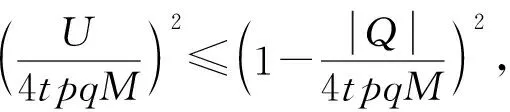由一个Hermite-Hadamard型不等式生成的差的不等式

时统业

(海军指挥学院，江苏 南京 211800)

0 引言和引理

设f是[a，b]上的凸函数，则

(1)

式(1)称为Hermite-Hadamard不等式[1-4]。

定义1设f是定义在[a,b]上的函数，如果存在常数M，使得对于任意x1,x2∈[a,b]，有|f(x1)-f(x2)|≤M|x1-x2|，则称f是定义在[a,b]上的M-Lipschitz函数。

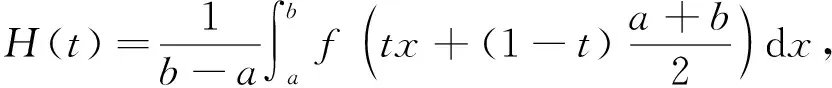
f(pa+(1-p)b)≤C(p)≤pf(a)+(1-p)f(b)，

(2)

其中f是[a,b]上的凸函数，p∈(0,1)，

文献[8]引入了包括C(p)在内的3个加细式(2)的函数，在f是定义在[a,b]上的M-Lipschitz函数时，给出了有关C(p)的不等式。

文献[9]考虑了定义在[0,1]上的函数

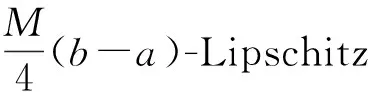
文献[11]引进了另一个与Hermite-Hadamard不等式相关的函数，

其中p,q∈(0,1)，p+q=1，且ξ=pa+qb。

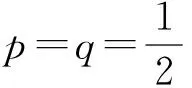
(3)

由式(3)生成两个差值

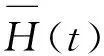
1 主要结果

定理1设f是定义在[a,b]上的M-Lipschitz函数，0≤t1

(4)

其中

先考虑0

再考虑t1=0,t2∈(0,1]情形。

综上所述，对任意0≤t1

(5)

(6)

先考虑0

再考虑t1=0,t2∈(0,1]的情形。

综上所述，对任意0≤t1

(7)

(8)

将式(6)和式(8)分别乘以p和q，然后将所得不等式相加，则式(4)从右边数起第二个不等式得证。利用函数x2的凸性，式(4)右边第一个不等式得证。

推论1设f是定义在[a,b]上的M-Lipschitz函数，0≤t1

推论2设f是定义在[a,b]上的M-Lipschitz函数，则有

定理2设f是定义在[a,b]上的M-Lipschitz函数，则对于任意t∈(0,1]有

(9)

其中

(10)

推论3设f是定义在[a,b]上的M-Lipschitz函数，则对于任意t∈(0,1]有

其中

定理3设f是定义在[a,b]上的M-Lipschitz函数，则对于任意t∈(0,1]有

(11)

其中

(12)

当f是定义在[a,b]上的M-Lipschitz函数时，(-f)也是定义在[a,b]上的M-Lipschitz函数，对(-f)使用已证明的结果则得

故式(11)得证。

定理4设f是定义在[a,b]上的M-Lipschitz函数，则对于任意t∈(0,1]有

(13)

其中

证明当ε∈[0,q(b-a)]时，有

当ε∈[-q(b-a),0]时，有

综上所述，对任意ε∈[-q(b-a),q(b-a)]时，有

(14)

当f是定义在[a,b]上的M-Lipschitz函数时，(-f)也是定义在[a,b]上的M-Lipschitz函数，对(-f)使用已证明的结果得

故式(13)得证。

定理5设f是定义在[a,b]上的M-Lipschitz函数，则对于任意t∈(0,1]有

(15)

其中

q[t(f(ξ)-f(b))+f(tb+(1-t)ξ)-f(ξ)]}。

证明当ε∈[0,q(b-a)]时，有

(16)

推论4设f是定义在[a,b]上的M-Lipschitz函数，则对于任意t∈(0,1]，有

(17)