大坡度阶梯溢流坝掺气水流水深数值模拟研究
王翔宇,刘 懿,林鹏程,邵雨辰
(1.南京市水利规划设计院股份有限公司,江苏 南京 210001;2.浙江水利水电学院,浙江 杭州 310001)
阶梯溢流坝是一种自古有之的泄洪坝方式,这种坝型的坝面与普通溢流坝不同,具有台阶式的形状。经前人研究表明阶梯溢流坝的水流在台阶的极大不平整度的影响下可以大量卷入空气,减少了坝面产生空化空蚀的危害。同时,水体因掺入大量气体剧烈翻滚使得效能效率大幅上升。此外,阶梯的不平整度增大水体的含氧量,因此可以利用其作为改良水质的方法[1]。随着20世纪80年代碾压混凝土技术的巨大进步,阶梯式溢流坝逐渐开始成为一种热门的坝型在水利工程被广泛的使用,与此而来,许多在这种坝型上的水力问题开始被讨论[2]。流量的大小、台阶的尺寸、上游的水头与大坝的坡度都是其中比较重的要的因素[3]。流量大小影响了水流在第一次收缩后到上升的距离和上升的大小;台阶尺寸的大小影响了水流到达全断面稳定掺气的位置所在。在开始掺气到稳定掺气时,水深不断增加,在到达稳定掺气点后之后,水流水深保持不变。通常情况下,台阶尺寸越大,到达稳定掺气点的距离也越长:大坝的坡度对水深也有重要的影响,本次数值模拟试验就重点研究坡度对掺气水深的影响[4]。
本文利用FLOW-3D 软件,通过CAD软件建立40°、53.1°、60°和70°的大坡度接替溢流坝模型导入FLOW-3D软件进行数值模拟计算。对结果进行分析,研究坡度对阶梯溢流坝掺气水流水深的影响。通过对大坡度溢流坝掺气水流水深的具体研究,能让我们进一步了解影响掺气水深与坡度之间的关系,从而能确定计算掺气水流水深的方法,通过数值模拟的方法寻找出经济实用的大坝坡度,确定溢流坝的边墙高度,防止水流从边墙溢出,进一步提高大坝的安全性。
1 FLOW-3D软件的基本原理和基本方程
1.1 基本控制方程
FLOW-3D的基本方程是根据液体流动连续性方程与纳维-斯托克斯方程,通过对所有网格计算这个两个方程,得到每个小部分的结果,然后得出整体的流动情况。FLOW-3D软件功能很强大,采用数值计算技术先进。通过数据的改变和物理模型的选择使用者可以展现不同的流体运动现象。
(1)连续方程式:
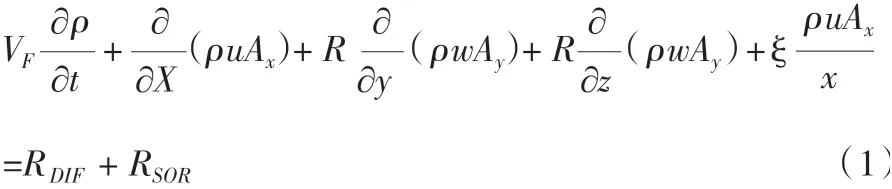
式(1)中可压缩流体要求得到完整的密度输运方程;不可压缩流体中密度是一个常数。式(1)可化为:
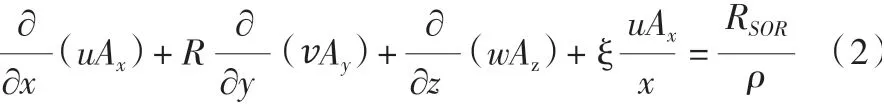
(2)动量方程
将流体流速(u,v,w)在x,y,z三个方向上的运动方程添加到N-S方程上:
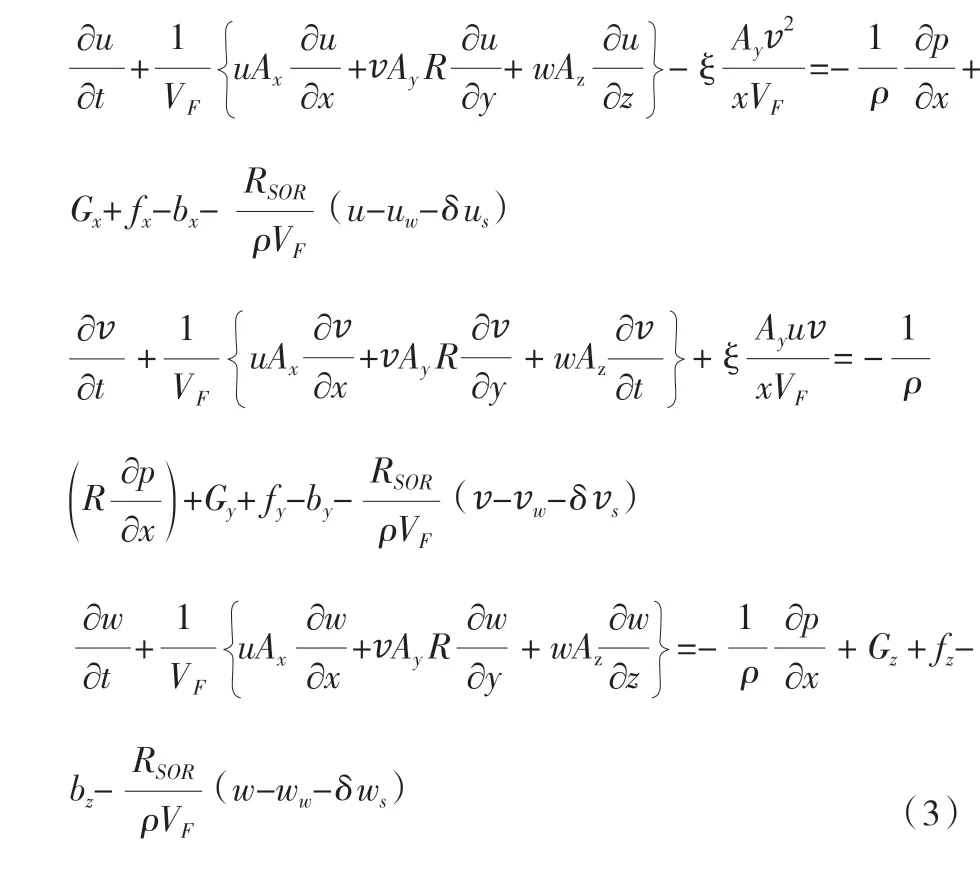
式中:Gx、Gy、Gz分别为流体的加速度在x、y、z三个方向上的数值;bx、by、bz为经过导板或多孔介质的流体损失;fx、fy、fz为粘性加速度。
2 流场数值计算基本思路
本文通过引入中间速度的概念代入差分动量方程中求出其值,然后再将求出的中间速度值代入连续性方程后求出速度场,对比是否与压力场符合,若不符合,则进行修正后接着重复上述步骤,逐渐迭代得出结果。计算示意图见图1。
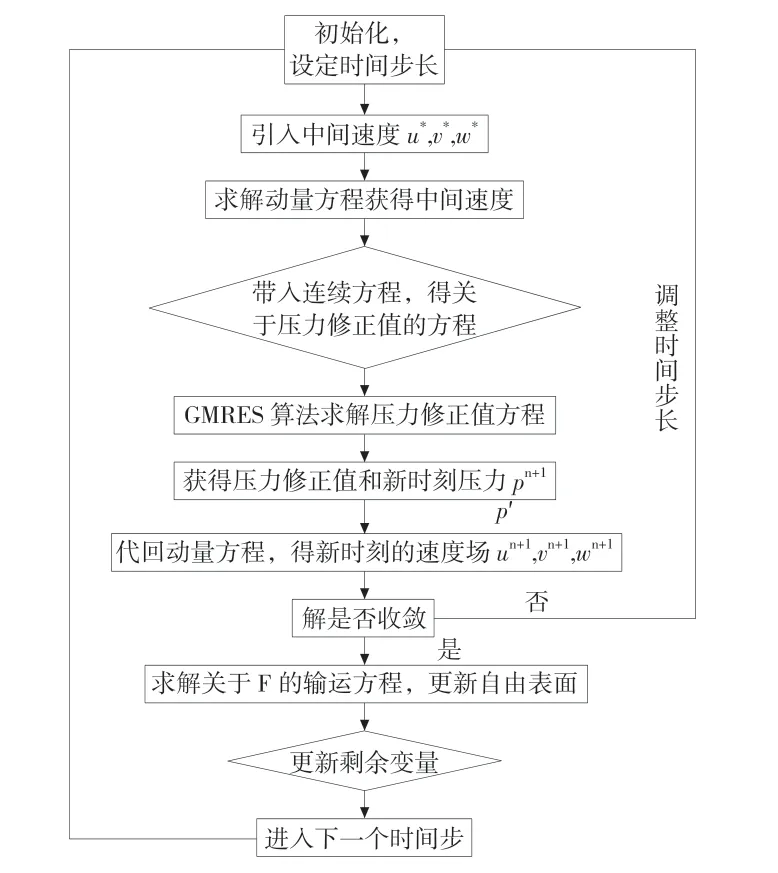
图1 控制方程求解流程图
FLOW-3D使用第一个结构网格的矩形单元,这种方法节约内存的同时还能保持较高的精度。进口边界条件属于第一类,需要对全部的变量给出一个确定的值。通常取速度进口边界为断面进口边界条件,速度通过实验测值确定。对于湍流,由于确定方法较为困难,一般用进口平均流来确定湍流动能;出口边界属于第二类,与进口相比较,此边界较为简单,因为大多数泄水出水口为急流,下流的相关物理参量影响不到上流,因此对下流的边界设定对计算影响很小。
泄水建筑物的固体边界如挡墙、底板、壁面均为壁面边界条件。FLOW-3D中默认所有流体结尾无滑移壁面。要想知道壁面附近流速的具体分布,可以通过在壁面附近生成一个计算面来获取。一般来说,对于模型上表面与空气接触的地方都可以定义为相对气压为0的部分。
3 阶梯溢流坝的结果讨论
3.1 数学模型建立
实验模型由上游坝面、曲线堰、过渡段与阶梯溢流坝构成。模型总高度为102.63 cm,堰上水头为10 cm。进口段的曲线堰采用WES曲线绘制而成,为了使水流平滑过渡到接替段,后面又接了一段短斜坡。实验中台阶的类型一共取三种来分别实验对应的坡度为51.3°、60°与70°。
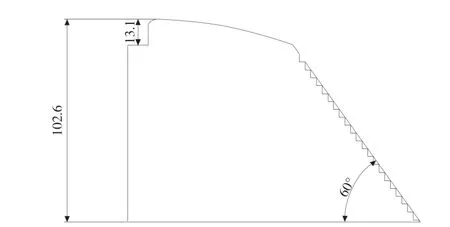
图2 60°阶梯溢流坝模型示意图(单位:cm)
对于3个模型,各设置适宜其坡度尺寸的阶梯尺寸,其样式见图3。

图3 溢流坝阶梯样式(单位:cm)
3.2 网格的划分
本次对于阶梯溢流坝的网格划分采用非均匀网格的划分方式,将阶梯的边缘点设为固定点,这样可以提高对阶梯的分辨率,使得阶梯的棱角不会被模糊掉。网格的划分见图4。
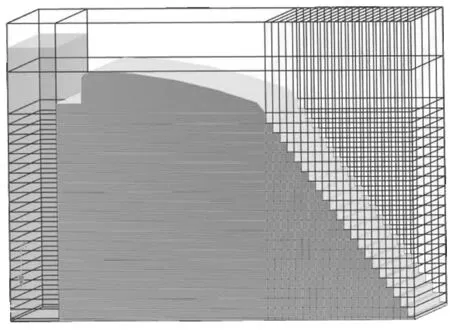
图4 网格的划分
为控制计算的精度和效率,在阶梯处的网格尺寸设置为边长为0.01 cm的立方体,在其他部位的网格设置为边长为0.05 cm的立方体,总体控制下来一共有635431个网格。
3.3 边界条件的设置
对于左右和底面采用墙面边界,进口段采用水深入口条件,已知水深条件。下流出断面采用自由出流条件。自由表面采用相对大气压为0的普通表面。
3.4 成形条件的设置
在模型的物理特性界面中选择重力模型、紊流模型与掺气模型。重力模型中取9.81 N/kg的重力加速度。紊流模型选择上文中常用RNG模型。掺气模型中取默认的掺气系数。
3.5 水流流态
下面以60°阶梯溢流坝为例,5 s内,每隔一秒的整个流动情况见图5。
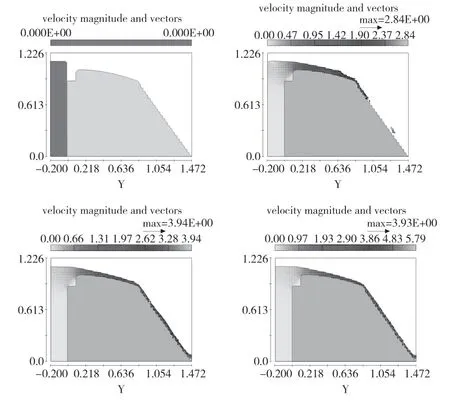
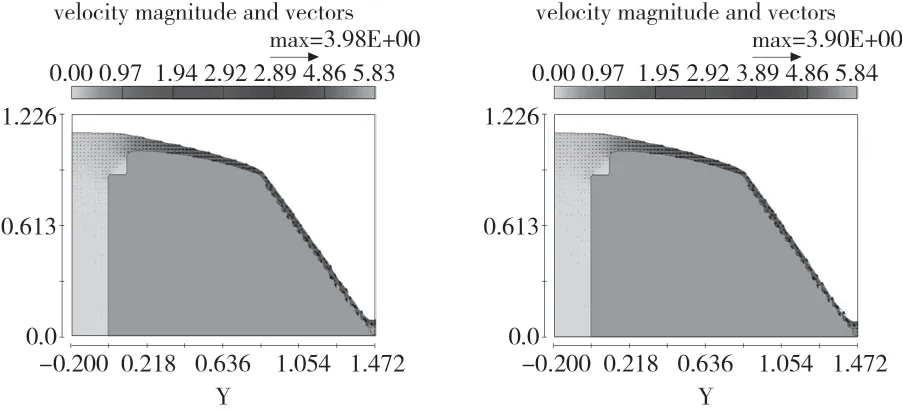
图5 每一秒流动情况图
从图5可以看到,水流平滑地在曲线堰与过渡段上游动过后进入到阶梯段。在阶梯段中,水流分为跌落水流和滑行水流两个部分。下层的水流在阶梯面的突变作用下,在阶梯水平断面、纵向断面与上层水流底面构成地区域内进行漩涡的流动。上层的水流在下层水流漩涡流动构成的虚拟底板上进行滑行流动,在泄流稳定后,水流运动情况与普通光滑的溢流坝几乎相同。水流的水深在下流过程中先是持续缓慢下降,到达掺气稳定的情况后开始保持平稳,直到最后到底部时迅速升高。
3.6 掺气水深
对之前的流态分析图观测可知,在第五秒时,水流已经达到一个稳定的状态了,各模型在第五秒时的掺气浓度分布见图6。
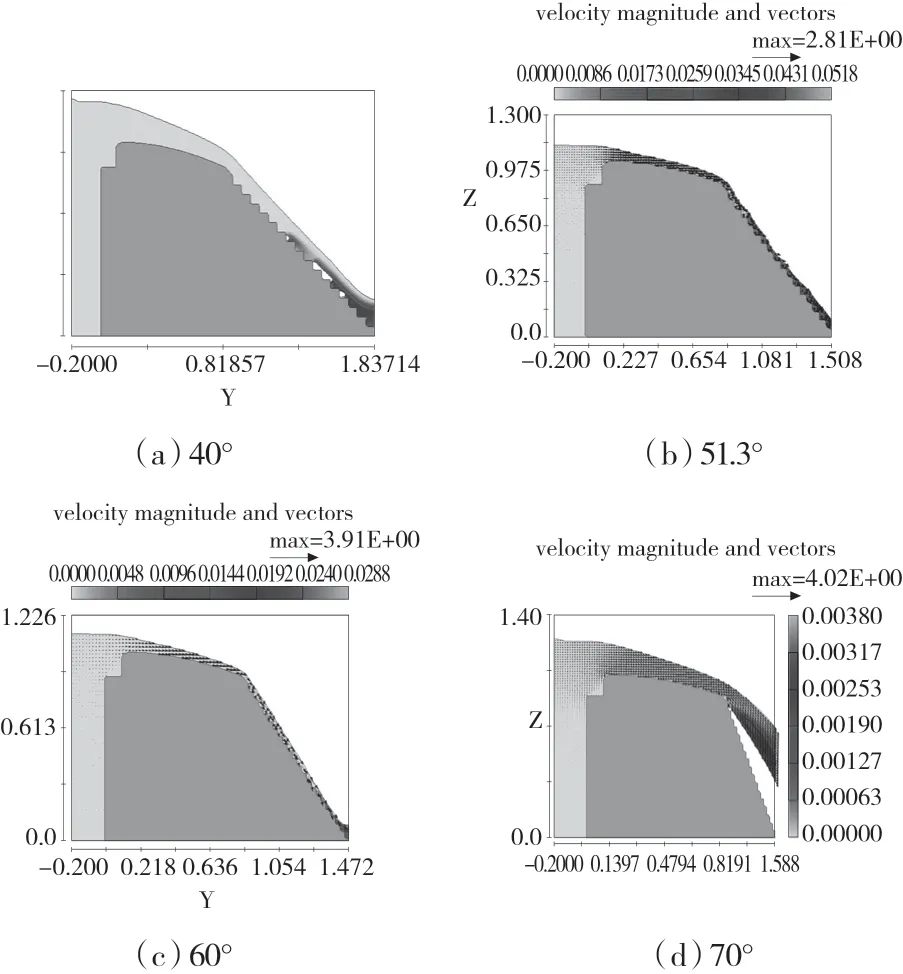
图6 第5秒不同模型掺气浓度分布图
其中,70°时阶梯溢流坝不能正常泄流,将其除外,对其他图中数据进行分析,可以发现,随着坡度的增加,水流到达掺气点的距离也在进一步增加。51.3°时,阶梯溢流坝在0.654 m处便已经开始发生掺气,而在60°时,溢流坝在0.253 m处才发生掺气现象。
下面以51.3°、60°与70°坡度阶梯溢流坝为例,以中间段第10 s时的水深计算结果来分析坡度对掺气水深的影响,见图7。
在排除70°时不能正常泄流的情况后,由图7 结果可以看出,当坡度提升之后,阶梯溢流坝达到掺气稳定点的距离将会变长,同时其稳定后的掺气水深也将会变为更低。当水流到达底部后,坡度更大的阶梯溢流坝水深的提高量更大。具体过程见图8。
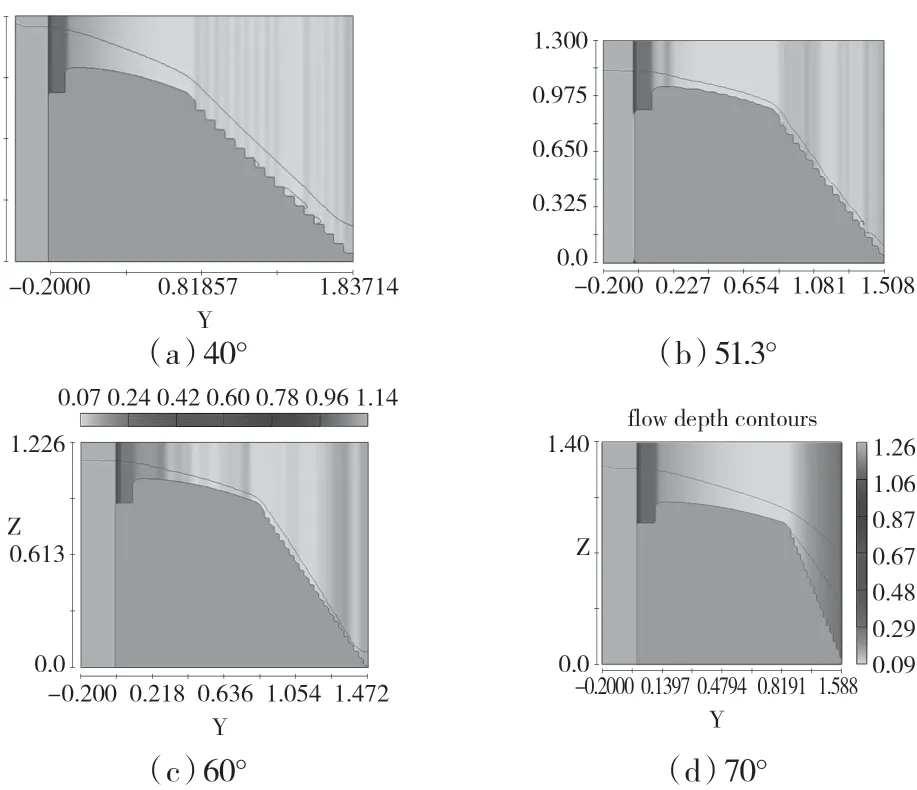
图7 第10s时不同坡度阶梯溢流坝掺气水深计算结果
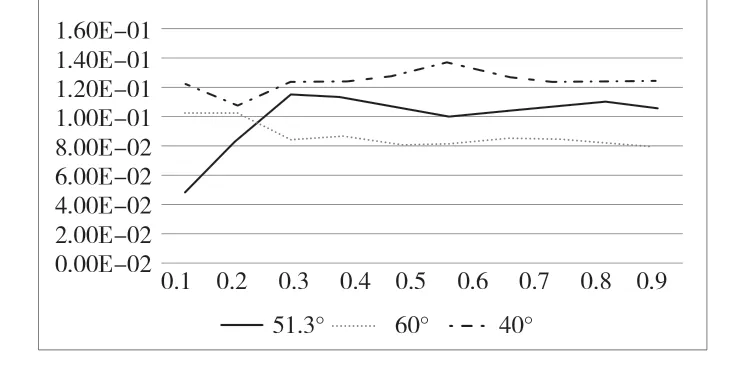
图8 不同坡度下阶梯溢流坝的掺气水深沿程分布图
4 结语
本文利用Flow-3D软件用数值模拟的方法计算了大坡度阶梯溢流坝的掺气水深的相关问题得到如下几个结论:
1)阶梯溢流坝上的掺气水流分为两个部分:跌落水流和滑行水流。下层的水流在阶梯面的突变作用下,形成了一个在阶梯水平断面、纵向断面与上层水流底面构成地区域内进行了漩涡的流动。上层水流在下层水流漩涡流动构成的虚拟底板上进行滑行流动,在泄流稳定后,水流运动情况与普通光滑的溢流坝几乎相同。
2)阶梯溢流坝的水流在运动过程中,沿程掺气水流水深分布情况为:水深在下流过程中先是持续缓慢下降,到达掺气稳定的情况后开始保持平稳,直到最后到达底部时迅速升高。
3)坡度逐渐提高后阶梯溢流坝达到掺气稳定点的距离将会变长,但同时其稳定后的掺气水深也将会变为更低,当水流到达底部后,坡度更大的阶梯溢流坝的水深提高量更大。

