基于偏序集的苏锡常地裂缝危险性评价研究

黄 亮

四川文理学院 体育学院, 四川 达州 635000

1 引言

地裂缝是一种在人为活动或自然作用下, 地表岩土体发生开裂形成呈带状分布的裂缝的地质灾害现象。 地裂缝具有隐藏性、 随机性、 发育性等特征, 破坏城市建筑、 交通管道、 生命线工程作业等, 给城市建设带来了巨大损失, 同时在耦合效应下会进一步触发一系列环境问题[1-4]。 因此, 准确地判别地裂缝发育程度, 古地裂缝稳定与否, 地裂缝扩展速度不再加剧, 是地裂缝预防与防治的首要问题, 而科学地、 系统地进行地裂缝危险性评价对于提高城市建设经济效益具有重要的社会价值与现实意义。

目前, 国内许多学者在地裂缝危险性评价领域进行了深入研究, 其方法主要体现在5 个部分: (1) 应用模糊综合评价方法。 如郭晋艳[5]等结合层次分析法确定权重, 建立地裂缝危险性模糊综合评价模型。(2) 应用统计学理论。 如王卓、 许强等人[6]运用统计分类与聚类分析两方法, 对地裂缝等级进行评价分级。 (3) 应用支持向量机数学算法。 如袁颖等[7]结合主成分分析法, 引入支持向量机建立地裂缝危险性预测模型。 (4) 应用灰色关联度理论。 如方东等[8]基于灰色关联度理论, 计算关联度与权重, 对地裂缝进行危险性分区。 (5) 神经网络分析。 如朱锦旗、 陈佩佩等[9][10]利用改进的神经网络对地裂缝危险性进行分类。

基于以上方法可以分成两种评价方式, 即类别贴近度模型和样本自学习模型。 方法(1) 属于类别贴近度模型, 即应用多种权重确定方法, 依据最大隶属度进行综合评判。 该模型专家经验得到充分发挥, 但过于主观, 客观数据本身所附有的信息得不到体现。此外, 选择赋权方法多样, 存在争议问题。 方法(2)- (5) 属于样本自学习模型, 即应用数学算法进行训练样本自学习, 以达到期望值。 该模型适用性较好,但过于客观, 忽视专家经验, 可信度不佳, 同时依赖足够样本量, 样本不足无法进行可靠的数学算法。 鉴于以上两种评价方式的优缺点, 拟将蕴含权重信息的偏序集引入地裂缝危险性评价研究中, 提出一种新的地裂缝危险性评价方法。 解决赋权争议问题同时兼顾主客观问题, 并利用层集信息判别地裂缝危险程度,为地裂缝预防与防治提供新思路。 同时, 依据地裂缝危险性排序, 在不影响安全作业的前提下, 又能科学合理地选择高危地裂缝进行及时分析处理。

2 地裂缝危险性评价标准的建立

2.1 评价指标选取

科学合理的选取评价指标直接决定评价结果是否准确、 可行。 不同学者研究领域不同, 其理论方法运用也不同, 选取不同的评价指标对地裂缝危险性展开评价。 鉴于前人研究成果, 本文选择以下6 个指标(分别用X1、X2、X3、X4、X5、X6表示):

(1) 基岩埋深X1。 取基岩所处地面以下埋深值。

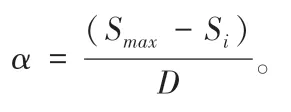
(3) 第Ⅱ承压含水层厚度X3。 基于实际, 地下水开采主要为第Ⅱ承压含水层。 第四纪沉积层厚度存在差异, 过度开采地下水会导致岩层发生不均匀沉降现象, 进而加快地裂缝破裂。

(4) 黏性土层厚度X4。 地面沉降发生其主要影响因素之一为黏性土层。 研究区内第四纪沉积层以砂层和粉质黏土为主。 黏性土层厚度越大, 其发生地面沉降的可能性越大。

(5) 主采层水位埋深X5。 大量开采地下水, 主采层水位埋深增加, 含水层失水, 水头压力减弱, 有效应力增加, 失水含水层被迫压缩, 进而不均匀沉降,其沉降量随主采层水位埋深的增加而增加。

(6) 地面沉降梯度X6。 取两地裂缝主线处地面沉降量差值与其水平距离的比值。 其计算公式:(D2-D1)/L。

2.2 地裂缝危险性划分标准

地裂缝评价指标的危险性分级没有统一标准, 不同研究区其划分标准是不一的。 基于苏锡常地裂缝数据(见表1), 结合文献[8]划分标准, 本文对指标X1、X2、X3、X4、X5、X6采用实测数据评价, 同时将地裂缝危险性评价等级划分为极度危险、 高度危险、中度危险、 轻度危险, 4 个危险等级分别用I、 II、III、 IV 表示, 详见表2。

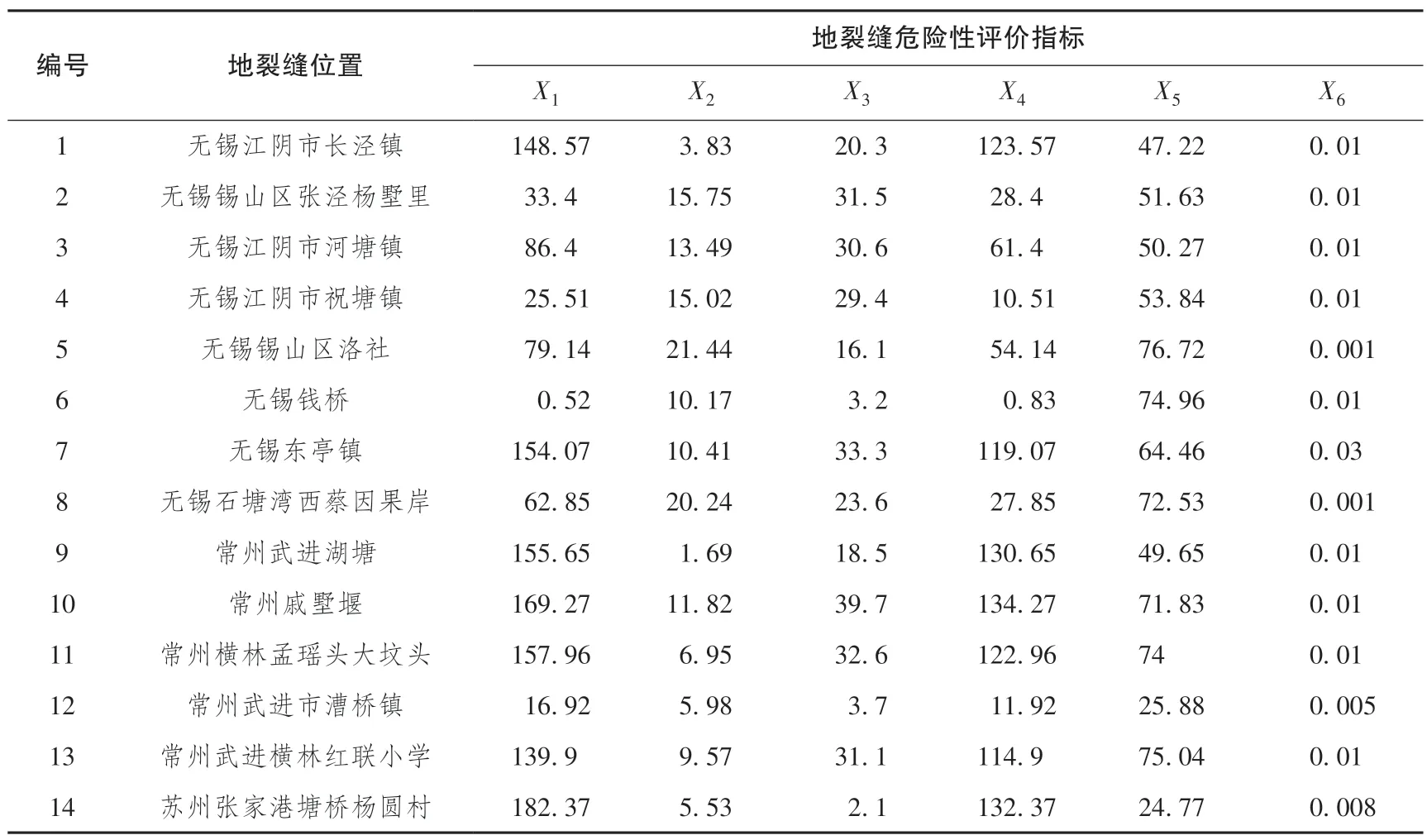
表1 苏锡常地裂缝原始数据Table 1 Original data of Su Xi Chang ground fissure

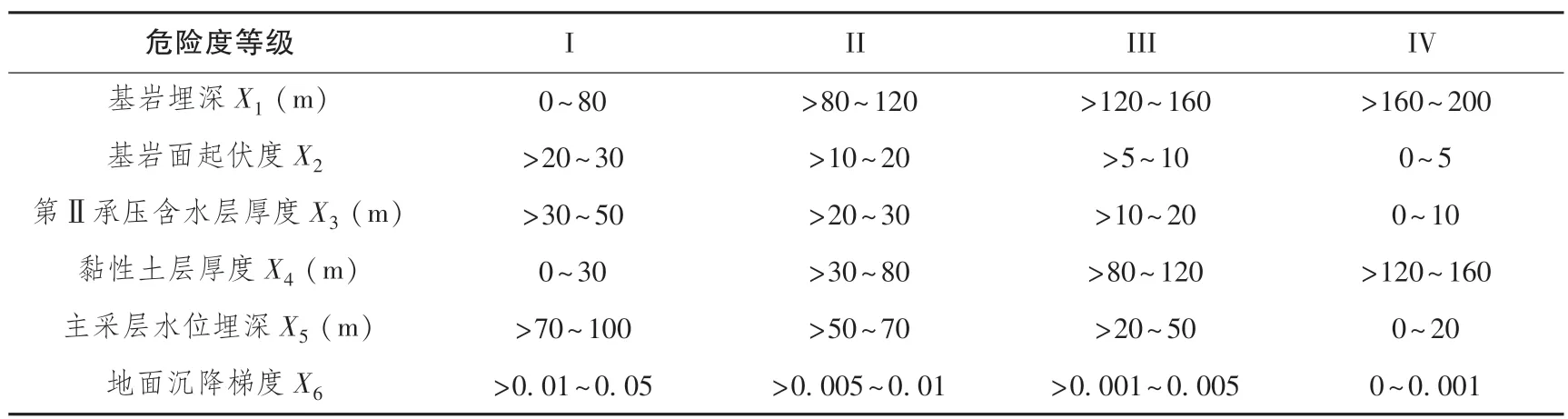
表2 苏锡常地裂缝危险性评价标准Table 2 Su Xi Chang ground fissure risk evaluation criteria

3 地裂缝危险性的偏序集评价模型

3.1 偏序集理论与评价模型

给定评价模型O = I,N,H, 评估关系模型U =(I,R) , 其中I= {i1,i2,…,im} 为评估对象或方案集;N= {b1,b2,…,bn}为评价准则集;H= {hk:I→Vk| k =1, 2,.. m} 为方案集与评价准则之间的关系集;R为方案集之间的关系集,R表示xi与xj的一个二元关系, 且R满足:

(1) 自反性: 对任意x∈I, 有xRx;

(2) 反对称性: 对任意x,y∈I, 若xRy且yRx, 则x = y;

(3) 传递性: 对任意x,y,z∈I, 若xRy且yRz, 则xRz, 称R为I上的偏序关系[11]。

对于含有m个样本n个指标的决策问题, 文献[12]根据各准则权重秩次w1≥w2≥…≥wn, 用矩阵形式表示蕴含权重信息的方案决策问题:

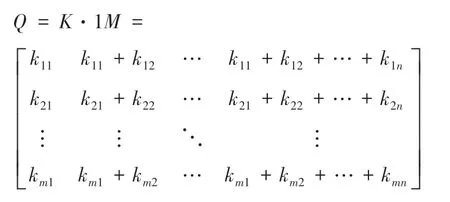
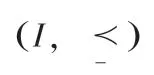
HR=(R - E)-(R - E)*(R - E)

其中,R为关系矩阵,HR为Hasse 矩阵,E为单位矩阵,*为布尔运算。

再由Hasse 矩阵绘制Hasse 图, 通过Hasse 表现的层集信息判断地裂缝危险程度。

最后, 引入上、 下集概念, 应用Brüggemann[14]提出的上下集公式, 对各个地裂缝进行高度值计算。其公式如下:

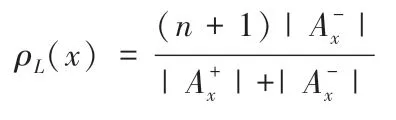
3.2 评价步骤[15]

(1) 确定评价指标集;

(2) 指标数据无量纲化处理;

(3) 获取指标权重排序信息;

(4) 通过计算得出Hasse 矩阵;

(5) 绘制Hasse 图及结果分析, 对方案进行分类和排序。

4 应用实例

苏锡常地区是长江三角洲经济区最发达、 城市工业程度较高的地区之一。 该地区经济发展的同时, 也带来了巨大的环境影响。 随着城市化发展加速, 地下水严重开采, 现已出现25 条地裂缝, 主要分布于常州武进、 江阴、 无锡及张家港等地级市, 横穿城市建筑、 交通管道、 生命线工程等, 给城市建设造成了巨大的经济损失。

4.1 数据处理

偏序集决策是通过评价准则建立偏序关系进而选择最优方案的一种多准则决策分析方法, 依据其理论原理构造“等级标准训练样本”, 以区分各层集间的优劣标准, 保证更为准确的分级评价。 本文采用等间距内插值法, 即是等级标准等间距插值。 考虑原始数据的信息获取是通过实际野外调查与前人资料综合分析下所得到的, 故等间距内插的样本也是符合该研究区地裂缝特点。 对地裂缝I 级危险等级, 指标X1插值: 指标X1在0～80 范围内属于I 级危险区, 将0～80区间划分为等间距的四等分, 即所插值的点为20、40、 60; 加上左端点值0, (值得注意的是右端点值80为指标X1在80～120 范围内的左端点取值, 以避免两个等级取值的信息重合) 共计4 个I 级标准样本点; 同理指标X1在80～120 区间的样本点分别为80、 90、 100、110 共计4 个II 级标准样本点; 在120～160 区间的样本点分别为120、 130、 140、 150 共计4 个III 级标准样本点; 在160～200 区间的样本点分别为160、 170、 180、190、 200 共计5 个IV 级标准样本点。 同理其余各指标插值可获得“等级标准训练样本”。

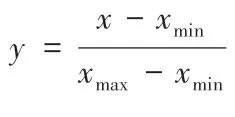
4.2 指标权重排序

偏序集评价结果的准确性取决于指标权重秩次。目前, 主观赋权法与客观赋权法是获取权重值主要的两种计算方式。 通常情况下, 主观赋权法依托专家经验具有主观强而精确不足, 而客观赋权法依靠数据说话更加客观可信。 然而, 相关研究显示, 客观赋权法赋权及应用过程为“从内部来到内部去”, 信息较单一, 同时受样本变化的影响, 其评价结果不稳定。 与客观赋权法相比, 主观赋权法依据丰富的专家经验,把握“质” 的信息与工程实际结合, 在复杂多因素环境下, 充分发挥专家优势, 分析外部相关环境, 得出的结果更为可信。 基于此, 本文引入偏序集理论到地裂缝危险性评价研究中, 只需获取权重排序, 而不拘泥于具体大小值。 权重排序由文献[4]获取, 依次为X6、X5、X1、X2、X4、X3。

4.3 Hasse 矩阵

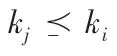
4.4 Hasse 图

通过Hasse 矩阵绘制Hasse 图(见图1), Hasse图与Hasse 矩阵一一对应, 是有向图的“精简” 版,即对给定的比较关系有向图, 保留两点之间最大路径, 删除之外的非最大路径, 得到“剩余” 的图为Hasse 图。

从图1 可以直观的获取各样本危险性分级及聚类信息。 偏序集方法原理最大优势是上集优于下集(如A3指向A2, 表示A3优于A2), 且具有传递性。 因此,在图1 中, 越是位于图上端的节点群体, 表示的地裂缝危险性越小, 根据构造的“等级标准训练样本” 可以将31 个样本从上往下依次划分为4 个危险层集群:

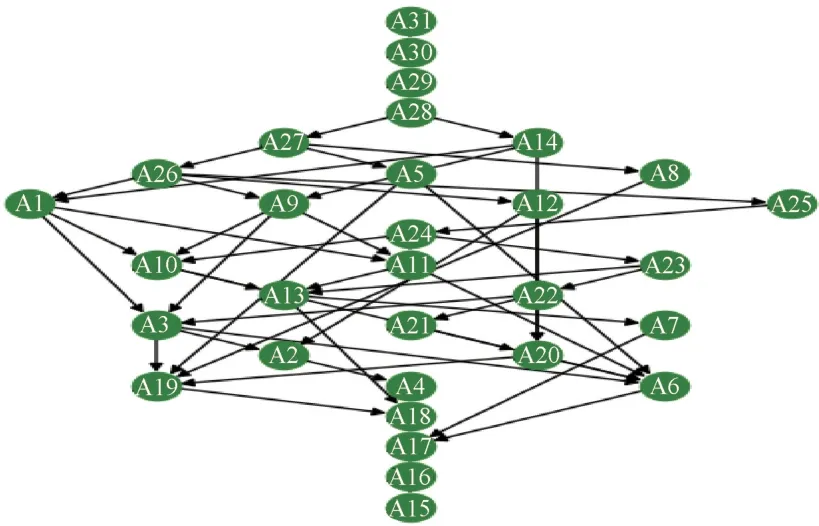
图1 地裂缝危险性Hasse 图Fig.1 Hasse diagram of ground fissure risk

(1) IV 级层集群(轻度危险): 27、 28、 29、 30、31、 14;

(2) III 级层集群(中度危险): 23、 24、 25、 26、10、 11、 1、 9、 12、 5、 8;

(3) II 级层集群(高度危险): 19、 20、 21、 22、4、 6、 2、 3 、 7 、 13;

(4) I 级层集群(极度危险): 15、 16、 17、 18。

具体表述为: 在31 个样本中, 样本15 ～31 是按照偏序集理论优势人为构造的虚拟样本, 根据图1 可知, 样本28、 29、 30、 31 各自为一层, 样本14 与虚拟样本27 处于同一层集, 样本14 与虚拟样本27、28、 29、 30、 31 组成IV 级层集群, 表示各样本对应的地裂缝危险程度为轻度危险; 同理可以判断出, 样本10、 11、 1、 9、 12、 5、 8 与23、 24、 25、 26 组成III 级层集群, 表示各样本对应的地裂缝危险程度为中度危险; 样本 4、 6、 2、 3 、 7 、 13 与19、 20、 21、22 组成II 级层集群, 表示各样本对应的地裂缝危险程度为高度危险; 样本15、 16、 17、 18 组成I 级层集群, 表示各样本对应的地裂缝危险程度为极度危险。

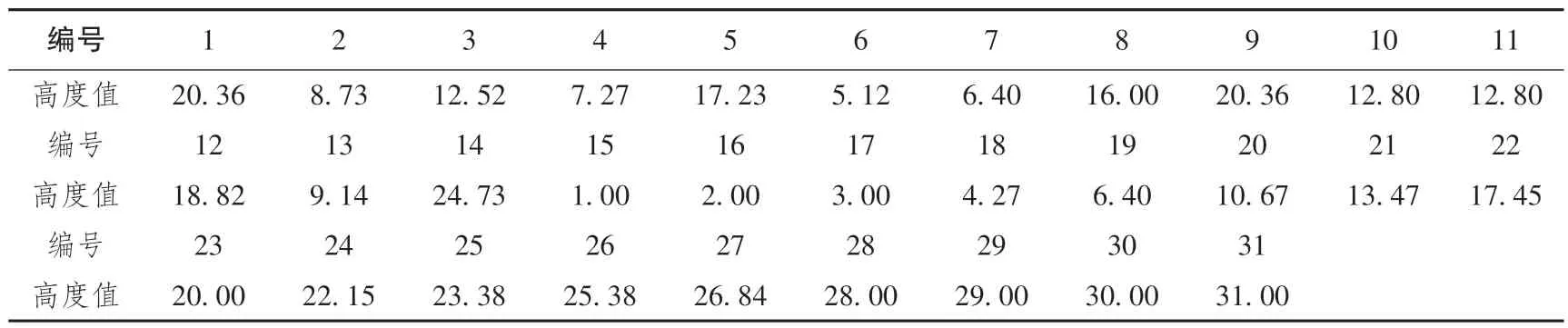
表3 各地裂缝高度值计算结果Table 3 Calculation results of crack height values in different places

地裂缝危险性最大的为6 号, 这与其实际现状(无锡钱桥地区大量开采地下水, 地下水埋深高达70 m, 加之基岩埋深较浅, 岩体起伏度较大, 一旦岩体碎裂, 地面沉降梯度将增大, 进而加剧破裂扩展, 周边影响范围扩大) 是一致的; 采空区危险性最小的为14 号, 该地裂缝实际现状(苏州张家港塘桥杨圆村地下水开采程度最小, 地下水埋深为24 m 左右, 基岩埋深较大, 高达180 m, 岩体起伏度较小, 加之可供开采的第II 承压含水层厚度很小而黏性土层居多, 故地面沉降影响是很小的) 也是一致的。 实际上, 同时处理大量的地裂缝问题时, 在时间和人力上是不现实的, 现根据地裂缝危险性排序, 能科学合理地选择处理高危地裂缝, 为地裂缝预防与治理提供科学指导,这将有利于相关部门制定相应的防治措施。

4.5 结果分析

由表4 可以看出, 本文方法所得到的分析结果与文献[8]运用灰色理论所得到的分析结果是一致的,只是危险性等级命名有所差异, 同时本文方法与文献相比有三方面独特之处:

表4 本文方法判别结果与其他方法判别结果比较Table 4 The discriminant results of this method are compared with those of other methods

(1) 偏序集决策法只需获取权重排序, 而非具体权重数值, 解决了赋权争议问题, 同时操作更为简单, 避免了精确赋值的困扰。 事实上, 多数权重计算方法所得到出权重排序是基本一致, 只要赋权方法是有效的, 权重排序就能推广应用。 同时在解决复杂多因素、 信息模糊不全决策问题方面, 可以依据专家经验获取权重排序, 从而解决因无具体权重值而不能应用的模型问题。

(2) 样本分层信息明显。 通过Hasse 图能直观地获取层次信息, 可以观察到本文31 个样本分成了4 个等级群, 且从上往下看第IV 等级群优于第III 等级群,第III 等级群优于第II 等级群, 第II 等级群优于第I等级群, 即:

{A31,A30,A29,A28,A27,A14} ≻ {A26, A25,A24, A23, A10, A11, A1, A9, A12, A5, A8}

≻{A22,A21,A20,A19,A4,A6,A2,A3,A7,A13} ≻{A18,A17,A16,A15}

(3) 模型识别排序具有很好的鲁棒性。 如方案A1优于方案A10, 方案A10优于方案A13, 方案A13优于方案A6等可比关系, 只要权重排序不变动, 则偏序结构就不变, 防止了权重仿真过程发生。

5 结论

应用偏序集理论对地裂缝危险性展开评价, 解决了赋权争议问题, 提出了一种更为稳健的评价方法:

1) 本质上, 应用偏序集其优势在于用一个权重空间代替权重向量, 而权重空间只需通过专家定性分析即可获取, 即是权重排序。 同时蕴含权重信息的偏序集是无数个权重合成的结果, 相比其他方法更为简单、 稳健。

2) 本文方法可以扩展其线性模型, 只要其赋权方法能有效获取权重排序信息, 其他地区地裂缝危险性评价方法均可用偏序集表示。

3) 本文方法能直观地突显分层聚类及排序信息,有利于应急管理部门准确判别地裂缝危险程度, 并及时处理, 可有效预防地裂缝进一步破裂扩展, 防止出现更大的经济损失。