基于流固耦合作用的抽水引起地裂缝活动量计算模型

刘 超, 郭乐凡, 袁 颖, 周爱红, 刘雪弟

1. 河北地质大学 城市地质与工程学院, 河北 石家庄 050031; 2. 河北省高校生态环境地质应用技术研发中心, 河北 石家庄 050031; 3. 河北省地下人工环境智慧开发与管控技术创新中心, 河北 石家庄 050031

0 引言

地裂缝是指地表岩土体在自然或人为因素作用下产生开裂, 并且在地表形成具有一定宽度和长度的裂缝, 在人类活动地区, 地裂缝已经成为了一种地质灾害。 地裂缝在世界各地均有不同程度的发生, 在中国地裂缝主要分布在大华北地区[1]。 2005—2013 年期间, 中国地质调查局水文地质环境地质调查中心对保定市、 沧州市、 石家庄市、 衡水市、 廊坊市、 邢台市、 邯郸市、 唐山市、 秦皇岛市9 个地区进行了地裂缝灾害专项调查, 共调查发现有地裂缝839 条[2]。 地裂缝对农田、 公路、 桥梁、 隧道、 水利设施等建(构) 筑物造成了严重的破坏, 对人类的生产生活、工程建设造成了巨大的经济损失, 同时也在一定程度上引起了社会心里恐慌。

人为过量开采地下深层承压水是导致地裂缝活动的重要原因, 开采地下水引起了地裂缝两侧地面差异沉降, 进而诱发了地裂缝的活动[3-6]。 地裂缝活动主要表现为裂缝上下两盘在竖直方向上的错动[7-9], 据此预测地裂缝的活动量, 能够为建筑物跨地裂缝防灾设计提供科学依据。 地裂缝错断了含水层, 影响了孔隙水压力的分布和各含水层之间的水力联系, 同时也改变了土体变形的边界条件, 因此, 开采地下水引起地裂缝活动是一个复杂的物理力学过程。 涉及了地下水渗流场、 土层变形场, 以及地裂缝边界条件等众多因素相互作用的影响。 抽水引起变形的计算方法包括“两步走”、 部分耦合和完全耦合三大类方法。 “两步走” 方法首先计算渗流, 根据计算得到的渗流场再计算土体变形, 计算渗流和变形是两个独立的过程, 采用不同的计算方法, 在计算过程中, 渗流和变形的计算参数保持不变[10-11]。 “两步走” 的方法操作简单,但实际地层中, 水与土是互相影响的, 渗流对土产生了渗透力, 导致了土体变形, 反之土体变形也会引起孔压改变, 土体中的孔压与变形是不断变化的。 部分耦合的思想是在两步走的基础上, 将计算参数设置为可变的[12], 渗流和变形仍然是分开计算。 完全耦合则是真正的三维耦合, Biot 提出了渗流场与变形场的完全耦合模型[13], 此后, 还有一些学者根据不同条件建立了完全耦合模型[14-15]。 完全耦合模型更符合物理机制, 但其求解复杂, 多采用数值方法求解[16-17], 以Biot 固结理论为基础, 采用完全耦合方法, 计算差异沉降量作为地裂缝活动量是一种合理的思路。

本文考虑开采承压水引起地裂缝的机制, 基于理想的地层模型, 利用FLAC3D6.0 软件平台编写代码,建立地下水渗流场与变形场三维流固耦合数值计算模型, 模拟渗流场、 变形场以及地裂缝活动的发展过程, 同时对比承压含水层厚度的差异对地裂缝活动的影响, 为研究地下水渗流与土体变形耦合本构关系以及预测地裂缝活动量奠定基础。

1 流固耦合基本理论

采用FLAC3D6.0 进行流固耦合计算时, 基于单元体平衡微分方程、 流量平衡方程、 本构方程等, 建立孔压、 流量等与土体应力应变之间的关系。

在土层中取一微单元体, 单元体满足平衡微分方程,· 为速度分量,t为时间。

式(1) 中, 土体的密度包括固体颗粒和孔隙水两部分, 即

ρ =(1- n)ρs+ nρw(2)

式中,ρs为固相密度,ρw为液相密度,n为孔隙率。水的渗流满足达西定律

式中,ρ为密度,σij为应力分量,ui

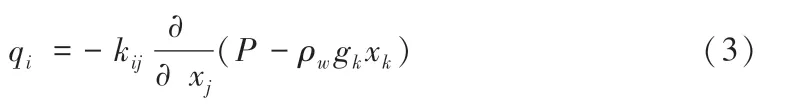
式中,qi为流量,kij为渗透系数,ρw为水的密度。

单位体积内, 水流量平衡满足

式中, ζ 为水的体积变化量,qv为补给源流量。

流固耦合的求解计算中, 节点上流量变化会导致孔压变化, 节点孔压应满足

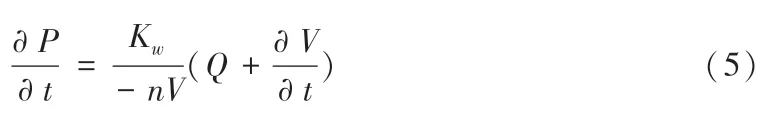
式中,P为孔压,Kw为流体体积模量,V为总体积,Q为节点总流量。

土体的本构关系满足

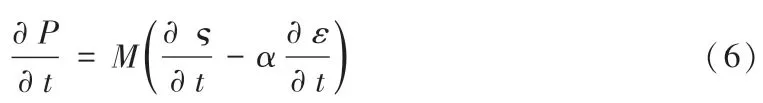
式中,ε为体积应变,α为比奥系数,M为比奥模量。

土体变形满足相容方程

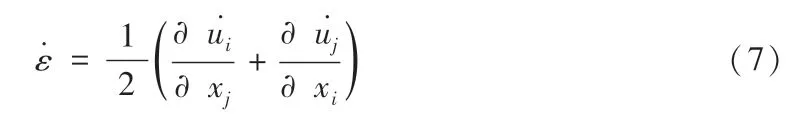
式中,ε应变率分量,α为速度分量。

2 计算模型

选取计算模型, 建立抽水引起地裂缝活动计算模型, 如图1 所示。 以模型底面中点为坐标原点建立坐标系, 地裂缝倾角约80°, 模型中地裂缝上盘包括三个地层, 两个隔水层和一个承压含水层, 承压含水层选取了两种不同的厚度, 隔水层为粉质黏土, 含水层为砂土, 地裂缝下盘为粉质黏土隔水层。 抽水井为完整井, 抽取承压含水层中的承压水。 土体本构模型取为各向同性的弹性模型。 模型参数见表1。

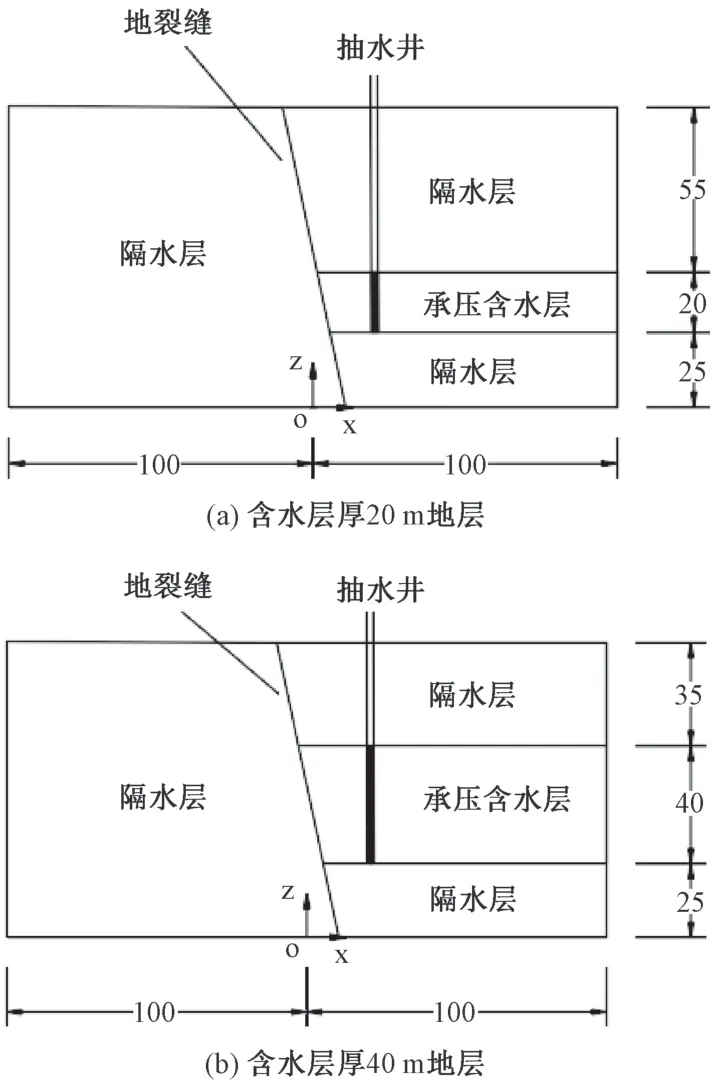
图1 模型地层图Fig.1 Model stratum

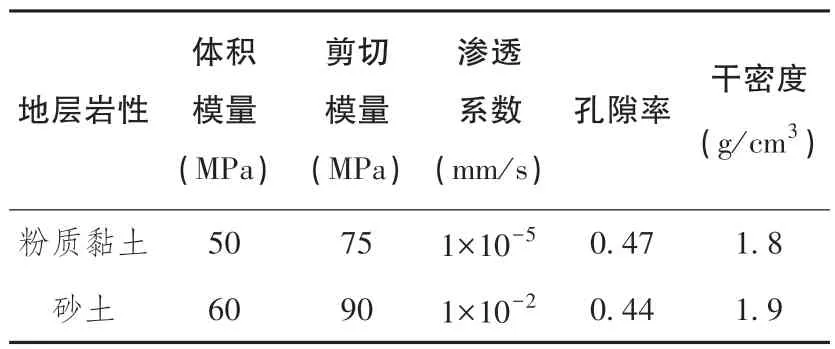
表1 模型参数表Table 1 Model parameters

利用FLAC3D6.0 编写代码建立计算模型, 如图2所示。

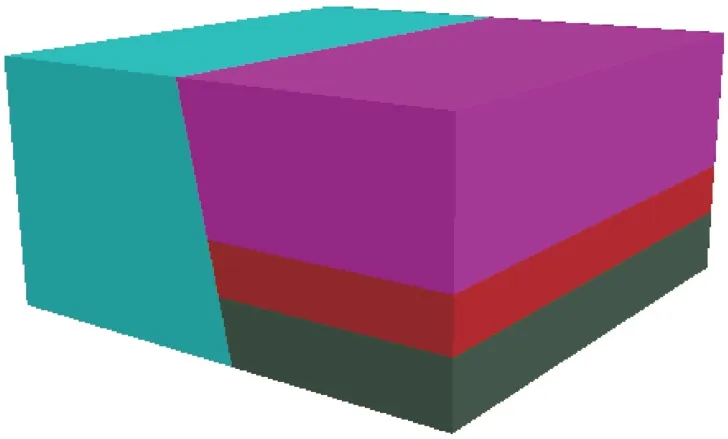
图2 FLAC3D 计算模型Fig.2 FLAC3D modol

模型四周为定水头边界, 底面为隔水边界, 力学模型中, 上边界为自由边界, 四周边界限制水平位移, 底面限制竖直方向位移。 模型首先生成初始应力场和孔压场, 抽水井设置在水平坐标为20 m 处, 抽水量400 cm3/s, 见图1。 地裂缝错断了含水层, 将其考虑为隔水边界, 设置了不透水的结构面单元。 计算方法选取了完全流固耦合方法, 为了反映含水层与隔水层渗透性的差异, 设置含水层的渗透系数远大于隔水层, 同时在承压含水层与隔水层之间设置了不透水的结构面单元。

3 计算结果及分析

计算模拟的结果分别考虑隔水层顶面孔压变化、地表面变形、 以及竖直方向上变形。

3.1 孔压分布分析

在承压层含水层顶面, 孔压随水平位置的变化,如图3 所示。

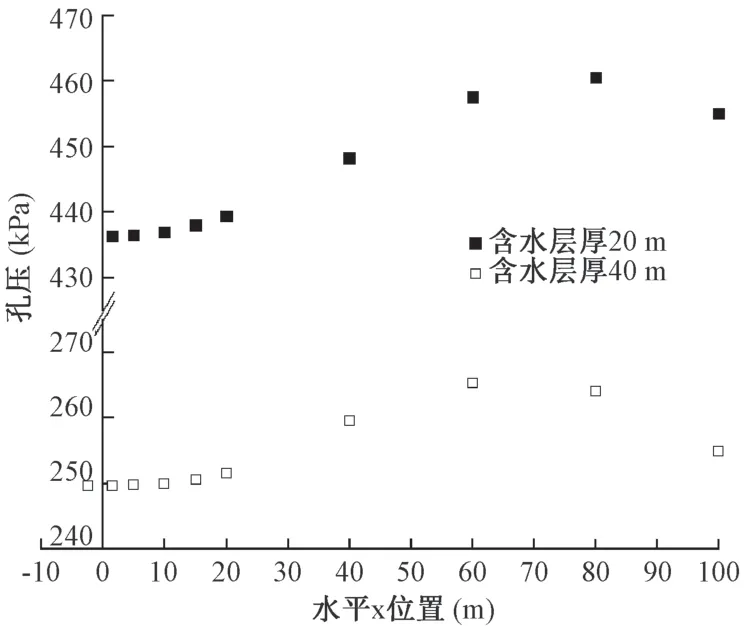
图3 承压含水层顶面孔压分布Fig.3 Pore water pressure at the top of confined aquifer

图3 表明, 地裂缝上盘承压含水层中, 抽水引起了孔压的降落, 由于地裂缝处为隔水边界, 影响了沉降漏斗的形成, 沉降中心并没有出现在抽水井附近,孔压最低处出现在地裂缝附近, 孔压降落最大, 向上盘远处孔压降落逐渐减小, 至恢复到天然状态, 曲线呈上凹形, 从地裂缝向上盘远处, 孔压降落减小的速率由小变大, 再逐渐变小。 变化趋势由抽水井与地裂缝之间的位置关系决定。 含水层厚度为20 m 时, 地裂缝附近的孔压约为436.3 kPa, 含水层厚度为40 m时, 地裂缝附近的孔压约为249.6 kPa。 含水层厚度不同, 含水层顶面标高不同, 抽水井与地裂缝之间的距离也不同, 引起了孔压变化数值上的差异, 孔压的变化的总体趋势基本相同。

3.2 变形分析

3.2.1 地表竖直方向沉降分析

图4 表明, 地裂缝的上盘, 抽水引起了地面沉降, 地裂缝下盘相对静止, 两盘之间差异沉降引起了地裂缝活动。

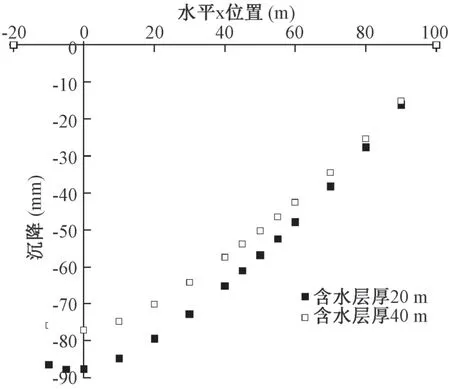
图4 地表面竖直方向沉降Fig.4 Vertical subsidence of ground surface

在地裂缝上盘距离地裂缝越近地面沉降量越大,距地裂缝越远沉降量越小。 沉降变化速率由地裂缝向远处逐渐增加。 地裂缝附近, 含水层厚度20 m 时,地裂缝活动量约为86 mm, 含水层厚度40 m 时, 地裂缝活动量约为75 mm, 承压含水层厚度增加减小了地裂缝活动量。

3.2.2 地表水平方向变形分析

图5 为地表土体水平方向的位移变化, 曲线显示, 地裂缝的上盘, 在距地裂缝约25 m 的范围内,土体背离地裂缝方向运动, 且距离地裂缝越远位移量越小, 含水层厚度为20 m 时, 地裂缝附近水平最大位移量约为14 mm, 含水层厚度为40 m 时, 地裂缝附近水平最大位移量约为12 mm。

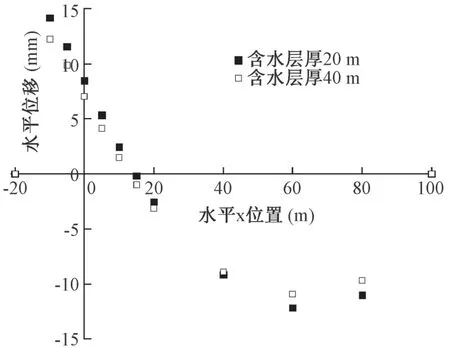
图5 地表水平x 方向位移Fig.5 Horizontal x direction displacement of ground surface

在距地裂缝约25 m 以外, 土体向着地裂缝方向运动, 且随着距地裂缝距离的增加位移量先增大, 在距地裂缝约70 m 处达到位移量最大, 含水层厚度为20 m 时, 最大位移量约为12 mm, 含水层厚度为40 m时, 最大位移量约为10 mm。 随着距地裂缝距离再增加, 位移量逐渐减小, 直至恢复天然状态。

3.2.3 竖直方向变形分析

图6 和图7 为水平位置坐标30 m 处, 竖直方向位移变化, 在承压含水层内, 随着深度增加, 沉降量逐渐减小, 承压含水层顶部沉降量最大。 抽水量400 cm3/s 时, 厚度20 m 含水层顶面最大沉降量约为51 mm, 层厚40 m 含水层顶面最大沉降量约为52 mm。

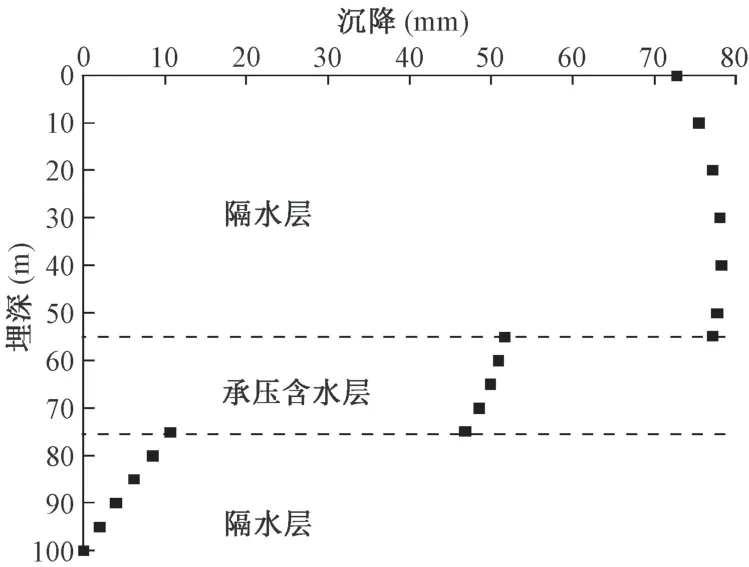
图6 含水层厚度20 m 时竖直方向沉降Fig.6 Vertical settlement of 20 m thick aquifer

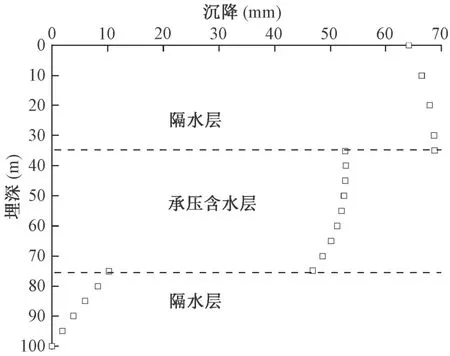
图7 含水层厚度40 m 时竖直方向沉降Fig.7 Vertical settlement of 40 m thick aquifer

在承压含水层上部的隔水层中, 含水层厚度为20 m 时, 地表沉降量约为72 mm, 随深度增加, 沉降量逐渐增大, 在约深40 m 处达到最大78 mm, 而后略减小。 含水层厚度为40 m 时, 地表沉降量约为64 mm, 随深度增加, 沉降量逐渐增大, 在隔水层底部达最大68 mm。 承压含水层下部的隔水层中, 随深度增加, 沉降量逐渐减小, 最大沉降量出现在隔水层上部。

总沉降量上部隔水层大于承压含水层, 承压含水层下部的隔水层最小。

4 讨论

4.1 与理论公式对比分析

式(8) 为直线隔水边界的稳定井流公式, 根据镜像法原理将地裂缝隔水边界等效为虚井, 叠加求解

式中,s为水位降深,Q为抽水井的流量,T为导水系数,r1、r2分别为观测井到虚井和实井的距离,R为影响半径。

以厚度为20 m 含水层为例, 采用隔水边界的理论公式计算的承压含水层顶面的孔压分布, 并与FLAC3D6.0 流固耦合方法计算的结果进行对比, 如图8 所示。

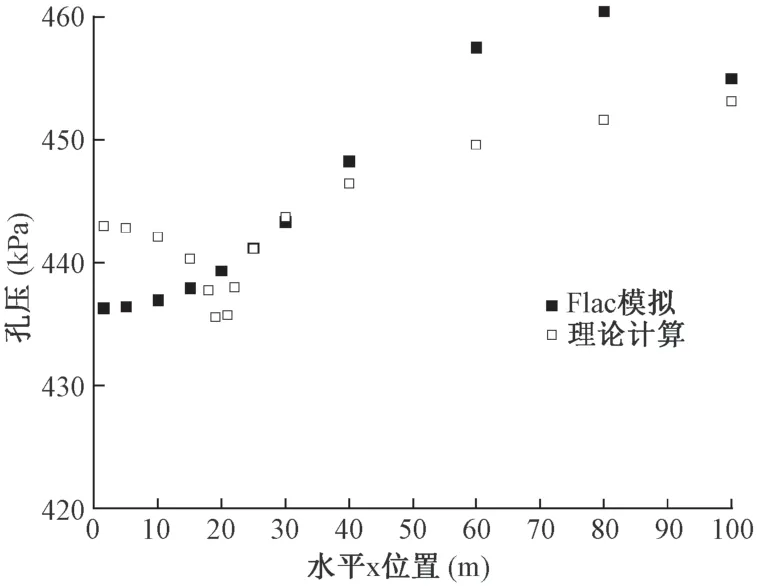
图8 与理论公式对比Fig.8 Comparison with theoretical formula

对比FLAC3D6.0 流固耦合方法和理论公式计算的结果, 孔压的分布形式上略有差异, 理论公式是基于虚井和实井叠加的方法计算, 结果表明, 孔压的分布形成了降落漏斗, 漏斗最低处在抽水井处。FLAC3D6.0 基于流固耦合方法, 孔压除了受到渗流影响, 还受到土体变形的影响, FLAC3D6.0 计算结果表明, 孔压在地裂缝处最低, 随着距地裂缝距离增加,逐渐增大, 约在水平坐标60 m 位置, 孔压达到天然状态, 超过60 m 范围受边界影响较大, 因此在理论计算中取了影响半径R为60 m。

从计算结果的数值方面看, FLAC3D6.0 流固耦合方法与理论公式的计算结果见表2。 在60 m 范围内误差均在2%以内。

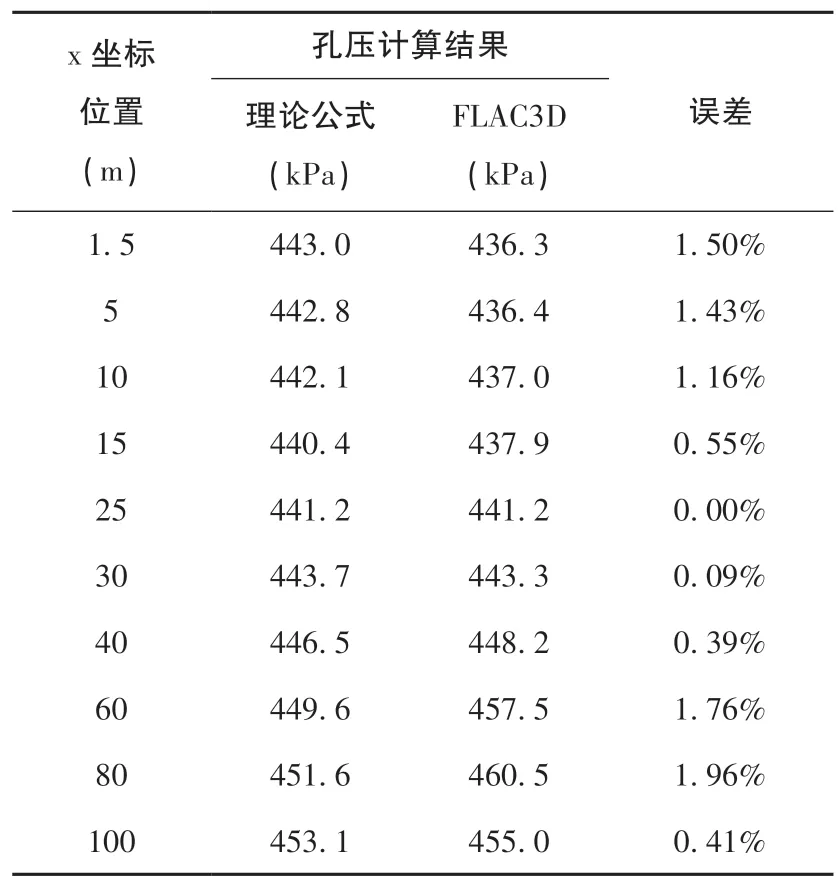
表2 理论公式与FLAC3D6.0 计算结果对比Table 2 Comparison between theoretical formula and FLAC3D6.0

4.2 地裂缝活动量分析

图5 中显示, 在水平方向上地表变形表现出受压区和受拉区相间分布的特征。 地裂缝出露地表处, 下盘相对不动, 上盘土体背离地裂缝运动, 地裂缝处土体在水平方向上处于拉张状态, 加剧了地裂缝的地表宽度。

在距地裂缝约25 m 范围内, 大致与地裂缝到抽水井之间的范围相符, 土体距地裂缝越远的点, 位移量越小, 可以推断在土体背离地裂缝方向上处于压缩状态, 距离地裂缝25 m～70 m 范围内的点, 距离地裂缝越近的点, 向着地裂缝方向水平位移越小, 距离地裂缝越远的点, 向着地裂缝方向水平位移越大, 可以推断在这个范围内, 地表土体向着地裂缝方向处于压缩状态, 曲线的斜率随着距离地裂缝距离的增加由陡逐渐变缓, 表明压缩的程度逐渐减弱。

距离地裂缝70 m 以外, 随着距离的增加土体向着地裂缝方向位移量不断减小, 曲线的斜率随着距离地裂缝距离的增加逐渐变陡, 表明土体处于拉张状态, 且拉张的程度逐渐增强, 在拉张较强的边缘区域, 易产生拉裂破坏。

图6 中, 土层在竖直方向的变形也显示出拉压相间分布。 在第一个隔水层, 即承压含水层上部的隔水层内, 从地表向下, 位移逐渐增加, 在底部稍减小,表明在该层总体处于拉伸状态, 在底部附近处于压缩状态。 在承压含水层内, 位移量随着深度增加而减小, 该层土体处于压缩状态。 在承压含水层下部的隔水层内土体也处于压缩状态, 但其变形量较上部土层相比小很多。

抽水引起的上盘土体沉降是地裂缝活动的直接原因, 地裂缝的活动量主要由开采承压含水层以及其上部地层提供, 如图6 和图7。 粉质粘土隔水层变形量大, 提供的地裂缝活动量大, 砂土含水层相对变形量小, 也能贡献地裂缝的活动量, 含水层的厚度增加,隔水层的厚度相对减小, 上下盘差异沉降量减小, 地裂缝的活动量减小。

土体的压缩过程也是排水过程, 第一个隔水层下部压缩导致孔隙水向上渗流, 减缓了上部土层的压缩, 形成了相对的拉伸区, 这也减缓了地裂缝的活动。

地裂缝的产状也影响着其活动量, 地裂缝倾向上盘, 在竖直方向上对土的沉降提供了一个阻力, 水平方向上使得距地裂缝较近的土体发生的压缩, 增大了上盘土体沉降的阻力, 一定程度上阻碍了地裂缝活动量的增加。

5 结论

本文基于抽水引起地裂缝活动的机制, 选取了地裂缝活动的理想地层结构, 建立了地裂缝活动量计算模型, 借助FLAC3D6.0 软件采用完全流固耦合方法进行求解, 结论如下:

(1) 抽水作用引起了地裂缝上下两盘差异沉降,导致了地裂缝的活动。 地裂缝错断了含水层, 影响了抽水过程中孔隙水压力的分布和地裂缝的发展过程,同时地裂缝产状也影响着地裂缝的发展。

(2) 在承压含水层中开采地下水, 抽水井的位置距离地裂缝相对较近, 地裂缝作为隔水边界, 影响了孔压的分布, 基于完全流固耦合方法计算的含水层孔压分布, 从地裂缝向上盘逐渐增大, 对比隔水边界的稳定井流公式, 分布形式稍有差异, 数值上在2%的误差以内。

(3) 流固耦合方法计算地面沉降考虑了孔隙水压力与变形相互影响, 在竖直方向上土层的压缩和拉伸变化影响孔压的变化, 影响着地裂缝活动量。

(4) 地裂缝产状倾向上盘, 在竖直方向上阻碍了沉降, 在水平方向上土体发生压缩, 增加了上盘土体向下运动的阻力, 在一定程度上减弱了地裂缝的活动。

(5) 地裂缝活动量主要由开采层及其以上地层提供, 粉质粘土隔水层贡献量大, 砂土含水层贡献量相对小, 含水层厚度增加, 相对隔水层厚度减小, 地裂缝活动量减小。

(6) 在地表地裂缝出露处土体处于拉张状态, 加宽了裂缝宽度, 距离地裂缝较近的土体由于地裂缝产状的影响处于压缩状态, 随着距地裂缝距离增加, 土体由压缩状态变为了拉伸状态, 主要受到抽水井沉降漏斗的影响, 在抽水影响的边缘处易产生拉张破坏。