基于Workbench的齿轮齿廓修形研究

刘菡华

（闽北职业技术学院，南平 353100）

0 引言

变速器总成中最主要的噪声源来自齿轮噪声，如何提高齿轮的制造质量和啮合特性，是直接影响变速器噪声的关键所在。因为不同的使用前提、承受载重的变更以及速度的频繁切换，每一齿轮的运转条件均是变速、变载的。在这样多变的情况下，受传递负载的影响，变速器工作时，轮齿、轴承、轴和箱体等各个零部件都会产生不同程度的弹性变形。而与齿轮相关的弹性变形会引起齿轮齿廓和齿向方向上的畸变[1]。

考虑齿轮的制造成本，一味地提高齿轮制造和安装精度来改善齿轮的运转效果是不可取的。因此近年来，各种“轮齿修形”方法被运用到高参数的轮齿加工中。它能使啮合齿面的载荷分布较为均匀，降低因轮齿受载变形和安装制造误差导致的啮合冲击，因此“轮齿修形”技术在齿轮加工中受到了重视。

根据产品特点以及自身的制造加工能力确定生产齿轮的修形方法，已经成为众多齿轮制造企业的核心技术。本文选取某企业量产的一对齿轮作为研究对象，采用workbench 软件对修形前后齿面接触应力的变化状况作为分析依据，寻求一种适合该对齿轮的修形工艺，达到改善齿轮承载能力的目的，为齿轮降噪提供一定的参考。

1 齿轮副仿真模型建立

齿轮参数如表1所示，用solidworks 软件建模后，导入Workbench。添加材料设置为20CrMnTi，定义接触对（在接触状态下，将小齿轮的4 个齿面设置为接触面，大齿轮的4 个齿面设置为目标面），然后进行网格划分、设置边界条件，在小齿轮内孔施加大小为175 N•m 的扭矩，得到图1所示齿轮副模型[2]。

表1 齿轮参数

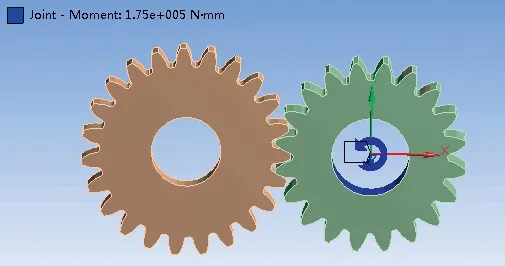
图1 齿轮副仿真模型

2 齿廓修形有关参数计算

齿轮的啮合传动伴随着单双齿不断地交替啮合变换，在这样的过程中，传递的载荷产生了骤变，轮齿的弹性变形也相应发生了改变。由于制造安装误差和弹性变形的存在，齿轮在啮入或啮出时发生了微小的干涉[3]。齿廓修形就是对靠近齿顶或齿根的局部进行修形，适当削去一对啮轮齿上发生干涉的齿面部分。

齿廓修形有3 个要素：修形长度Δhmax、最大修形量Δxmax 和修形曲线。修形示意图如2 所示。

2.1 最大修形量

修形量的选择是一个关键的问题，过小的修形量不利于改善啮合的冲击，过大的修形量又会造成齿轮的重合度降低，导致误差，不利于减振降噪。运用材料力学的方法、弹性力学方法、经验公式及有限元法，都可以确定轮齿的最大修形量。有限元技术建立在弹性力学理论基础上，对具体的工况进行了分析，所得的结果是轮齿接触弯曲、剪切等各种变形的组合，能够准确反映齿轮的应力和变形状态。本文对大小齿轮的齿顶分别修形，通过有限元提取啮入点和啮出点的变形量，与某一最大修形量经验公式进行对比，分析及过程如下。

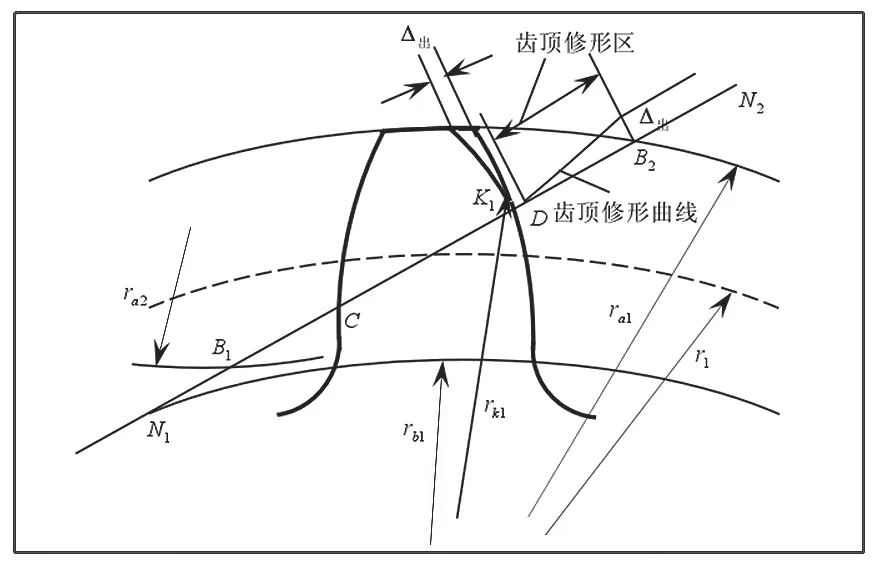
图2 齿廓修形参数示意图

图3a 是齿轮刚啮入状态，小齿轮是主动轮，带动大齿轮运转。“1”处为小齿轮某齿刚刚进入啮合时的状态，理想情况下是不存在变形的。但实际啮合中，由于“2”和“3”处齿面接触弹性变形的影响，小齿轮在啮入的瞬间，大齿轮的齿顶与小齿轮的齿根位置发生少量干涉“Δ”，形成啮入时的冲击。这个干涉量相当于大齿轮齿顶的修形量。

同理，如图3b 所示，“4”处为小齿轮某齿退出啮合的瞬间，受到“1”、“2”和“3”处齿面接触弹性变形的影响。小齿轮在啮出的瞬间，小齿轮的齿顶与大齿轮的齿根位置发生少量干涉“Δ”，造成啮出时的冲击。这个干涉量相当于小齿轮齿顶的修形量。

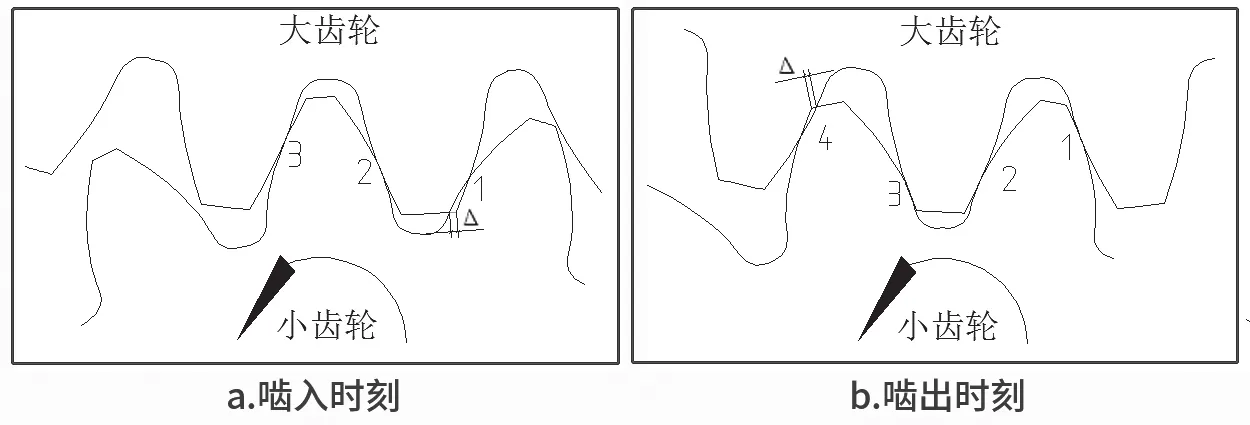
图3 齿轮啮合示意图

基于以上分析，修形量提取的有限元计算，分别建立啮入和啮出状态的2 个齿轮模型，构建子模型。采用扫掠法（swept meshing）对网格进行划分，再用Edge size 命令对接触区域进行网格的细化，其属性下的Element sizes 设置为200.0 μm。接触对的设置同粗糙的模型。在新出现的submodeling 中，单击“选中”，在右键菜单中添加位移。选择新模型的6 个面作为导入位移边界，导入粗糙模型对应处的位移。

啮入状态如图4a 所示，有限元分析后，提取“1”处大齿轮齿顶的位移值，即为大齿轮齿顶的最大修形量。同样在啮出状态，如图4b 所示，提取“4”处大齿轮齿根的变形量作为小齿轮齿顶的最大修形量。因此，确定出大齿轮的齿顶修形量是12.7 μm，小齿轮的齿顶修形量是8.8 μm。

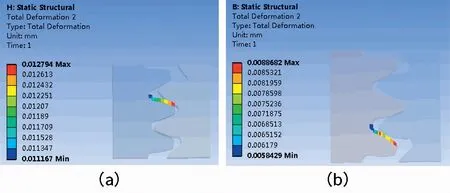
图4 变形量提取结果

2.2 齿廓修形曲线与修形长度

本文选取walker 修形曲线进行修形，修形曲线的方程如下。

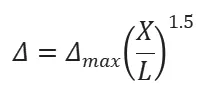
式中L——单双齿啮合区分界点到啮入点（或啮出点）的距离，即为修形的长度

X——啮合点的相对坐标，沿啮合线，原点在单双齿交替点处

Δ——距离为X 时的修形量，Δmax为最大修形量

建立修形齿轮渐开线模型（图5），用作图法求得齿轮的实际啮合线的长度B1B2=12.391，求得重合度εα=1.399，则修形长度为：

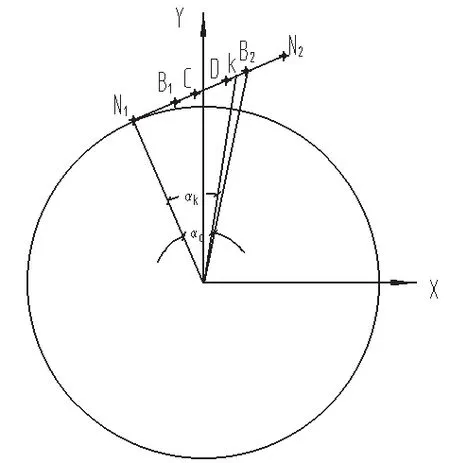
图5 啮合点相对坐标计算示意图

L=12.391×（εα-1）/εα=3.534

即B1C=DB2=3.534

本文采用主、从动齿轮齿顶都修形的方案，DB2是主动轮齿顶的修形区，B1C是被动轮齿顶的修形区。若要求得修形曲线公式中X的长度，即求DK的长度，则有：

X=L-KB2

所以

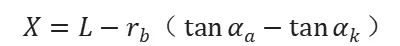
其中,αk为渐开线发生线与渐开线交点所对应的压力角。

3 齿廓修形效果验证

通过瞬态动力学检验该方案的齿廓修形效果。瞬态动力学分析是通过确定结构在瞬态载荷、静载荷及简谐载荷的随意组合下,随时间变化的应变、位移、应力及力的关系,来分析判断承受任意随时间变化载荷的结构动力学响应的一种方法。考虑到瞬态动力学的计算量大，将齿轮模型简化为5 齿后导入Workbench 中。

添加材料属性：点击“Engineering Data”，创建名称为20CrMnTi 的材料，设置密度为7 800 kg/m3，弹性模量2.07×105MPa，泊松比0.25。

定义接触对：以左侧大齿轮齿面为接触面，右侧小齿轮齿面为目标面，设置接触对的类型为“Frictional”，摩擦系数设置为0.1。使用“Augmented Lagrange”算法，设置初始接触状态为“Adjust to Touch”，FKN 取1（图6）。

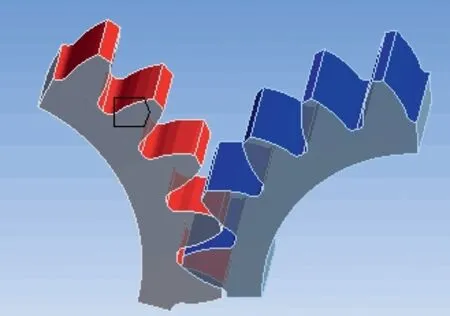
图6 定义接触对

网格的划分采用“Sweep Method”进行网格划分，“Relevance center”设置为“Mediun”，并对接触区域使用“Edge sizing”将网格尺寸设置为0.4 mm，进行网格细化处理。划分后的网格如图7所示。

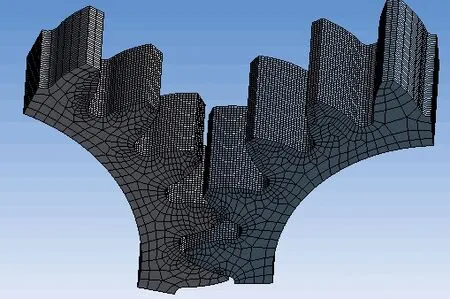
图7 网格划分

载荷和时间步的设置：在大小两个齿轮中心施加一个相对于地面的转动副，设置小齿轮为主动轮，在小齿轮上施加251.33 rad/s 的转速，大齿轮上施加201.25 N•m 的阻力矩（图8）。载荷步数设置为2，在第一个子步中，设置“Step End Time”为1×10-4s，采用“substeps”的方式，“Number Of Substeps”设置为1。在第二个子步中，第2 步“Step End Time”设置为5×10-3s。“Auto Time Stepping” 设置为On，“Define by”设置为time，“Weak springs”设置为off，“Large Deflection”设置为On。初始时间步为1×10-5s，最小时间步为1×10-8s，最大时间步为2×10-5s。

图8 载荷设置

求解：选择未修形前和修形之后齿轮的一个轮齿从啮入到啮出的等效应力求解（图9、图10）。

图9 未修形的齿轮啮入、最大应力及啮出状态

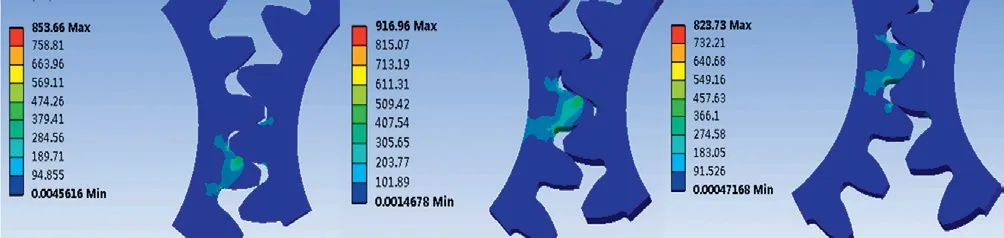
图10 修形后的齿轮啮入、最大应力及啮出状态

将采集到的接触应力数据反映到曲线图（图11、图12）中，可以清楚地看到，该对齿轮在修形前和修形后一个齿从啮入到啮出整个过程的应力变化。该过程是一个双齿到单齿再到双齿啮合的一个过程，整个齿轮副的啮合就是不断重复着这样的变换。单齿啮合区由于啮合的区域较少，接触应力会最大。

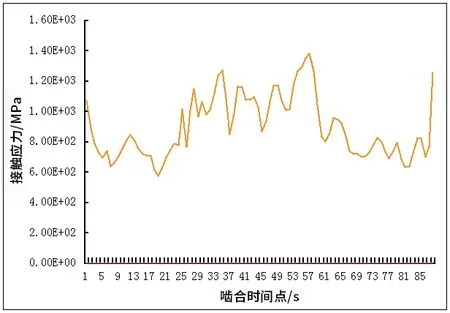
图11 修形前接触应力变化图

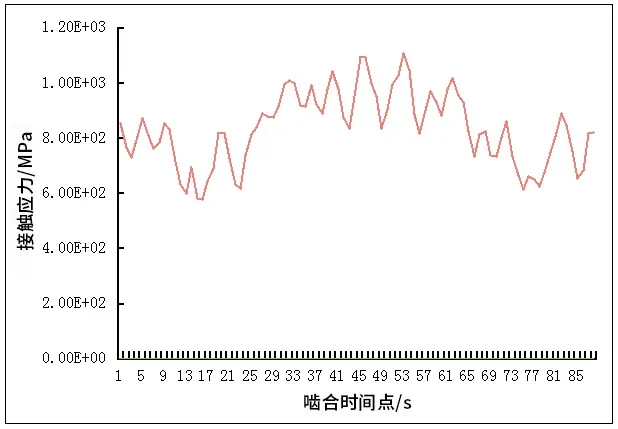
图12 修形后接触应力变化图

由修形前接触应力变化图可知，单齿啮合区的接触应力最大达1 384.00 MPa，啮入时的接触应力为1 072.10 MPa，啮出时的接触应力为1 256.80 MPa，在啮入和啮出时出现了较大的应力突变。

在修形后接触应力变化图可以看出，修形之后，单齿啮合区的接触应力最大为1 109.70 MPa，啮入时的等效接触应力为853.66 MPa，啮出时的等效应力为823.73 MPa，啮入和啮出时的应力分别降低了20.37%和34.46%。

同时，单齿最大的啮合应力也有降低，整个啮合应力曲线比未修形前过渡得更加平缓。该种齿廓修形方法使整个载荷分布较为均匀,降低因轮齿受载变形导致的啮合冲击和振动，提高承载能力，增加使用寿命，有利于降噪。

4 结束语

本文运用有限元法确定最大修形量，计算确定出修形曲线上的点的坐标，建立修形前后的齿轮模型。之后合理施加约束和载荷，进行瞬态动力学分析，模拟齿轮的啮合状态，仿真验证了通过齿廓修形可以有效改善啮合中的应力突变，取得了较好的效果。