基于ELM的齿轮钢淬透性预测模型

赵艺琪，聂小龙，赵四新，高加强，刘新宽

(1.上海理工大学 材料与化学学院，上海 200093;2.宝钢研究院，上海 201900)

齿轮钢在汽车、铁路、船舶等工程机械中广泛使用，是特殊合金钢中要求较高的关键材料，是保证安全的核心部件制造材料。近几年，齿轮钢正朝着高性能、长寿命、运行平稳、低噪音、高安全性、低成本、易加工等多品种方向发展[1]，其中20Cr钢是一种广泛使用的低碳合金齿轮钢。淬透性是评价齿轮钢质量的重要指标，钢材淬透性稳定与否对齿轮热处理后畸变影响很大。淬透性带宽主要是由不同炉次钢材化学成分控制偏差或同一炉次钢化学成分的不均匀性所致。轿车齿轮钢淬透性一般要求全带控制在6 HRC以下，并且要求同一炉钢材的淬透性带宽不大于4 HRC[2]。而钢的淬透性预测是实现窄淬透性带宽精确控制、降低热处理畸变的重要手段。

1938年Jominy用端淬试验法得出端淬曲线以来，相关研究人员循着定性、半定量和定量研究的途径，对端淬曲线做了大量研究工作，现已提出一些定量计算公式。新版《机械工程手册》采用的是由余柏海先生建立的非线性端淬曲线通用计算公式，反映了钢端淬曲线的基本形态和变化规律，堪称定量研究钢的淬火工艺与组织结构、力学性能关系的重要成果[3-4]。而美国汽车工程师学会则推荐了线性拟合公式来计算端淬曲线[5]。但是用这些方法得到的预测值与实测值之间还是存在一定的差距，这使得这些方法在实际生产中的应用存在局限性。因此，只有利用更加先进和准确的数学方法，开发一种准确度高、使用快捷方便的数学模型，用于齿轮钢淬透性的预测问题，才能解决齿轮钢淬透性预测面临的难题。

极限学习机(Extreme learning machine, ELM)是一种基于单隐层前馈神经网络(Single-hidden layer feedforward neural network, SLFN)的新算法。2003年，南洋理工大学黄广斌首次提出了该算法[6]，相对于传统的神经网络学习算法，该运算速度更快且泛化性能更优，不需要自身设置训练参数，可以随机生成隐含层神经元的阈值以及输入层与隐含层之间的连接权值，因此在不丢失精确度的同时，大大提升了运算效率。本着学习和探讨的精神，本文首次尝试运用拟合齿轮钢端淬曲线计算式，以提高端淬曲线精度，实现淬透性和化学成分之间的双重反馈，并得到较为满意的结果[6-11]。

1 ELM预测模型的构建

ELM是为改进BP(Back propagation)神经网络训练过程中泛化能力差等问题而提出的一种基于单层前馈神经网络的特殊的SLFN。ELM在训练之前可以随机地产生输入层与隐含层之间的连接权值W和隐含层神经元的阈值b，只需要确定隐含层神经元的激活函数和隐含层神经元个数，即可利用最小误差化的限制条件计算出输出权重β。本文所用的ELM预测模型结构如图1所示。

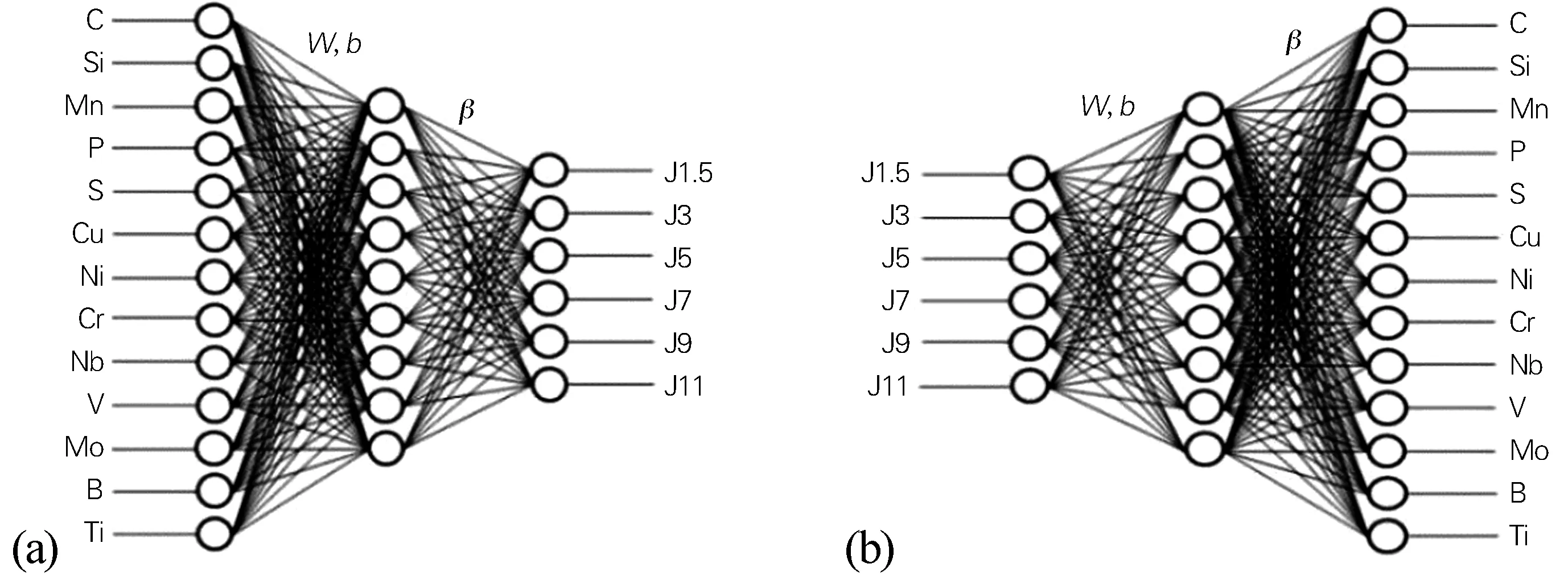
图1 ELM神经网络结构

1.1 淬透性试验

本文选择某工厂生产20Cr齿轮钢的成分和端淬曲线数据作为ELM预测模型的训练样本，试样外形如图2(a)所示，取样方法按照GB/T 225—2006《钢 淬透性的末端淬火试验方法(Jominy试验)》从φ60 mm规格的成品轧材上取得，末端淬火试样按照GB/T 5216—2014《保证淬透性结构钢》中的技术条件900 ℃×60 min正火、880 ℃×60 min端淬处理进行。选取同一炉次两个具有对比性的试样，其生产过程与所采用工艺完全相同。试样的平均成分通过直读光谱仪和化学分析法测试得到，测试结果见表1。本文按照GB/T 225—2006要求在端淬试样上与规定测试面90°及45°角的表面磨制硬度测试面，如图2(b)所示，利用数显塑料洛氏硬度计(XHRS-150)对测试面J1.5(从试样端淬末端测量为1.5 mm的截面)、J3、J5、J7、J9、J11位置处的硬度进行测试，测试结果见表2。

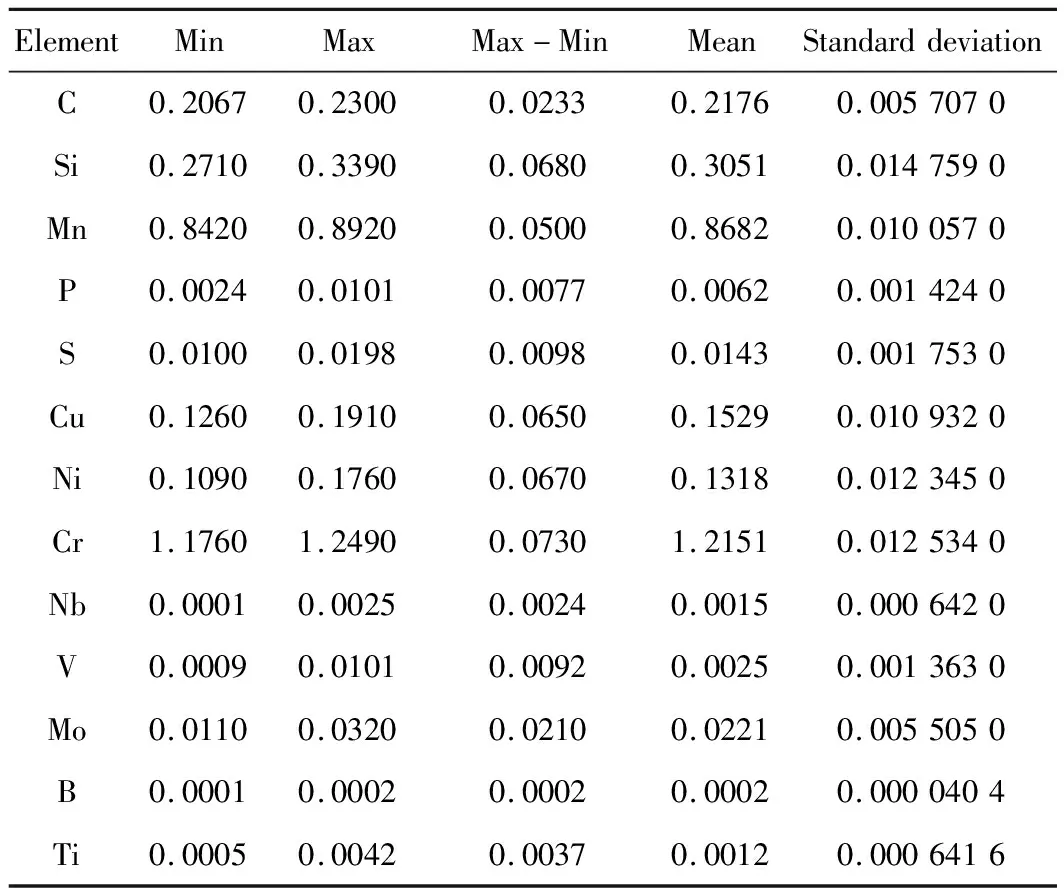
表1 20Cr齿轮钢化学成分测试结果(质量分数，%)

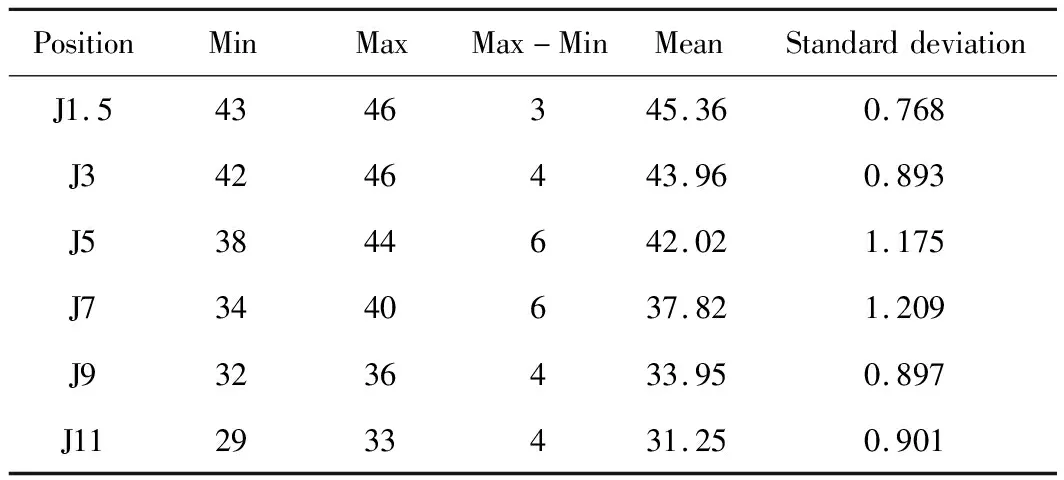
表2 20Cr齿轮钢端淬硬度值测试结果(HRC)

1.2 齿轮钢预测淬透性模型

利用Matlab R2018a软件对20Cr齿轮钢淬透性进行模型建立及预测。数据共有146组，随机选取其中100组数据用作训练，剩下的46组数据作为测试数据。

采用ELM算法模型的网络结构为n×i×M，其中，输入层个数n=13，中间层i=9，输出层M=6。网络的13个输入是钢的常用成分，分别为C、Si、Mn、P、S、Cu、Ni、Cr、Mo、Nb、V、B、Ti，输出值为齿轮钢J1.5、J3、J5、J7、J9、J11处的硬度。隐含层在神经网络中起抽象作用，它可以从输入层中提取特征。一般来说，隐含层层数越多，处理数据的能力越强，但是，增加隐含层层数势必会增加训练的复杂程度，导致样本数量的增加以及训练时间的延长。因此一般选择一个隐含层，然后按需要增加隐含层。本文所用模型为单层。隐含层节点数的选择十分复杂，一般与输入层和输出层个数相关，且节点越多，精确度越高。模型中，在比较了计算速度和预测结果后，中间层选择了9个节点。

1.3 齿轮钢化学成分预测模型

本文还尝试利用ELM模型根据端淬硬度曲线数据预测齿轮钢的化学成分。采用ELM算法模型的网络结构为n×i×M，其中，输入层个数n=6，6个输入是齿轮钢端淬曲线中J1.5、J3、J5、J7、J9、J11处的硬度；中间层i=9；输出层M=13，13个输出为齿轮钢的化学成分，主要是常见元素C、Si、Mn、P、S、Cu、Ni、Cr、Mo、Nb、V、B、Ti的含量；隐含层节点数为9。

2 试验结果分析

2.1 淬透性预测分析

图3为随机抽取进行结果验证的46个产品J1.5、J3、J5、J7、J9、J11(端淬距离分别为1.5，3，5，7，9，11 mm)的实测淬透性曲线，从图3中可以看出，实测的硬度分布波动较大，J1.5处硬度分布波动大约在3 HRC 以内，而图3(c,d)中J3、J9、J11的硬度分布波动范围达到4 HRC，个别硬度点，如图3(a,b,d)中，J5、J7处硬度分布波动范围甚至达到6 HRC，这说明实际测量的硬度波动较大，产品硬度曲线上下限宽带过大，影响了齿轮钢产品的质量稳定性。

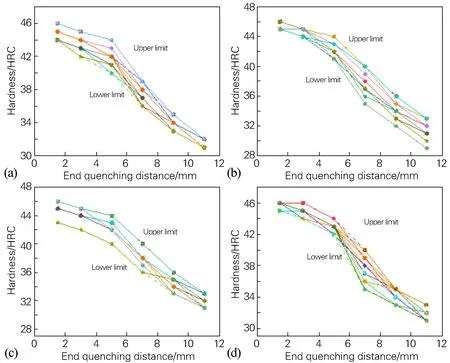
图3 齿轮钢产品淬透性曲线

图4比较了ELM根据46组化学成分数据预测的硬度值和实测值。从图4中可以看出，预测值与实测值之间的误差很小，基本上维持在±1 HRC，而且模拟的硬度波动不大，基本保持在1～2 HRC。

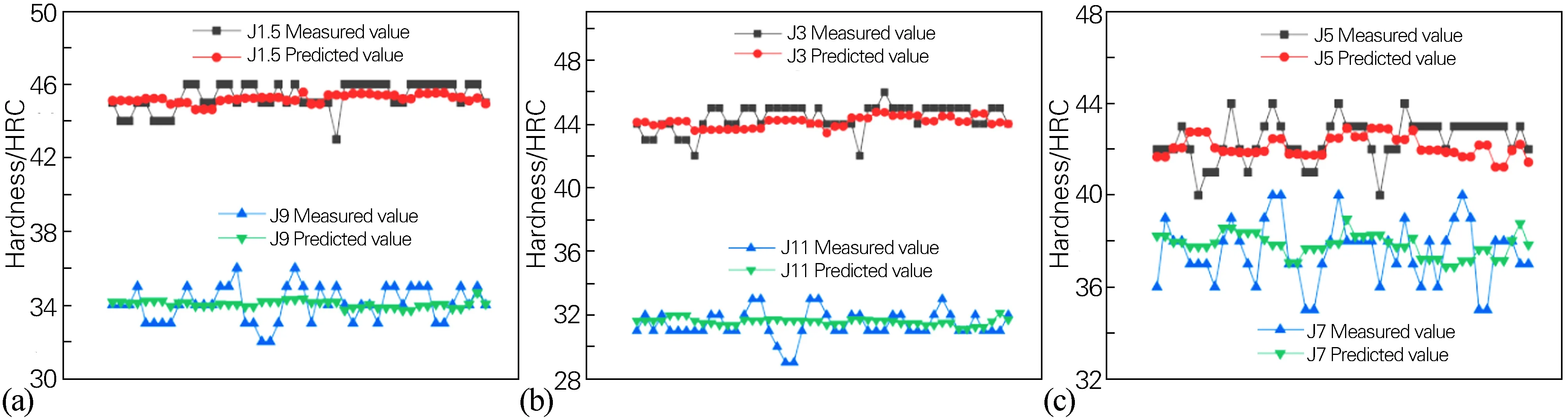
图4 不同端淬距离处试样实测硬度值与ELM预测硬度值对比

图5(a)为J1.5、J9处的预测误差分布散点图，图5中两条横线为硬度误差以1 HRC为分界以及硬度误差百分数以3%为分界的统计图。从图5(a)中可以看出，J1.5处的预测结果十分精确，误差几乎全部维持在3%以内，实测值和预测值之间的误差基本上不超过1 HRC。图5(b)为J3、J11处的预测结果，与J1.5处的预测结果相当，从误差分布图上可以看出，预测误差基本上可以维持在3%以内，不超过1 HRC。而J5、J7、J9处的预测值波动稍大，其原因在于J5、J7、J9处的实测硬度值波动非常大，从而导致预测结果与实测值之间的误差加大，即使如此，预测误差还是更多地控制在3%、1 HRC 以内。

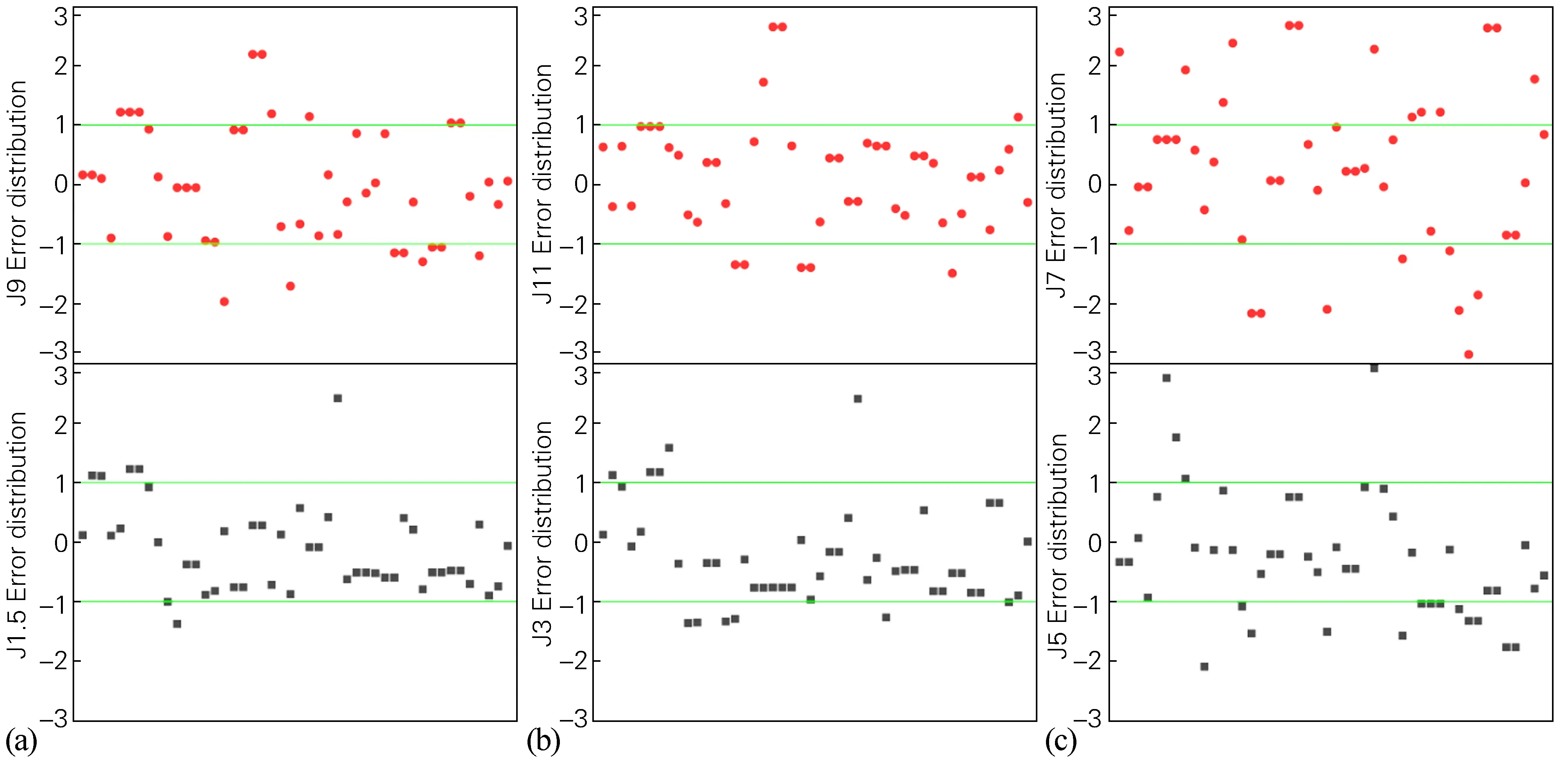
图5 端淬曲线上各硬度点的预测误差分布

图6为端淬曲线上各硬度点预测误差分布统计图，可更直观地体现图5的结论。

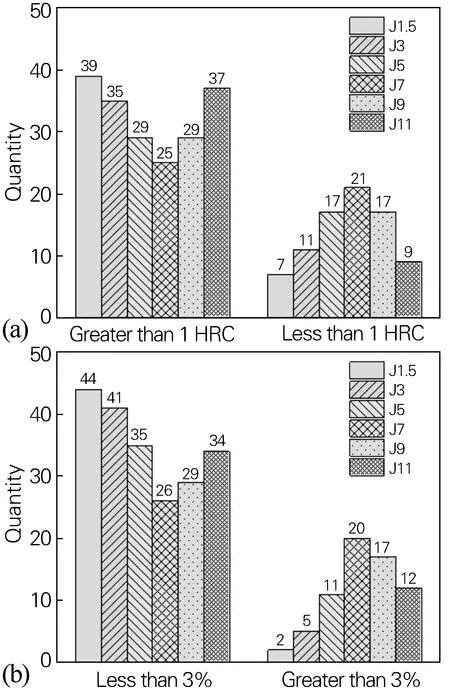
图6 端淬曲线上各硬度点预测误差分布统计图

2.2 ELM预测模型与传统预测方法的比较

图7为ELM与非线性方程法[12]、BP神经网络建立的预测模型计算结果之间的对比。由图7可知，ELM的预测精度最高，其次为BP神经网络，非线性方程法预测效果最不理想。表3可以更加直观地反应3种方法的预测精度，在6个硬度点上，ELM的硬度均方根误差均较小，且相对非线性方程法，往往相差2～3倍，整体均方根误差缩小20%左右。非线性方程法预测值往往比实测值高2～3 HRC，预测精度不高，与实际值相差较大。BP神经网络方法因为追求与每个实测值之间的逼近程度，造成预测值存在上下波动，局部某些值存在与实际值相差很大的情况。而ELM预测值基本稳定在一个中间值，上下波动很小。

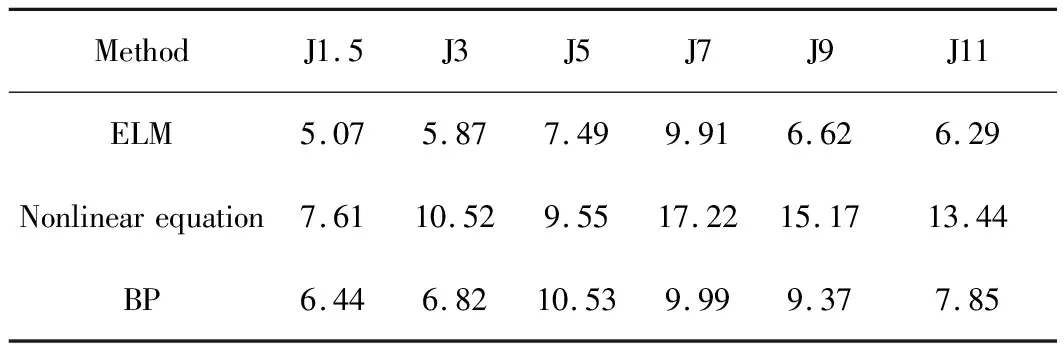
表3 ELM与传统方法预测各点硬度均方根误差(HRC)

由图7可知，BP神经网络的预测结果整体精度不高，这跟BP神经网络本身存在的弊端有关。而相比BP神经网络方法，ELM输入层和隐含层之间的连接权值和隐含层的阈值随机确定，确定后不需要调整，也就是说，与传统的神经网络相比，减少了前端的运算量，速算速度加快。同时，隐含层和输出值之间的连接权值也不需要调整，而是通过多元回归的方式确定，与回归分析中拟合系数的方法大致相同，算法的基本思想发生改变；另外，由于ELM仅需求解输出权重，用到的方法是回归分析法，所以它的学习过程更容易在所有单元都是极小值的情况下收敛，即不存在局部最优解的问题。因为ELM用到了回归分析的基本原理，数据处理时经过了不断的学习和训练，所以预测精度更高更精确。

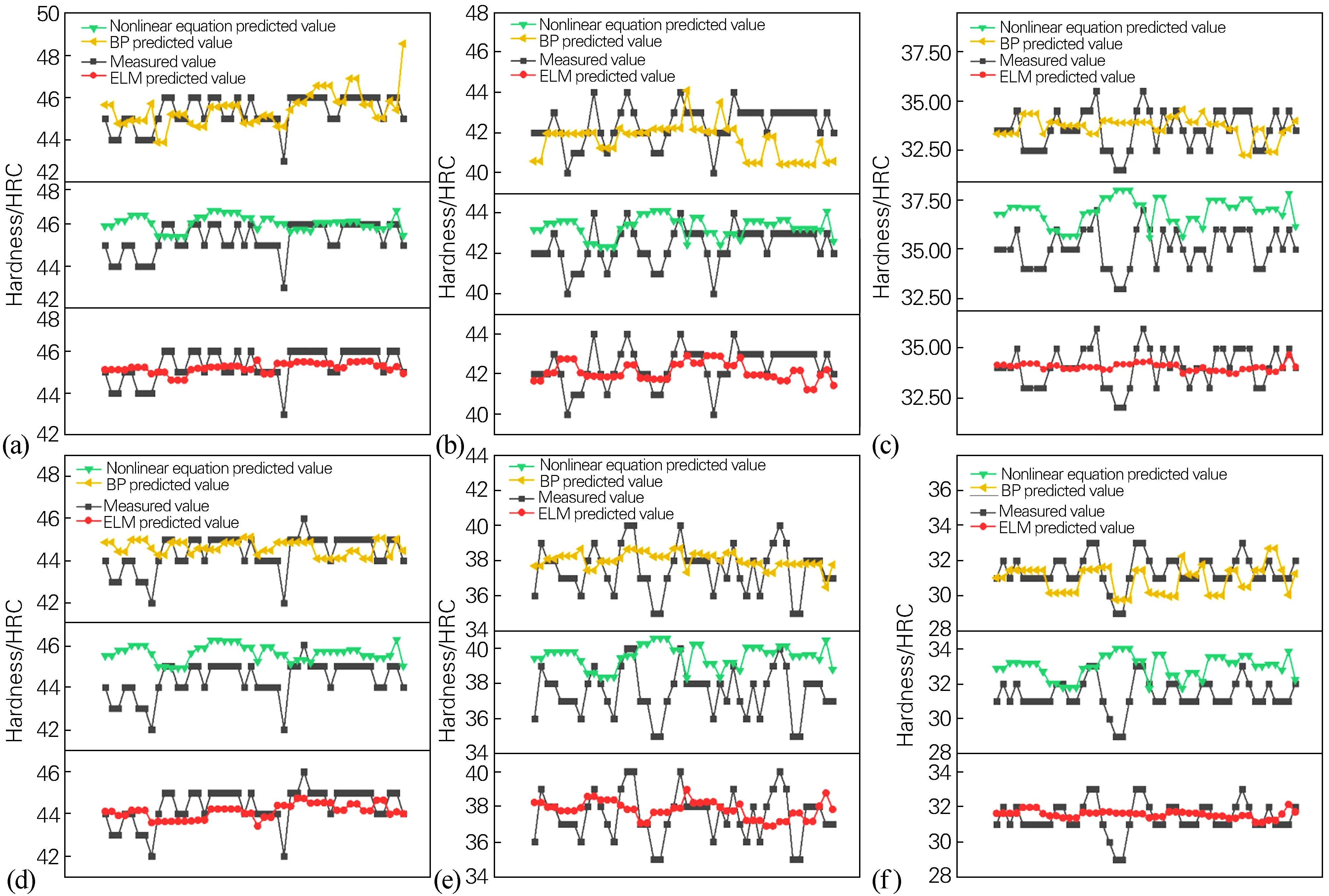
图7 ELM与传统方法硬度值对比

2.3 成分预测分析

本文还用ELM模型从端淬硬度曲线反推齿轮钢的化学成分，计算结果如图8所示。图8(a)为C、Mn、Cr 3个合金元素预测值与模拟值的散点图，图8(b～d)为C、Mn、Cr 3个合金元素误差百分数的散点图。C元素预测值和实测值之间的误差几乎小于5%，Mn、Cr元素的误差分数分别小于3%和2%，也就是说用ELM可精确预测齿轮钢的化学成分。

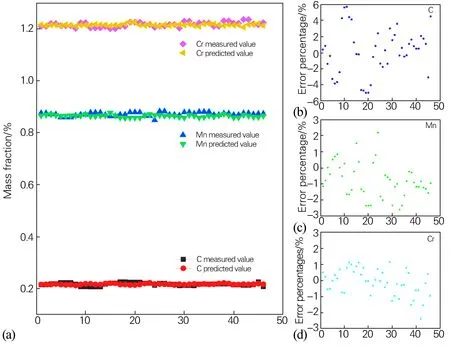
图8 C、Mn、Cr组分实测值与ELM模拟值对比(a)及误差分布(b～d)

2.4 ELM模型在齿轮钢淬透性硬度带宽原因分析上的应用

齿轮钢材料不可避免存在不同程度的成分偏析，甚至端淬试样的不同部位成分也不相同，从而造成较大的硬度波动。而ELM模型根据测量的淬透性硬度值计算齿轮钢测试部位的成分，可以很方便地对成分偏析造成的硬度带宽进行评估。如表4所示，同时测量某个试样J5位置的部位1和部位2的硬度值(见表5)，再根据测量成分预测其硬度值，发现部位1根据成分预测的硬度值(46.35 HRC)和实际测量值(45.14 HRC)吻合很好，误差只有0.4%。而部位1根据熔炼时给出的成分预测的硬度(42.76 HRC)和实际测量值(45.14 HRC)相差2.38 HRC，存在5.2%的误差。部位2也符合上述规律。这说明，两个部位的硬度偏差主要是由成分偏差引起。

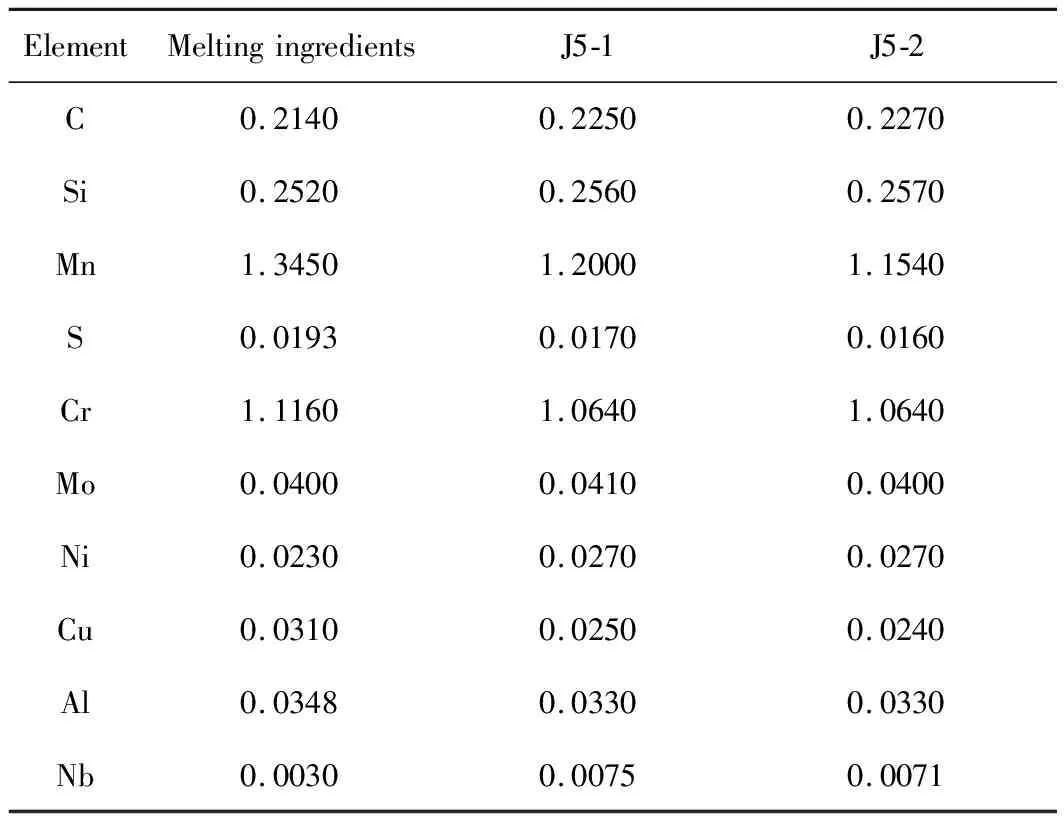
表4 某试样J5截面两个不同部位测量的成分(质量分数，%)

表5 实测及根据成分预测试样J5截面不同位置处的硬度值对比(HRC)

3 结论

1)本文首次尝试运用ELM模型拟合20Cr齿轮钢端淬曲线，实现了淬透性曲线和化学成分之间的双重反馈，并得到较为满意的结果。

2)ELM可以根据齿轮钢的化学成分预测其淬透性，计算精度明显好于传统计算方法,均方根误差缩小20%左右。

3)ELM也能通过齿轮钢淬透性硬度曲线反测化学成分，元素含量误差在5%以内。