基于电化学的改进等效电路模型的SOC估算


摘 要:提出了一种基于电化学的拓展等效电路模型(Extend Equivalent Circuit Model,EECM),并用该模型进行电池荷电状态(State of Charge,SOC)估算。根据电化学机理和等效电路模型(Equivalent Circuit Model,ECM)对比得到ECM物理过程缺失的部分,考虑在ECM中加入固相扩散、反应极化和液相极化对电池端电压的影响。使用遗传算法在混合功率脉冲特性(Hybrid Pulse Power Characteristic,HPPC)工况下进行参数辨识,来获得全局最优模型参数;使用拓展卡尔曼滤波(Extended Kalman Filter,EKF)进行SOC的估算。实验结果显示,在城市道路循环(Urban Dynamometer Driving Schedule,UDDS)下,模型的估计误差小于0.5%。所建立的模型和SOC估计器动态性能良好,计算量较小,有望在电池管理系统(Battery Management System,BMS)中使用。
关键词:电化学;等效电路模型;荷电状态;拓展卡尔曼滤波
中图分类号:TM911.3 文献标志码:A 文章编号:1671-0797(2022)07-0028-05
DOI:10.19514/j.cnki.cn32-1628/tm.2022.07.008
0 引言
SOC是BMS所有算法的基础,良好的SOC估算能使BMS更好地进行能量管理,提高锂电池的能量使用效率,延长电池的使用寿命。此外,准确的SOC估算对电动汽车的运行性能有重要影响。SOC不能直接或通过传感器测量,因为锂离子电池本身是一个封闭的系统,且SOC有赖于各种因素,如电池寿命、环境温度和电池复杂的化学反应[1]。因此,研究对SOC进行实时估算的高精度方法至关重要。
1 基于電化学的EECM
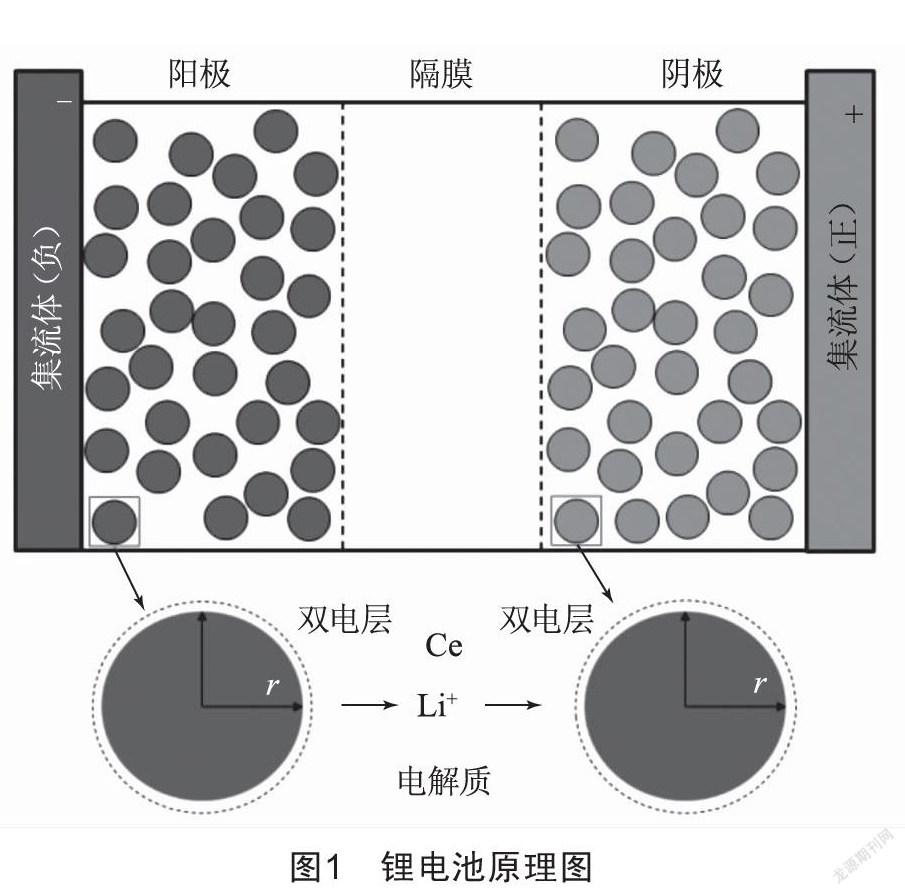
锂电池从负极集流体(x=0)到正极集流体(x=L)由以下三部分组成:电极负极、隔膜、电极正极,每一个电极连接到一个金属集电器上。锂电池的主要工作原理如图1所示。
以放电的电池阳极为例,电池内部主要包含以下几个过程:(1)固相扩散,锂离子从活性粒子内部扩散到粒子表面;(2)在活性粒子和电解质溶液表面发生化学反应,锂离子脱嵌;(3)锂离子在电解液中从阳极经过隔膜扩散到阴极表面;(4)在阴极发生化学反应扩散到粒子内部[2]。
传统的ECM通常采用电阻和电容组成的RC网络来反映电池的动态特性[3]。常用的等效电路模型为二阶RC等效电路模型,如图2所示。OCV(SOC)为电池的开路电压,通过HPPC实验测得,Rohm为电池内部电解液电阻和接触电阻,Udl为双电层效应造成的电压损失[4]。
在本文中欧姆内阻Rohm通过HPPC实验计算得到,为了适应不同倍率,为欧姆内阻增加一个修正系数Kr,Kr在后文通过遗传算法在全局精度的辨识得到。由欧姆内阻引起的压降为:
Uohm=IRohmKr(1)
式中:I为电池充放电电流。
双层的电压降UDL j用两个一阶过程代表,双电层的压降为:
DL j=-+,j=1,2(2)
传统的ECM和电池电化学过程相比,ECM缺失了固相扩散损失电压、锂离子在粒子表面发生化学反应造成的电势差以及液相扩散造成的电解液电势差。
针对模型物理过程的缺失,将ECM进行拓展。锂电池的端电压性质更多由固相表面锂离子浓度反映[5]。宏观的SOC不能很好地反映电极动力学。SOC在P2D模型中定义如公式(3)所示,欧阳明高对电极表面SOC提出定义如公式(4)所示:
SOC=(3)
SOCsurf,i=SOC(4)
式中:Cs,i为电极平均锂离子浓度;Cs,i,0为SOC为0时的电极锂离子浓度;Cs,i,100为SOC为100时的锂离子浓度;Cs,i,surf为电极表面锂离子浓度;SOCsurf,i为表面SOC;下标i=n、i=p分别代表电池负极和正极。
在宏观运算中,SOC通常采用安时积分法进行计算:
SOC=SOC0+dt(5)
式中:SOC0为初始荷电状态;η为电流效率(本文取1);C为电池容量。
定义表面锂离子浓度和平均锂离子浓度的差为ΔCs,i:
ΔCs,i=Cs,i-Cs,i,surf(6)
考虑电化学中固相扩散方程为时间和位置的偏微分方程[6-7]:
-r2
=0(7)
边界和初始条件为:
Cs(x,t,r)|t=0=Cs,0(8)
Ds
=0(9)
Ds
=-(10)
为了满足控制需求,需要对式(7)进行化简,本文采用三参数近似的方法对偏微分方程进行化简:
(t)+3=0(11)
(t)+30(t)+=0(12)
35[Cs,i,surf(t)-(t)]+8Ds,i(t)=0(13)
式中:ji为局部电流密度;Ri为粒子半径;为平均浓度流量;Ds,i为固相扩散系数。
将式(11)~式(13)的结果代入式(6)得到修正后的SOCsurf,i:
SOCsurf,i=
+
(t)-Cs,i,0/(Cs,i,100-Cs,i,0)(14)
除了固相扩散过程,对模型反应极化进行讨论,由BV方程可得:
ηact,i=arsinh
(15)
式中:ηact,i为反应极化过电势;R为气体常数;T为温度;F为法拉第常数;αi为电极交换系数;as,i为颗粒比表面积;i0,i为交换电流密度。
进一步得到反应极化的等效电阻:
Rηact,i=(16)
针对液相扩散过程,为考虑模型复杂度,将液相扩散电势的电阻设为:
Re=(A1×I+A2×I2)×t(17)
式中:A1和A2为液相扩散电阻系数;t为充电或放电时长。
综上,电池的端电压写为:
Ut=UOCV-I(KrRohm+Rηact+Re)-Udl1-Udl2(18)
式中:UOCV为电池开路电压。
根据电化学原理完成对ECM的修正,EECM如图3所示。
2 实验和参数辨识
2.1 实验装置
本文使用松下NCR18650PF电池进行实验。NCR18650系列电池属于三元锂电池,三元锂电池相能量密度较高且循环性能好,具有优异的安全性与温度性。实验台架由Arbin BT-5HC-5V/100A电池测试仪、Hongyu HY-TH-150DH恒温恒湿试验箱、测试工作站和松下NCR18650PF电池组成。本次实验在室温(25 ℃)下进行,未来将进一步考虑温度的影响。
通过HPPC实验获得UOCV和Rohm,并使用HPPC实验数据进行全局参数辨识(下一小节进行介绍)。除了HPPC实验,还进行了UDDS放电实验,用于第3节模型验证。
2.2 参数辨识
对EECM进行参数辨识,EECM需要辨识的参数有Kr、R1、R2、C1、C2、A1、A2。除了需要辨识的参数,其余电化学参数通过同类型电池的文章得到[8-9]。
由于实验采集的数据为离散的点,为了方便辨识,对EECM方程(2)(18)进行离散化:
Ut(k)=UOCV(SOCk)-U1(k)-U2(k)-(KrRohm+Rηact+Re)I(k)(19)
U1(k)=eU1(k-1)-(1-e)R1I(k-1)(20)
U2(k)=eU2(k-1)-(1-e)R2I(k-1)(21)
本文采用由荷兰J. H. Holland开发的遗传算法进行参数辨识[10]。遗传算法本质是一种高效的全局搜索方法,与其他参数辨识方法相比,它能自适应地控制搜索过程以求得最优解。遗传算法流程图如图4所示。
为了获得全局的最优解,将HPPC实验数据和模型端电压之间的均方根误差作为适应度值来评估参数,如式(22)所示,以获得最优参数。待辨识参数的上下界根据经验进行设置。
g(V)=(22)
式中:ui,k(v)为实测数据;i,k为模型输出数据。
2.3 参数辨识结果对比
辨识结果如图5所示。在HPPC工况下,在SOC中高区域,ECM和EECM都能较好地跟踪实际电压,EECM精度略高于ECM;在SOC较低区域,由于电池极化反应加剧,传统ECM误差增大,EECM精度略有下降,不过也能很好地跟踪。在全SOC范围EECM电压的均方根误差(Root Mean Square Errors,RMSE)约为5.4 mV,ECM的电压RMSE约为7.6 mV,EECM模型输出电压在全SOC范围下精度有所提高。
3 模型验证
3.1 基于EKF的SOC估算
由式(5)(20)(21),EECM的状态空间方程写为:
SOCk
U1,k
U2,k=1 0 0
0 e
0
0 0 e
SOCk-1
U1,k-1
U2,k-1+
×3 600
R11-e
R21-e
Ik-1(23)
由狀态方程(23)和输出方程(19),得到系统矩阵:xk=[SOCk U1,k U2,k]T,u=i,y=Ut,A?1 0 0
0 e
0
0 0 e
,B?
×3 600
R11-e
R21-e
,H=
SOCsurf(k-1)+
SOC(k-1)uk 1 1。
EKF算法流程如图6所示。
3.2 结果和讨论
本文在UDDS工况下进行了验证,结果如图7所示。EECM模型在全局保持较高的精度,有较好的估算效果。ECM在中高SOC下,如图7(b)所示,和EECM相比,精度略低,但也能较好地估算SOC;在放电末端,如图7(c)所示,ECM估算的误差升高。
分段计算了模型的RMSE,从图8可以看出,在全SOC范围下EECM的RMSE呈上升趋势,但基本变化不大,基于ECM的估算,在全范围也呈上升趋势,但变化范围较大,在放电末端接近1.3%。该结果说明了反应极化、液相扩散和固相扩散修正的重要性,也反映了提出的新模型的优越性,模型较小的计算量也为车载BMS系统提供了条件。
4 结语
本文提出了一种基于电化学的EECM,通过ECM和电化学过程对比,在二阶RC模型中增加代表液相扩散、固相扩散和反应极化的环节。用遗传算法进行了全局参数辨识,并将EECM结合EKF进行SOC估算,在UDDS工况下进行了验证。结果表明,EECM有效地提升了模型的全局精度,在放电末端SOC估计精度提升50%以上,模型的动态性能良好,计算量较小,适用于车载BMS。未来将进一步考虑老化和温度等影响因素,使模型适应不同的环境工况。
[参考文献]
[1] 张树鹏,李彦明,李杰,等.基于Householder变换的改进最小二乘法估算电池SOC[J].电源技术,2016,40(2):335-338.
[2] BARSOUKOV E,KIM D H,LEE H S,et al.Comparison of kinetic properties of LiCoO2 and LiTi0.05Mg0.05
Ni0.7Co0.2O2 by impedance spectroscopy[J].Solid State Ionics,2003,161(1/2):19-29.
[3] ATTANAYAKA S,KARUNADASA J P,HEMAPALA K T M U.Estimation of state of charge for lithium-ion batteries - A Review[J].AIMS Energy,2019,7(2):186-210.
[4] 张连德.基于电化学阻抗谱的三元锂离子电池状态估计研究[D].长春:吉林大学,2018.
[5] OUYANG M G,LIU G M,LU L G,et al.Enhancing the estimation accuracy in low state-of-charge area:A novel onboard battery model through surface state of charge determination[J].Journal of Power Sources,2014,270:221-237.
[6] DOYLE M,NEWMAN J,GOZDZ A S,et al.Comparison of modeling predictions with experimental data from plastic lithium ion cells[J].Journal of the Electrochemical Society,1996,143(6):1890-1903.
[7] DOYLE M,FULLER T F,NEWMAN J S.Modeling of galvanostatic charge and discharge of the lithium/polymer/insertion cell[J].Journal of The Electrochemical Society,1993,140(6):1526-1533.
[8] LI J F,WANG L X,LYU C,et al.New method for parameter estimation of an electrochemical-
thermal coupling model for LiCoO2 battery[J].Journal of Power Sources,2016,307(1):220-230.
[9] HEENAN T M M,JNAWALI A,KOK M,et al.An advanced microstructural and electrochemical datasheet on 18650 li-ion batteries with nickel-rich nmc811 cathodes and graphite-silicon anodes[J].Journal of The Electrochemical Society,2020,167(14):140530.
[10] HOLLAND J H.Adaptation in Natural and Artificial Systems:An Introductory Analysis with Applicat-
ions to Biology,Control,and Artificial Intell-
igence[M].Massachusetts:The MIT Press,1992.
收稿日期:2022-01-06
作者簡介:王乾松(1996—),男,四川绵阳人,硕士研究生,研究方向:新能源汽车电池管理系统。

