不同渗透率下多种新能源电力系统动态安全域分析
杨金海,武家辉,王海云,姚磊
(1.新疆大学教育部可再生能源发电与并网控制工程技术研究中心,乌鲁木齐市 830047;2.国网新疆综合能源服务有限公司,乌鲁木齐市 830011)
0 引言
由于一次能源日益枯竭,新能源并网成为各个国家研究的热点。我国的西北、西南等地区风力、光伏等资源丰富,且近年来随着我国对新能源的扶持力度不断加大,风力发电和光伏发电发展迅速[1-4]。我国的新能源资源虽然储量丰富,但分布不均衡,必须依靠网架进行大容量、长距离的输送,同时也带来一系列稳定安全性问题[5]。
随着新能源接入电网的容量升高,高渗透率新能源对电力系统的影响受到越来越多学者的关注。风电机组、光伏电站较于传统同步发电机而言是2 种特性完全不同的电源,三者之间的动态特性差异较大,当一个系统内既包含同步机组又包含风电机组和光伏电站时,无法等值为一个电源,因此需要将风电机组、光伏电站、传统同步机组作为3 个独立的变量,研究不同能源种类下电力系统的安全稳定性。在已有的研究中,部分学者对单一能源形式或2 种能源形式相结合(风火打捆、光伏电站与同步机组)的安全稳定性问题进行了分析。文献[6]提出了一种传统电力系统安全域边界的构建方法;文献[7]对含直驱型风力机组的电力系统动态安全域进行构建;文献[8]提出了用于风火打捆系统中的动态安全域拟合边界方法;文献[9]利用安全域方法分析了风电并网的影响;文献[10]研究了光伏并网对电网功角稳定的影响,研究结果表明光伏并网可以改善电网功角稳定性;文献[11]对比了在预想的三相短路故障与不发生故障这2 种系统分析下,光伏并网对系统暂态稳定性的影响;文献[12]研究了不同光伏容量的并网对系统功角稳定的影响,得出光伏并网容量越大对系统功角稳定的影响越大。以上研究着重分析了单一新能源并网的稳定性影响,而并未考虑多种新能源并网参与下的系统安全稳定性,无法较好地表征系统的安全状况。
电力系统是特高维、强非线性系统,复杂电力系统更须进行降维处理后再展开研究,在多种能源形式相互耦合的电力系统中,风电、同步机组、光伏3 种能源形式对复杂电力系统的动态安全域边界影响不同,若将高维电力系统降到一维会丢失大量信息,为了得到更加准确的信息,将风电出力、同步机出力、光伏出力3 种不同的能源形式结合构造三维空间的动态安全域(dynamic security region,DSR)[13-16],该表现形式能够较好地反映系统运行的安全状态。
电力系统主电网的拓扑结构基本不会改变,常改变的是注入复杂电网系统的功率空间。随着新能源接入比例的增长,在不同新能源渗透率下电力系统的稳定特性也随之改变,考虑到新能源出力的波动性和随机性,判断系统是否处于安全运行状态变得十分复杂。因而对不同新能源渗透率下电力系统动态安全域进行深入分析具有工程实际意义,也为研究电力系统的暂态稳定性提供了详实依据。
构建不同新能源渗透率下电力系统动态安全域(dynamic security region of power system under different new energy permeability,DNEP-DSR)边界常用的求解方法有解析法[17]和拟合法[18]。文献[19]对DSR的微分拓扑性质进行了研究;文献[20]通过求解对系统注入功率的灵敏度,来构建系统的安全域边界;文献[21]根据同一失稳模式下,不同临界注入的暂态稳定域边界溢出点处法矢量的不变性推导出了超平面形式的DSR 边界表达式(线性近似)。以上文献虽然利用不同的途径构建系统的动态安全域,提高了求解速度,但同时也降低了求解精度,本文涉及到多种能源形式参与电力系统的动态安全域边界拟合,考虑到多种未知情况,采用动态差分进化(dynamic differential evolution,DDE)与改进内点法(interior point method,IPM)相结合,可以较好地解决这一问题。首先采用动态差分进化算法分析潮流数据,选出最优方向的三维功率向量,然后由改进内点法搜索最优方向附近多个系统临界点,再进行DNEP-DSR 拟合。
综上所述,本文基于单一或者两种能源形式结合的动态安全域求解方法,提出采用改进动态差分进化-内点法(dynamic differential evolution-interior point method,DDE-IPM)计算不同新能源渗透率下的电力系统动态安全域,该方法能够快速得到复杂电力系统安全域边界(边界由3 种不同种类能源形式的独立变量组成),且能够较为准确地描述系统的动态安全状态,可以为复杂能源电力系统的优化调度及判断系统的安全状态等问题提供一定参考。
1 DNEP-DSR 有功安全域数学模型
1.1 电力系统安全约束
电力系统安全稳定运行的约束包括电压幅值约束、线路电流约束、有功发电约束、安全约束集合。假设电力系统有n+1 个节点,0 表示松弛节点,1~n0表示发电机节点,n0+1~n表示负荷节点。将系统的支路分为树支和连支,分别用TB 和LB 表示。
1)电力系统电压幅值约束。
把电力系统中的节点分为2 个类型:一是发电机节点,用G表示发电机节点的集合;二是负荷节点,用L来表示负荷节点的集合。电压约束集Y定义为:

式中:YV(L)、YV(G)分别为负荷节点和发电机节点电压约束;VL、VG分别为负荷节点电压和发电机节点电压;分别为负荷节点电压最大值和最小值;为发电机节点电压最大值和最小值。
2)电力系统线路电流约束。
设θk=αi -αj为支路k的两端节点i和j间电压相角差,电力系统的线路电流约束Z为:

式中:Zθ(TB)、Zθ(LB)分别为负荷线路和发电机线路电流约束;θTB、θLB分别为线路树支电压相角差和线路连支电压相角差;分别为线路树支电压相角差和线路连支电压相角差最大值;nb为支路总数。
3)电力系统的有功发电设备约束。
如果和表示发电机母线α上注入有功功率Pα的容许上、下限,则能够满足(V,θ)的约束集Yp为:
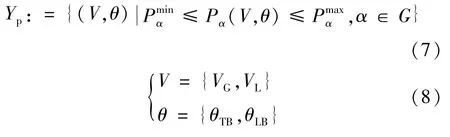
式中:V、θ为满足电压和电压相角差的集合。
4)电力系统的安全约束集合。
满足约束条件1)—3)称之为电力系统的安全约束,r表示增量形式的约束集合,并将在电压V空间中定义的集合Ψ称为安全约束集,可以表示为:

式中:ΨV(L)r、ΨV(G)r为满足负荷节点电压和发电机节点电压的电压增量集合;分别为基态发电机节点电压和负荷节点电压。
1.2 DNEP-DSR 有功动态安全域边界
新能源的高渗透率是未来电网的发展趋势,但新能源渗透率的变化会引起电网的性质改变,电网的安全稳定性也会随之改变,可以采用安全域分析不同新能源渗透率下的复杂电力系统稳定性。
图1 为电力系统动态安全域示意图,是系统全部节点的注入有功功率向量组成的节点注入功率空间,在关键设备和关键线路出口N-1 约束情况下的系统能够安全运行的所有工作点集合,由满足暂态稳定临界点超平面构成。在电力系统动态安全域中可以观察系统实时运行点与安全域边界的相对关系,可以监测系统的安全运行裕度,当系统不安全运行时,通过调整各个机组的出力,使其在最少切负荷的情况下,运行点回到安全域内部。
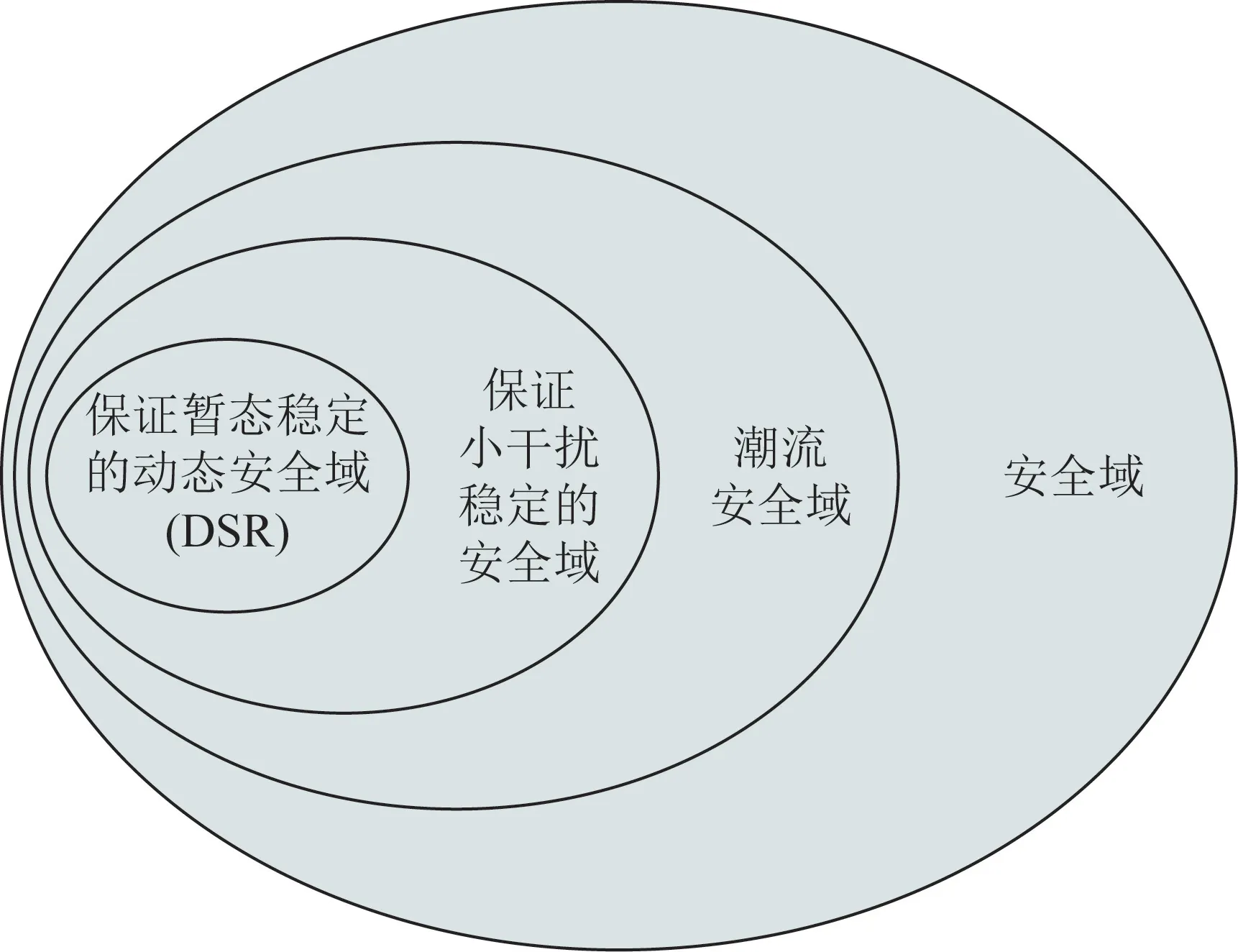
图1 动态安全域示意图Fig.1 Dynamic security region diagram
动态安全域的边界是由系统的网络拓扑结构唯一确定的,不随运行状态(如节点注入)变化而变化。对于既定的网络拓扑结构和预想事故,对于系统构建动态安全域,只需要计算一次动态安全域边界,将其动态安全域边界的超平面系数存于数据库中,需要判断和评估系统的安全运行状态时可以直接调用。
在注入的功率空间上,要满足发电机有功注入Pμ恒为正,负荷有功注入Pv恒为负,动态安全域应满足:

式中:μ为发电机节点集;v为负荷节点集。
发生短路故障事故的电力系统结构会经历事故前、事故中和事故后3 个阶段,这3 个阶段可表示为:

式中:fa[x(t)]、fb[x(t)]、fc[x(t)] 分别为故障前、故障中和故障后的系统方程;a、b、c为故障前、故障中和故障后的网络拓扑结构;τ为短路事故的持续时间。
若在某一注入功率向量y(包括3 种机组的有功注入),给定的电力系统拓扑结构经历了给定的短路事故之后是暂态稳定,这样的状态就称之为电力系统动态稳定安全,此时注入的功率y就是动态安全功率向量。注入功率空间上的动态安全域为:
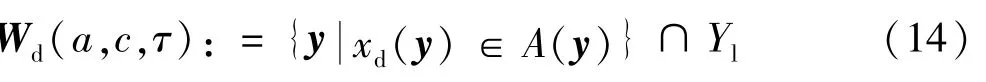
式中:Wd(a,c,τ)为对于既定的事故b和既定的事故前、后网络拓扑结构a、c唯一确定的动态安全域;xd(y)为故障清除瞬间的状态;A(y)为事故后状态空间上环绕由注入功率向量y所决定的平衡点的稳定域;Yl为各节点注入功率空间上下限的约束集合。
1.3 新能源渗透率定义
新能源渗透率fNEW为系统新能源发电功率总量PN与系统负荷电力PL总需求的比值,计算公式为:
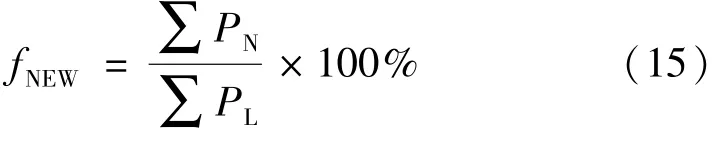
2 基于DDE-IPM 超平面拟合
2.1 超平面方程建立
求解超平面的方法有拟合法、降维法、还原法和截距法等等。本文将DDE与改进IPM 相结合,求解动态安全域的超平面系数,构建电力系统的动态安全域。实用的动态安全域是由临界超平面构成的。超平面方程可以表示为:

式中:Ps为系统的第s个有功注入功率;αs为Ps对应的超平面系数。
在采用超平面近似描述动态安全域的边界时,注入有功功率空间上的动态安全域为:
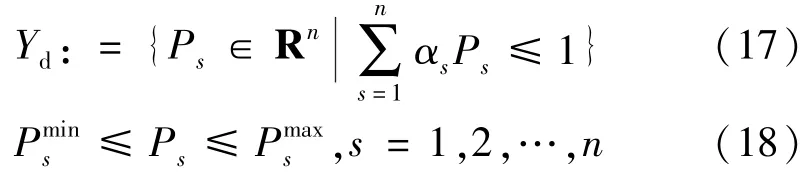
2.2 DDE-IPM 求解安全域边界
动态差分进化算法是考虑D维实数空间S⊂RD,把D维实数作为优化问题的搜索空间。DDE 是由N个D维实参数构成的一代种群在搜索空间进行并行直接搜索,得到适应度高的个体。而内点法的特点是将构造的新的无约束目标函数的惩罚函数定义在可行域内,并在可行域内求解惩罚函数的极值点,即求解无约束问题时的探索点(即初始试探点)总是在可行域内部,这样在求解内点惩罚函数的序列无约束优化问题过程中,所求得的解总是可行解,从而在可行域内部逐步逼近原约束优化问题的最优解(探索边界)。因此,本文提出结合2 种算法的优点,采用动态差分进化算法和内点法相结合来构建不同新能源渗透率下系统的动态安全域,DDE-IPM 算法的流程如图2 所示。

图2 安全域超平面系数求解流程Fig.2 Flow chart for solving hyperplane coefficients in safety region
图2 中,利用DDE-IPM 构建不同渗透率系统的动态安全域时,初始化设置种群规模为200,交叉概率为0.9,最大迭代次数为1 000,设定求解问题的维度为3 维,输出适应度大的个体,根据搜索方向和输入临界点个数,对每一次搜索到的临界运行点进行存储,得到M个临界点进行拟合。
采用图2 所示算法流程后,对于不同新能源渗透率下的电力系统动态安全域,每种情况只需要计算一次,将其参数(超平面系数、安全域图谱)存于数据库中,需要时直接调用,可以做到离线计算,在线运用,不会增加在线使用的计算负担。对于给定的新能源渗透率下的运行点,找到与之相对应的安全域图谱,即可判断该系统在某一时刻的运行点是否处于安全状态。位于安全域外是不稳定运行点,位于安全域边界上是临界稳定,而在安全域内则是稳定运行点。
3 案例分析
随着新能源渗透率不断增高,对电力系统的安全影响越来越大。风力机组、光伏电站和传统同步机组是3 种完全不同的电源形式,动态特性差异很大,研究由3 种能源形式所构成的三维空间的动态安全域,能够更加准确地反映复杂电力系统的实时运行状态。案例将风电机组、光伏电站和传统同步机组有功出力作为3 个独立的变量(G89 传统同步机组、DFIG 风电场D27、光伏电站P59),用等量的风电机组和光伏机组代替传统同步机组,研究三者共同作用对电力系统稳定性的影响。
3.1 DDE-IPM 构建DNEP-DSR
含有风电机组与光伏电站的电力系统的动态安全域边界拓扑性质是未知的,采用改进的DDE-IPM来构建DNEP-DSR的超平面边界,同时在改进IEEE 118 节点系统(见附图A1)算例中对所提方法构建的超平面边界进行时域仿真验证。
3.1.1 三种能源形式暂态有功响应
在发生预置故障后,G89 传统同步机组、DFIG 风电场(D27)、光伏电站(P59)的有功出力均骤减;故障切除后有功出力回升,但恢复速度有所差异。各个机组的有功出力如图3 所示。
从图3 中可以看到,当故障发生后,传统同步机组恢复出力的速度很慢,恢复时间为3.55 s;风力机组的恢复速度很快,恢复时间为1.46 s;光伏电站恢复速度迅速,恢复时间为0.38 s。对比3 种能源形式在故障后的出力曲线,传统同步机组恢复速度较慢,惯性较大,风电机组和光伏电站由于补偿设备的支撑,恢复速度较快,特别是光伏电站恢复速度远高于同步机组。

图3 各发电机组故障时有功响应Fig.3 Active response during failure of each generator set
3.1.2 基于DDE-IPM 法的超平面系数求解
在DIgSILENT/PowerFactory 仿真软件中仿真得到潮流数据,根据DDE-IPM 在超平面的约束条件下,构建安全域的超平面,最后得到最优的超平面系数。设置渗透率为10 个梯度,增加量为5%,起始渗透率为5%,求出10 组超平面系数,计算结果见表1。
表1 中超平面系数的绝对值大小代表了G89 传统同步机组、风电机组、光伏电站的有功注入点对系统稳定性影响的程度。可以看出,传统机组的出力变化对系统的影响最大,但随着渗透率的上升,风力机组和光伏电站的影响程度逐渐增加,风电的影响程度始终大于光伏。拟合的超平面方程系数在各渗透率下的求解误差都在1%以内,满足工程上的精度要求。

表1 拟合超平面方程系数Table 1 Fitting hyperplane equation coefficients
3.2 不同渗透率下系统动态安全域
3.2.1 系统三维DNEP-DSR 拟合
经过大量仿真计算发现,DNEP-DSR的边界可用超平面进行拟合,再选取边界附近的若干运行点进行时域仿真,对构建的DNEP-DSR 边界进行检验,其误差可维持在工程允许范围内。其中,渗透率为5%与50%(即渗透率最大与最小情况)的三维动态安全域如图4 和图5 所示,其余渗透率下的DNEP-DSR见附图B1—B8。

图4 5%渗透率下的DNEP-DSRFig.4 DNEP-DSR at 5% penetration rate
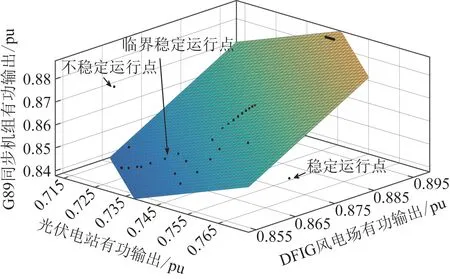
图5 50%渗透率下的DNEP-DSRFig.5 DNEP-DSR at 50% penetration rate
进一步取DNEP-DSR 边界附近的若干运行点进行时域仿真,根据仿真结果是否暂态稳定以及该运行点是否位于安全域内,来判断该动态安全域边界的准确性。渗透率为5%时运行点的有功功率注入和时域仿真结果见表2 所示。
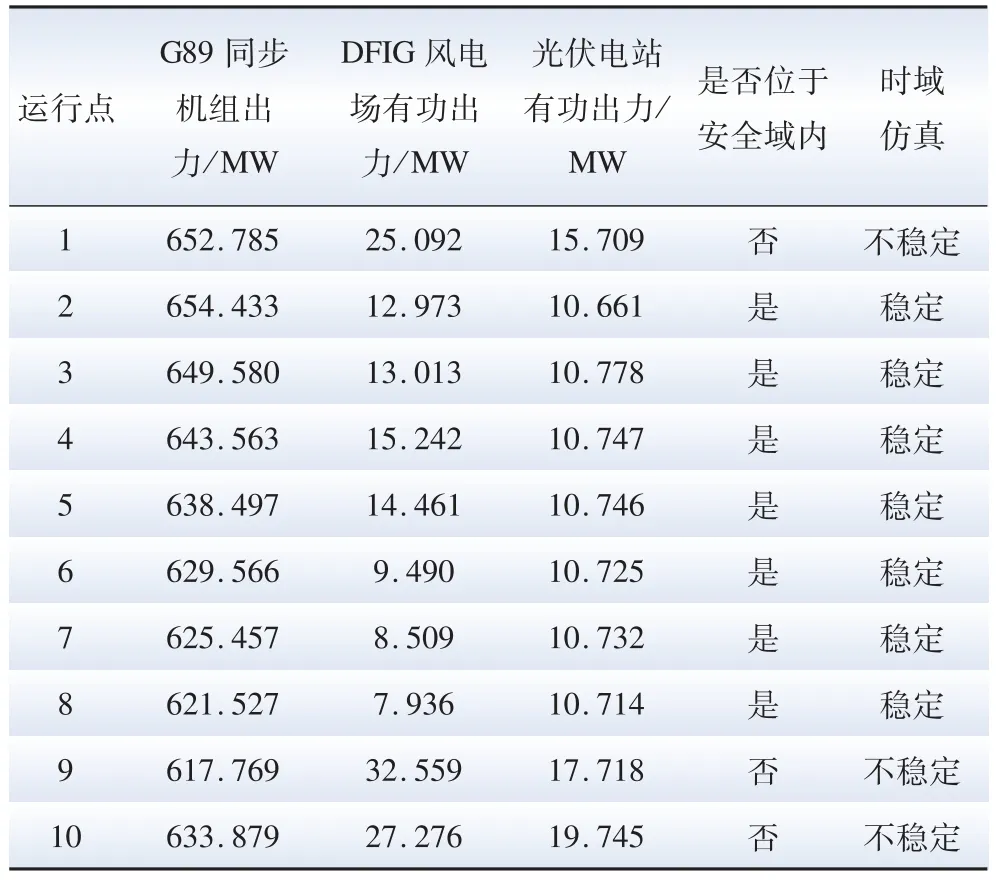
表2 5%渗透率的时域仿真结果Table 2 Time domain simulation results for 5%penetration rate
表2 中,在计算条件相同的情况下,5%的渗透率下的时域仿真在运行点1、9、10(图4 中三维DNEPDSR 域外的运行点)的情况下出现不稳定状态,运行点位于DNEP-DSR 超平面外,不满足暂态稳定约束条件。不同新能源渗透率下的系统运行指标对比见表3。
由表3 可以看出,随着新能源接入比例的增加,在时域仿真稳定区域内的运行点增多,表明安全域的边界在外扩,仿真收敛运行速度也在加快,对于预想故障后的供电恢复速度时间也在减少,恢复速度也随之变快。不同构建动态安全域方法的结果比较见表4。

表4 不同构建动态安全域方法的结果比较Table 4 Comparison of the results of different methods of constructing dynamic security regions
由表4 可以看出,采用DDE-IPM 和DDE 构建系统的动态安全域,DDE-IPM 求解超平面系数的误差、求解速度优于DDE,构建超平面的临界点搜索速度也明显优于DDE。
3.2.2 不同渗透率下低电压穿越能力分析
新能源并网具有波动性和间歇性,在构建不同新能源渗透率的动态安全域时,必须考虑其并网的可靠性,才能得到准确的DSR,而最重要的并网指标是其低电压穿越能力[22-23]。实现低电压穿越的关键在于电网故障下新能源机组能不间断地稳定运行,由于在不同渗透率下双馈机组风电场和光伏电站的低电压穿越能力不相同,进而对2 种能源形式在不同渗透率情况下的低电压穿越能力展开研究,在改进IEEE 118 节点测试系统进行时域仿真,仿真结果如图6—9 所示。

图6 不同渗透率下DFIG 风电场故障电压跌落曲线Fig.6 Fault voltage dip curves for DFIG wind farms with different penetration rate

图7 不同渗透率下DFIG 风电场低电压穿越能力Fig.7 LVRT capability of DFIG wind farms with different penetration rate

图8 不同渗透率下光伏电站故障电压跌落曲线Fig.8 Fault voltage dip curves for PV plants with different penetration rate

图9 不同渗透率下光伏电站低电压穿越能力Fig.9 LVRT capability of PV plants with different penetration rate
由图6、7 可以看出,不同新能源渗透率下风电场在故障后电压跌落曲线有所不同,在渗透率较低的情况下,风电场并网低电压穿越的最低点电压要低于渗透率较高的时候,但在故障切除以后,渗透率低的风电场并网点电压的恢复波动范围较小,恢复电压的平稳性要优于渗透率较高的情况。
由图8、9 可以看出,不同新能源渗透率下光伏电站低电压穿越能力有所差异,其变化趋势和风电机组的并网点电压基本相同,在渗透率较低的情况下,光伏电站并网低电压穿越的最低点电压要低于渗透率较高的时候,在故障切除以后,渗透率低的恢复电压平稳性要优于渗透率较高的情况。在构建DNEPDSR 时,测试系统中风电机组和光伏电站均满足并网运行的低电压穿越能力。
4 结论
本文采用DDE-IPM 方法来构建不同新能源渗透率下的电力系统动态安全域,进而分析其对电力系统暂态稳定的影响。通过对测试系统进行大量时域仿真发现,DNEP-DSR 边界可采用超平面法进行拟合,还具有光滑线性特性,且拟合误差在工程允许范围内。通过对基于DDE-IPM 构建的系统动态安全域进行分析,得到以下结论:
通过对比不同新能源渗透率下的电力系统动态安全域,DNEP-DSR 三维动态安全域有近似平行的性质,随着新能源渗透率的增加,安全域边界决定因素向新能源靠近;由于新能源机组的故障响应特性较好,系统的DNEP-DSR 有所扩大,稳定运行点也相应增加。在低渗透率动态安全域中,同步机组占据主要因素,但随着新能源渗透率的增加,风电和光伏的有功出力裕度也将提升,同步机组的有功出力裕度有所减少。研究结果与利用超平面系数来分析3 个独立变量的影响因子相符合,验证了算例的准确性。所提方法可有效增强电力系统动态安全性预测能力,促进电力系统安全在线评估与控制。
附录A

图A1 改进IEEE118 节点测试系统接线Fig.A1 Improved IEEE 118 node test system wiring diagram
附录B

图B1 10%渗透率下的DNEP-DSRFig.B1 DNEP-DSR at 10% permeability rate
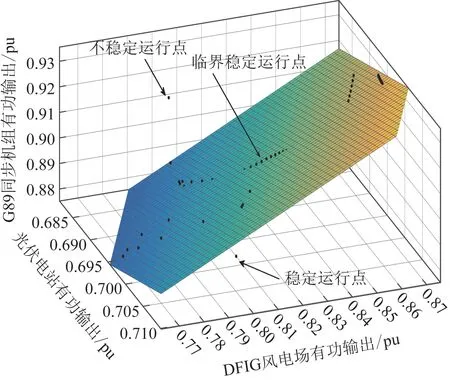
图B2 15%渗透率下的DNEP-DSRFig.B2 DNEP-DSR at 15% permeability rate

图B3 20%渗透率下的DNEP-DSRFig.B3 DNEP-DSR at 20% permeability rate

图B4 25%渗透率下的DNEP-DSRFig.B4 DNEP-DSR at 25% permeability rate

图B5 30%渗透率下的DNEP-DSRFig.B5 DNEP-DSR at 30% permeability rate
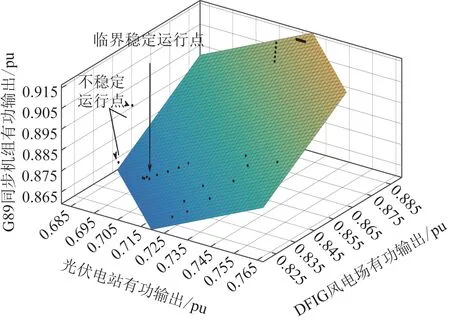
图B6 35%渗透率下的DNEP-DSRFig.B6 DNEP-DSR at 35% permeability rate

图B7 40%渗透率下的DNEP-DSRFig.B7 DNEP-DSR at 40% permeability rate

图B8 45%渗透率下的DNEP-DSRFig.B8 DNEP-DSR at 45% permeability rate

