基于MMC的PET 中间隔离级DC-DC变换器的新型模型预测控制策略

蒋谦，黄志豪，程启明，赵淼圳，傅文倩

(1.华东送变电工程有限公司,上海市 201803;2.上海市电站自动化技术重点实验室(上海电力大学自动化工程学院),上海市 200090)

0 引言

随着风、光、储等新能源的快速发展,大量分布式电源(distributed generation,DG)的接入对电网的安全稳定运行、电能质量以及谐波治理提出了较为严峻的考验。同时电网有限的消纳能力已经成为限制DG 快速发展的主要因素之一[1]。由于DG 受环境、气候的影响较大,输出的功率具有较大的随机性和波动性,通常需要一个具有电流隔离的双向转换器来控制DG与电网之间的功率流[2],采用双有源全桥(dual active bridge,DAB)变流器的三级结构电力电子变压器(power electronic transformer,PET)因其具有功率双向可控的特性,已成为DG 提供智能化接口的有效解决方案[3]。三级结构的PET 不仅可为太阳能、风电等DG 提供交、直流接口,可以实现多端口电能管理、智能电网电能调度控制等功能[4],还具有电压变换、无功补偿和电气隔离等优势[5]。

电力电子变压器也称固态变压器(solid-state transformer,SST),作为智能电网中重要的组成部分,其中间隔离级的DAB DC-DC 变换器的性能在一定程度上会直接影响PET的传输性能[6]。文献[7]采用了基于双H 全桥背靠背式DAB的三级式PET 拓扑,由于PET 中间隔离级采用传统的DAB 结构,并不能满足高电压、大功率的电能传输需求。文献[8]为了解决传统的三级式PET 中间隔离级DAB 中开关管应力过大、传输功率较小和可靠性差等问题,采用了由N个结构相同的DC-DC 变换器串联输入并联输出的中间隔离级DAB 拓扑,但该DAB 拓扑须采用的DC-DC 变换器个数应与高电压等级的输电要求相适应,可扩展性和适应性较差。文献[9-10]设计了基于单臂模块化多电平的中间隔离级DAB 拓扑,该拓扑仅DAB 单侧采用了单臂模块化多电平换流器(modular multilevel converter,MMC),另一侧仍采用传统的单相两电平全桥换流器,因此该拓扑仅适用于配电侧等单侧电压等级较低的电能变换,适用范围较小,同时供电可靠性较低。文献[11-12]提出了基于MMC的隔离型双向DC-DC 换流器,将单相MMC 技术应用于隔离变压器的双侧变流器,扩大了该拓扑的应用范围,但仅采用单个隔离变压器进行电压变换,在隔离变压器检修时并不具备不间断供电能力。文献[13]采用了传统的DAB 拓扑结构,并采用单移相控制,通过调节相移角来控制平均传递功率,但该算法仅可调节一个自由度,且存在较大的电压纹波和开关损耗。文献[14-15]提出了基于传统的DAB 双重移相控制,在两侧H 全桥内引入桥臂内移相,该策略有效地减小了电流应力和电压纹波。文献[16-17]针对基于MMC的双向DC-DC 变换器,提出了一种双PID 控制器的解耦控制策略,对双端MMC变流器设计了基于PID的解耦控制器,但是该策略须先解耦再用多个PID 控制器,控制系统结构复杂,且多个PID 控制器的参数整定困难,特别是PID 这种线性控制方法不太适合于MMC 这种非线性对象控制,因此PID 控制效果并不理想。

模型预测控制(model predictive control,MPC)是一种基于模型的闭环优化控制策略,其可有效地克服过程的不确定性、非线性和并联性,尤其能够方便地处理过程被控变量和操纵变量中的各种约束关系,具有控制效果好、鲁棒性强等优点,因此,近年来模型预测控制已被用于电力电子器件控制中。例如,文献[18-19]提出了一种MPC 策略,能够增强传统DAB的单移相控制算法的灵活性。文献[20]针对MMC提出一种2N+1 电平的直接MPC,提高了输出电压的电平数,降低了交流侧的谐波含量,但是当桥臂子模块数较多时,其每相须预测的开关量也按指数倍增加,控制算法计算量较大。文献[21]针对MMC的MPC 策略提出了分层筛选算法,结合每个控制层的执行顺序,可有效减轻计算负担,并且对每一层使用调整因子,使得调整过程能够高效并适应任何工作条件。但上述针对MMC的MPC 方法都存在价值函数中权重配置难、算法计算量大和实时性差问题。

为解决模型预测控制存在的问题,本文提出一种基于价值函数独立的模型预测控制方法,这种MPC策略将多个控制目标独立计算,无需配置价值函数的权值,避免价值函数的权重配置问题,并减小计算量。另外,针对已有的PET 中间隔离级拓扑存在的问题,设计出基于MMC的新型PET 中间隔离级DC-DC变换器的拓扑结构,该结构采用双高频变压器设计,可有效提高PET 供电可靠性和灵活性。

首先,本文对新型PET 中间隔离级DC-DC 变换器的结构拓扑和工作原理进行分析;其次,根据单相MMC的等效模型,分别构建MMC 交流侧和直流侧的连续域等效数学模型;接着,利用中点欧拉差分方法,分别将MMC 交流侧和直流侧连续域的等效数学模型离散化,并针对MMC 交流侧电流MPC 策略和MMC 环流MPC 策略分别选择价值函数;然后,根据交流侧电流和MMC 环流的价值函数和预测模型构建各自的MPC 控制器;最后,通过实验验证所提方法的有效性和优越性。

1 新型PET 中间隔离级DC-DC 变换器的拓扑结构及数学模型

1.1 拓扑结构

针对现有PET 中间隔离级拓扑存在可靠性较差、适应范围较小等缺点,本文设计出一种基于模块化多电平技术的新型PET 中间隔离级拓扑,其结构如图1 所示。由图1 可见,新型PET 中间隔离级DCDC 变换器由输入、中间、输出3 个部分组成。

图1 MMC-PET 中间隔离级的电路拓扑Fig.1 Topology of MMC-based PET isolation stage

1)输入侧。由2 个单臂单相MMC 变流器将PET 输入级输出的直流电逆变成高频交流电,输入侧所采用模块化多电平技术具有功耗低、适用范围广、电磁兼容性好、可扩展性强等优点,能有效提高变流器的可靠性和经济性。

2)中间隔离级。2 个单臂单相MMC 变流器分别与2 个高频变压器(high frequency transformer,HFT)一次侧一端连接,另一端接地。HFT 将中间隔离级输入侧输出的高频交流电进行电压等级变换。

3)输出侧。由2 个单臂单相MMC 变流器将经过HFT 电压等级变换后的高频交流电整流成直流电。2 个单臂单相MMC 变流器分别与2 个HFT的二次侧一端连接,同时HFT 二次侧另一端接地。

单臂单相MMC 变流器由N个子模块与桥臂电感L和桥臂电阻R相互串联构成,每个子模块(sub module,SM)均采用半桥结构,包含2 个并联反馈二极管的开关管和一个储能电容。通过调整半桥子模块中上下2 个开关器件S1、S2的开通和关断,可实现子模块的投入和切除。当子模块开关管S1开通,S2关断时,子模块输出电压为电容电压。当子模块开关管S2开通,S1关断时,此时子模块的输出电压为0。

本文设计的PET 中间隔离级DC-DC 变换器拓扑采用了2 台HFT,共有2 种运行方式:

1)2 台HFT 同时投入运行的双变压器运行方式,双变压器互为备用。该运行方式与普通采用单HFT的三级式PET 中间隔离级相比,传输的容量更大,当1 台HFT 发生故障时,仍具有不间断供电的能力,供电更为可靠。

2)单台HFT 投入运行的单变压器运行方式。另一台HFT 可作为备用的变压器,在一台需要检修时,将备用变压器投入运行,以提高供电的持续性和可靠性。

综上所述,本文设计的新型PET 中间隔离级DC-DC 变换器的拓扑结构具有较高的调度方便性和灵活可靠性。在正常运行时,可较为方便地改变运行方式以适应传输电能的要求。在一台HFT 发生故障或按计划进行检修时,具有不间断供电或短时停电即可恢复供电的能力,有效地提高了供电的可靠性。

1.2 数学模型

由于新型PET 中间隔离级DC-DC 变换器的隔离变压器左右两侧均采用相同的单臂MMC,因此本文仅选取一侧的单臂单相MMC 进行分析。图2 为新型PET 中间隔离级DC-DC 变换器单侧的单臂单相MMC 等效电路。

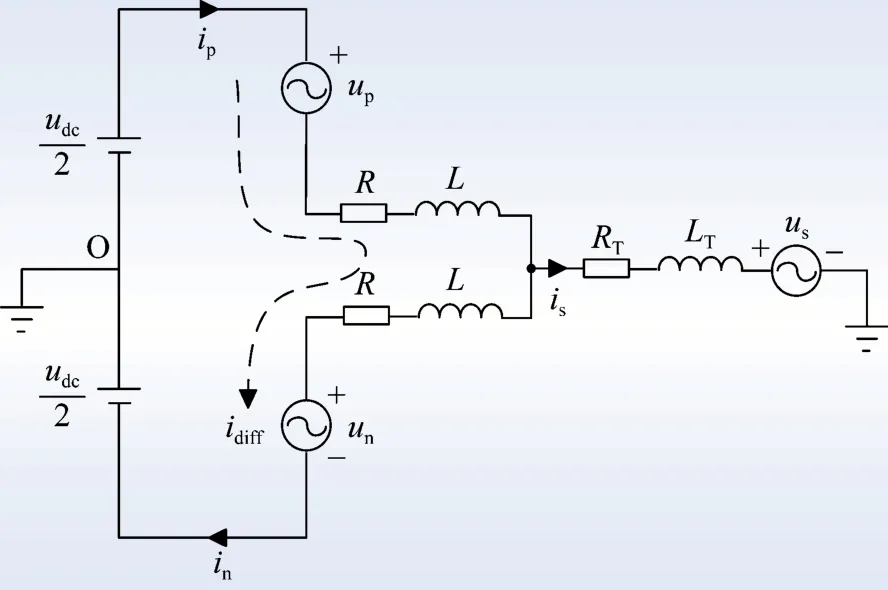
图2 新型PET 中间隔离级DC-DC 变换器单侧的单相等效电路Fig.2 Single-phase equivalent circuit of one side of novel DC-DC converter in the intermediate isolation stage of PET

图2 中:L、R分别为MMC的桥臂电感和桥臂电阻;LT、RT分别为新型PET 中间隔离级DC-DC 变换器的隔离变压器交流侧的等效电感和等效电阻;udc为直流侧输入的直流电压;ip、in分别为MMC 上桥臂电流和下桥臂电流;up、un分别为上下桥臂投入子模块电压之和;is为交流侧输出电流;us为交流侧电压;idiff为MMC 桥臂环流。

根据图2的拓扑和Kirchhoff 定律,可得DC-DC变换器单侧的单臂单相MMC的数学模型为:

将式(1)与式(2)相加可得单臂单相MMC 交流侧等效数学模型为:

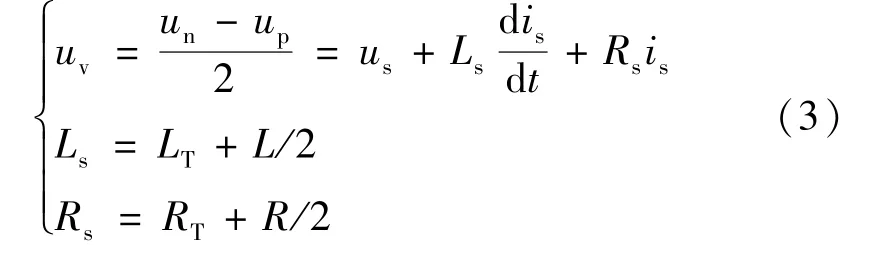
式中:uv为MMC 交流侧输出端相对直流电中性点O的电压。

同理,将式(1)与式(2)相减可得单臂单相MMC直流侧等效数学模型为:

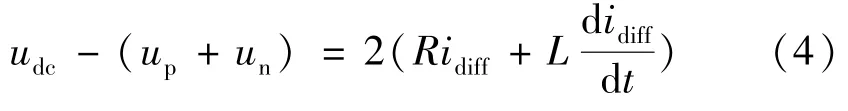
其中,单臂单相MMC 桥臂环流为:

式中:idc为直流侧电流;iz为桥臂环流谐波分量。

2 基于有限控制集MPC 控制策略

2.1 基于有限控制集的MPC 控制系统结构

MPC 由Richalet J 等提出,其特点为:1)对模型的精度要求不高,建模方便;2)采用非最小化描述的模型,系统鲁棒性、稳定性较好;3)采用滚动优化策略,而非全局一次优化,能及时弥补由于模型失配、畸变、干扰等因素引起的不确定性,动态性能较好;4)易将算法推广到有约束、大迟延、非最小相位、非线性等实际过程,尤其能够有效地处理多变量、有约束的问题。因此,MPC 已在工业过程控制中得到了广泛的应用[21]。

变流器的MPC 一般分为传统的连续状态MPC和有限控制集MPC(finite control set-MPC,FCSMPC)两种[20]。由于换流器开关状态的数量是有限的,FCS-MPC 可以将预测控制的优化问题简化为对换流器有限数量的开关状态的优化问题,并适应于变流器的离散特性,具有较高的灵活性和稳定性,因此本文采用FCS-MPC。

FCS-MPC 控制系统的基本结构如图3 所示。由图3 可见,MPC 策略主要分为预测模型、滚动优化和反馈校正3 个部分。

图3 FCS-MPC 控制系统的结构Fig.3 Structure of FCS-MPC control system

图3 中:x*(k+1)为k+1 时刻被控变量x的参考值;g为系统所选取的价值函数值;g(i)为第i个开关状态下价值函数值;S为通过滚动优化筛选出的最优的开关状态;x(k)为k时刻被控变量x的采样值;x(k+1)为经过预测模型进行被控变量预测的预测值。

2.2 模型预测控制器设计

由于MMC 存在电容电压不平衡和环流等问题,因此,MMC的MPC 方法需要采用一个价值函数来解决交流侧电流控制和循环电流控制等问题。但是,一般的MPC 方法都需要配置价值函数的权重,并且由于MMC 各桥臂数目多,因而切换状态多,计算时间长。为了解决这些问题,本文提出了一种无须配置价值函数的权重且减少状态数的MPC 方法——基于价值函数独立的MPC 控制方法,用于MMC的交流侧电流控制和循环电流控制。该方法由2 个MPC 组成,每个价值函数针对不同的控制目标进行设计,其中:第1 个价值函数仅控制交流侧电流;第2 个价值本函数仅控制循环电流。本文所提的控制方法不但无须配置价值函数的权重,而且减少了每个价值函数中所需的状态,从而使MMC 精确平稳运行。下面详细讨论2 个MPC的设计过程。

2.2.1 MMC 交流侧电流的MPC 策略

为了实现对交流侧输出电流is的预测,需要将MMC 连续域的数学模型式(3)进行离散化处理。由于离散化后预测模型的准确性直接决定了MPC 系统的准确性[21],对于多控制目标的MMC 系统而言,预测模型的准确性尤为重要,因此本文采用中点欧拉法[3]。

由式(3)可得被控量的微分方程为:

式中:u、x分别代表MMC 系统的输入量、控制量。

中点欧拉法的表达式为:

式中:Ts为采样周期。

根据式(7)将MMC 连续域的数学模型式(3)进行离散化处理,可得:

式中:is(k)、is(k+1)分别为k、k+1 时刻交流侧电流;uv(k)、uv(k+1)分别为k、k+1 时刻MMC 交流侧输出端相对直流电中性点O的电压;us(k)、us(k+1)分别为k、k+1 时刻交流侧电压;A=

由于采样周期Ts较小,可认为在1 个Ts内,us(k+1)=us(k),可得简化后交流侧输出电流的预测模型为:

MPC 通过定义一个价值函数,使得输出的交流电流紧紧跟随其参考值。本文选取交流侧电流MPC的价值函数gs为:

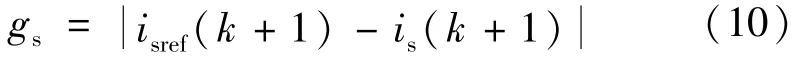
式中:isref(k+1)为交流侧电流的跟踪参考值。

定义子模块的开关函数为:

式中:Si为第i个子模块的开关函数,i=1,2,…,N-1,N。

令N为MMC 上下各桥臂的子模块个数,假设每个子模块电容电压一直为udc/N,则MMC 输出的电压参考值为:

式中:up(k+1)、un(k+1)分别为k+1 时刻MMC的上桥臂、下桥臂电压值;Spi、Sni分别为MMC的上桥臂、下桥臂第i个子模块的开关函数。

由于MMC的上、下桥臂各投入的子模块数为N,因此MMC 上、下桥臂投入的子模块数共有N+1种投切组合,分别为({0,N},{1,N-1},…,{N-1,1},{N,0})。因此,根据式(12),MMC 交流侧输出端相对直流电中性点O的电压的预测值uv(k+1)可表示为:

MMC 交流侧电流的MPC 策略实现流程如图4 所示。首先,由于MMC的输出电压不能跃变,可预测下一个采样周期有限个可能的开关状态;其次,再根据每一种开关状态,预测下一个采样周期的交流侧电流is(k+1)的值;然后,计算出每一种开关状态所对应的价值函数值;最后,通过滚动优化,得出有限个开关状态中价值函数值最小的开关状态。

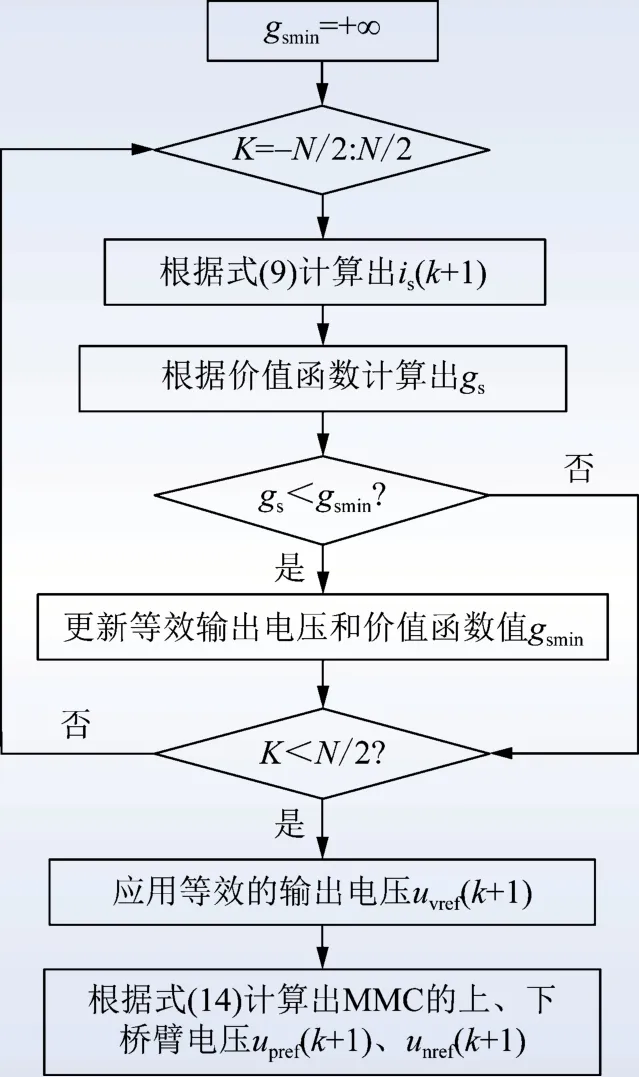
图4 MMC 交流侧电流的MPC 策略Fig.4 MPC strategy of current on MMC alternating side

经过MPC 滚动优化后,根据新型PET 中间隔离级DC-DC 变换器单侧的单相等效电路,MMC 在k+1 时刻上、下桥臂的电压值可表示为:

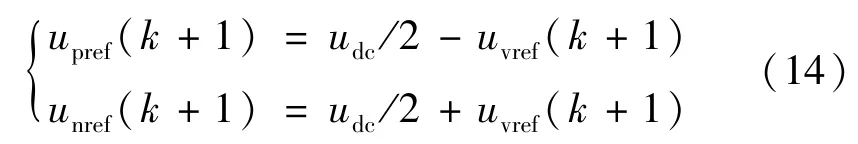
式中:uvref(k+1)为最优开关状态所对应的k+1 时刻MMC 交流侧输出端相对直流电中性点O的电压;upref(k+1)、unref(k+1)分别为最优开关状态所对应的k+1 时刻MMC 变流器的上、下桥臂电压。

2.2.2 MMC 环流的MPC 策略

由于子模块电容电压实际值与理论值存在差异,因此在MMC的内部会形成环流。由式(3)可知,环流的大小与MMC的外部输出特性无关,但是环流的存在将会导致系统损耗的增加,并加大子模块电容电压波动。由于MMC的固有特性,环流并不能完全消除,但需要对环流进行有效地抑制,以减小系统运行的成本,提高器件的运行寿命。

根据式(7),将式(4)利用中点欧拉差分的方法,可得MMC 直流侧在离散域的等效数学模型为:

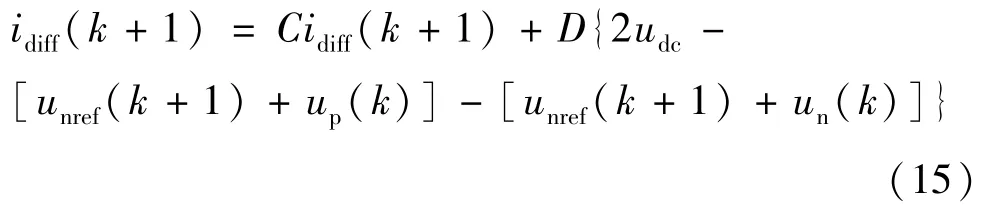
式中:udc为直流侧电压;idiff(k+1)为k+1 时刻MMC 桥臂环流;C=。

根据式(3)可以看出,由于MMC 交流侧输出端相对直流电中性点O的电压uv仅代表MMC 上、下桥臂输出电压的差值,并不能控制相间环流,因此分别在上、下桥臂添加补偿电压udiff,来达到控制环流的目的。式(15)改写为:

假设MMC 上、下桥臂插入一个想用的补偿电压udiff,则udiff共有3 个状态,即为:

本文选取的环流MPC 价值函数gd为:

式中:izref(k+1)为k+1 时刻MMC 桥臂环流的参考值。

为了抑制MMC的桥臂环流,令桥臂环流的参考值izref(k+1)为0,根据式(5)可将选取的环流MPC价值函数式(18)变为:

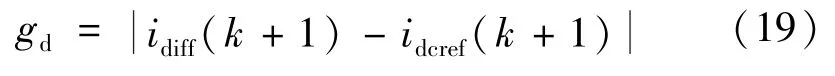
式中:idcref(k+1)为直流侧电流的参考值。

图5 为MMC 环流的MPC 策略实现的流程。首先,确定补偿电压udiff有限个状态数;其次,根据udiff的每个状态数,预测出下一个采样周期内部电流的idiff值;然后,根据环流的MPC 价值函数计算出每一种开关状态所对应的价值函数值;最后,通过滚动优化,得出有限个状态数中价值函数最小的补偿电压值。最终上、下桥臂的参考电压为:

图5 MMC 环流的MPC 策略实现的流程Fig.5 Flow chart of MPC strategy implementation for MMC circulating current

根据MMC 上、下桥臂最终的电压参考值可得上、下桥臂在k+1 时刻所投入的模块数,并采用电容电压排序的方法,进行电容均压控制。

3 实验结果分析

为了验证本文所提基于价值函数独立的MPC 方法的有效性和优越性,搭建了图1 所示的基于MMC的新型PET 中间隔离级DC-DC 变换器的实验平台,并把本文所提的MPC与常用的PID 控制进行实验比较。本文所提新型DC-DC 变换器系统参数见表1。

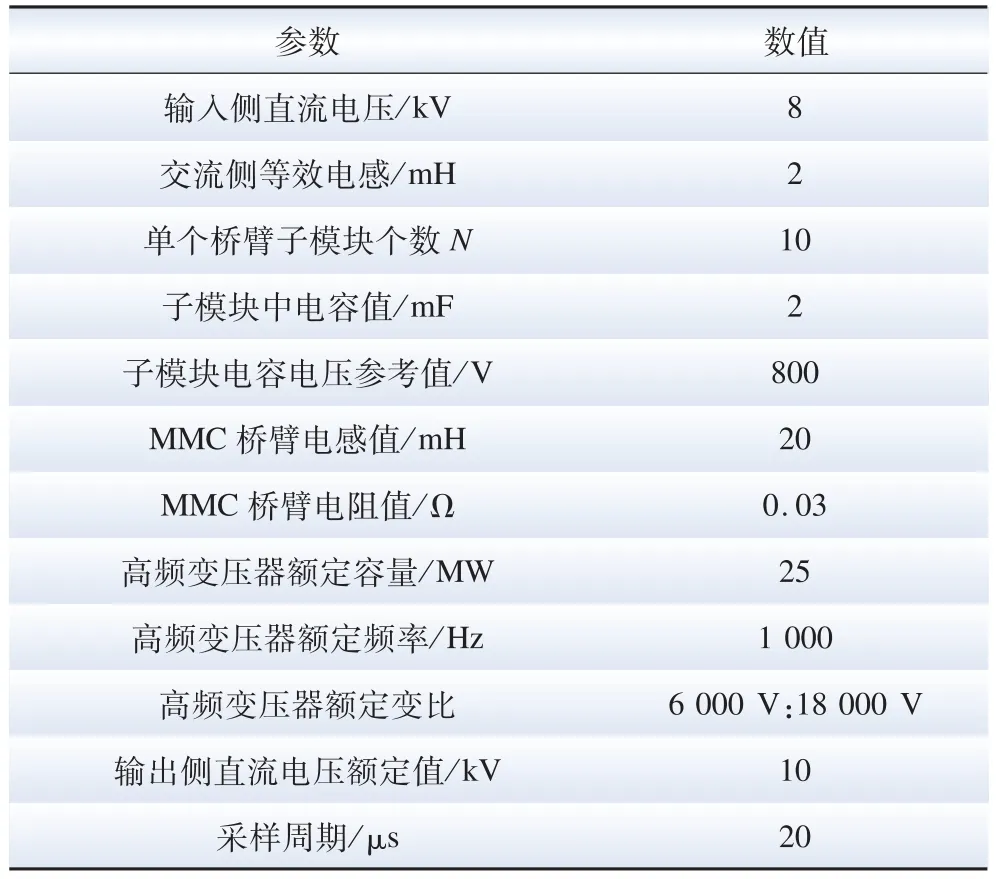
表1 新型DC-DC 变换器的系统参数Table 1 System parameters of the novel DC-DC converter

1)逆变侧交流电压指令发生变化。

在t=0.50 s 时,PET 中间隔离级DC-DC 变换器逆变级2 个单臂模块化多电平的交流电压指令值从1.0 pu(6 000 V)阶跃变化到1.8 pu,系统的响应如图6 所示。其中:图6(a)、(b)为采用本文所提MPC、常用PID 控制的新型PET 中间隔离级DC-DC变换器逆变侧的输出电压;图6(c)、(d)为采用本文所提MPC的新型PET 中间隔离级DC-DC 变换器逆变侧的输出电流、MMC 子模块的电容电压;图6(e)、(f)为采用本文所提MPC、常用PID 控制的新型PET中间隔离级DC-DC 变换器逆变侧的MMC 内部环流。

图6 逆变侧交流电压指令变化时系统响应曲线Fig.6 System response curve when AC voltage command changes on the inverter side

图6(a)和图6(b)表明,在t=0.50 s,逆变侧交流指令值发生变化时,采用本文所提MPC的新型PET 中间隔离级DC-DC 变换器与采用常用PID 控制器的新型PET 中间隔离级DC-DC 变换器相比,交流侧电压能够快速达到指令值附近,暂态响应速度较快(调节时间小于2 个逆变侧输出交流电压额定频率周期);从图6(c)和图6(d)可以看出,新型PET 中间隔离级DC-DC 变换器输出电流紧紧跟随指令值,同时逆变侧的子模块电容电压在交流侧指令值发生变化时,并未产生较大的波动;图6(e)和图6(f)表明,在逆变侧交流指令值发生变化时,采用本文所提MPC的新型PET 中间隔离级DC-DC 变换器的MMC 环流被抑制在±5 A 附近波动,其效果比采用常用PID 控制的新型PET 中间隔离级DC-DC 变换器的MMC 抑制环流效果更为明显。

2)整流侧直流电压指令发生变化。

在t=0.50 s 时,PET 中间隔离级DC-DC 变换器整流级2 个单臂模块化多电平的直流电压指令值从1.0 pu(10 kV)阶跃变化到1.2 pu,系统的响应如图7 所示。其中:图7(a)、(b)为采用本文所提MPC、常用PID 控制的新型PET 中间隔离级DC-DC 变换器逆变侧的输出电压;图7(c)、(d)为采用本文所提MPC的DC-DC 变换器逆变侧的输出电流、MMC 子模块的电容电压;图7(e)、(f)为采用本文所提MPC、常用PID 控制的DC-DC 变换器逆变侧的MMC 内部环流。

图7 整流侧直流电压指令变化时系统响应曲线Fig.7 System response curve when DC voltage command changes on the rectifier side

由图7(a)和图7(b)表明,在t=0.50 s 时,整流侧直流电压指令发生变化,与采用常用PID 控制器的DC-DC 变换器相比,采用本文所提MPC的DCDC 变换器响应速度相对较快,直流电压能够在0.12 s内达到指令值附近;由图7(c)和图7(d)可以看出,在整流侧直流电压指令发生变化时,DC-DC 变换器的输出电流和子模块电容电压均未发生较大的波动,但图7(d)中电容电压出现小幅振荡,其由于在整流侧的指令值突然变换,对本文采用的双代价函数的函数值影响较大,为DAB 整流侧的直流值快速达到指令值,需要对MMC 电容进行快速充电,而抑制MMC 环流的MPC 控制器需要抑制环流的突然变换,环流大小又与MMC 子模块的电容电压波动具有一定的相关性,需要抑制电容电压的较大波动,这样电容又需要放电,以维持环流在较小的范围内,因此电容电压出现了一定程度的振荡;图7(e)和图7(f)表明,采用本文所提MPC的DC-DC 变换器的MMC环流控制效果比用常用PID 控制的DC-DC 变换器的MMC 环流控制效果更好,且在整流侧直流电压指令发生变化时,环流未产生较大波动。

总之,由图6 及图7 实验曲线分析可见,不管是PET 中间隔离级DC-DC 变换器逆变级MMC的交流电压指令变化,还是整流级MMC的直流电压指令变化,本文所提MPC 策略的快速性、稳定性和鲁棒性等控制指标均优于常用的PID 控制。

4 结论

本文设计了基于MMC的新型PET 中间隔离级DC-DC 变换器拓扑结构,提出了基于独立价值函数MPC的PET 中间隔离级DC-DC 变换器两侧MMC的控制方法。通过理论与实验分析得出以下结论:

1)MPC 省略了电流内环,避免了PID 控制器多且控制参数整定困难问题,同时该控制策略不依赖于DC-DC 变换器精确的系统模型,具有适应性较强的特点。

2)本文所提基于独立价值函数的MPC,无须对价值函数的权重进行配置,减小了MPC 控制器的计算量。

3)本文采用中点欧拉法将DC-DC 变换器的连续域数学模型进行离散化,提高了MPC 控制系统的准确性。

4)新型PET 中间隔离级DC-DC 变换器的MPC与常用的PID 控制相比具有更好的控制性能。