基于VSC与DRU的混合级联型海上风电直流外送系统控制与阻抗建模
王诗超,孙仕达,郝为瀚,张港华,向往,黄阳,区晓良
(1.中国能源建设集团广东省电力设计研究院有限公司,广州市 510663;2.强电磁工程与新技术国家重点实验室(华中科技大学),武汉市 430074)
0 引言
近年来,海上风电柔性直流并网作为实现“双碳”目标的重要途径,呈现规模化、集群化及深远海化的特点[1-2]。基于电压源型换流器(voltage-source converter,VSC)的高压直流输电技术已应用于海内外多个海上风电并网工程,但其存在子模块数量多、质量大、造价昂贵等制约因素[3-4]。针对上述问题,西门子公司及学术界提出了基于二极管整流器(diode rectifier units,DRU)的直流外送方案,但仍存在无功功率需求大、稳定性差、无法黑启动等技术挑战[5]。
为综合两者优势,文献[6]提出了VSC与DRU直流侧串联的混合直流系统,该拓扑具有功率可以控制、可以黑启动等优势,但外送功率受限于全控电力电子器件耐流水平。文献[7]提出了DRU与主动换相型电流源换流器直流侧串联的混合直流系统,实现海上平台轻型化,但该方案需要大容量无功功率和谐波电流补偿元件。文献[8]提出了DRU与辅助VSC直流侧并联的混合型换流器,但该拓扑仍存在体积和质量大问题。为减少VSC 换流器容量,同时实现多落点大容量供电,文献[9]进一步提出了VSC与多个DRU 混合级联方案,通过500 MW的VSC 即可实现2 500 MW 功率传输。
然而,上述文献多关注混合直流输电系统拓扑、运行与控制方面的问题。在海上风电大规模集中并网、装备电力电子化等背景下,并网系统稳定性问题日益突出[10-11],混合换流站的稳定性分析具有重要意义。而基于小信号扰动的dq轴下阻抗建模方法物理意义明确、测量简便,是分析稳定性的重要基础。
目前,海上风电并网系统稳定性研究主要关注单个VSC、DRU 或者电网换相换流器(line-commutated converter,LCC),未有文献对混合级联换流器结构进行分析。由于混合级联输电系统中VSC 和DRU 在直流侧级联,在交流侧并联,其阻抗特性与单个VSC、DRU 阻抗特性截然不同。另一方面,为了建立DRU的交流电压,VSC 需采用电压源型控制策略,且应具备功率-电压主动协调能力。但现有文献多采用定电流控制的并网逆变器阻抗模型,并不适用于电压源控制型VSC 换流器[12-13],且均忽略了功率控制的影响。文献[14]建立了LCC的阻抗模型以分析与弱电网互联下的稳定性问题。此外,现有文献少有研究DRU的阻抗建模,文献[15]在文献[16]基础上建立了较为详细的DRU 阻抗模型,但并未考虑DRU直流滤波电感的影响,影响建模精度。
为解决上述挑战,本文基于VSC与DRU 构成的混合级联型海上风电直流外送系统,对其控制及阻抗建模开展研究。首先建立考虑直流侧滤波电感的VSC-DRU 混合级联换流站的详细数学模型;以实现系统功率分配与电压稳定运行为目标,研究含有源阻尼的VSC 功率-电压调节控制策略;其次,考虑锁相环及功率控制环等受扰动影响,采用小信号扰动方法,推导并分析dq旋转坐标系下闭环控制的VSC、含无源滤波装置的DRU 和VSC-DRU 混合级联换流站的详细阻抗模型。最后通过仿真验证功率-电压调节控制策略以及阻抗模型的正确性。
1 混合级联型海上风电直流外送系统拓扑结构
以正极为例,基于VSC与DRU的混合级联型海上风电直流外送系统的拓扑结构如图1 所示。该外送系统低压阀组采用12 脉波DRU,高压阀组则采用VSC。高低压阀组在交流侧经变压器并联接入至220 kV 交流母线的公共耦合点(point of common coupling,PCC),在直流侧级联构成混合级联型海上风电直流外送系统。
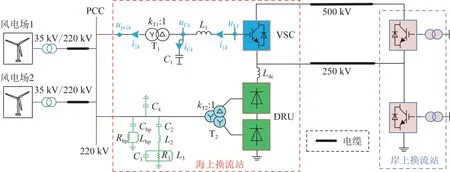
图1 基于VSC与DRU的混合级联型海上风电直流外送系统拓扑Fig.1 Topology of offshore wind power hybrid cascade DC transmission system based on of VSC and DRU
为有效降低谐波污染对系统稳定的影响,海上换流站在VSC 交流出口设计了LC 滤波器,且在220 kV交流母线处配置了无源滤波装置,包含滤波电容、高通滤波器和双调谐滤波器。其中,高通滤波器能在较宽频带上呈现较低阻抗以滤除高次谐波,而双调谐滤波器用于同时消除2 个不同频段的目标谐波[17]。
基于VSC-DRU的混合级联型海上风电直流外送系统能充分利用VSC的高可控性和二极管器件开关损耗小、耐压通流能力强、体积小等优势。且海上换流站高低压阀组的直流侧能够与岸上换流站不同电压等级的高低阀组进行连接,具有较强的运行灵活性。为便于分析,本文研究的混合级联型海上风电直流外送系统的高低压阀组直流侧电压等级分别选为500 kV 和250 kV。
2 VSC-DRU 混合级联换流站数学模型及控制
2.1 VSC-DRU 混合级联换流站数学模型
2.1.1 VSC 数学模型
混合级联型海上风电直流外送系统中VSC 拓扑结构如图1 所示。其中,L1为滤波电感,LT1为变压器T1等效漏感,变压器T1、T2变比为kT1、kT2,C1为滤波电容,uEk、uCk和upcck(k=a、b、c)分别为VSC 换流器交流出口电压、滤波电容电压和PCC 点电压,VSC 换流器的直流侧电压和占空比分别为Udc、d,i1k、iCk、i2k分别为滤波电感电流、滤波电容电流和注入PCC 点电流。为统一系统的建模和分析,上述电气量和电感电容参数均转换至变压器T1的PCC 侧。
基于基尔霍夫电压定律,可得abc 坐标系下VSC换流器交流侧电压电流关系[13],转换至dq旋转坐标系为(以d轴为例):

式中:i1d和i1q、i2d和i2q分别为i1k、i2k的dq轴分量;dd、uCd、uCq、upccd分别为d、uCk、upcck的dq轴分量;ω0为电网额定角频率;s为微分算子。
VSC 换流器从海上风电场外送的有功功率PVSC为:

式中:upccq为upcck的q轴分量;为一阶滤波器的传递函数,G0为其通带增益,ω1为其截止角频率。
2.1.2 DRU 数学模型
考虑DRU 直流侧滤波电感Ldc上的压降作用,建立DRU的详细数学模型。在一个工频周期内,单个DRU 整流的直流电压由重复的6 个电压波段组成,每个电压波段包含上下桥臂中一对二极管导通过程及期间的换相过程。以二极管D5-D6-D1的换相及D6-D1的导通过程为例进行分析,如图2 所示。

图2 从D5 -D6到D6 -D1的DRU 导通模型Fig.2 DRU conduction model from D5 -D6 to D6 -D1
由图2 得DRU的导通电压电流关系为:

式中:udcp、udcn分别为DRU 直流侧正负极电压;Lr为变压器T2等效漏感;Ldc为DRU 直流侧滤波电感;ik(k=a、b、c)为DRU 交流侧电流;Idc为DRU 直流侧电流,其中:

由式(3)整理可得,在dq旋转坐标系下,D5-D6-D1换相过程的直流电压和D6-D1导通过程的直流电压分别表示为[18]:
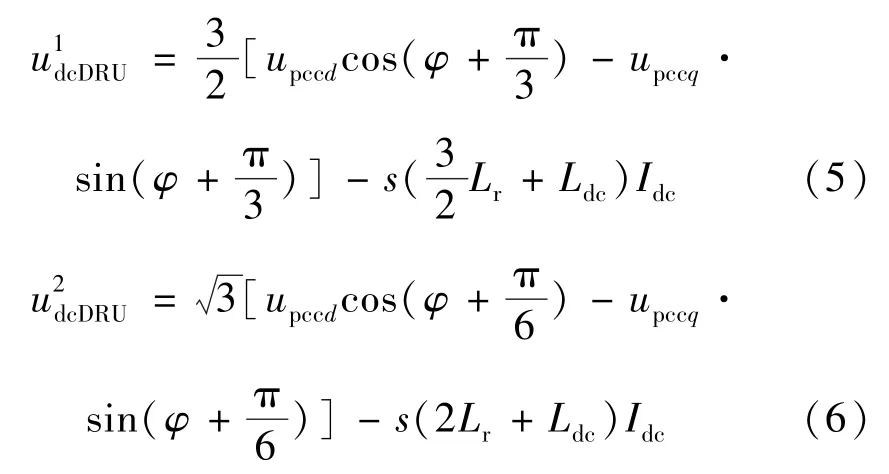
式中:φ为DRU 交流侧的旋转相角。
考虑一个工频周期,DRU 直流电压UdcDRU和有功功率PDRU满足:

式中:Upcck为upcck的幅值。
综上,以PCC 电压upcck为控制量,VSC 和DRU注入PCC 电流i2k、ik为状态量,可得dq旋转坐标下VSC-DRU 混合级联换流站的详细数学模型。
2.2 VSC 换流器控制策略
本文中海上风电机组网侧换流器采用文献[19]的构网(grid-forming)控制以在图1的PCC 自主构造交流电网频率,而海上风电直流外送系统中VSC通过锁相环(phase locked loop,PLL)跟踪PCC 电压相角。岸上换流站高低压阀组均采用定直流电压控制,以保证系统直流电压稳定。
为实现海上风电直流外送功率稳定传输,VSC 自主控制VSC-DRU 混合级联换流站的PCC 电压稳定。由于DRU 不具备控制电压稳定和功率传输的能力,由式(8)所示DRU的有功功率传输特性可知,在直流电压UdcDRU及参数Lr、Ldc固定的情况下,有功功率PDRU与PCC 电压Upcck呈正相关,则DRU 传输的有功功率将是固定的,风电场出力波动要由VSC 承担。
因此,为保证在风电场出力显著上升时不导致VSC 过流,在风电场功率大幅缺额时不引起潮流反转,充分利用DRU 通流能力强的特点,VSC 应具备功率-电压调节控制能力,实现混合级联型海上风电直流外送系统中高低压阀间功率的合理分配。功率控制环如式(9)所示,即由VSC 外送的有功功率PVSC与参考功率Pref的偏差经PI 调节器轻微调整交流电压控制回路的指令值urefd,以实现直流外送系统有功功率在混合级联阀间的主动控制,同时保证PCC 交流电压运行在合理区间。

式中:GPPI为功率控制环的PI 控制传递函数;kPp、kPi分别为比例系数、积分系数。
VSC 设计了模拟滤波电容并联电阻RC的有源阻尼控制策略以抑制谐振尖峰,即通过反馈滤波电容电流iCk,并经有源阻尼反馈增益GRC后添加至调制电压信号中。该控制不仅保持了LC 滤波器对高频谐波的衰减性能,且在正常运行时不会产生高额功率损耗[20],GRC可表示为:

综上,功率控制环产生的PCC 参考电压经电压电流双环PI 控制后生成VSC的调制电压信号,所设计的含有源阻尼的功率-电压调节控制策略具体如图3 所示。
图3 中:i2refd和i2refq为电流内环参考电流i2ref的dq分量;GuPI为电压外环PI 控制器的传递函数,其比例和积分系数为kup和kui,GiPI为电流内环PI 调节器的传递函数,其比例和积分系数为kip和kii;Upccd和Upccq为upcck的dq轴稳态分量;iCd和iCq为iCk的dq轴分量;md和mq为调制电压的dq轴分量;θref为PCC 点电压相角。
图3 中低通滤波器的传递函数GLpass如式(11)所示,ωc为低通滤波器的特征角频率。

图3 VSC 换流器控制策略Fig.3 Control strategy of VSC converter

3 VSC-DRU 混合级联换流站的阻抗建模
3.1 VSC 换流器闭环阻抗模型
在VSC 换流器开环模型的基础上,VSC 换流器小信号闭环阻抗模型需综合考虑控制中PLL、功率控制环和含有源阻尼的电压电流双环控制各部分模块的影响。在本文建模中,变量的上标“^”表示其在小扰动作用下生成的扰动量,在下文各变量出现上标“^”时不再赘述。
1)开环阻抗模型。
对式(1)所示的VSC 添加小信号扰动,忽略直流侧电压Udc的波动,可得dq轴下VSC 开环状态的小信号模型:
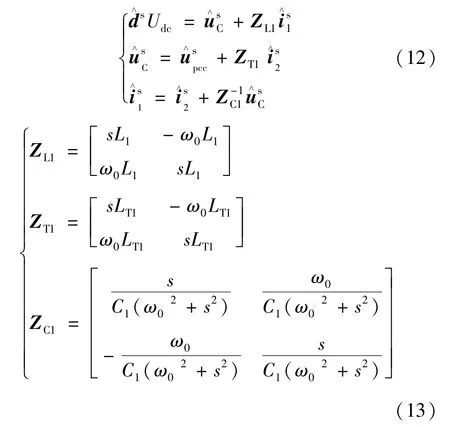
式中:上标s 表示该变量在系统坐标系下;ds为dd和dq的列向量;分别为i1d和i1q、i2d和i2q的列向量;分别为uCd和uCq、upccd和upccq的列向量。
2)PLL 输出相角调节影响。
VSC 通过PLL 跟踪PCC 点电压相角θref,并作为所研究控制器中dq变换参考相角,考虑变压器T1、T2绕组连接方式,其阀侧dq变换参考相角要变换相应角度。
在稳态运行时,控制器的dq坐标系与系统的dq坐标系重合。但当PCC 突加小扰动时,系统和控制器的dq坐标系会产生的相角差[12],如图4 所示,其转换关系如式(14)所示(以逆时针方向为dq旋转正方向):
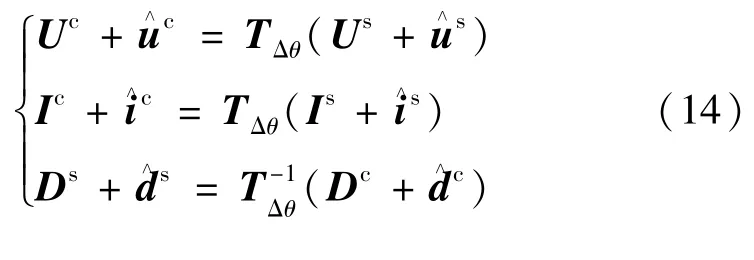
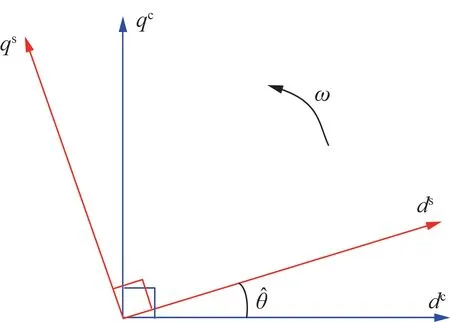
图4 系统和控制器的dq 旋转坐标系Fig.4 d-q rotation axis of system and controller
式中:Uc、Us分别为uc、us的稳态分量;Ic、Is分别为ic、is的稳态分量;Dc、Ds分别为dc、ds的稳态分量;上标s、c 分别表示该变量在系统坐标系和控制器坐标系下;u、i和d分别为电压、电流和占空比的dq轴列向量。
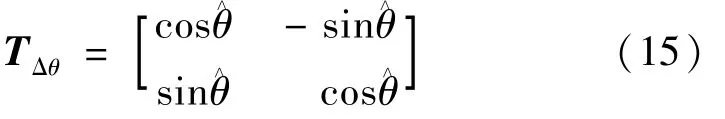
基于式(14),可得PLL 跟踪电压相角变化量的小信号模型为:

式中:GPI为PLL的PI 控制传递函数,其比例系数、积分系数分别为kPLLp、kPLLi。
将式(16)和式(15)代入式(14)中,消去稳态值,以电压u为例,可得PLL 输出相角调节对采样电压影响的小信号模型为:
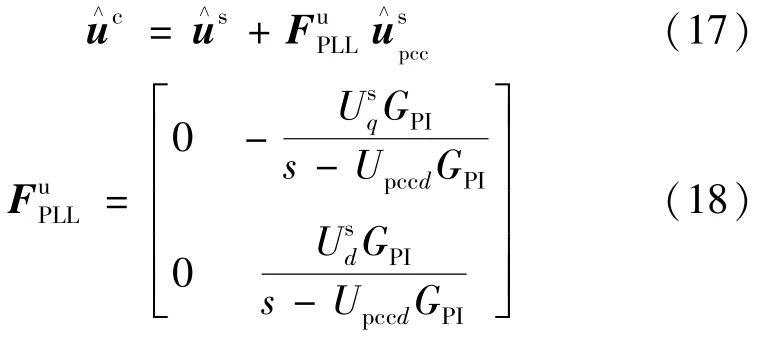
3)功率控制环影响。
式(2)中VSC 从海上风电场外送有功功率PVSC的小信号模型为:

考虑功率控制环中采样电压、电流受PLL 输出相角调节的影响,结合式(19),可求得式(9)所述功率控制环的小信号模型为:

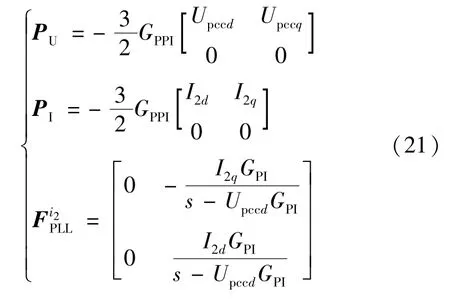
4)含有源阻尼的电压电流双环控制。
图3 所示的VSC 换流器控制策略中,电压电流双环控制的小信号模型可表示为:

由于有源阻尼控制采用变压器T1阀侧的滤波电容电流反馈,在分析闭环小信号模型时,iCk需乘以变压器变比kT1进行等效。有源阻尼控制的小信号模型为:

式中:为在控制器坐标系下的有源阻尼反馈量的dq轴列向量;GRC、kT1分别为GRC、kT1的标量矩阵形式;为系统坐标系下iCk的dq轴列向量。

VSC 换流器传递函数可等效为kPWM,则VSC 换流器交流出口端电压与调制电压信号的关系为:

综上,结合系统开环响应和所研究含有源阻尼的功率-电压调节控制策略,VSC 换流器小信号模型如图5 所示。其中,电气量和阻抗值均转换至变压器T1的PCC 侧。VSC 换流器在含有源阻尼的功率-电压调节控制下,直流外送系统的PCC 电压upcck为控制量,注入PCC 电流i2k为扰动量。基于此,将图5 所示的VSC 换流器闭环小信号模型进行推导化简,得到在dq轴下VSC 换流器闭环阻抗模型ZVSC如下。

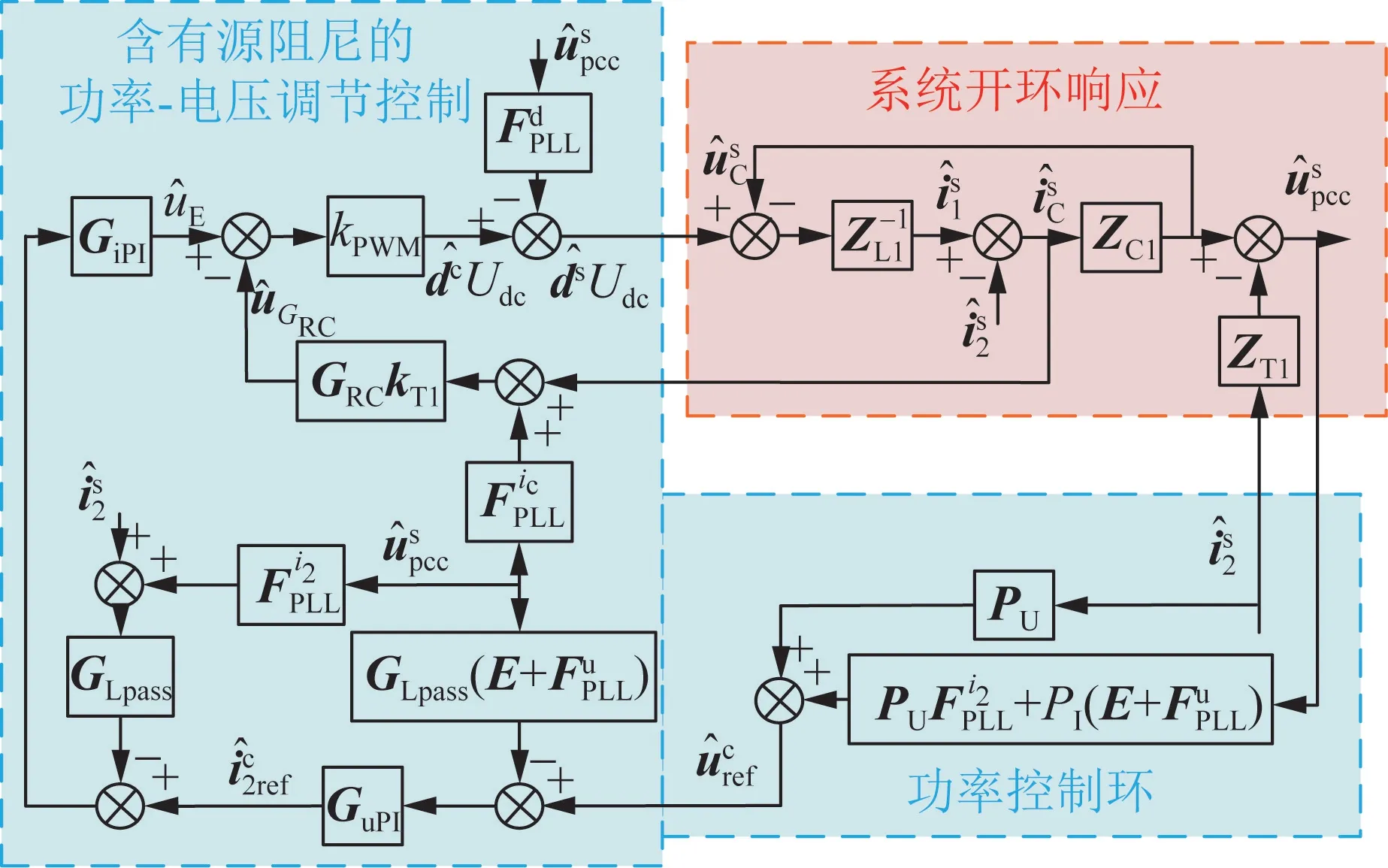
图5 VSC 换流器的闭环小信号模型Fig.5 Closed-loop small-signal model of VSC converter

式中各矩阵的表达式如下:
3.2 DRU 阻抗模型
根据DRU 交流侧等效为电流源和直流侧等效为电压源的特性[21],在dq轴下,DRU 交流侧扰动电压、直流侧扰动电流与交流侧电流、直流侧电压的小信号模型可表示为:
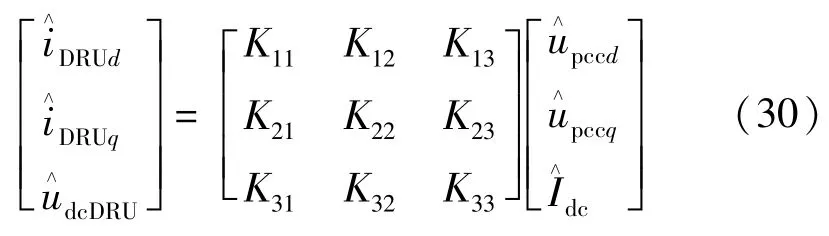
式中:系数Knm(n,m=1、2、3)代表DRU 交流侧和直流侧的电压和电流关系。
DRU 直流侧电压由岸上换流站进行控制,因此在DRU 交流侧施加小扰动时忽略直流侧电压波动影响,即式(30)中为0。DRU 交流侧的电压电流关系可表示为:

式中:ZDRU为DRU 交流侧的阻抗矩阵,其可表示为:
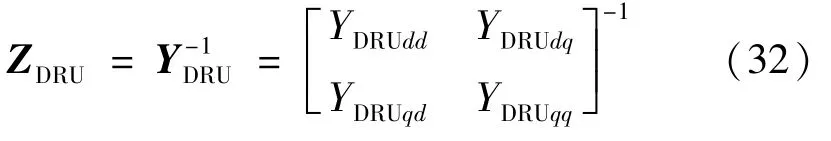
式中:YDRU为导纳矩阵;YDRUdd、YDRUdq、YDRUqd、YDRUq分别为YDRU在dd、dq、qd、qq轴的元素。
结合式(30)和式(31),可求得:

文献[16]对式(33)中系数Knm的求解方法及过程进行了详细分析,本文不再阐述,但文献[16]的数学模型没有考虑DRU 直流侧滤波电感Ldc。因此,本文建立如式(3)所示的DRU 数学模型时对DRU 直流侧滤波电感Ldc进行了分析,使得式(32)的DRU阻抗模型更加详细。
3.3 无源滤波装置阻抗模型
在图1 所示直流外送系统的PCC 配置以滤波电容、高通滤波器和双调谐滤波器组成的无源滤波装置,其阻抗模型ZRLC可表示为:
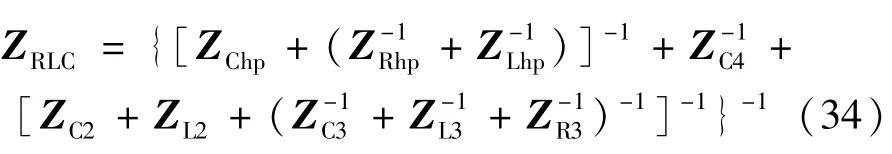
式中:ZC4为滤波电容的阻抗矩阵;ZChp、ZLhp、ZRhp为高通滤波器的阻抗矩阵;ZC2、ZL2、ZC3、ZL3、ZR3为双调谐滤波器的阻抗矩阵;阻抗矩阵均包含dq轴及其耦合分量。
3.4 VSC-DRU 混合级联换流站阻抗模型
混合级联型海上风电直流外送系统中VSC 和DRU 在交流侧并联,在直流侧级联。因此,综合上述各部分阻抗模型,在PCC 侧的VSC-DRU 混合级联换流站闭环阻抗ZS可表示为:
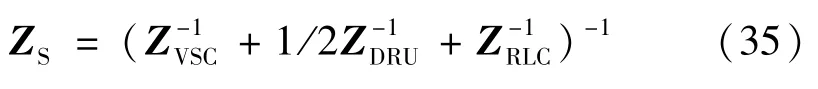
4 仿真验证与阻抗特性分析
为验证本文研究的基于VSC与DRU的混合级联型海上风电直流外送系统控制及其阻抗模型的正确性,采用详细开关器件在PSCAD 软件搭建了如图1 所示的1 500 MW 混合级联型海上风电直流外送系统。其中,VSC 换流器额定容量为500 MW,12 脉波DRU额定容量为1 000 MW,系统仿真参数如表1 所示。
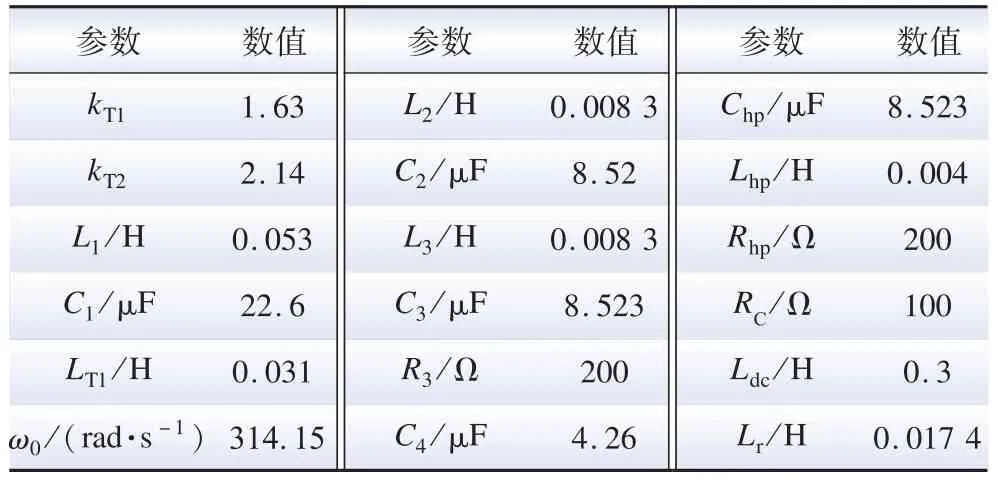
表1 系统仿真参数Table 1 Simulation parameters of the system
4.1 直流外送系统功率波动仿真
图6 为混合级联型海上风电直流外送系统发生功率波动时的仿真波形。海上风电场开始以额定功率运行,向岸上换流站送出功率为1 500 MW,在1.5 s时风电出力发生300 MW 下降,在1.7 s 后恢复为额定功率运行。从图6 可见,在功率-电压调节控制下,VSC 可维持PCC 线电压Upccrms运行在1.04 pu,同时外送500 MW 有功功率;在1.5 s 风电出力下降时,VSC 外送的有功功率PVSC基本保持不变;由于DRU 外送有功功率PDRU下降,由公式(8)可得,PCC电压Upcck会有小幅减小,仿真验证了理论分析的正确性。本文所提控制策略在风机有功出力变化时,VSC 有功功率响应平缓,对系统冲击小。

图6 混合级联型直流外送系统电压和功率波形Fig.6 Voltage and power waveforms of hybrid cascaded DC transmission system
4.2 VSC-DRU 混合级联换流站阻抗模型验证与分析
为验证本文建立的VSC 换流器、含无源滤波器的DRU 及VSC-DRU 混合级联换流站阻抗建模的正确性,阻抗验证方法采用频率扫描方式实现[22],即在图7所示的3 个位置依次添加包含各次谐波频段的小扰动源Δu1、Δu2、Δu3,通过测量图7 中阻抗测量点的各频段电压电流信号,计算该点在各频段的系统阻抗。
1)VSC 换流器闭环阻抗模型。
图8 为在图7 中阻抗测量点1 添加小扰动源时,VSC 换流器闭环阻抗模型的理论分析和仿真测量伯德图,其中,蓝色虚点为传统不考虑功率控制阻抗模型值,红色虚点为本文所建详细阻抗模型值,蓝色圆圈为仿真测量值。
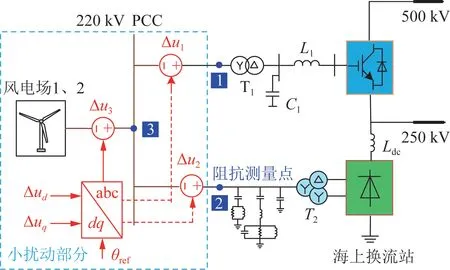
图7 VSC-DRU 混合级联换流站阻抗测量示意图Fig.7 Schematic diagram of impedance measurement of VSC-DRU hybrid cascade station
由图8 可知,ZVSCdd和ZVSCqq在低频段呈现阻容性,而在高频段基本呈感性。通过在VSC 功率-电压调节控制中附加有源阻尼,在中频段(200 Hz)附近,由LC 滤波器谐振导致的阻抗幅值和相位突变被有效抑制。且考虑PLL 和功率控制环的影响,本文所提阻抗模型更加精确,ZVSCdd和ZVSCqq在中低频段不再完全对称,因此,稳定性分析时阻抗模型考虑该因素是必要的。VSC 换流器闭环阻抗模型的理论分析和仿真测量结果一致,验证了本文所建VSC 阻抗模型的正确性。


图8 VSC 换流器闭环阻抗模型对比与验证Fig.8 Comparison and validation for VSC converter closed-loop impedance model
2)含无源滤波装置的DRU 阻抗模型。
图9 为在图7 中阻抗测量点2 添加小扰动源时,含无源滤波装置的DRU 阻抗模型的理论分析和仿真测量伯德图。
由图9 可知,含无源滤波装置的DRU 阻抗模型理论分析和仿真测量结果基本一致,仅在Zdq的低频段存在相位偏高现象,在PSCAD 允许测量误差范围内。所建含无源滤波装置的DRU 阻抗具有在较宽的高频段呈现较低阻抗,且同时消除2 个中高频段目标谐波的特性。验证了本文所建立含无源滤波装置的DRU 阻抗模型正确性。
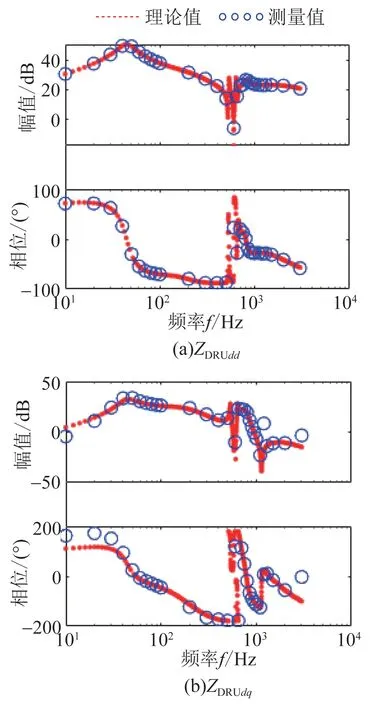

图9 含无源滤波装置的DRU 阻抗模型验证Fig.9 Validation for DRU impedance model with passive filter
3)VSC-DRU 混合级联换流站阻抗模型。
图10 为在图7 中阻抗测量点3 添加小扰动源时,VSC-DRU 混合级联换流站阻抗模型的理论分析和仿真测量伯德图。综合图8、9 和10 可知,ZVSC和ZDRU的中低频段幅值相近,而ZDRU的高频段幅值显著低于ZVSC。由于VSC与DRU 在交流侧并联,Zs中低频段由ZVSC和ZDRU共同决定,Zs高频段主要由ZDRU决定。综上说明了本文所建立的混合级联换流站模型阻抗特性和单个VSC 或DRU 阻抗特性存在较大差异,同时也验证了本文所提控制策略下VSC-DRU 混合级联换流站阻抗模型理论分析和仿真测量结果的一致性和正确性。


图10 VSC-DRU 混合级联换流站阻抗模型验证Fig.10 Validation for impedance model of VSC-DRU Hybrid Cascade Converter Station
5 结语
本文通过研究基于VSC与DRU的混合级联型海上风电直流外送系统的控制设计及其阻抗建模得到结论如下:
1)在dq旋转坐标系下建立了直流外送系统的详细数学模型,通过设计含有源阻尼的VSC 功率-电压调节控制,实现了混合级联直流外送系统有功功率的主动控制,同时保证PCC 交流电压稳定运行在合理区间,仿真验证了在海上风电有功出力波动时混合级联直流外送系统功率的稳定传输。
2)基于所建VSC-DRU 混合级联换流站模型,建立了考虑PLL、功率控制环影响的VSC 换流器闭环阻抗模型,该模型适用于电压控制型VSC,且仿真验证了有源阻尼控制抑制阻抗谐振尖峰的有效性;考虑DRU 直流侧电感作用,建立了含无源滤波装置的DRU 阻抗模型,并分析了该模型对高次特征谐波的良好衰减特性;仿真验证了所建立VSC-DRU 混合级联换流站详细阻抗模型的精度和正确性,为混合级联型海上风电直流系统稳定性的研究工作提供了重要基础。

