宁夏中部干旱带砂土混合覆盖下土壤蒸发估算

贾振江，赵广兴，李王成,2,3，安文举，刘巧玲，李阳阳，徐天渊

(1.宁夏大学土木与水利工程学院，银川 750021；2.宁夏节水灌溉与水资源调控工程技术研究中心，银川 750021；3.旱区现代农业水资源高效利用教育部工程研究中心，银川 750021；4.陕西省水利电力勘测设计研究院，西安 710000)

土壤蒸发不仅是陆地水文循环的重要组成部分，也是农田土壤水分流失的重要途经，尤其在蒸发强烈、降雨稀少的西北旱区，这种无益损耗对农业生产无疑是致命的。因此，摸清土壤蒸发过程并对其进行有效估算对农业生产具有重要意义。完整的土壤蒸发是一个复杂的过程，难以用一个公式对其进行准确的定量表达，在这种情况下，分阶段描述就显得尤为必要。土壤蒸发通常被划分为3个阶段，但在此过程中，蒸发过程受气象条件影响较大，无法准确对此进行有效估算。土水蒸发比为相同外界条件下土壤蒸发量与对应水面蒸发量的比值，在以往对土壤蒸发估算研究中，常常引入土水蒸发比以消除气象因素对土壤蒸发的影响。傅抱璞通过理论分析并依据实际蒸发量和最大蒸发量之比与土壤湿度之间的变化规律，将土壤蒸发过程分为3个阶段，并建立了相关土壤蒸发量计算模型；王积强建立了基于土水蒸发比与其对应土壤含水量的分阶段函数关系；李红星等以水面蒸发量为参考并结合相关微气象参数推求了土壤蒸发量数学模型，进一步简化了土壤蒸发量计算；马己安等基于水面蒸发量和土壤含水量对宁夏中部干旱带地区土壤蒸发过程进行了分段拟合，将裸地蒸发分为3个阶段，压砂地蒸发分为2个阶段。

表土覆砂作为我国西北地区一种传统农业节水技术，具有保温增渗、抗旱抑蒸的功效，但在实际农业生产过程中，伴随耕犁、风化作用及使用年限的增长，土表覆盖物常以砂土混合的形式存在，部分学者对砂土混合覆盖下土壤水分和蒸发特性等方面进行了试验研究，而针对压砂地土壤蒸发模拟及有效估算却鲜有成论；此外，现有土壤蒸发量经验公式大多是在特定地区下获得的，其适用性差异较大。另一方面，众多学者研究表明，土壤蒸发与表层0—1 cm或0—2cm含水量密切相关，如Bittelli等研究发现，0—2 cm土壤水汽通量相比于下层土壤更接近土壤实际蒸发量；李艳等通过研究留茬模式下相对土壤蒸发量与0—2 cm土壤含水量的关系，将蒸发过程划分为2个阶段；孙池涛等基于0—1 cm土壤含水量建立了土壤蒸发阻力模型，并取得良好成效。基于此，本研究拟通过研究6种不同砂土混合比条件下的土水蒸发比与砂土覆盖层下0—1 cm土壤含水量的关系，以此划分蒸发过程，并最终建立适用于本地区的压砂地土壤蒸发经验公式，以期为宁夏中部干旱带砂土混合覆盖下土壤蒸发模拟预测及压砂地生态修复提供理论依据。

1 材料与方法

1.1 试验区概况

于2021年7—8月在宁夏回族自治区中卫市沙坡头区香山乡红圈子村尹东自然队宁夏大学中卫市沙坡头区环香山试验基地(36°56′24″N，105°13′44″E)开展大田试验，该地平均海拔1 760 m。试验区地处宁夏中部干旱地带核心区(36°56′—38°23′N，104°17′—107°39′E)，降雨稀少，多年平均降水量为180～200 mm，且主要集中于6—9月，蒸发强烈，多年平均蒸发量可达2 100～2 400 mm，约为多年平均降水量的10倍。该地区主要地形地貌为平原及山地，独特的地理位置和丰富的砂砾石资源使得砂石覆盖成为当地农业生产的特有耕作模式。

1.2 试验材料

砂土混合物中砂石与土壤的体积之比称为砂土混合比，其中，供试土壤取自研究区自然覆砂的耕作地，试验前在采样区采用“S”形取样法，分别选取10个样点剔除表面20 cm覆层，采集覆层下0—20 cm原状土经自然风干后碾压、磨碎并过1 mm筛。土壤容重为1.37 g/cm，土壤风干含水量(质量)为2.00%，田间持水量(质量)为22.70%，饱和含水量(质量)为34.15%，经Bettersize-2003型激光粒度分析仪测得土壤颗粒粒径为砂粒(1～0.05 mm)占11.80%，粉粒(0.01～0.05 mm)占35.10%，黏粒(0.001～0.01 mm)占31.90%，胶粒(<0.001 mm)占21.10%，采用中国土壤质地分类为壤土。

试验所用砂石取自研究区田间砾石，均为灰绿深灰色板岩，砂石粒径为1～3 cm，试验前分别过1，2，3 cm不锈钢砂石筛，其中，粒径分布在1～2 cm占比约63%，2～3 cm占比约37%，不同粒径砂石在试验前用自来水清洗3遍并晾干备用。

1.3 试验设计

选取地形平整、四周无作物遮挡的荒砂地作为试验场地，采用自制微型蒸渗仪进行大田模拟试验，微型蒸渗仪采用PVC管及其配套构件制成，底部嵌有环套，见图1(a)。其中，内桶内径20 cm，高25 cm，壁厚0.4 cm，外桶内径25 cm，壁厚0.4 cm。外桶以0.5 m间隔等距埋设于地下且高于地面1 cm左右，以防止回漏，且为避免不同处理温湿度的相互干扰，各处理间用厚度为1 cm，高为40 cm的泡沫隔板隔开，同时，在试验区上部安装支架，避免降雨进入蒸渗仪中，布置示意图见图1(b)。

图1 试验装置及布置示意

试验开始前，在蒸渗仪内桶内壁均匀涂抹凡士林以减少边壁效应，然后将筛分好的土样按当地土壤容重1.37 g/cm分层压实装入桶中，每层5 cm，共4层，层间进行打毛，装填完成后静置24 h使桶内土壤达到平衡，之后随即按照砂石和土的体积与容重之积分别计算相应质量，混合均匀后放入桶内并压实，覆盖厚度为4 cm。灌水前在覆盖层表面铺设滤纸，(裸土以土面为基准面，覆砂以砂层表面为基准面)，先后向每个桶中缓慢均匀灌水至覆盖层表面明显有水渗出。同时，在试验场地空旷处同等位置另设内径为20 cm的E601B型标准蒸发皿，水面与各处理基准面齐平，定时补充水分蒸发消耗且与土壤蒸发量同步测量。

本试验共设6个砂土混合比处理，分别为S1(0)、S2(20%)、S3(40%)、S4(60%)、S5(80%)、S6(100%)，每个处理10个重复，其中5个重复用来建模，5个重复用以验证。

1.4 试验流程

试验选取蒸发强烈的7月22日至8月30日进行，直至各处理土水比不再发生变化时结束，共计40天。试验过程中，土壤蒸发量采用称重法测得，所用电子称量程为300 kg，精度为0.01 kg，根据土壤蒸发强度前期每12～24 h测定1次，后期每48～72 h测定1次，测定时间为每天8:00和20:00，由土样质量的变化计算实际蒸发量。

土壤表层质量含水量测定与土壤蒸发强度同步，通过取样孔进行破坏性取样获取砂土覆盖层下0—1 cm土壤，并采用烘干法进行测定，且每次取土后立即通过目测土样颜色和手感土样湿润度的方法在备用处理中选择与土样相似的土壤进行填充，尽量保证每次取土位置保持一定距离以减小采样的扰动影响。

1.5 模拟效果评估

为验证所建模型的精度及实用性，分别选用决定系数()、平均相对误差(MRE)、平均绝对误差(MAE)、均方根误差(RMSE)及平均精度()对模型进行模拟效果评价。其中，越接近于1，MRE、MAE、RMSE越接近于0，计算误差越小，值越大，预测精度越高，且一般认为当>80%时，模型较符合实际情况。模型评价公式为：

(1)

(2)

(3)

(4)

(5)

1.6 数据处理

采用Microsoft Excel 2016进行数据整理及二维拟合计算，Origin 2018 C软件进行三维拟合绘图，Matlab R 2020b软件对各处理蒸发过程进行Mann-Kendall法突变检验，SPSS 24.0软件对拟合结果进行显著性分析。

2 结果与分析

2.1 土水蒸发比变化规律

2.1.1 土水蒸发比随表层土壤含水量变化阶段划分 Mann-Kendall常用于对独立样本或类型变量及顺序变量的非参数检验。本研究中，土水蒸发比与表层土壤含水量为独立样本分布，故采用Mann-Kendall法对其变化趋势及突变情况进行检验(图2)。由统计变量UF及UB变化过程及交点位置可以看出，各处理土水蒸发比全过程呈下降趋势，除S6为整段显著下降外，其余处理在高含水量到突变值附近为显著降低，突变值附近到低含水量则下降趋势不显著。各处理在显著性水平=0.01检验下均存在下降突变，其中，S1～S5突变位置分别为14.07%，13.13%，13.82%，16.16%，15.84%，S6则存在3个下降突变，考虑到20.95%及23.47% 2个突变点处于试验中后期，可能由于试验结果波动较大而不具代表性，此处只选取最明显突变点30.24%。

图2 各处理土水蒸发比随表层土壤含水量Mann-Kendall统计量曲线

2.1.2 土水蒸发比随表层土壤含水量变化规律 土壤蒸发受覆盖度、自身供水条件及天气条件等多因素综合作用，在消除气象条件影响下，抓关键因素，只考虑表层土壤含水量对土壤蒸发的影响效果。本研究在马己安等对裸土及全覆盖处理蒸发阶段划分的基础上，参考Mann-Kendall突变检验结果，选取与各处理突变位置相近的实测点为临界点进一步将不同砂土混合处理蒸发过程进行划分，二者对比关系见图3(a)。

贾鹏飞有时候给范峥峥拨打电话，范峥峥都不接，她无法面对贾鹏飞，只能暂时回避，谎称很忙，然后挂断电话。他起了疑心，开始寻找、打听、跟踪，终于来到这处他卖力移栽金弹子树的地方。

图3 各处理突变位置含水量与阶段划分临界含水量对比及临界含水量与砂土混合比关系

由于试验前期土壤蒸发受控于外界条件变化，土壤水分充足且蒸发强烈，S1土水蒸发比值在较短时间内维持平稳状态，但由于覆砂土的保墒性差异，S2～S6并未观察到这一状态的存在，而是直接进入降速阶段，最大降幅可达86.67%。随着蒸发的持续进行，土壤含水量不断减小，毛细水迁移能力减弱，S1降速阶段较其余处理滞后出现；而进入水汽扩散阶段，土壤毛细管供水作用停止，各处理土水蒸发比变化较为缓慢，最终趋于平稳(图4)。故将裸土蒸发过程分为3个阶段，其余处理为2个阶段。

图4 各处理土水蒸发比与表层土壤含水量分阶段关系

2.2 基于水面蒸发量和表层土壤含水量的土壤蒸发估算

(6)

(7)

(8)

(9)

(10)

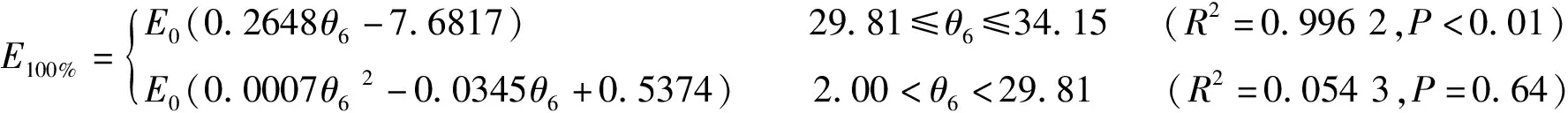
(11)

简化得：

当=0，20%，40%，60%，80%，100%时，

(12)

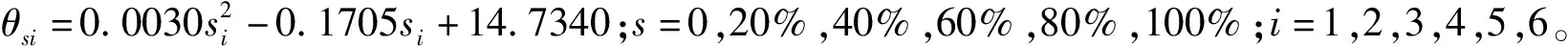
2.2.2 单一模型计算土壤蒸发量与实测土壤蒸发量对比 由图5可知，各处理计算值与实测值基本贴合，且其按分段公式拟合后的决定系数在0.90以上，拟合直线斜率为0.962 3～1.147 1，表明计算土壤蒸发量与实际值相接近。

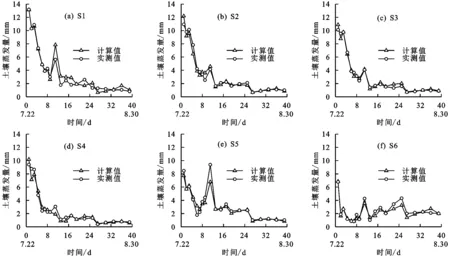
图5 各处理土壤蒸发预测结果与实测值对比及分阶段公式拟合对比关系

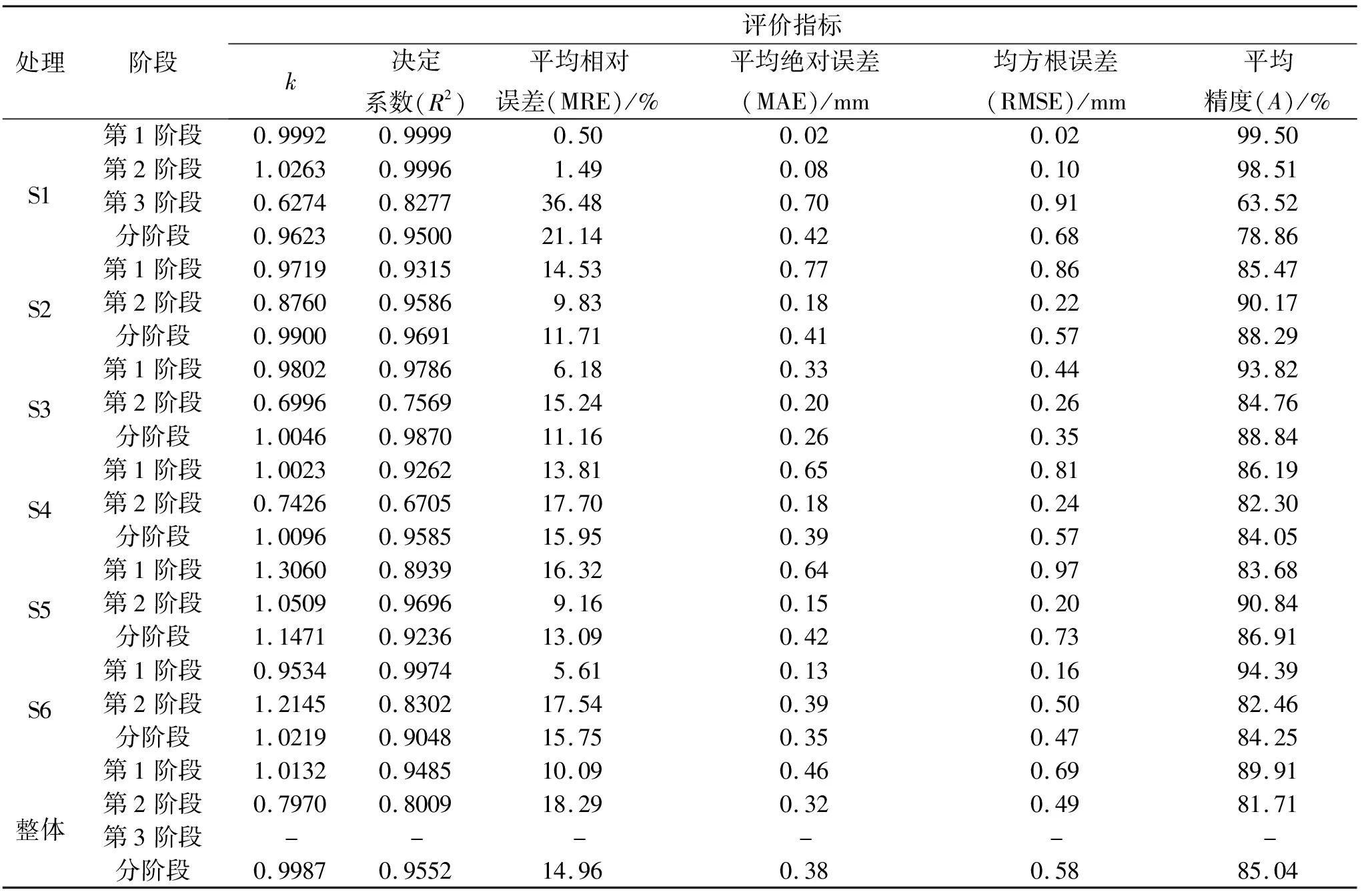
表1 不同处理计算蒸发量与实测蒸发量误差分析结果

其余处理各阶段拟合计算值MAE、RMSE均小于1，且达到80%以上，表明该经验公式对不同砂土混合比处理土壤蒸发量预测具有一定准确性，可进行实际蒸发量估算。

2.3 综合水面蒸发量、表层土壤含水量及砂土混合比的土壤蒸发估算

2.3.1 复合模型构建 由上述建模过程可知，各单一模型与砂土混合比间存在相似关联，为进一步量化单一模型与砂土混合比的函数关系，参考其分阶段过程，分2阶段分别进行二次抛物面及多项式拟合，以寻求综合水面蒸发量、表层土壤含水量与砂土混合比的回归模型。其中，阶段划分所使用的S1～S6临界表层土壤含水量与单一模型相同，即为13.62%，13.69%，13.83%，16.15%，16.25%及29.81%。

由图6可知，第1阶段二次抛物面拟合得公式(13)：

图6 综合水面蒸发量、表层土壤含水量及砂土混合比的分阶段模型

=-07838+14700×10+91010×10-41712×10-53106×10-40423×10

(13)

第2阶段多项式拟合为公式(14)：

=03551-52300×10+56569×10-21045×10+28718×10-12925×10-01178+14330×10-63118×10+10686×10-44571×10

(14)

当≠0，则复合模型为公式(15)：

(15)

2.3.2 复合模型计算土壤蒸发量与实测土壤蒸发量对比 用S1～S6同期实测数据进行验证，2阶段模型及复合模型蒸发量计算值与实测值的MRE、MAE、RMSE及结果分析见图7及表2。最大MRE出现在S6第1阶段及S4第2阶段，对应分别为27.52%，60.81%，可能是因为该处理试验前期数据样本较少，易出现过拟合，而后期观测误差较大，导致欠拟合现象发生，从而降低了预测精度。其余验证处理各指标均处于允许误差范围内，表明该复合模型具有一定适用性，在实际农业生产活动中，当灌水或降雨后，若已知土壤表层含水量及对应水面蒸发量，利用公式(15)便可估算压砂地实际土壤蒸发量，可为宁夏中部干旱带压砂地土壤蒸发量预测提供参考，对于指导农业生产及农田灌溉管理具有现实意义。

表2 阶段模型及复合模型评价指标分析结果

图7 阶段模型及复合模型土壤蒸发量预测值与实测值误差箱线

3 讨 论

土壤蒸发过程一般分为3个阶段，即蒸发稳定阶段、土壤导水率控制阶段及水汽扩散阶段，而土壤含水量是致使土壤处于不同蒸发阶段的根本原因。因此在本研究中，通过统计学方法对各处理土水蒸发比与表层土壤含水量关系寻求下降突变点并进行阶段划分，对于揭示压砂地土壤蒸发过程具有重要意义。本研究指出，覆砂土处理土水蒸发比随表层土壤含水量变化过程均可分为2个阶段，即快速下降阶段与缓慢降低阶段，而不是裸土处理的3个阶段，且砂土混合比越大，主要失水阶段持续时间越短，即阶段临界表层含水量越大。分析认为，砂土覆盖层在土壤表面设置了一道阻滞屏障，能够改善土壤表面及近地层热量及能力交换，延缓水分子由土壤向大气传输的速率，从而不同程度减少蒸发；同时，砂土混合比的增大又改变覆盖层孔隙结构，进一步阻断砂土层与蒸发面的毛管联系，造成土壤蒸发量抑制差异。如吕国安等研究发现，土壤蒸发能力与土壤中土壤与砾石的比例有关；当砂田覆砂层的土砂比从0.09增加到0.57时，土壤含水量由25.30%降低到13.70%，且砂土混合比越大，土壤日蒸发量和累计蒸发量越小，全覆盖时抑蒸效果最好。在本研究中，覆砂土处理蒸发能力低于同期水面蒸发，前期土水蒸发比并未出现稳定蒸发阶段，而表现出持续下降趋势，裸土处理第2阶段与其相比存在滞后性；直至蒸发中后期，表土覆砂处理供水能力与裸土相比较强，蒸发比虽减缓但仍能呈现出较高水平。故在生产实践中，压砂地在多年翻耕后应采取再覆砂等相应措施以维续保墒效果，以避免因砂土比例过小引起失水阶段持续发生，从而造成农田水分的非生产性损耗。

4 结 论

(3)综合水面蒸发量、表层土壤含水量及砂土混合比分2阶段构建了二次抛物面模型及多项式模型，模型整体各评价指标均处于允许误差范围内，具有一定适用性。