基于阶梯形标定物的线激光传感器手眼标定算法

孙炜 舒帅 李汶霖 刘乃铭 苑河南 刘权利

摘要：本文设计了一种阶梯形标定物，这种标定物的标定点坐标更容易获取，只需线激光对准一次标定物上的标记点，与球形标定法相比操作更加简单;同时，在阶梯型标定物的基础上，提出了一种线激光传感器手眼标定算法，该算法利用RASANC（随机抽样一致）算法对标定点进行拟合，并利用最小二乘法求解手眼标定矩阵，这种标定算法无需对标定点的坐标进行修正.实验结果表明，阶梯形标定法的精度和稳定性均优于球形标定法，且该方法操作简单，可以满足自动化加工领域的大部分应用.

关键词：手眼标定;线激光传感器;阶梯形标定物;RASANC算法

中图分类号：TN248

文献标志码：A

随着工业自动化的普及，生产制造领域对工业机器人的需求与日俱增，机器人视觉系统是工业机器人的重要组成部分.在机器人视觉系统中，视觉传感器有两种安装方式：非固定视点方式（eye-in-hand）和固定视点方式（eye-to-hand）.非固定视点方式是将视觉传感器固定在机器人的末端执行器上，机器人运动可带动视觉传感器多视角扫描被测对象;固定视点方式是将视觉传感器与机器人分离，这种安装方式通常会产生视觉死角.本文采用非固定式的安装方法.在机器人的加工生产中，需要通过视觉传感器获取工件的准确位置，以便进行焊接、抓取、涂胶等作业，这时就需要求解视觉传感器坐标系相对于机器人基坐标系的齐次变换关系，上述过程称之为机器人的手眼标定.机器人的手眼标定精度最终会影响整个系统的加工作业精度.

Tsai和Lenz[1]提出了基于视觉传感器的标定板多视角成像方法，并根据约束关系建立AX=XB方程求解手眼关系矩阵，但该方法标定精度较低，鲁棒性弱;Horaud等人[2]提出了一种简化版的手眼标定算法，该算法主要优点在未知数个数不变的前提下，同时解得手眼关系的旋转矩阵和平移向量，但该方法计算复杂度高，易受离群点影响.Liu[3]等人提出了一种精度高、鲁棒性强的手眼标定方法，该方法利用离群点检测解决了数据预处理的问题，显著提高了手眼标定精度，但该方法迭代次数高，计算工作量大;Xie[4]等人提出了一种基于标准球面的手眼标定方法，融合离群点检测和微分计算提高了手眼标定精度，但该方法操作复杂，实验数据庞大;蔡晓洁[5]等人用RASANC算法剔除原始数据中的离群点，取得了更稳定的匹配结果，但其算法计算复杂度高;兰浩[6]等人提出了一种基于球形标定物的线扫描相机手眼标定方法，但该方法操作复杂且极易出错;王英男[7]等人提出了一种适用于线激光器的手眼标定方法，但该方法需要多姿态扫描固定点，计算工作量大;牛延平[8]深入研究了球形标靶拟合及中心定位算法，但该算法的精度易受实验环境和设备的影响;Yang[9]等人提出了一种基于半球面的手眼标定方法，但该方法需要根据视觉传感器设定的坐标系对标定点的y值进行判断，标定容易失败;Hu[10]等人提出了利用单线激光模块辅助摄像机标定的算法，但該算法要求采集到的激光轮廓数据与机器人的姿态数据必须成非线性关系;Zeng[11]等人提出了一种分步式手眼标定算法，该算法首先通过最小二乘法解得旋转矩阵，再由旋转矩阵求得平移向量，但该方法过程繁琐且计算复杂;Liska等人[12]提出了一种二维激光轮廓扫描相机的手眼标定方法，该方法利用迭代算法分步求解手眼关系矩阵，但未剔除离群点且迭代周期长.

1线激光传感器手眼标定

1.1球形标定法原理

目前，在线激光传感器的手眼标定算法中，基于球形标定物的标定算法应用最为广泛.该方法通过线激光传感器扫描球形标定物，以标准球的球心作为标定点，控制机器人带动线激光传感器多位姿扫描标准球，再根据球形标定物的几何特性[6]和勾股定理求取标准球球心在线激光传感器坐标系下的坐标，计算流程如下：

设标准球的球心P在机器人基坐标下的坐标为Pb（xb，yb，zb），在线激光传感器坐标系下的坐标为Ps（xs，ys，zs），Ps可通过式（1）转换到Pb.

式中：bT为机器人工具坐标系相对于机器人基坐标系的齐次变换矩阵，在对机器人进行TCP标定后，bTt可直接从机器人的示教器中读出，是已知量;tT是线s激光传感器坐标系相对于机器人工具坐标系的齐次变换矩阵，当线激光传感器安装在机器人末端执行器上后，tT是固定不变的.手眼标定的本质就是计算s齐次变换矩阵stT.设线激光在标准球上投射形成的激光圆的圆心在线激光传感器坐标系下的坐标为O（x0，y0，z0），标准球球心在线激光传感器坐标系下的坐标为Ps（xs，ys，zs），坐标O与坐标Ps的几何关系如图1所示.

由图1可知，激光圆的圆心坐标与标准球的球心坐标存在式（2）的关系：

式中：R为标准球体的半径，r为激光圆的半径，ys的正负需要根据线激光传感器设定的坐标系方向来判断.线激光传感器多次扫描后可构成点集Psi=（Ps1，Ps2，...，Psn），Pbi=（Pb1，Pb2，...，Pbn），i=1，2，3，...，n，n为线激光传感器扫描的次数.以扫描4次为例，将获得的Pbi和Psi代入式（1）中，再运用最小二乘法求解，便解得手眼标定的齐次变换矩阵stT.

在实际标定过程中，基于球形标定物的手眼标定算法主要存在以下问题：首先，触碰标准球可能会导致标准球的位置发生改变，进而导致标准球的球心在机器人基坐标系下的坐标发生变化;其次，某些末端执行器（例如抓手）无法通过直接触碰标准球表面的方式进行手眼标定，获取标准球的球心坐标变得更加困难;同时，基于球形标定物的手眼标定算法至少需要机器人4次以不同的姿态扫描标准球，且对于每次激光轮廓传感器采集的数据，都需要进行圆分割和拟合，计算复杂度高，标定过程复杂;同时，在获取标准球球心在线激光传感器坐标系下的坐标值过程中，需要根据激光传感器设定的坐标系方向判断y值的正负，该过程容易出错，且出错后将导致标定失败;此外易受到噪声等因素的影响，球形标定法的标定结果鲁棒性较差，上述因素容易造成标定精度不理想，标定结果不稳定.

1.2改进方法

为解决基于球形标定物的线激光传感器标定算法精度低且标定过程繁琐的问题，本文设计了一种阶梯形标定物，并基于阶梯形标定物提出了一种线激光传感器标定算法

1.2.1标定物设计

针对基于球形标定物的线激光传感器标定过程繁琐的问题，本文设计了一种阶梯型标定物，阶梯形标定物的实物图如图2所示.

该阶梯形标定物由正方体合金块切得，其加工精度为a，长、宽、高分别为l、w、h，每层阶梯的高度为b，且每级阶梯上有两个标记点.

阶梯型标定物的三视图如图3所示，图3（a）、图3（b）、图3（c）分别为该标定物的正视图、俯视图、左视图.俯视图中每个阶梯上有两个标记点，標记点将每层阶梯的长度三等分，也可以被称为三等分点.

1.2.2基于阶梯形标定物改进的标定算法

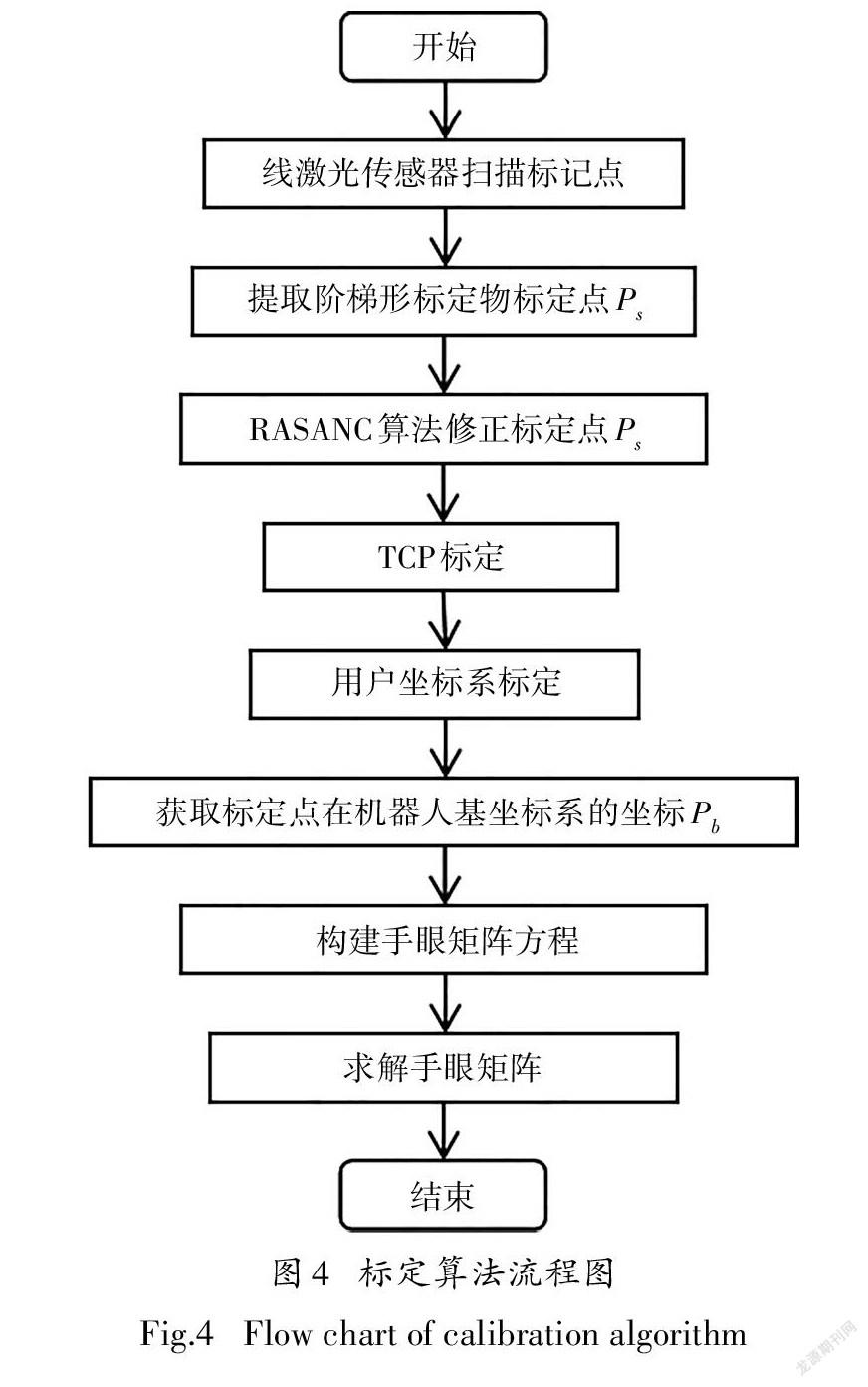
本文提出的标定算法分为如下几步：1）获取标定点在线激光传感器坐标系下的坐标Ps;2）获取标定点在机器人基坐标系下的坐标Pb;3）利用Pb和Ps建立约束方程，通过最小二乘法求解手眼关系矩阵.

本文提出的标定算法流程如图4所示.

1）获取标定点在线激光传感器坐标系下的坐标Ps

本文选取阶梯形标定物的角点作为标定点，这些角点构成实验标定点集;为获得标定点在线激光传感器坐标系下的坐标Ps，需要机器人带动线激光传感器运动，并使线激光对齐阶梯型标定物上同侧的每一个标记点，如图5所示;再利用线激光传感器扫描阶梯形标定物并获取阶梯的轮廓数据，提取阶梯轮廓数据的每个标定点Psi（xsi，0，zsi），i=1，2，3，...，n，n为标定点的总数;本文使用前轮廓的角点作为标定点集Pnew，如图6所示.

由于球形标定法需要对球心坐标的y值进行修正，若未修正，则会导致手眼标定精度较低.为解决这一问题，本文将线激光传感器的扫描平面设置为XOZ平面，则标定点在线激光传感器坐标系下的坐标可表示为（xs，0，zs），通过这种方法可以不需要对标定点的y值进行修正.

获取标定点集Pnew的具体计算方法如下：（a）设阶梯轮廓数据共有k个标定点，设第i个标定点在线激光传感器坐标系下的坐标为（xi，0，zi），i=1，2，3，...，k，k为轮廓数据中标定点的总数;对每一个点（xi，0，zi）做式（3）的运算，求取di，式（3）中sinθ，cosθ计算方式分别如式（4）、式（5）所示：

（b）取di值最大时对应的点，若大于设定的阈值，则判断该点为角点，并保存该点，设该点的索引

为l，则以点（xl，0，zl）为分界，将该轮廓分割为前后两个子集合，继续递归搜索前轮廓的角点直至检测到所有角点，这些角点构成标定点集Pnew;否则，判定该轮廓为直线，不存在角点，结束标定点搜索.

（c）在获得阶梯形标定物轮廓的标定点集后，利用RASANC算法[13]对标定点集Pnew进行直线拟合，拟合得到的直线方程为ax+bz+c=0，并根据直线方程修正离群的标定点.具体方法如下：计算标定点集P中每个点到拟合直线的距离d，若d大于用户设置的阈值Δs，则认为该点为离群点，将该点的x坐标代入拟合直线中，对该点进行修正，用修正后的点替代离群点;否则，不存在离群点，无需对特征点进行修正.

经过上述流程，可以得到标定点在线激光传感器坐标系下的坐标P（x，0，z），i=1，2，3，...，n，n为P中标定点的总数.

2）获取标定点在机器人基坐标系下的坐标P。

为获得工具坐标系相对于机器人基坐标系的齐次变换矩阵T，机器人需要进行TCP标定;本文使用的阶梯形标定物，其加工精度为a=0.1mm，长、宽、高分别为l=9cm、w=9cm、h=9cm，每级阶梯的高度b=1cm;由于阶梯形标定物的尺寸已知且几何特性明显，为更方便地获取标定点在机器人基坐标系下的坐标P，机器人以该阶梯形标定物标定用户坐标系，如图7所示.

由图7可知，本文以点o建立o-xyz用户坐标系，则根据标定的尺寸获取每个标定点在用户坐标系的坐标P=（x，y，z），i=1，2，3，...，n，n为标定点总uiuiuiui数，如点P（0，3，0）.再通过P=bT⋅P可得该特征biuui点在机器人基坐标系下的坐标Pbi=（xbi，ybi，zbi），i=

1，2，3，...，n，n为标定点总数.其中用户坐标系相对于机器人基坐标系的齐次变换矩阵ubT可直接从机器人的示教器中读出，是已知量.

3）求解手眼关系的齐次变换矩阵

设阶梯形标定物上某一标定点P在线激光传感器坐标系下的坐标为Ps（xs，0，zs），在机器人基坐标系下的坐标为Pb（xb，yb，zb），Ps通过式（6）转换为Pb.

式中：T为机器人工具坐标系相对于机器人基坐标系的齐次变换矩阵，机器人进行TCP标定后，T可直接从示教器中读出，是已知量;T是线激光传感器坐标系相对于机器人工具坐标系的齐次变换矩阵，即需要求解的手眼标定矩阵将式（6）中的T展开为式（7）：

式中：R3x3为T的旋转矩阵，t3×1为T的平移向量，共有12个未知量，即T11，T12，T13，T21，T22，T23，T31，T32，33，x，y，2.

将式（6）展开为式（8）：

式中：btR为tbT的旋转矩阵，btt为tbT的平移向量;机器人进行TCP标定后，bT中的数据全部为已知量.由式t（8）知，标定点在线激光传感器坐标系的坐标为（x，0，z，不需要根据线激光传感器设定的坐标系对y坐标值进行修正，该方法巧妙地弥补了球形标定法的不足，提高了实验结果的精度.

式（8）左乘tbT的逆矩阵tbT-1，可得到（9）：

式（9）展开可得式（10）：

将式（10）展开可得式（11）：

根据式（11）可知，该方程组存在9个未知量，即r11，r13，r21，r23，r31，r33，x，y，z，而（Pb，Ps）构成的一组点可以确定三个约束方程，则解出式（11）只需要三组点;将式（11）转化为式（12）：

若特征点集Pnew中存在n个点，则将（Pbi，Psi）构成的n组点代入式（12）可得式（13）：

式（13）中，当n>3时，构成的矩阵方程不再是方阵，不存在解析解，此时利用最小二乘法求解矩阵方程的近似解，将式（13）简写为式（14）：

通过式（15）可解得9个未知量，即r11，r13，r21，r23，r31，r33，x，y，z，剩下的未知量r12，r22，r32可通过向量叉乘计算得到，如式（16）所示：

（r12，r22，r32）=（r11，r21，r31）×（r13，r23，r33）（16）

至此，解得手眼矩阵tsT中全部的未知量，完成手眼标定.

本节设计了一种阶梯形标定物，并提出了一种线激光传感器标定算法，该算法只需扫描一次标定物，提取阶梯轮廓数据中的每个标定点，并利用RASANC算法对标定点进行直线拟合，修正离群点;再通过用户坐标系获取标定点在机器人基坐标系下的坐标，最后利用最小二乘法解出手眼标定矩阵.

与球形标定物相比，本文仅需扫描一次阶梯形标定物就可以快速计算出手眼标定矩阵，且无需对线激光传感器所得的轮廓数据进行区域分割、圆形拟合等操作，计算量大幅度减少;同时，也不需要对标定点的y坐标额外计算，提高了标定结果的精度.

2实验与分析2.1实验条件

本文实验平台的硬件环境和软件环境如表1所示.本文搭建的实验平台如图8所示.利用球形标定法求解手眼标定矩阵后，控制机器人带动线激光传感器多位置、多姿态扫描实验平台上的任意点，同时记录该点在机器人基坐标系下的坐标P，在线real_base激光传感器坐标系下的坐标Ptest_sensor，则Preal_base，P构成实验数据点集;再利用阶梯形标定法求解手眼标定矩阵，重复上述步骤.

线激光传感器固定在机器人末端执行器上，按照上述实验步骤进行标定实验，基于球形标定物的标定实验如图9所示，基于阶梯形标定物的标定实验如图10所示.

2.2精度分析

在解得手眼标定矩阵后，控制机器人带动线激光传感器扫描实验平台上的多个任意点，同时记录每一个点在机器人基坐标系下的实际坐标Preal_base_i在线激光传感器坐标系下的坐标Ptest_sensor_i，i=1，2，3，...，n，n为选取的点总数，（Preal_base_i，Ptest_sensor_i）构成实验数据点集;再结合已求得的手眼标定矩阵，将传感器坐标系下的坐标Ptest_sensor_i代入式（6）计算该点在机器人基坐标系的理论坐标Ptest_base_i，并计算出每一组点的Ptest_base_i与Preal_base_i的差值，利用差值评测球形标定法和阶梯形标定法的实验精度.

表2左侧为伯朗特机器人通过球形标定法解得手眼矩阵后，选取实验平台上任意5点作为实验点的实验结果，并在实验过程中标记选取的5个点;表2右侧为伯朗特机器人通过阶梯形标定法解得手眼标定矩阵后，带动线激光传感器扫描上述5个标记点作为实验点的实验结果.

由表3可知，球形标定法的最大误差几乎是阶梯形标定法的两倍，同时，球形标定法的平均误差稳定在0.25mm左右，而阶梯形标定法的平均误差稳定在0.15mm左右，阶梯形标定法的精度优于球形标定法，且可以满足工业生产要求.

2.3稳定性分析

在解得手眼标定矩阵后，控制机器人带动线激光传感器多位姿扫描实验平台上任一固定点P，获取该点在线激光传感器坐标系下的坐标Ptest_sensor_i，i=1，2，3，...，n，n为扫描总次数，再控制机器人末端执行器触碰该固定点，并记录点P在机器人基坐标系下的实际坐标Preal_base，（Preal_base，Ptest_sensor_i）构成实验数据点集;再结合已求得的手眼标定矩阵，将线激光传感器坐标系下的坐标Ptest_sensor_i代入式（6）计算该点在机器人基坐标系的理论坐标Ptest_base_i，并计算出每一组点Ptest_base_i与Preal_base的差值;为了更直观地评估标定算法的稳定性，本文利用差值的3倍标准差3δ評测球形标定法和阶梯形标定法的稳定性.3δ越小，说明稳定性越强，反之，说明稳定性越差.本节对任一固定点P多位姿扫描5次分析稳定性.

伯朗特手眼标定稳定性分析如表4所示.

表4左侧为伯朗特机器人通过球形标定法解得手眼标定矩阵后，选取点作为实验固定点的实验结果，实验结果表明球形标定法的单坐标轴最大3倍标准差在0.424mm左右;表4右侧为伯朗特机器人通过阶梯形标定法解得手眼标定矩阵后，选取点P作为实验固定点的实验结果，实验结果表明阶梯形标定法的单坐标轴最大3倍标准差在0.15mm左右.阶梯形标定法的稳定性优于球形标定法，足以满足许多复杂的工业现场要求.

2.4算法复杂度分析

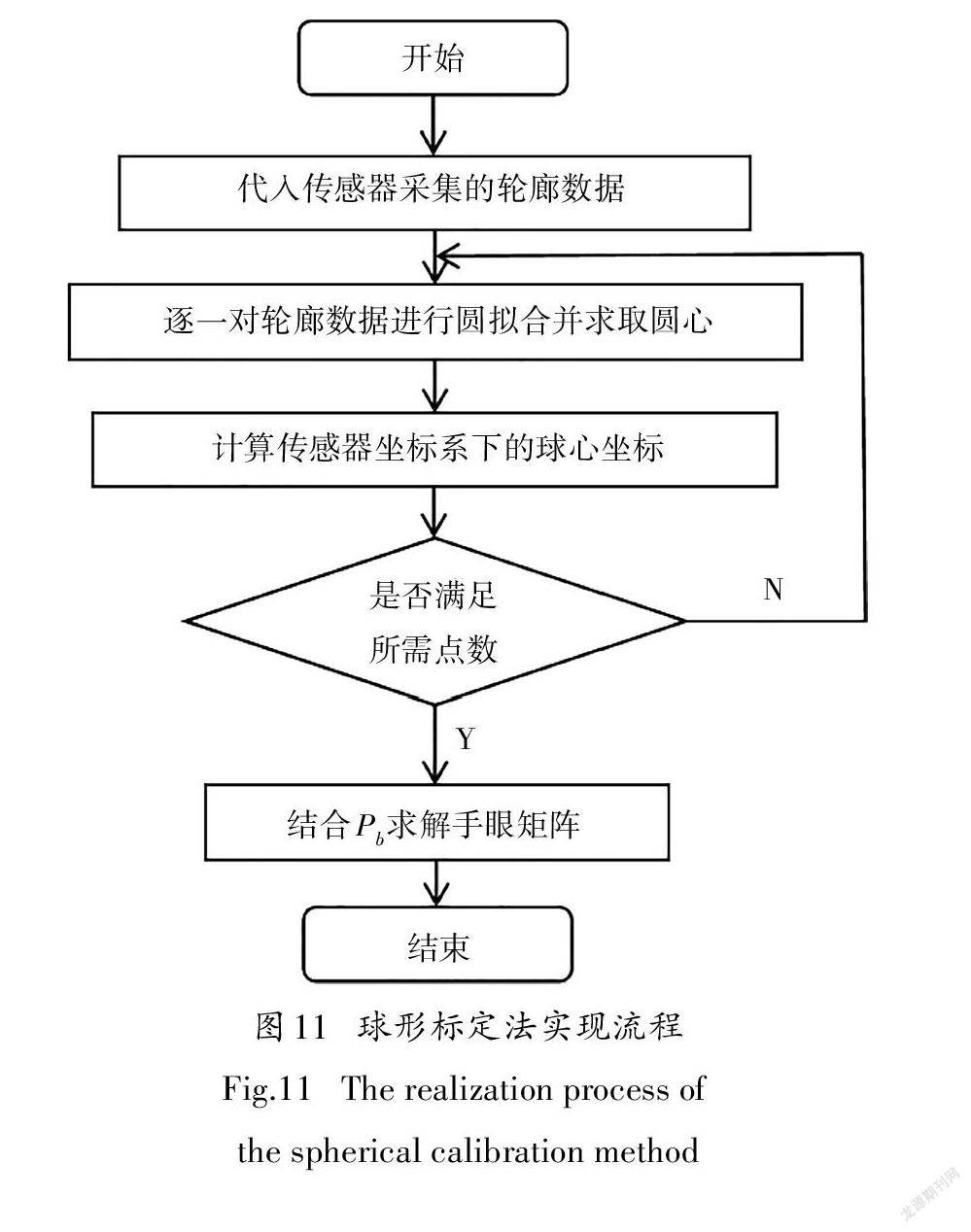
由实验数据可知，本文的算法精度高于传统的球形标定法;此外对比球形标定算法和本文算法的计算用时以表征算法的复杂度，用时少，说明算法复杂度低;反之，算法复杂度高.两种算法的软件实验流程分别如图11和图12所示.

在同等情况下，对两种算法各取5组点进行5次0.25实验，并计算5次实验的平均耗时Tˉ，统计结果如表5所示

由表5可知，传统的球形标定法平均耗时在2.5s左右，而本文提出的算法平均耗时在0.474s左右，该方法显著提高了算法速度，这对提高生产效率具有重大意义.

2.5标定点集Pnew数量分析

从1.2.2节可知，本文提出的标定算法求解手眼矩阵只需要3组点，但精度一般较低;为保证测量精度和可靠性，本文采用数量不同n的组点，分别利用最小二乘法解得手眼矩阵;在解得手眼矩阵后，再进行精度分析和稳定性分析，寻找最优的组点数量，如图13所示.

由图13和图14可知，组点数量n=4或5时，其精度大小和稳定性基本为一恒值;当n>5时，实验结果的精度和稳定性基本不变，但这样会增加实操的复杂性;若无特殊需求，n=4或5即可满足实际工程需要，且性能较好.

3结论

针对基于球形标定物的手眼标定算法计算复杂度高，标定点坐标难以获取且极易出错的问题，本文设计了一种阶梯形标定物，并基于阶梯形标定物提出了一种手眼标定算法，该算法只需要线激光传感器扫描一次标定物即可获取标定点在线激光传感器坐标系下的坐标，并使用RANSAC算法拟合标定点，再根据这些标定点在机器人基坐标系下的坐标构建手眼方程.阶梯形标定方法求解过程简单，便于实际应用.实验结果表明，阶梯形标定物的精度和稳定性均优于球形标定法，阶梯形标定法的标定精度在0.1mm左右，可以满足工业上的大部分应用.

参考文献

[1] TSAI R Y，LENZ R K.A new technique for fully autonomous and efficient 3D robotics hand/eye calibration[J]. IEEE Transactions on Robotics and Automation，1989，5（3）：345-358.

[2]HORAUD R，DORNAIKA F.Hand-eye calibration[J].The In⁃ternational Journal of Robotics Research，1995，14（3）：195-210.

[3]LIU J，WU J，LI A X. Robust and accurate hand-eye calibration method based on schur matric decomposition. Sensors（Basel）. 2019 Oct 16;19（20）：4490. doi： 10.3390/s19204490. PMID： 31623249;PMCID： PMC6832585.

[4]XIE H，PANG C T，LI W L，et al.Hand-eye calibration and its accuracy analysis in robotic grinding[C]//2015 IEEE International Conference on Automation Science and Engineering（CASE）. August 24-28，2015，Gothenburg，Sweden：IEEE，2015：862-867.

[5]蔡晓洁，娄小平，李伟仙.局部二维特征点马氏距离匹配方法[J].工具技术，2017，51（6）：117-121.

[6]兰浩，张曦，尚继辉.一种基于线扫描相机的手眼标定技术[J].计量与测试技术，2019，46（5）：7-10.

[7]王英男，戴曙光.线激光器的手眼标定方法[J].电子科技，2015，28（7）：183-185.

[8]牛延平.三维激光扫描球形标靶拟合及中心定位[J].电子世界，2020（1）：9-12.

[9] YANG L X，CAO Q X，LIN M J，et al.Robotic hand-eye calibra⁃tion with depth camera：a sphere model approach[C]//2018 4th In⁃ternational Conference on Control，Automation and Robotics （ICCAR）.April 20-23，2018，Auckland，New Zealand：IEEE， 2 0 1 8 ：1 0 4 - 1 1 0 .

[10] HU J S，CHANG Y J.Automatic calibration of hand–eye–work⁃space and camera using hand-mounted line laser[J]. IEEE/ ASME Transactions on Mechatronics，2013，18（6）：1778-1786.

[11] ZENG J，CAO G Z，LI W B，et al.An algorithm of hand-eye cali⁃bration for arc welding robot[C]//2019 16th International Confer⁃ence on Ubiquitous Robots（UR）.June 24-27，2019，Jeju，Korea （ S o u t h ）：I E E E ，2 0 1 9 ：1 - 6 .

[12] LISKA J，VANICEK O，CHALUS M. Hand-eye calibration of a laser profile scanner in robotic welding[C]//2018 IEEE/ASME In⁃ternational Conference on Advanced Intelligent Mechatronics （AIM）.July 9-12，2018，Auckland，New Zealand：IEEE，2018： 316-321.

[13]吳晗，李巍，董明利.基于RANSAC的便携式激光扫描测量臂手眼标定方法[J].计算机工程与应用，2017，53（23）：256-260.