基于ANSYS 和MATLAB 的胶结砂砾石坝断面优化

陈 汭，杨海霞，贾金生，郑璀莹

（1.河海大学 力学与材料学院，江苏 南京 211100； 2.中国水利水电科学研究院，北京 100038）

胶结砂砾石坝是区别混凝土坝和土石坝的新坝型［1］，有就地取材方便、安全经济、漫顶不溃的优点，同时能较好地适应软弱地基。 砂卵石土在我国西南、西北地区有较广分布［2］，探究砂卵石覆盖层上胶结砂砾石坝的应力变形特性、地基承载状况，对该坝型的推广有着积极作用［3］。 国内关于胶结砂砾石坝的研究主要集中于材料特性和坝体稳定性研究层面［4－7］。 贾金生等［6］进行了胶结砂砾石坝断面形式和材料配比对胶结砂砾石料力学性能影响的研究，杨世锋等［8］利用有限元软件对胶结砂砾石坝进行了稳定分析研究。但考虑覆盖层上的胶结砂砾石坝应力变形特征的研究较少，关于胶结砂砾石坝优化设计的研究也较少。

笔者以一座设计阶段的胶结砂砾石坝为例，其坝址处地基覆盖层为砂卵石土层，坝体为胶结砂砾石料，在该工程设计初期采用材料力学法，进行了结构稳定性校核，发现坝基应力超过地基承载力。 由于胶结砂砾石料本构关系呈非线性，材料力学法计算结果不够准确，因此需选择邓肯－张模型（经典模型与修正模型）作为材料本构模型，以了解结构真实的应力分布规律［8］。 笔者首先运用ANSYS 参数化设计命令流（APDL）定义非线性本构模型，基于荷载分步施加进行有限元计算，获得并分析应力变形规律，然后依据材料力学法与有限元分析所得结果，选取优化设计目标，通过ANSYS 与MATLAB 的数据交互，优化坝体断面尺寸，达到应力状态的改良。

1 有限元模型与材料本构关系

1.1 二维有限元模型的建立

运用APDL 建模，顺河向为X轴，垂直河向为Y轴，垂直方向为Z轴。 模型基于设计需求简化后，分为坝体、防渗墙、覆盖层土层、基岩四部分，其中坝体划分为两阶，具体尺寸如图1 所示。 模型在Z方向的厚度取单位厚度1 m，可视为假三维的二维模型。 模型下界面添加全约束，坝基在X方向的两个界面添加X方向约束，模型在Z方向的两个剖面添加Z方向约束。 模型采用映射网格划分，共划分4 910 个网格单元，如图2 所示。

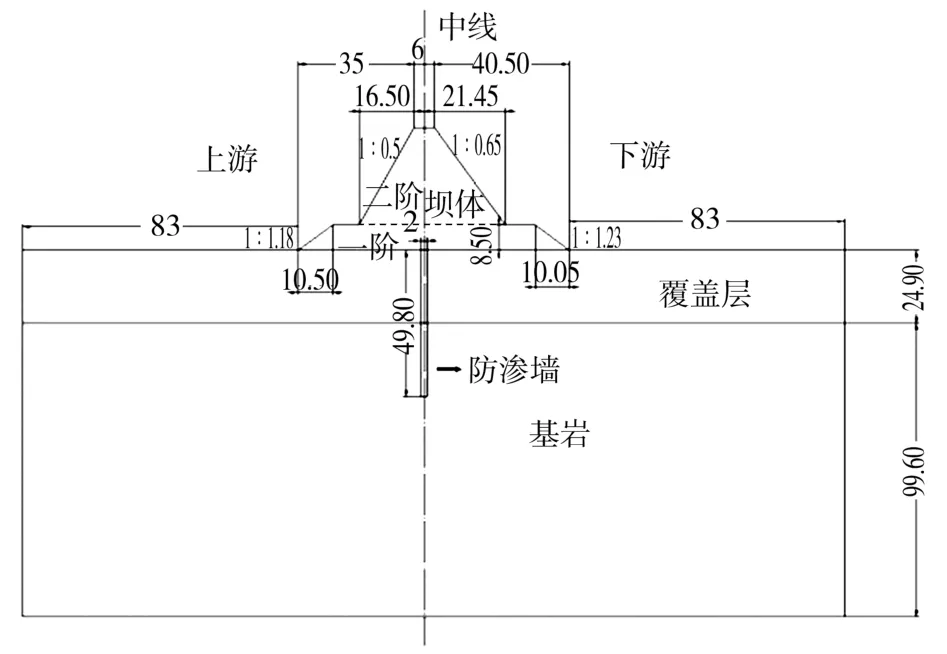
图1 坝体横断面与分区（单位：m）

图2 网格单元划分

1.2 邓肯－张本构模型

根据广义胡克定律建立弹性常数矩阵D，其包含的弹性模量E和泊松比μ都不是常量，而是随应力状态改变的量［9］。 覆盖层为砂卵石土层，采用邓肯－张经典模型［2］。 该工程坝体材料为胶结砂砾石料，应力应变曲线具有双曲线特征，但与传统土石坝不同，需采用经虚加刚性弹簧法修正的邓肯－张模型（后文简称邓肯－张修正模型），该模型解决了应力应变曲线的软化问题，且与其他胶结砂砾石材料本构模型相比，在有限元计算中具有优势［10－14］。

1.2.1 邓肯－张经典模型

判断单元状态：（σ1－ σ3）＜（σ1－ σ3）0且S ＜S0时，单元处于卸载状态，此时弹性模量用Eur表示；反之，单元处于加载状态，此时弹性模量用Et表示。 其中：σ1和σ3分别为单元的大主应力、小主应力；（σ1－σ3）0为历史上单元达到的最大偏应力状态；S为单元的应力水平；S0为历史上单元达到的最大应力水平。

对于加载状态，切线弹性模量Et表达式为

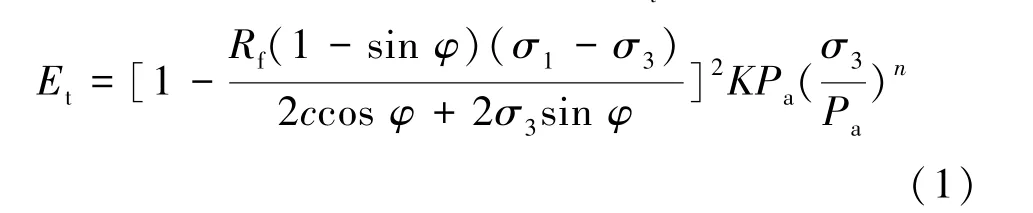
式中：c为材料凝聚力；φ为材料内摩擦角；Pa为标准大气压力；Rf为破坏比；K为弹性模量基数；n为弹性模量指数。

对于卸载状态，切线弹性模量Eur表达式为

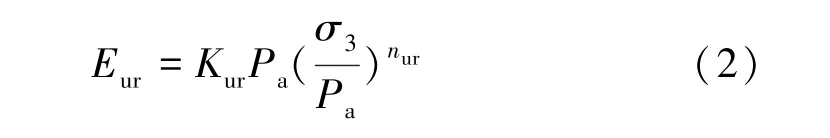
式中：Kur为卸载和再加载时的弹性模量基数；nur为卸载和再加载时的弹性模量指数。

模型的泊松比μ表达式为

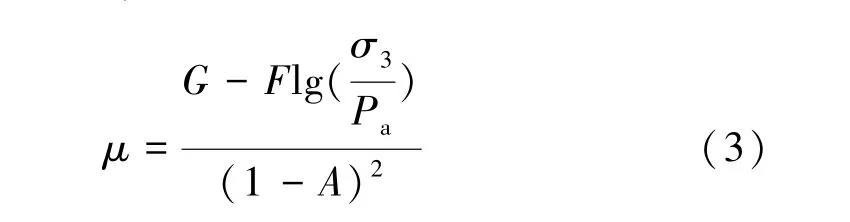
其中

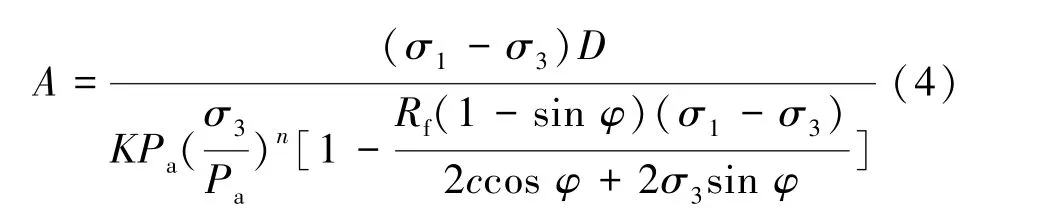
式中：G为切线泊松比基数；F为反映初始切线泊松比随小主应力减小的参数；D为侧向应变与轴向应变关系曲线上小渐进值的倒数。

1.2.2 基于虚加刚性弹簧法的邓肯－张修正模型

图3（a）中①为实际应力应变曲线，②为弹簧应力应变线性关系，在适当位置加虚拟弹簧（如图3（b）所示），①和②叠加即得曲线③，为双曲线，没有应力软化阶段，可用邓肯－张模型表示。 则胶结砂砾石真实切线弹性模量为

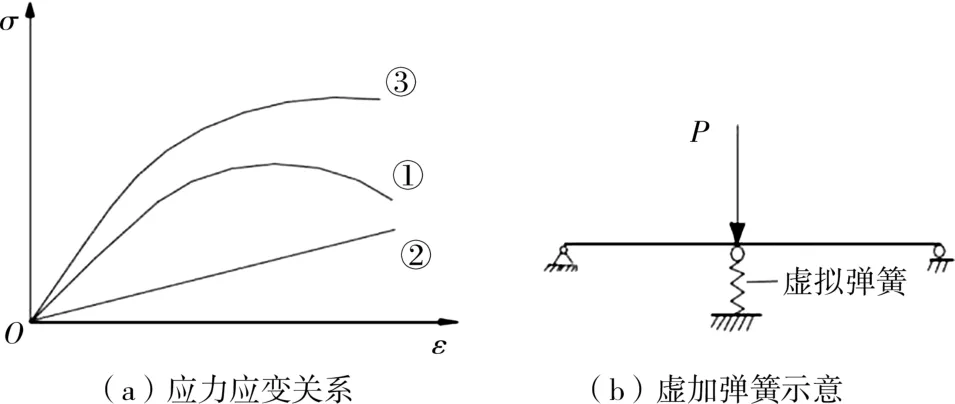
图3 3 种应力应变曲线和虚加弹簧示意

式中：E1为实际胶结砂砾石的切线弹性模量；E2为虚加刚性弹簧的弹性模量，取实际应力应变曲线最大负弹性模量的绝对值；E3为虚拟双曲线的切线弹性模量［11］。

模型参数经过虚加刚性弹簧法处理后便可适用于胶结砂砾石料。 修正模型与经典模型在表达式上一致，但不区分加载、卸载的参数差别，即切线弹性模量Et表达式为式（1）、泊松比μ表达式为式（3）、A的表达式为式（4）。

可以通过三轴固结排水试验得到2 种材料本构模型参数（见表1）。

表1 本构模型参数

1.3 ANSYS 二次开发

1.3.1 建立邓肯－张宏命令

创建本构关系的宏命令文件后，可使各单元在每个荷载步后自动根据应力状态更新弹性常数，简化计算流程［15］。

1.3.2 荷载逐级加载的模拟实现［9，16－17］

逐级加载与瞬间加载效果不同，非线性计算更需分步加载。 计算荷载施加分为9 步，模拟坝体填筑和蓄水过程，填筑过程考虑重力荷载，蓄水过程还考虑静水压力与扬压力，通过ANSYS 的生死单元命令实现该功能。 计算流程如图4 所示。

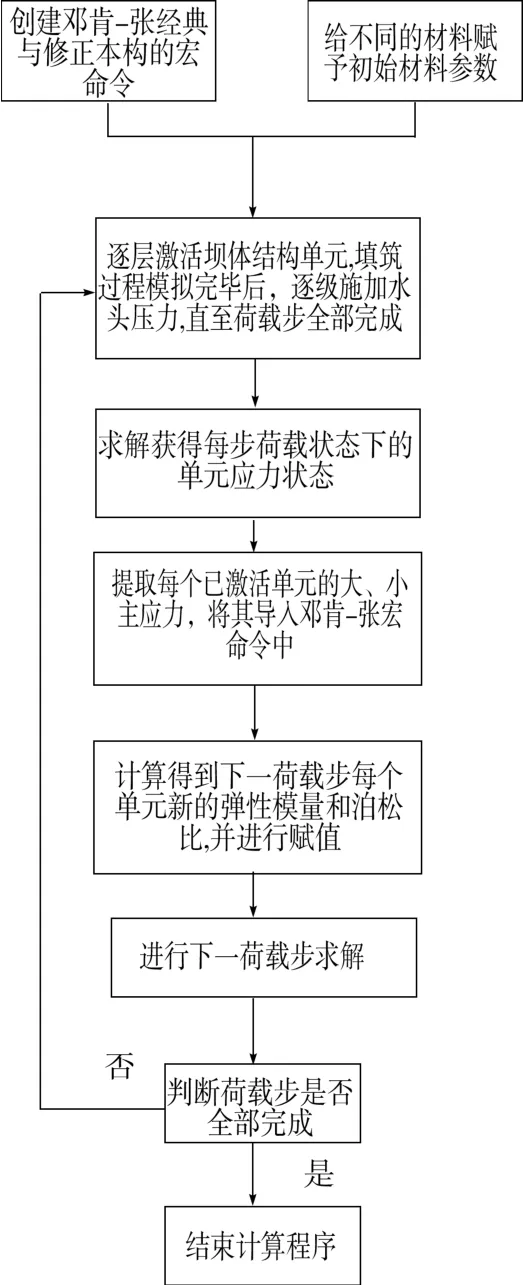
图4 ANSYS 计算流程

1.3.3 重启动技术

ANSYS 非线性计算在荷载步求解完毕后，都需将文件存储目录里的“rst”“rxxx”“ldhi”这3 个文件删除，通过单点重启动保证后续计算正常运行［18］。

1.3.4 约束荷载平衡法

在荷载步计算前读入初始应力文件，产生与原荷载大小相同而方向相反的附加位移，使结构初始位移为零，消除基岩区因自重沉降而产生的影响［19－20］。

2 应力与变形分析

2.1 材料力学法应力校核

在工程设计初期，通过材料力学法进行了坝体稳定性校核，结果见表2，可知坝体抗滑稳定是安全的，但坝踵处应力超过了砂卵石地基的允许承载力，所以设计单位希望通过有限元分析进行复核。 一方面可以通过有限元分析实现非线性本构的定义，计算所得应力结果更符合结构真实应力状态，结构各特征值极值也可为安全性判断提供参考；另一方面可依据材料力学法与有限元分析结果，选取优化设计目标，通过调整断面尺寸，改善结构应力状态。

表2 材料力学法校核结果

2.2 有限元分析结果

由于单元材料间的弹性常数存在差异，因此ANSYS 呈现结果云图时，非线性材料区呈网格状，线弹性材料区则呈片状。 防渗墙会对扬压力和单元弹性常数的连续性产生影响，有限元建模时对防渗墙的存在进行了保留，结果分析仍只讨论坝体和覆盖层结构。

选取竣工期与蓄水期结果进行对比，关键特征值的极值见表3。 对于X向位移，结构极值都不超过1 cm，本文不再分析该特征值。 对于Y方向沉降，坝体极值因扬压力作用更显著而变小，覆盖层极值因静水压力的传递效果而变大，但数值都不超过6.5 cm，不影响结构安全。 对于最大拉应力，坝体挤压覆盖层，在接触面处产生了极值，该数值不影响结构安全。 对于最大压应力，坝体极值为竣工期的2.78 MPa，小于坝体材料的抗压强度（6 MPa），位置变化原因是上游水压力改变了坝体一、二阶结构接触点的挤压效果，使上游接触点挤压减小而下游接触点挤压增大；覆盖层极值为蓄水期时的1.09 MPa，极限点位置与材料力学法结果一致，都为坝踵处。 考虑到剪切破坏是土体主要破坏形式，提取蓄水期覆盖层各节点抗剪强度与最大剪应力差值相对于抗剪强度的比值（称为抗剪强度相对值），该值最大为－0.038，可知覆盖层存在剪切破坏点。

表3 特征值极值及位置

静水压力和扬压力对结构特征值极值影响不大：一是坝体本身断面较厚，且与地基接触面宽，坝型稳定；二是蓄水深度不大，且因防渗墙的存在而对扬压力进行了折减，两种荷载作用有限。

3 优化设计

3.1 优化设计要素

优化设计涉及目标函数、设计变量、约束条件3 个要素，需通过数学建模，将优化问题转换为求函数极值问题。

3.1.1 目标函数

由材料力学法结果可知，优化目标应包含地基压应力。 根据有限元分析结果可知，结构变形、结构受拉、坝体受压都在安全范围内，但覆盖层存在剪切破坏点，且其受压极值在有限元法中并无具体控制值。 考虑蓄水期静水压力会加大地基受力，本优化设计目标定为蓄水期覆盖层最大压应力绝对值、覆盖层抗剪强度相对值，通过提取各节点的目标数值进行大小排序，对最劣点进行优化，实现地基应力状态的改良。

3.1.2 设计变量

设计变量为坝体一、二阶的上下游坡比，即X＝［X1，X2，X3，X4］T，其中X1和X2为坝体二阶结构的下游和上游坡比，X3和X4为坝体一阶结构的下游和上游坡比。

3.1.3 约束条件

优化设计的约束条件参考《胶结颗粒料筑坝导则》《混凝土重力坝设计规范》《水闸设计规范》［21－23］，结合材料本构特性与设计需求，设定如下。

（1）几何约束条件。 ①坝体一阶的上下游坡比范围取1 ∶1.5～1 ∶0.6，坝体二阶的上下游坡比范围分别取1 ∶0.4～1 ∶0.7 和1 ∶0.5 ～1 ∶0.8；②优化坝型断面面积S优化不大于初始坝型断面面积S初始。

（2）应力约束条件。 ①坝踵垂直应力不出现拉应力；②坝体上游面不出现拉应力；③坝体最大主压应力不大于混凝土的最大允许压应力；④坝踵与坝趾的应力比值不大于允许值，该允许值取1.5。

（3）稳定约束条件。 各种荷载组合下坝基面的最小抗滑安全系数Ks不小于允许值［Ks］， ［Ks］取1.05。

3.2 MATLAB 优化计算与ANSYS 有限元分析的交互

APDL 本身具备优化功能，但在进程控制和逻辑框架编制上，操作难度较大［24］，且优化算法只有零阶和一阶两种，在优化算法种类、问题解决适用性上，不如具备丰富优化工具箱的MATLAB。 因此，本优化设计运用了MATLAB 和ANSYS 的混编，即优化主模块在MATLAB 中进行，将ANSYS 有限元分析视为计算子程序进行调用。 软件混编的实现，结合了MATLAB强大的优化功能和ANSYS 良好的有限元分析性能，提供了一种有限元优化设计的借鉴思路。 数据交互流程如图5 所示。 MATLAB 优化计算使用MATLAB 优化工具箱中全局优化工具Patten Searsh。

图5 MATLAB 与ANSYS 数据交互流程

3.3 优化结果分析

表4 列出了初始坝型和优化坝型的特征值，优化坝型一和优化坝型二分别为覆盖层抗压、抗剪优化坝型。 优化坝型一和优化坝型二断面对比见图6、主应力云图对比见图7。

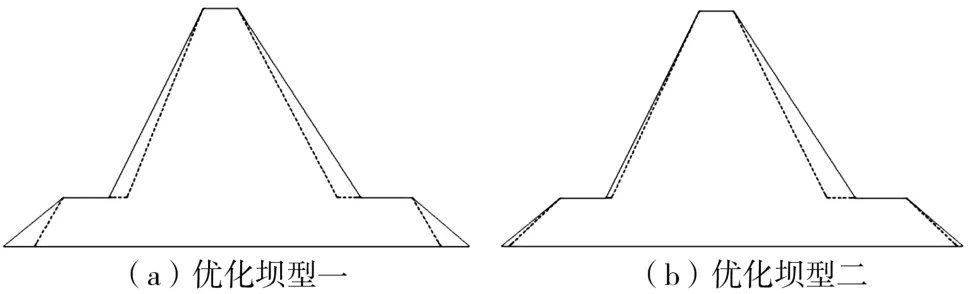
图6 优化坝型一和优化坝型二断面对比

图7 优化坝型一和优化坝型二主应力云图对比（单位：Pa）

表4 各特征值优化效果

3.4 优化方案评估

优化坝型一的4 个坡比都显著增大，优化原理是通过减小坝体体量，降低覆盖层受压效果。 优化坝型二的二阶坡比增大而一阶坡比变化很小，优化原理是通过地基接触面宽度与断面尺寸的平衡，实现了覆盖层抗剪状态的改善。

解决材料力学法结果体现的地基压应力过大问题，是优化设计的目的之一。 在覆盖层压应力优化上，优化坝型一效果更好，且优化坝型一、坝型二的极值点位置都在坝踵处，契合材料力学法所得结果，具有设计指导意义。 剪切破坏虽是土体主要破坏形式，但优化坝型一抗剪状态特征值为正值，可知实现了土体剪切破坏点数量的清零。 在其余特征值的对比上，优化坝型一都比优化坝型二更具优势。 综上，优化坝型一实现了断面面积减少11.3%、覆盖层最大压应力降低9.2%和抗剪破坏点清零，达到了材料用量减少和地基应力状态改良的目的，更符合设计需求。

4 结语

首先，本文从胶结砂砾石料和砂卵石土的材料本构出发，介绍了邓肯－张经典与修正模型通过ANSYS实现的思路，并简要介绍了ANSYS 二次开发的细节，基于此，对初设尺寸的坝型进行了非线性有限元计算，获得了竣工期与蓄水期的特征值，分析其应力变形规律；其次，依据材料力学法和有限元分析结果，以覆盖层抗压、抗剪性能作为优化设计目标，运用数据交互方式，实现ANSYS 与MATLAB 的混编，得到两种优化坝型；最后，将优化坝型与初始坝型的各项特征值进行对比，评判优化效果。

优化目标的设定应符合工程设计需求，设计变量也不只局限于坝型尺寸，可扩展到覆盖层尺寸与结构材料参数。 本文探究了ANSYS 有限元分析与MATLAB优化计算结合的思路，所得优化坝型与特征值可供相关设计单位借鉴，后期会针对不同的设计变量对各目标函数的敏感度做进一步的优化设计。