主动配电网中考虑条件风险价值的智能软开关的规划方法

王 杰，王维庆，王海云，武家辉，王帅飞

主动配电网中考虑条件风险价值的智能软开关的规划方法

王 杰1，王维庆1，王海云1，武家辉1，王帅飞2

(1.可再生能源发电与并网控制教育部工程研究中心(新疆大学)，新疆 乌鲁木齐 830047;2.广东电网惠州供电局，广东 惠州 516001)

针对高比例可再生分布式能源的接入造成主动配电网运行电压越限和支路过载问题，提出了计及网络重构基于条件风险价值理论(conditional value-at-risk, CVaR)的智能软开关(soft open point, SOP)三层规划模型。首先，为了模拟分布电源出力不确定性，建立了基于Wasserstein距离的最优场景。其次，上层模型兼顾了综合成本最小化、安全风险最小化两个目标以确定SOP位置与容量；中层模型以每个场景运行成本最小化为目标进行网络重构；下层运行优化模型中考虑了有载调压变压器、投切电容器组、需求响应以及SOP功率传输多种主动调节措施。为了降低模型求解复杂度，采用基于灰靶决策技术的LDBAS算法和二阶锥优化的混合方法进行求解。最后，以修改的IEEE 33节点配电系统为例，对提出的规划模型进行了验证和分析。

主动配电网；智能软开关；条件风险价值(CVaR)；容量规划；灰靶决策技术；LDBAS算法

0 引言

在可再生分布式电源、智能技术、电力电子技术的融合促进作用下，配电网从被动配电模式逐步过渡到具备多类型分布式电源、积极主动控制与管理、可灵活调节运行拓扑的主动配电模式[1-3]，其目的是提升高比例分布式能源的接纳能力。高比例可再生分布式能源(Distributed Generation, DG)的强易变性和波动性导致配电网运行节点电压越限、支路功率过载，继而实际运行将面临新的经济风险、安全风险问题[4-6]。

应对配电网运行经济、安全问题的传统运行策略主要为网络重构[7-9]。网络重构旨在通过闭/合开关状态优化配电网的拓扑结构，从而改善电能质量、实现负荷均衡，但是传统断路器式联络开关的响应具有时限性以及多频次闭/合会减少设备寿命[7]。因此，基于这些缺陷，配电网中智能软开关解决高比例可再生分布式能源带来的经济、安全问题更具有优势。考虑到智能软开关具有高额的投资与运行费用，SOP合理的安装位置和容量是在实际配电网中得以积极应用的先决条件。

智能软开关是一种替代配电网中联络开关的新型电力电子设备，具有快速、实时、灵活的转供功率能力[10-11]。目前SOP在配电网规划[12-18]、运行优化[19-24]以及运行特性[25-27]层面已经存在相关研究。在配电网规划方面，文献[12]考虑分布式能源的时变特性，建立了SOP规划模型，采用模拟退火和二阶锥规划混合优化方法进行求解。文献[14]建立了以最小化互联配电网电压偏差为目标的SOP规划模型，模型中考虑了SOP不同运行模式，并提出了动态遗传算法编码方式。文献[15]利用有载调压变压器、无功补偿电容器等传统调节手段建立了SOP三层规划模型，采用模拟退火和粒子群的双智能算法进行求解。文献[16]兼顾运行经济性和电压水平建立了SOP和无功补偿装置的规划模型，利用遗传算法和内点法计算模型。文献[17]以分布式电源运营商收益最大化和配电公司综合成本最小化为目标，提出了DG与SOP的协调规划模型，采用遗传算法和锥规划的混合方法求解。然而，以上规划模型并没有考虑配电系统运行面临的不确定性风险。

高比例可再生分布式能源出力很难预测，不确定性因素下的规划模型需要兼顾运行经济性和系统安全风险。文献[28-30]在主动配电网经济运行和安全风险方面已经取得了研究成果，但未能考虑运行与规划的紧密耦合进行多要素协调规划建模，这需要SOP与传统的多种调节措施相结合建立SOP规划模型实现高比例可再生分布式能源的主动适应、积极消纳。

综合上述研究与分析，本文计及网络重构基于条件风险价值(conditional value-at-risk, CVaR)建立了SOP三层规划模型，并针对其规划模型求解复杂的问题，提出了基于灰靶决策技术的天牛须搜索算法(Lévy flight and chaos disturbed beetle antennae search, LDBAS)和二阶锥优化算法的混合方法。首先，为了模拟可再生分布式电源出力的不确定性，基于Wasserstein距离对风电、光伏功率预测值误差建立了最优场景。其次，上层模型属于离散变量的SOP规划问题，采用基于灰靶决策的LDBAS算法求解；中层模型属于网络重构问题，利用LDBAS算法求解；下层模型是一个运行优化问题，采用二阶锥优化算法进行求解。为了进一步降低SOP的投资与运行费用，运行优化模型中考虑了有载调压变压器、投切电容器组、需求响应和SOP功率传输的多种主动调节措施。最后，在修改的IEEE 33节点模型上进行验证与分析。

1 SOP规划问题

1.1 基于Wasserstein距离最优场景

为了考虑可再生分布式能源对SOP安装位置与容量的影响，利用可再生分布式能源预测误差值生成的概率密度函数构建场景，即离散的概率密度分布代替连续的概率密度分布被称为场景生成。预测误差服从零均值的正态分布，采用场景生成法将风电和光伏预测误差的连续概率密度分布离散化，以减小离散场景和原连续概率密度函数之间的误差。本研究采用基于Wasserstein距离构建最优场景，可以实现以较少的场景数更准确地描述连续概率密度分布，避免潮流优化非线性、高维数造成计算困难的问题，假设风电和光伏预测误差的方差分别为预测值的20%和12%[31]。

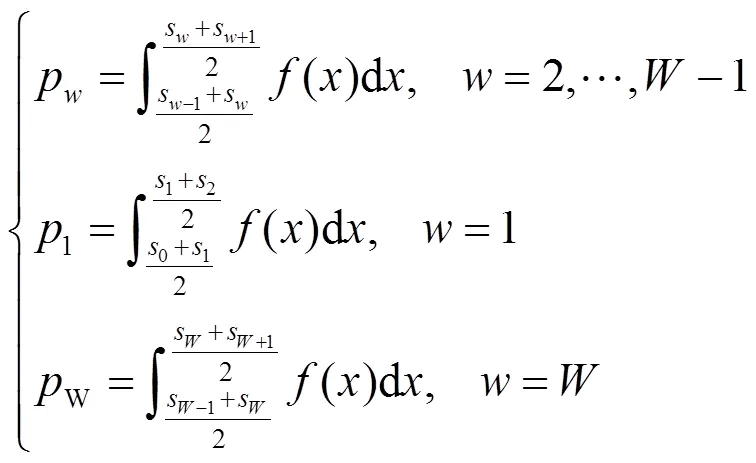
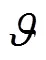
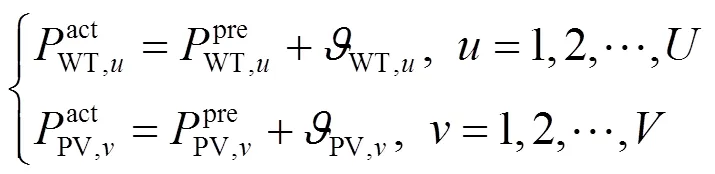
1.2 条件风险价值理论

本研究基于Wasserstein距离构建最优场景数应对高比例可再生分布式能源出力的不确定性造成的配电网经济风险和安全风险。但是个别极端场景会出现经济风险值和安全风险值偏大的情况。针对这一问题，规划模型中引入了条件风险价值理论。

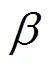
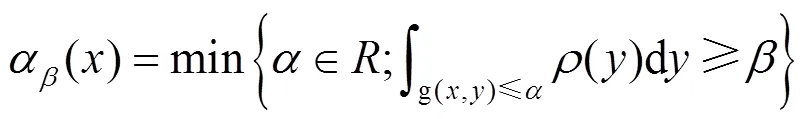
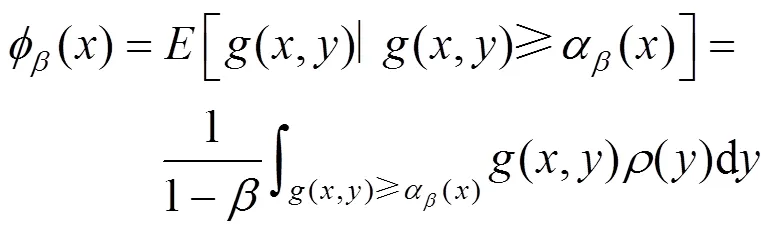
为了便于求解，式(5)可以简化为

1.3 SOP数学模型

一般情况下，SOP是由大功率全控型电力电子元件构成背靠背电压源变流器，并以此拓扑结构研究配电网中SOP规划问题。SOP替代配电网中传统联络开关，连接在两馈线之间，通过快速、实时、灵活地控制有功及无功功率传输，实现负载均衡、改善电能质量、提升高比例分布式能源积极适应能力等目的。本研究所建立规划模型中考虑了SOP损耗系数，并选取SOP的控制模式为PQ-VdcQ模式[14]。图1描述了连接到配电网中馈线I和J终端的SOP接入位置。

图1 SOP 接入位置

(1) SOP有功约束

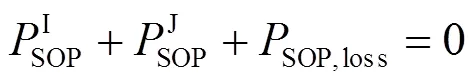
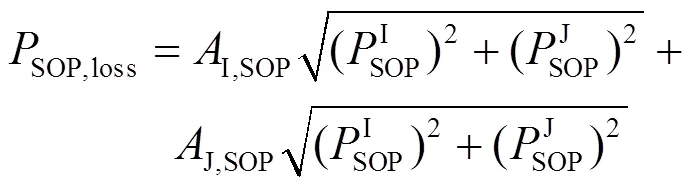
(2) SOP无功约束

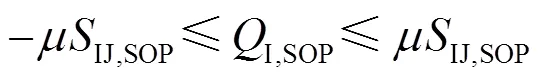
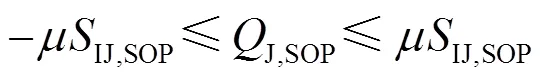
(3) SOP容量约束

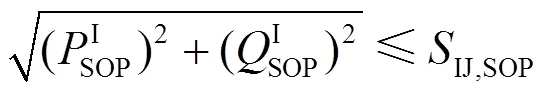
2 基于条件风险价值的SOP规划模型

基于Wasserstein距离构建的最优场景集，本文基于CVaR建立配电规划模型。主动配电网中SOP规划问题不仅需要优化安装位置与容量，而且需要根据确定的位置和容量优化系统运行状态，属于典型的多层规划模型。

1) 上层模型

上层优化模型以最小化年综合成本、最小化安全风险值为优化指标，其数学模型如下：

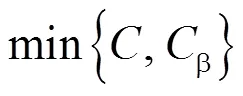
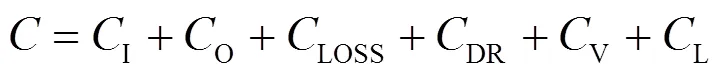
整个配电系统的年度成本由以下三部分组成，具体表达式及物理意义如下。

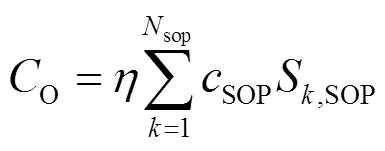
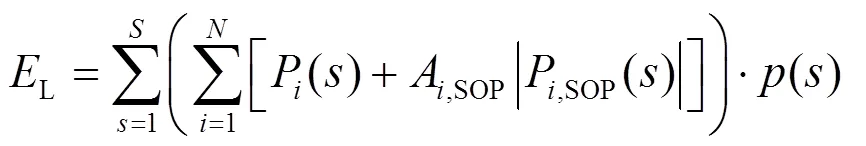
(4) 由于负荷转移会对用户用电带来某种程度的不便利，通过对用户转移电量给予经济补偿的方式定义负荷需求响应的损失值。

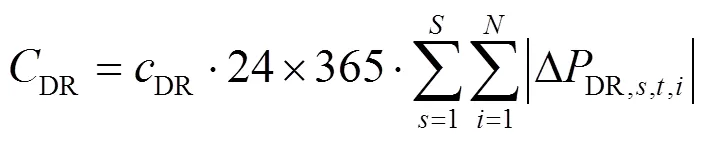
(5) 电压偏差以罚函数的形式添加到目标函数中，使电压偏差尽可能地减小。

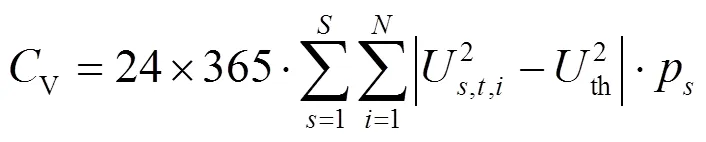
(6) 支路功率过载量同样以罚函数的形式添加到目标函数中，使支路过载量尽可能地减小。

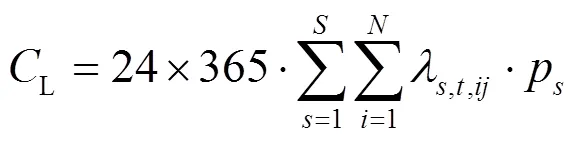
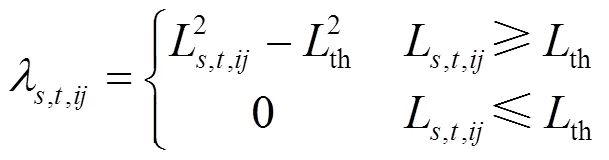
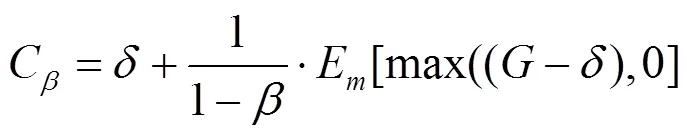
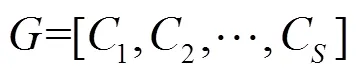
(8) 运行约束条件

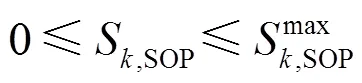
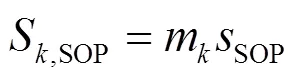
2) 中层模型

中层优化模型属于网络重构问题，下层模型属于系统运行优化问题。在满足配电系统运行约束条件下最小化每个场景网损、SOP运行损耗和需求响应成本之和，目标函数为

在上述SOP约束基础上，需要考虑以下约束：

(1) 潮流约束

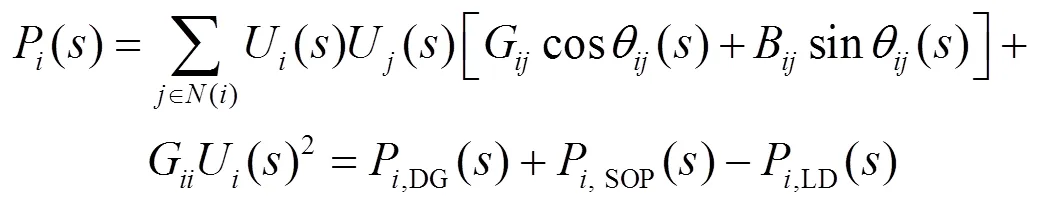
(2) 电压约束

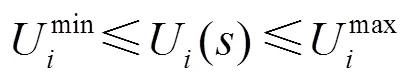
(3) 容量约束

(4) 有载调压变压器运行约束

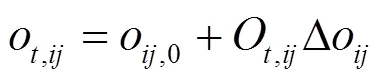
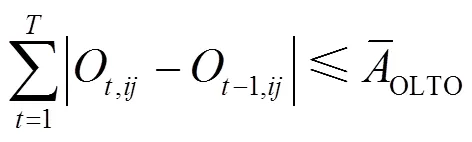
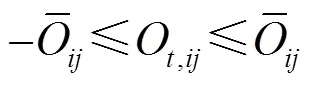
(5) 电容器组投切次数约束

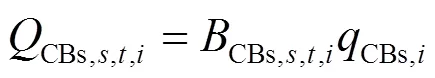
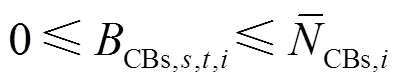
(6) 需求响应约束

为了保证用户正常用电行为，系统内各节点在每个时刻的负荷转移不能超过一定的限值，具体约束表达式如下。

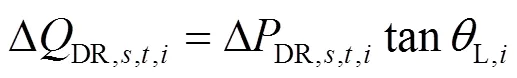
(7) 网络拓扑约束

配电网拓扑结构必须满足辐射状，即无孤立节点、无闭环。

上述模型中决策变量包括：SOP安装位置和容量、电压幅值和相角、开关状态、SOP传输的有功功率和发出的无功功率、节点负荷变化量、有载调压变压器档位和投切电容器组数。

3 SOP三层规划模型求解

3.1 模型求解

针对上述三层模型可以看出，主动配电网中考虑条件风险价值和网络重构的SOP规划模型属于复杂的非线性混合整数规划模型，在确定SOP位置和容量之后，基于SOP在配电网中实时、灵活控制有功功率和无功功率的功能，还考虑了需求响应、网络重构、有载调压变压器、投切电容器组多种调节措施。这使得SOP规划模型具有多层优化的特征，基于多层模型的协调理念，建立了SOP三层协调规划模型。图2给出了模型的主体结构。

由图2主体结构图可以看出，上层模型主要优化主动配电网中的SOP位置与容量问题，目标函数包括综合经济成本和安全风险指标，约束条件包括SOP候选节点的安装容量约束以及SOP容量的离散性约束，采用基于灰靶决策技术的LDBAS算法进行求解。中层和下层模型是在给定SOP位置和容量的基础上每个场景下的运行优化问题，以网络损耗、SOP运行损耗、电压偏差、支路功率偏差以及需求管理成本组成的综合单一优化指标，在满足系统运行的各约束条件基础上实现每个场景下运行最优解：其中，中层模型属于配电网重构问题，在满足网络辐射状结构的条件下寻找每个场景下的最优拓扑结构，采用LDBAS算法求解；下层在满足潮流方程约束、节点电压约束、支路功率约束、有载调压变压器档位改变次数约束、电容器组投切约束以及需求响应约束基础上，基于中层模型确定的拓扑结构实现相应场景下的最优运行方式，属于含SOP配电网离散和连续性混合变量的运行优化问题，采用二阶锥优化方法求解。

图2 三层规划模型框架

SOP三层规划模型相互作用的过程：首先，将上层确定的SOP安装位置及其对应的容量传递给中层和下层模型中，中层和下层模型运行优化后的各项指标返送回上层模型，采用基于灰靶决策技术的LDBAS算法对综合经济成本和安全风险值进行决策。其次，根据给定的SOP位置和容量优化每种场景下网络拓扑结构，下层模型基于各场景下确定的网络拓扑结构运行优化方式，得到每个场景对应的最优各项指标返回到中层模型。

3.2 算法求解流程(图3)

采用LDBAS算法和二阶锥优化相结合的混合方法对上述SOP规划模型进行求解。首先，LDBAS算法用于求解离散变量的上层SOP规划方案和中层重构方案，其中上层是一个多目标优化问题，采用基于灰靶决策的LDBAS多目标进行寻优。其次，利用约束松弛之后的二阶锥规划模型对下层连续和离散混合变量的运行方式进行求解，中层和下层共同作用获取最优运行方式下各项指标。

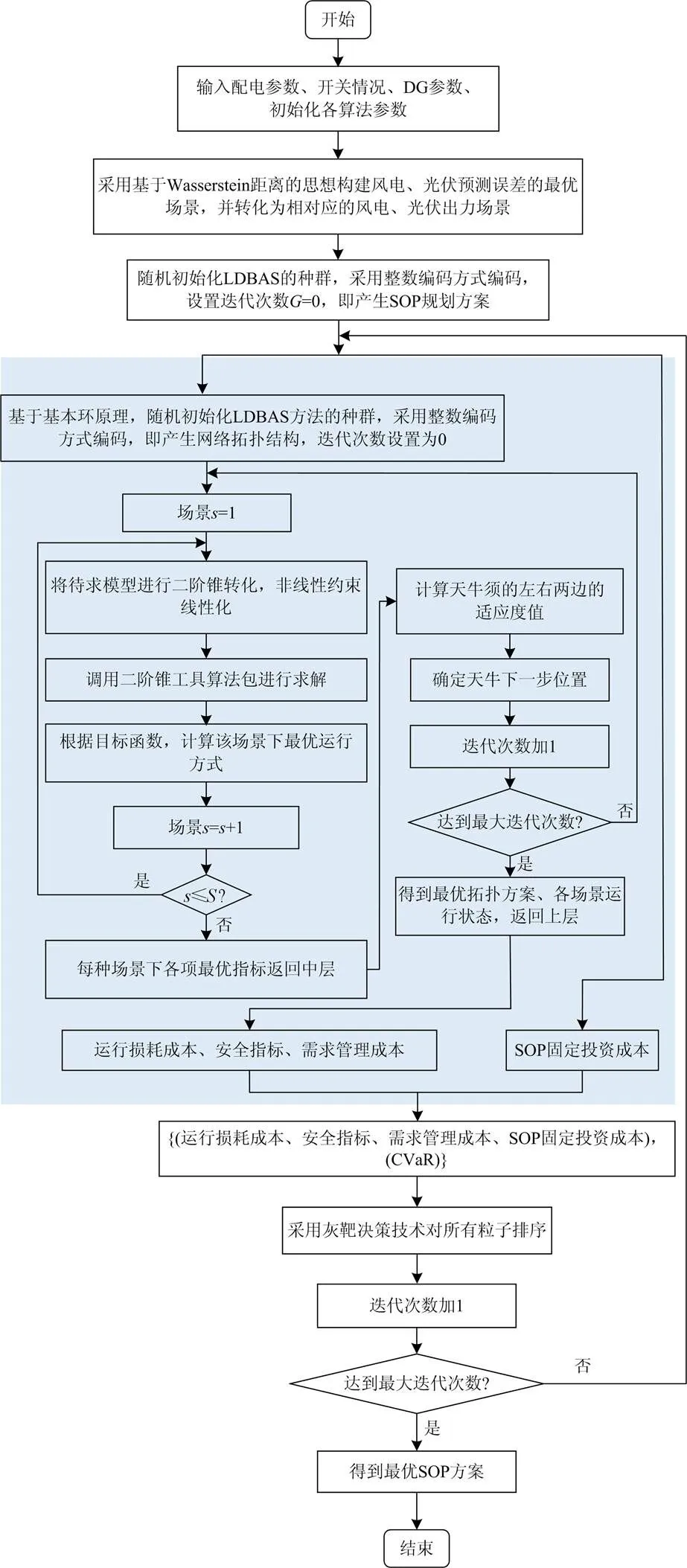
图3 三层协调规划模型求解流程

天牛须搜索算法(Beetle Antennae search algorithm, BAS)是在2017年首次提出的一种基于天牛觅食原理的新智能算法，属于单体搜索算法，具有原理简单、计算速度快的优势。为了避免过早收敛，标准BAS算法中引入了Lévy飞行策略；为了增加局部搜索能力，引入了混沌扰动机制；为了解决模型中多目标问题，引入了灰靶决策技术。基于混沌扰动机制和Lévy飞行策略的天牛须搜索算法(Lévy flight and chaos disturbed beetle antennae search, LDBAS)具有较强的计算效率和准确度。基于灰靶决策技术的LDBAS算法详细理论内容和二阶锥转换方式分别参考文献[33-34]和文献[35]，不再赘述。

主动配电网中考虑条件风险价值和网络重构的SOP规划模型具体求解流程如图3所示。

4 仿真验证与分析

4.1 仿真测试系统

为验证上述提出的三层规划模型的可行性和有效性，在IEEE 33节点配电系统上进行仿真验证。图4给出了IEEE 33节点配电系统简化拓扑结构，电压等级为12.66 kV。SOP的待选方案为模型的联络开关处，IEEE 33节点系统联络开关包括22-12，25-29，33-18，21-8和9-15，并采用基于灰靶决策技术的LDBAS算法和二阶锥优化算法进行计算，分别在Matlab脚本程序和安装的CPLEX工具包进行实现。

图4 IEEE 33节点简化拓扑结构

考虑到可再生分布式能源给含SOP配电系统带来的运行经济性和安全性问题，在标准IEEE 33节点系统上接入了5台风电机组和3组光伏系统，具体配置参数见表1。设定系统接入的所有风电机组和光伏系统环境相同，风电和光伏的典型日出力曲线如图5，表2给出了SOP相关参数。有载调压变压器安装在系统节点1和节点2之间，具有11个调节位置，每个抽头的调节率为1%，档位最大变换次数为4次/天。电容器组接入位置在系统节点33，最大接入组数为5，档位容量为60 kvar。

表1 分布式电源配置参数

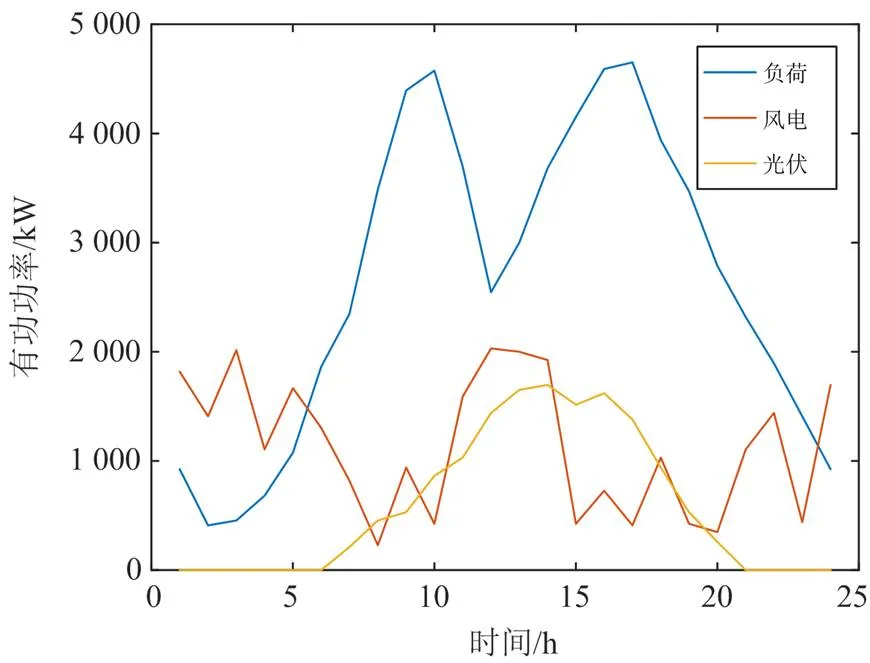
图5 分布式可再生能源和负荷的日运行曲线

表2 SOP参数

4.2 规划结果

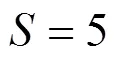
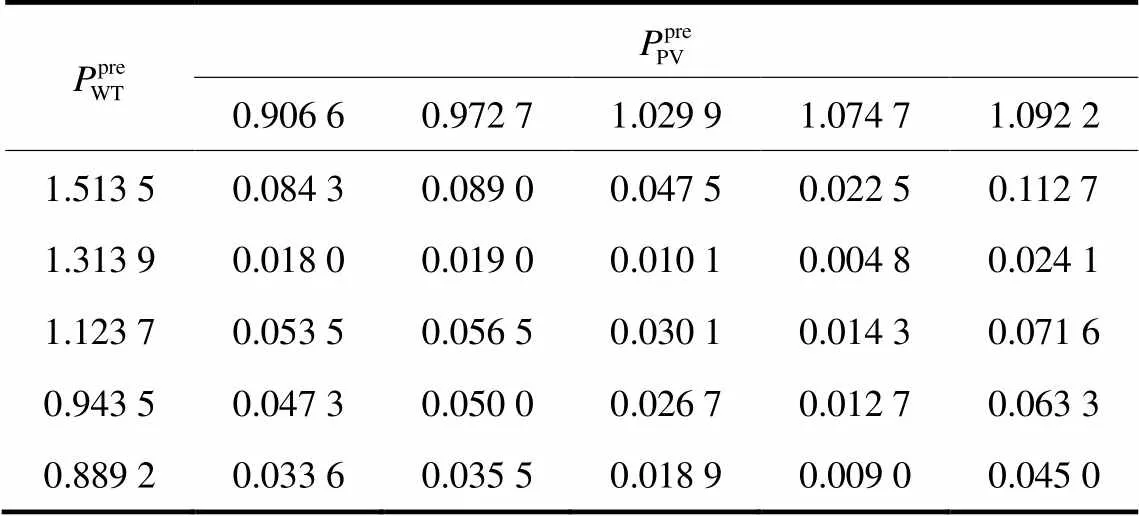
表3 风光场景功率-概率分布

1) CVaR前沿曲线

首先，为了分析不同权重的CVaR值对SOP规划结果的影响，对综合经济指标和安全风险指标通过加权的方式将上层规划模型转化为单一目标的优化问题进行求解，即在CVaR值前赋一个权值系数添加到目标函数中，采用LDBAS算法求解。上层规划模型目标函数表达式转化为

CVaR值加权系数(即偏好系数)可以根据CVaR的偏好来取值，本研究加权系数取为0.35、0.45、0.55、0.65、0.75、0.85、0.95，进而判断在配电系统中SOP规划结果对偏好系数的敏感度，和之和为1。图6给出了不同CVaR偏好系数下SOP规划后综合经济成本和系统安全风险值，安全风险值是安全风险CVaR的值。偏好系数越大表示越偏向考虑系统安全性，由图6结果可以看出，随着偏好系数增大，综合成本越高，而安全风险值越低。因此，在规划SOP时，可以根据自己偏好给CVaR值设定偏好系数，以保证系统运行经济性和安全性的重要程度。然而，根据这种方法给CVaR值设定偏好系数，主观性比较强，从而使得系统损失风险和安全风险与实际偏差较大，造成不必要的经济损失和安全风险。因此，本研究SOP规划模型中，采用基于灰靶决策技术的LDBAS算法来求解，兼顾了系统运行经济性和安全性。

2) SOP规划结果

表4和表5给出了四种SOP规划方案容量配比以及对应的经济成本，结果显示，四种方案损耗成本分别减少了9.971 5万元、12.873 7万元、13.965 8万元和14.360 6万元，四种方案的综合成本分别降低了5.03%、11.85%、19.66%和23.22%。与方案1相比，方案2的运行损耗成本和SOP综合成本分别减少了2.902 2万元和2.901 8万元。因此，可以通过改变变压器档位、投切电容器以及改变负荷用电行为多种调节手段来改善电压质量、缓解系统高负荷运行压力，从而降低SOP投资运行成本；与方案1相比，方案3的SOP规划后系统运行损耗成本和SOP综合成本分别减少了5.18万元和6.93万元，显然，网络重构使得SOP投资运行成本进一步降低。因此，低成本的调节手段可以应对SOP接入配电网的高额投资运行成本。方案3中SOP规划综合成本高于方案4，这是因为在规划过程中方案4未考虑CVaR值。

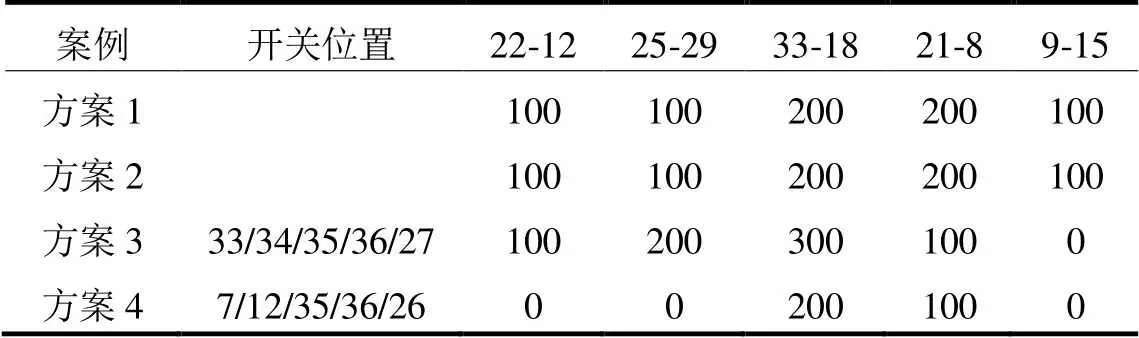
表4 SOP规划位置与容量

表5 不同案例下SOP规划结果

表6给出了各个方案下运行指标成本，很明显，对比四种方案，方案3的安全风险最低。从经济风险角度来看，方案4最具优势，这是因为方案4未考虑CVaR值，以牺牲系统运行的安全性保证了其经济性。进一步，方案3的安全风险指标相对方案4减少了13.70%，而方案4的经济风险成本相对方案3仅降低了1.58%。因此CVaR值参与到SOP的优化配置来评价配电网经济性和安全性具有一定的实用价值。

表6 不同案例下系统运行成本

3) 高比例可再生分布式能源下SOP规划

高比例可再生分布式能源接入到配电网中会影响SOP的规划结果，本研究以分布式能源总接入量与系统总负荷量的比值作为分布式能源的渗透率。

表7和表8给出了DG渗透率为50%、75%、100%、120%和135%下SOP在配电网中规划位置、容量以及投资运行成本结果。从表7中结果可以清晰地看出，系统运行损耗成本随着DG的渗透量增加而增加，从而SOP规划后的综合成本随之增加，但是CVaR值并没有增加，可以说明通过牺牲SOP在系统中部分经济来应对DG高比例渗透率下引起的不安全问题，以促进DG的渗透容量。但是当DG渗透容量达到135%时，综合成本超过了原始系统SOP规划成本，也就是说，权衡安全性和经济成本的损失度，DG渗透容量需要在一定的上限值内。当DG渗透率为75%时，CVaR值最低，同时在主动配电系统中SOP规划比较经济。

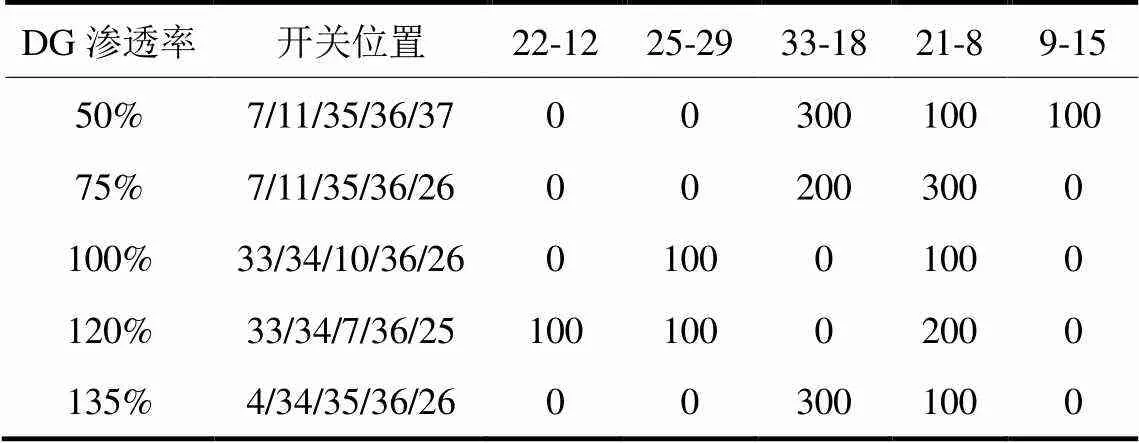
表7 SOP不同DG渗透率下SOP下安装位置和容量

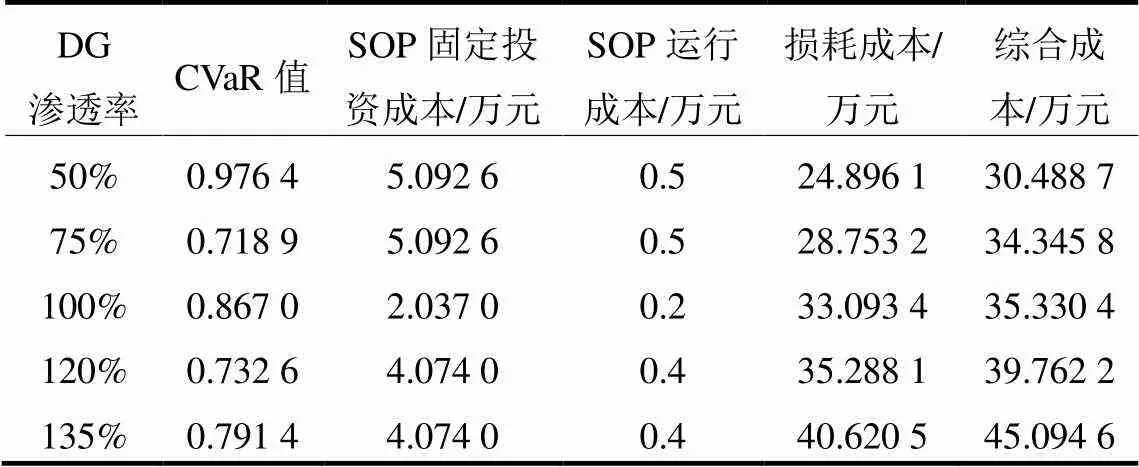
表8 不同DG渗透率下SOP规划结果

4) 算法验证

为了验证基于灰靶决策的LDBAS算法和二阶锥优化混合方法求解SOP规划问题的计算效率，以及基于Wasserstein距离构建最优场景的有效性，将风电和光伏预测误差的概率密度函数等距离离散10个场景。以方案3为例，采用文献[36]中多目标粒子群算法和二阶锥优化的混合方法对提出的SOP三层规划模型进行求解，与本文算法进行对比分析，仿真结果如表9所示。

表9 各算法求解时间对比

从表9可以看出，基于Wasserstein距离构建场景能够有效地得到合理场景数目，提高了SOP三层规划模型的计算效率。与文献[36]中算法对比，本文算法计算时间分别减少了8 908.73 s和9 304.12 s。验证了本文方法的计算效率更高。

5 结论

1) 考虑条件风险价值和网络重构的SOP三层规划模型有效地发挥新型设备在配电网中的作用，降低SOP的投资运行成本，从而提高了配电网的运行经济性且兼顾了系统运行安全性。

2) 本文提出的基于灰靶决策技术的LDBAS算法和二阶锥优化的混合方法提高了计算效率，能够满足大规模混合整数非线性规划问题的求解。

3) 有载调压变压器、投切电容器组、需求响应、网络重构和SOP实时潮流的控制能够有效应对多重随机性叠加的复杂运行场景，规划模型中网络重构通过改变开关状态来满足系统安全与经济运行，以及改善系统潮流分布，从而降低了SOP高额投资运行成本。

4) 研究了不同DG渗透率对SOP在配电网中的规划方案的影响，结果表明：一方面，DG渗透率为75%时，SOP规划后系统经济性和CVaR值最佳；另一方面，牺牲一定程度的SOP投资运行成本能够应对DG出力的不确定性造成的安全风险问题，从而促进DG接入到配电网中的渗透率。

[1] YANG Z, LI Y, XIANG J. Coordination control strategy for power management of active distribution networks[J]. IEEE Transactions on Smart Grid, 2019, 10(5): 5524-5535.

[2] 任佳依, 顾伟, 王勇, 等. 基于模型预测控制的主动配电网多时间尺度有功无功协调调度[J]. 中国电机工程学报, 2018, 38(5): 1397-1407.

REN Jiayi, GU Wei, WANG Yong, et al.Multi-time scale active and reactive power coordinated optimal dispatch in active distribution network based on model predictive control[J].Proceedings of the CSEE, 2018, 38(5): 1397-1407.

[3] 李国梁, 韩军峰, 马平. 基于场景聚类的主动配电网分布式风电的优化配置[J]. 广东电力, 2021, 34(4): 53-58.

LI Guoliang, HAN Junfeng, MA Ping. Optimal allocation of distributed wind power in active distribution network based on scenario clustering[J]. Guangdong Electric Power, 2021, 34(4): 53-58.

[4] VERZIJLBERGH R A, DE L J, LUKSZO Z. Renewable energy sources and responsive demand. Do we need congestion management in the distribution grid?[J]. IEEE Transactions on Power Systems, 2014, 29(5): 2119-2128.

[5] LI R, WONG P, WANG K. et al. Power quality enhancement and engineering application with high permeability distributed photovoltaic access to low-voltage distribution networks in Australia[J]. Protection and Control of Modern Power Systems,2020, 5(3): 183-189.

[6] 李军徽, 冯喜超, 严干贵, 等. 高风电渗透率下的电力系统调频研究综述[J]. 电力系统保护与控制, 2018, 46(2): 163-170.

LI Junhui, FENG Xichao, YAN Gangui, et al. Survey on frequency regulation technology in high wind penetration power system[J]. Power System Protection and Control, 2018, 46(2): 163-170.

[7] 潘本仁, 王和春, 张妍, 等. 含分布式电源的主动配电网重构策略研究[J]. 电力系统保护与控制, 2020, 48(15): 102-107.

PAN Benren, WANG Hechun, ZHANG Yan, et al. Study on an active distribution network reconstruction strategy with distributed power supply[J]. Power System Protection and Control, 2020, 48(15): 102-107.

[8] 倪识远, 张林垚. 考虑动态重构的主动配电网多目标双层优化调度方法[J]. 电力系统保护与控制, 2020, 48(20): 38-47.

NI Shiyuan, ZHANG Linyao. Multi-objective bi-level optimal dispatch method of an active distribution network considering dynamic reconfigurations[J]. Power System Protection and Control, 2020, 48(20): 38-47.

[9] 陈泽兴, 张勇军, 黄豫, 等. 基于条件风险价值的综合能源配电网优化重构方法研究[J]. 全球能源互联网, 2020, 3(6): 590-599.

CHEN Zexing, ZHANG Yongjun, HUANG Yu, et al. Optimal reconfiguration of distribution networks in integrated energy systems based on conditional value at risk[J]. Journal of Global Energy Interconnection, 2020, 3(6): 590-599.

[10]王成山, 宋关羽, 李鹏, 等. 基于智能软开关的智能配电网柔性互联技术及展望[J]. 电力系统自动化, 2016, 40(22): 168-175.

WANG Chengshan, SONG Guanyu, LI Peng, et al.Research and prospect for soft open point based flexible interconnection technology for smart distribution network[J].Automation of Electric Power Systems, 2016, 40(22): 168-175.

[11]孙充勃, 原凯, 李鹏, 等. 基于SOP的多电压等级混联配电网运行二阶锥规划方法[J]. 电网技术, 2019, 43(5): 1599-1605.

SUN Chongbo, YUAN Kai, LI Peng, et al. A second-order cone programming method for hybrid multiple voltage level distribution networks based on soft open points[J].Power System Technology, 2019, 43(5): 1599-1605.

[12] WANG C, SONG G, LI P, et al. Optimal siting and sizing of soft open points in active electrical distribution networks[J]. Applied Energy, 2017, 189: 301-309.

[13] 王俊丰, 孔令生, 范心明, 等. 面向有源配电网运行经济性的智能储能软开关规划[J]. 电力建设, 2020, 41(10): 63-70.

WANG Junfeng, KONG Lingsheng, FAN Xinming, et al. Optimal planning for soft open point integrated with ESS to improve the economy of active distribution network[J]. Electric Power Construction, 2020, 41(10): 63-70.

[14] 叶雨晴, 马啸, 林湘宁, 等. 基于动态GA编码的柔性多状态开关选址策略[J]. 高电压技术, 2020, 46(4): 1171-1181.

YE Yuqing, MA Xiao, LIN Xiangning, et al.Study on site selection of soft open points based on dynamic GA coding strategy[J].High Voltage Engineering, 2020, 46(4): 1171-1181.

[15] 陈垚煜, 耿光超, 江全元, 等. 考虑传统调控手段的配电网SOP选址定容方法[J]. 高电压技术, 2020, 46(4): 1181-1189.

CHEN Yaoyu, GENG Guangchao, JIANG Quanyuan, et al.Optimal siting and sizing method of soft open point in distribution network combined with traditional regulations[J]. High Voltage Engineering, 2020, 46(4): 1181-1189.

[16] 郑焕坤, 石甜静. 基于智能软开关和无功补偿装置的配电网双层优化[J]. 电力系统自动化, 2019, 43(19): 117-123.

ZHENG Huankun, SHI Tianjing.Bi-level optimization of distribution network based on soft open point and reactive power compensation device[J]. Automation of Electric Power Systems, 2019, 43(19): 117-123.

[17] 马丽, 薛飞, 石季英, 等. 有源配电网分布式电源与智能软开关三层协调规划模型[J]. 电力系统自动化, 2018, 42(11): 86-93.

MA Li, XUE Fei, SHI Jiying, et al.Tri-level coordinated planning model of distributed generator and intelligent soft open point for active distribution network[J]. Automation of Electric Power Systems, 2018, 42(11): 86-93.

[18] 何英静, 沈舒仪, 何东, 等. 兼顾网损优化效益与投资成本的SNOP容量规划方法[J]. 中国电力, 2020, 53(4): 32-40.

HE Yingjing, SHEN Shuyi, HE Dong, et al. A SNOP capacity planning method considering network-loss optimization benefit and investment cost[J]. Electric Power, 2020, 53(4): 32-40.

[19] 王成山, 宋关羽, 李鹏, 等. 一种联络开关和智能软开关并存的配电网运行时序优化方法[J]. 中国电机工程学报, 2016, 36(9): 2315-2321.

WANG Chengshan, SONG Guanyu, LI Peng, et al.A hybrid optimization method for distribution network operation with SNOP and tie switch[J].Proceedings of the CSEE, 2016, 36(9): 2315-2321.

[20] QI Q, WU J, LONG C. Multi-objective operation optimization of an electrical distribution network with soft open point[J]. Applied Energy, 2017, 208: 734-744.

[21] DING T, WANG Z, JIA W, et al. Multiperiod distribution system restoration with routing repair crews, mobile electric vehicles, and soft-open-point networked microgrids[J]. IEEE Transactions on Smart Grid, 2020, 11(6): 4795-4808.

[22] LI P. Coordinated control method of voltage and reactive power for active distribution networks based on soft open point[J]. IEEE Transactions on Sustainable Energy, 2017, 8(4): 1430-1442.

[23] 徐全, 袁智勇, 雷金勇, 等. 基于智能软开关的有源配电系统运行灵活性提升方法[J]. 中国电力, 2021, 54(11): 82-90.

XU Quan, YUAN Zhiyong, LEI Jinyong, et al. Improvement of operational flexibility for active distribution networks based on soft open points[J]. Electric Power, 2021, 54(11): 82-90.

[24] 熊正勇, 苗虹, 曾成碧. 基于智能软开关与储能系统联合的有源配电网运行优化[J]. 电测与仪表, 2020, 57(13): 33-39.

XIONG Zhengyong, MIAO Hong, ZENG Chengbi. Operation optimization of active distribution network based on smart soft open point and energy storage system[J]. Electrical Measurement & Instrumentation, 2020, 57(13): 33-39.

[25] 丛鹏伟, 唐巍, 娄铖伟, 等. 含高渗透率可再生能源的主动配电网两阶段柔性软开关与联络开关协调优化控制[J]. 电工技术学报, 2019, 34(6): 1263-1272.

CONG Pengwei, TANG Wei, LOU Chengwei, et al. Two-stage coordination optimization control of soft open point and tie switch in active distribution network with high penetration renewable energy generation[J].Transactions of China Electrotechnical Society, 2019, 34(6): 1263-1272.

[26] LI P, JI H, YU H, et al. Combined decentralized and local voltage control strategy of soft open points in active distribution networks[J]. Applied Energy, 2019, 241: 613-624.

[27] JI H, WANG C, LI P, et al. Robust operation of soft open points in active distribution networks with high penetration of photovoltaic integration[J]. IEEE Transactions on Sustainable Energy, 2019, 10(1): 280-289.

[28] 马瑞, 金艳, 刘鸣春. 基于机会约束规划的主动配电网分布式风光双层优化配置[J]. 电工技术学报, 2016, 31(3): 145-154.

MA Rui, JIN Yan, LIU Mingchun. Bi-level optimal configuration of distributed wind and photovoltaic generations in active distribution network based on chance constrained programming[J]. Transactions of China Electrotechnical Society, 2016, 31(3): 145-154.

[29] 王成山, 孙充勃, 李鹏, 等. 基于SNOP的配电网运行优化及分析[J]. 电力系统自动化, 2015, 39(9): 82-87.

WANG Chengshan, SUN Chongbo, LI Peng, et al. SNOP-based operation optimization and analysis of distribution networks[J]. Automation of Electric Power Systems, 2015, 39(9): 82-87.

[30] 凌万水, 刘刚. 基于鲁棒优化的主动配电网分布式电源优化配置方法[J]. 电力系统保护与控制, 2020, 48(15): 141-148.

LING Wanshui, LIU Gang. Distributed generation optimal configuration method for active distribution networks based on robust optimization[J]. Power System Protection and Control, 2020, 48(15): 141-148.

[31] 徐崇博, 杨晓东, 张有兵, 等. 考虑风险管控的含智能软开关主动配电网随机运行优化方法[J]. 电力系统自动化, 2021, 18(3): 1-15.

XU Chongbo, YANG Xiaodong, ZHANG Youbing, et al.Stochastic operation optimization method for active distribution networks with soft open point considering risk management and control[J]. Automation of Electric Power Systems, 2021, 18(3): 1-15.

[32] 卫志农, 陈妤, 黄文进, 等. 考虑条件风险价值的虚拟电厂多电源容量优化配置模型[J]. 电力系统自动化, 2018, 42(4): 39-46.

WEI Zhinong, CHEN Yu, HUANG Wenjin, et al.Optimal allocation model for multi-energy capacity of virtual power plant considering conditional value-at-risk[J]. Automation of Electric Power Systems, 2018, 42(4): 39-46.

[33] WANG J, WANG W, YUAN Z, et al. A chaos disturbed beetle antennae search algorithm for a multiobjective distribution network reconfiguration considering the variation of load and DG[J]. IEEE Access, 2020, 8: 97392-97407.

[34] WANG J, WANG W, WANG H, et al. Dynamic reconfiguration of multiobjective distribution networks considering DG and EVs based on a novel LDBAS algorithm[J]. IEEE Access, 2020, 8: 216873-216893.

[35] 刘晋源, 吕林, 高红均, 等. 计及分布式电源和电动汽车特性的主动配电网规划[J]. 电力系统自动化, 2020, 44(12): 41-48.

LIU Jinyuan, LÜ Lin, GAO Hongjun, et al.Active distribution network planning considering characteristics of distributed generation and electric vehicle[J]. Automation of Electric Power Systems, 2020, 44(12): 41-48.

[36] TULADHA R, SINGH J, ONGSAKUL W. A multi-objective network reconfiguration of distribution network with solar and wind distributed generation using NSPSO[C] // International Conference on Green Energy for Sustainable Development, March 19-21, 2014, Cape Town, South Africa. IEEE, 2014: 1-7.

Planning method of soft open point for an active distribution network considering conditional value-at-risk

WANG Jie1, WANG Weiqing1, WANG Haiyun1, WU Jiahui1, WANG Shuaifei2

(1. Engineering Research Center of Education Ministry for Renewable Energy Power Generation and Grid-connected Control, Xinjiang University, Urumqi 830047, China; 2. Huizhou Power Supply Bureau of Guangdong Power Grid Company, Huizhou 516001, China)

There are problems of voltage violations and branch overload caused by the high proportion of renewable distributed energy in a distribution network. Thus a three-layer planning model of soft open point (SOP) is proposed based on network reconstruction and conditional value-at-risk (CVaR) theory. First, in order to simulate the output uncertainty of distributed generation, an optimal scenario is constructed based on Wasserstein distance. Secondly, the upper layer model determines the location and capacity of SOPs considering the two objectives of minimizing the annual comprehensive cost and security risk simultaneously; the middle level model carries out network reconstruction with the goal of minimizing the running cost of each scene; in the optimization model of the lower layer, active various regulation measures such as on-load tap changers, switching capacitor banks, demand response and power transmission of SOPs are considered. In order to reduce the calculation complexity of the model, the hybrid method of the LDBAS algorithm based on grey target decision-making technology and second-order cone optimization is used to analyze the three-layer planning model. Finally, the proposed planning model is verified and analyzed by taking the modified IEEE 33 bus distribution system as an example.

This work is supported by the National Natural Science Foundation of China (No. 52067020 and No. 51667020).

active distribution network; soft open point; conditional value at risk (CVaR); capacity planning; grey target decision-making technology; LDBAS algorithm

10.19783/j.cnki.pspc.210412

国家自然科学基金项目资助(52067020，51667020)；自治区教育厅重点项目资助(XJEDU2019I009)

2021-04-15；

2021-06-24

王 杰(1990—)，女，博士研究生，研究方向为配电网优化、规划；E-mail: bjewang@163.com

王维庆(1959—)，男，通信作者，教授，博士生导师，研究方向为可再生能源并网、主动配电网规划、电力电子技术。E-mail: wangwq666@gmail.com

(编辑 魏小丽)