Image-denoising algorithm based on improved K-singular value decomposition and atom optimization
Rui Chen|Dong Pu|Ying Tong|Minghu Wu
1College of Information &Communication Engineering, Nanjing Institute of Technology,Nanjing, China
2College of Electric Power Engineering, Nanjing Institute of Technology,Nanjing,China
3Hubei Key Laboratory for High-efficiency Utilization of Solar Energy and Operation Control of Energy Storage System,Hubei University of technology,Wuhan,China
Abstract The traditional K-singular value decomposition (K-SVD) algorithm has poor imagedenoising performance under strong noise.An image-denoising algorithm is proposed based on improved K-SVD and dictionary atom optimization.First, a correlation coefficient-matching criterion is used to obtain a sparser representation of the image dictionary.The dictionary noise atom is detected according to structural complexity and noise intensity and removed to optimize the dictionary.Then, non-local regularity is incorporated into the denoising model to further improve image-denoising performance.Results of the simulated dictionary recovery problem and application on a transmission line dataset show that the proposed algorithm improves the smoothness of homogeneous regions while retaining details such as texture and edge.
1|INTRODUCTION
In the process of digital image acquisition and transmission,images are often contaminated by noise due to weather, light occlusion, and other reasons, which has a great impact on follow-up image processing.Image denoising,therefore,is one of the hotspots in image processing,and it remains a challenge for researchers because noise removal introduces artefacts and causes blurring of images.The main traditional approaches to image denoising include spatial filtering methods and transform domain filtering methods.Spatial filtering methods include non-local means[1],block-matching,and 3-D filtering(BM3D) [2].Transform domain filtering methods include wavelet transform [3, 4], curvelet transform [5], and Fourier transform[6].However,most traditional algorithms lose some image details while suppressing noise.Some algorithms combine transform domain filtering and spatial domain filtering but still have the problems of a complex algorithm,substantial memory use, and low efficiency.
Recently, sparse representation and dictionary learning have received extensive research interest and have been widely used in image-processing applications including image denoising [7-9], face recognition [10, 11], and image compression [12].Image-denoising methods based on sparse representation and dictionary learning mainly use the redundancy of the overcomplete dictionary to represent the image sparsely,which can effectively capture the structural features of the image and effectively preserve image information while eliminating noise.The authors in [7] proposed a K-singular value decomposition (K-SVD)-based denoising method with good performance removing mild noise.In a traditional KSVD sparse representation, dictionary training is a timeconsuming process, and the sparse decomposition mostly stops by setting a fixed hard threshold leading to loss of part of the effective content of the image [13, 14].
Addressing the above problems, the authors in [15]formulated image denoising as an optimization problem that can be iteratively solved by constructing a rank-sparsityrepresentation on a propagated dictionary.In[16],an improved K-SVD algorithm called sequential generation of K-means(SGK) [17] was proposed for sparse representation denoising, which has improved dictionary training time, but the denoising effect of this algorithm is similar to that of K-SVD,and the algorithm is complex.In [18], the authors provided a parameterized fuzzy adaptive way of adapting dictionaries.The update of the dictionary columns was combined with an update of the sparse representations by embedding a new mechanism of fuzzy set.For high-dimension data, Yi S et al.[19] presented an objective function including a robust reconstruction error term and a regularization term constrained by a Schatten-p norm and proposed a fast algorithm by eliminating the zero eigenvalues of the data matrix.To reduce the gap that exists between local processing and global image recovery,Romano et al.defined a disagreement-patch as the difference between the intermediate locally denoised patch and its corresponding part in the final outcome [20].To overcome the limitation of parameter adjustment in dictionary learning,[21]proposed a fully automatic Bayesian method that considered the uncertainty of the estimates and produced a sparse representation of the data without prior information on the number of non-zeros in each representation vector.To accurately restore the surficial information underlying largescale clouds, Li X.et al.[22] expanded the dictionary learning into two multitemporal,that is,K-SVD and Bayesian,counterparts.Furthermore,sparse representation models were analyzed in [23], and a model was proposed for recovering missing information in remote sensing images.These approaches greatly improve denoising performance,but it is still a challenge to deal with strong noise because the noisy image itself is used for training samples in the K-SVD denoising method.In addition,the K-SVD denoising algorithm based on dictionary learning only uses the inner information of the image block for independent sparse coding without considering the information related to other blocks, such as the overlap and similarity between blocks.Thus,it has insufficient ability to express prior information.Furthermore, sparse decomposition in overcomplete dictionaries is potentially an unstable problem and is prone to visual artefacts.
We propose a new image-denoising algorithm based on improved K-SVD and atom optimization in which the correlation coefficient matching criterion is combined with the dictionary clipping method.Considering the strong non-local self-similarity (NSS) of image blocks located at different locations, we introduce it into the image-denoising model as a regularized prior constraint.The flow chart of our proposed algorithm is presented in Figure 1.Compared with blockmatching and 3-D filtering (BM3D) [2], discrete cosine transform (DCT) [24], K-SVD [14], and SGK [25], our method retains important information such as edge and texture and has good denoising performance for processing power line inspection images.
The remainder of the paper is organized as follows.In Section 2, we review the denoising model based on sparse representation.The proposed algorithm with the derived solution is described in Section 3.The experimental results are given in Section 4, and conclusions are presented in Section 5.
2|IMAGE DENOISING ALGORITHM BASED ON K-SINGULAR VALUE DECOMPOSITION
2.1|Denoising model based on sparse representation
LetYbe the noisy observed image of sizeandXbe the unknown output denoised image. The image-denoising model can be established as [16]

whereλandμijare the penalty factors,Rijis ann×Nmatrix that extracts the (ij) block from the image of sizeD∈Rn×kis the dictionary withk>n, andαijis the sparse vector of coefficients corresponding to the (ij) block of the image.
Setting the initial dictionaryD, the sparse representation coefficientαijcan be solved by the orthonormal matching pursuit (OMP) algorithm [26] as

wherexijis the (ij) block of the unknown denoised image.DictionaryDcan then be updated by the K-SVD algorithm.Aftermiterations, the denoised image ^Xis obtained by Equation (3)

2.2|Dictionary optimization
When sparse coding, the sparse representation coefficie nts of signals under a given dictionaryDneed to be calculated.To obtain an adaptive dictionary, the noisy image itself is usually chosen as the training sample, leading to a contradiction between signal extraction and noise suppression.So we introduce a correlation coefficient matching criterion to extract a more meaningful training structure to obtain an optimal dictionary for more accurate image approximation.Furthermore, the training dictionary is optimized based on noise atom clipping.

F I G U R E 1 Flow chart of our image-denoising algorithm
In the sparse coding stage,the iterative stopping criteria of the dictionary learning methods are that the inner product of the residual and atom is less than the threshold value.When the noise intensity and the dimension of the overcompletedictionary become larger, the criterion terminates OMP [26]iteration prematurely, resulting in the omission of useful signals.The OMP algorithm is constrained by non-zero elements,and the dictionary atoms are selected greedily iteratively as

whereCis the noise gain,σis the noise standard deviation,andαijare the sparse representation coefficients.
To avoid premature termination of the algorithm,we adopt a weak selection iteration threshold[27]strategy,and the set of indices iswherekrepresents the current iteration, andTis a given threshold.We select any one element such thatwheregkis the correlation coefficient, which is the inner product of the residual and the column of sensing matrix.The weak selection iteration thresholdTkof the current iterationkiswhereais the weakness parameter such thata∈(0,1].The weak selection matching pursuit has good performance handling the iterating termination problem caused by the dimension of the overcomplete dictionary being infinite and the dimension of the inner product of the residual and the atom being finite.
As mentioned above,the dictionary trained by the K-SVD method contains noise atoms matched with noise, which results in the noise suppression process hindering the extraction of related signals.Therefore, it is necessary to delete these noise atoms from the dictionary as much as possible and optimize the dictionary.We use the Bartlett test [28] to detect noise atoms.Assuming thatνiis the variance of eigenvectors,the Bartlett test is used to test whether the variances of eigenvectors of atoms in four directions are equal or at least two atoms with different variances.The Bartlett test statisticQis defined as

wherenis the dimension of the dictionary atom.The random distribution of Gaussian noise makes the correlation of noise atoms in all directions almost zero.If an atom satisfiesQ<χ2(α:3), the atom can be considered to contain only noise and can be removed from the atomic library, whereχ2(α:3) represents theα-percentile position of chi-squared distribution with three degrees of freedom.Because only the noise atoms are deleted from the dictionary without affecting the information atoms, image-denoising performance can be improved.
3|PROPOSED ALGORITHM
As mentioned in Section 1, the K-SVD dictionary learning denoising method only uses the internal information of image blocks for independent sparse coding without considering the relevant information of the neighbouring images, so it has insufficient ability to express prior information.Meanwhile,sparse decomposition based on the overcomplete dictionary is a potential unstable problem.Therefore, it is necessary to introduce a regularization term into the denoising model.
3.1|Non-local similarity
Natural images usually contain many similar image blocks in local regions that are called NSS prior knowledge.Considering that image blocks can be used as multivariable vector samples,NSS priori training image blocks can be applied to dictionary learning based on sparse representation.Bcadls A et al.used the non-local similarity of image blocks for image denoising[29].The estimated value of the current pixel was obtained by the weighted average of the pixels with a similar neighbourhood structure in the image.The neighbourhood of the pixel to be denoised is used to represent its features for image restoration with the maximum possible number of image details.
Suppose the noisy image ispand the denoised image is^p;the central pixel value is thus
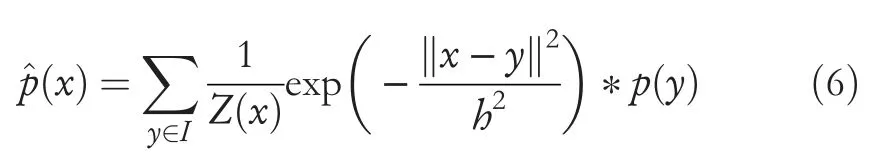
whereZ(x) is the normalized coefficient, andhis the control factor of the Gaussian kernel.The proposed algorithm hasgood denoising performance if the image is composed of a large number of similar blocks.However,in some specific areas with fewer similar blocks, denoising performance is not good,and robustness to noise is poor.Many approaches have improved the non-local mean image-denoising algorithm.To obtain more pixels or patches with higher similarity, Ji Z et al.[30] calculated the Zernike moments in the small local windows of each pixel in the image based on the similarity rather than the intensity of pixels.Zhang Q et al.[31]proposed a new framework that uses adaptive non-local energy to regulate the inverse linear imaging problem.A fast iterative algorithm was proposed for the regularization process to search similar image blocks and calculate weights.
3.2|Non-local regularization and atom optimization
We jointly exploit an image external patch prior and internal self-similarity prior and adopt an external patch prior-guided internal-clustering algorithm for image denoising.Zhang J.et al.[32] proposed a group-based sparse representation(GSR) to enforce intrinsic local sparsity and the NSS of images simultaneously.Li X.et al.[33] utilized local correlations in the temporal domain and non-local correlations in the spatial domain to efficiently exploit the non-local correlations owing to the patch matching of similar patches.Inspired by GSR, we adopt Gaussian mixture models(GMMs) to cluster similar patches.The learned GMMs from clean images are then used to guide the clustering of noisy patches of the input noisy images.The flow chart of the learning process of the patch group-based GMM prior model is shown in Figure 2.
The implementation process is as follows.
Step 1:Use K-means clustering method to train the natural images to obtainKgroups and then subtract the mean value from each patch group to obtain the non-local similar blocks.The reason for subtracting the mean is that after subtracting the mean value, the texture features of two patch groups with different texture features have a great degree of similarity, as shown in Figure 3.
Step 2: Combine the non-local similar patches and clustered groups.
Step 3:Train the non-local similar model again and extract the non-local similar patch groups.
Mahalanobis distance is used to measure the similarity of non-local block groups.For local-similarity patch group, the clustering method is guided by the prior knowledge, and the GMM learning method is used to obtain the local patch with high similarity.
When denoising the collected noisy imageY,the K-means method is used to introduce the prior information of the nonlocal patch group.Then,the GMMs are built to train the local patch groups, and the average value of the patch groups is calculated to measure local similarity.The similar patches are searched around the non-local patches, and the maximum average value of each similar patch is calculated.Finally, the non-local prior information is estimated from the transmission line image, and the sparse representation is used for the internal block.

F I G U R E 2 Learning process of patch group-based Gaussian mixture prior model

F I G U R E 3 Subtracting mean value of different patch groups (texture feature)
In sparse representation, the sparse coefficient vector conforms to the Laplace distribution,so the sparse coefficient vector can be weighted to obtain the weight vectorwherecis constant andσis the noise standard deviation.An adaptive regularization term[10]is added to the optimization term of the weighted sparse coding model.Adopting the prior knowledge in the model training process,the image blocks are searched and assigned weights asW=exp(-με2), whereμis a positive constant andεis the coding residual used to suppress image noise [16].
In the denoising stage, dictionary and regularization parameters can be obtained by training the Gaussian mixture model, while the weighted sparse coding model is used for image denoising.To make the weighted coding model more effective in removing Gaussian noise, the regularization term in the optimization term can use the prior model of the natural image to build the model.The orthogonal dictionary is obtained by image training,and then the local K-SVD dictionary is selected from the given image blocks adaptively.In the iterative process of dictionary learning,we calculate the coding residualsεand optimize the weightsW.The added non-local regularization term is

where ϑ is the regularization factor,ϑ‖Y-represents the constraint between the non-local estimation matrixWYand the original imageY,φis the definition constant,andτis non-local expectation among the weighted blocks.φ‖ω(α-τ)‖1represents the constraint among non-local similar blocks.The adaptive weighting of the estimation matrix and original image can improve the quality of image restoration.
In (1), only an overcomplete dictionary is used to sparsely reconstruct the internal information of the image.The details of the image are smoothed in the same way as the noise, and the effect of image restoration is not obvious.We reconstruct the image-denoising model by combining the K-SVD algorithm with NSS prior knowledge.Thus, we introduceωas a regularization constraint and obtain our image-denoising model as

The optimization solution of Equation (8) can be decomposed into two block-related sub-problems as


To solve (9), we need to initialize the estimation of the original image.Then we use the block coordination minimization method to solve this subproblem,which can be divided into two steps as follows.
Step 1.To solve Equation (9), an overcomplete DCT dictionaryDis initialized first.According to the knownXandD,we obtain the sparse representation coefficientsαijby sparse coding based on the OMP algorithm.The numerical optimal solution of the sparse coefficient matrix^αijis obtained by

Xis updated by

Therefore,the optimization problem to solve Equation(9)is turned to find the non-regularization term optimization problem of the sparse model and can be simplified as

Then dictionaryDandαijare updated by the improved KSVD algorithm.The details are described in Algorithm 1.

Algorithm 1 Dictionary atom optimization 1: Task: solution of (9)2: Initialization: initialize dictionary D(0)∈Rn×Kcomposed by overcomplete DCT basis,sparse vector α(0)ij, and noisy image Y with α=0.01;3: For J = 1,..., Jmax 4: Sparse coding using stWGP algorithm until■■gki■■<α maxj■■■gkj■■■5: Dictionary atoms are decomposed by singular value decomposition 6: Noise atoms are deleted by the Bartlett test to establish an optimal overcomplete dictionary ^D 7: End for
Step 2.To solve Equation (10), we first calculate the selfsimilarity weight matrixW.Then, substituting the updated sparse representation dictionary, sparse representation coefficient, and weight matrixWinto (14), we can obtain the estimated image matrix.The details are described in Algorithm 2:


Algorithm 2 Image reconstruction based on nonlocal regularization K-SVD 1: Task: solution of (10)2: Input: dictionary ^D and sparse representation coefficient ^α;3: For J = 1,..., Jmax 4: Residual ε=y-^x(0)5: Regularization factor ϑ=0 6: Wh ile J To improve image reconstruction quality, the binomial regularization parametersλin Equation (10) must be able to balance the precise term and concentrated sparse term adaptively.We build a centralized local discrete model using the Bayesian maximum a posteriori probability estimation method.The non-local redundancy of the image can be estimated by calculating the non-local similar blocks and updating the parameters dynamically.The objective function can be solved by the iterative constraint in the sparse constraint problem. Letθ=α-β, whereβis the estimation of the sparse coefficientsα.For a givenβ, the estimation ofθcan be expressed as The estimation term obeys the Gaussian distribution in the maximum prior probability as The estimation of sparse coding coefficientβand the sparse coding noise both meet the Laplace distribution.Similarly, assume further thatθmeets the Laplace distribution as whereθi(j) represents the element ofj-th iteration andσi,jrepresents the standard deviation ofθi(j).Substituting Equations (16) and (17) into Equation (15), we can obtainθyas Therefore,for a givenβ,sparse codingαcan be obtained by minimizing the objective function.The optimal solution of Equation (17) can be solved by using the iterative contraction algorithm as In this section,we conduct extensive experiments to verify the effectiveness of the proposed method and apply it to actual transmission line image denoising.The proposed denoising method is compared with BM3D[2],DCT dictionary[24],KSVD [14], and SGK [25] algorithms.In the first part, we perform a set of experiments on standard images to test the denoising performance of our algorithm.In the second part,we present experimental results on typical defects in an actual transmission line image such as strand breakage, wear, and bubble.Each image is contaminated artificially by adding zeromean white Gaussian noise at different variancesσ2.For convenience, the images are preprocessed into 512 × 512 black-and-white images, the window size is set to 8 × 8, and the number of atoms in the dictionary is 256. We use an overcomplete DCT dictionary as the initialization for all training algorithms.Sparse coding in the denoising process is realized via OMP.The parameters in our experiments are set as follows. (1) The iteration number of K-SVDJmax= 10; (2) The terminating threshold for OMPε=1.15σ, and the Langrage multiplierλ=; (3) The weakness parametera= 0.8; (4) The number of clusters = 5; (5) The training images are 200 images of transmission line of size 512 × 512. We use peak signal-to-noise ratio (PSNR) and structural similarity index (SSIM) as denoising criteria.We use DCT,K-SVD,BM3D,SGK,and the proposed algorithms to denoise imageLenawithσ=10.As we can see in the denoising results of the five algorithms from Figure 4(c)-4(g),the image's details are basically well preserved,but the denoising effects of SGK and our algorithm have clearer textural features in hair and brim.The quantitative results of the five algorithms for imagesLena,Boat,andPeppersare shown in Table 1 and are the average values of the five denoising results.The PSNR of our algorithm are superior to that of the others.The PSNR of SGK is similar to that of K-SVD,and it is superior to the DCT and BM3D algorithms.Our algorithm achieves better performance in terms of SSIM,which implies better perceptual quality of the denoised image. T A B L E 2 Comparison of differentmethods in PSNR and SSIM under different noise levels T A B L E 3 Average PSNR (in dB) results by different denoising methods under different noise levels F I G U R E 5 Denoising results with σ =20 on the image of broken strands on power line,(a)original image;(b)noisy image;(c)discrete cosine transform;(d) K-singular value decomposition; (e) block-matching and 3-D filtering; (f) sequential generation of K-means; (g) proposed F I G U R E 6 Denoising results with σ=25 on the image of worn power line,(a)original image;(b)noisy image;(c)discrete cosine transform;(d)K-singular value decomposition; (e) block-matching and 3-D filtering; (f) sequential generation of K-means; (g) proposed F I G U R E 7 Denoising results with σ = 50 on the image of bubbles power line, (a) original image; (b) noisy image; (c) discrete cosine transform; (d) Ksingular value decomposition; (e) block-matching and 3-D filtering; (f) sequential generation of K-means; (g) proposed T A B L E 1 Comparison of five algorithms in PSNR and SSIM with different noise levels F I G U R E 4 Denoising results with σ = 10 on image Lena, (a) original image; (b) noisy image; (c) discrete cosine transform; (d) K-singular value decomposition; (e) block-matching and 3-D filtering; (f) sequential generation of K-means; (g) proposed To evaluate the actual denoising performance of our algorithm, we have conducted experiments on a self-building dataset of a power transmission line collected from the unmanned aerial vehicle images.There are three types of power line defects, broken strands, worn power lines, and bubbles.The denoising results of the three defects are shown in Figures 5-7,respectively.We can see from Figures 5(g),6(g),and 7(g)that our algorithm can handle the edge-blurring problem in image recovery.For example,the textural feature in Figure 5(g)of the obscure part of the gully below the power line is recovered well compared with Figure 5(c)-5(f).Figure 6 displays the original,noisy,and denoised images of the worn power line withσ=25.As we can see from Figure 6(c)-6(f),there still exists worn edge blurring in the denoised image.As shown in Figure 6(g), our proposed algorithm has a good subjective detail recovery effect and solves the problem of feature blurring in the smooth part of the traditional algorithm.For the collected power line images with bubbles, Figure 7(c)-7(f) displays the denoised images using DCT, BM3D, K-SVD, and SGK algorithms,respectively.As we can see from Figure 7(c)-7(f), the details of the restoring image are lost under high noise.Our proposed algorithm can solve the problem of mistaking image information as noise under high noise,so the texture recovery is remarkable. The complete experimental data are shown in Table 2.As we can see from Table 2, for broken strands images, the denoising performance of all algorithms are good, our algorithm outperforms the other algorithms less than 1 dB in term of PSNR.For worn and bubbles images, our algorithm outperforms DCT algorithm 2~4 dB, BM3D algorithm 1~3 dB, K-SVD algorithm 1~2 dB, and 0.6~1.5 dB in terms of PSNR. In summary, the edge details of the reconstructed image using the proposed algorithm are clear under strong Gaussian noise, and the subjective visual effect is better.The proposed algorithm can solve the problem of blurring features at the smoothing point of noisy image and treating image information as noise.The PSNR and SSIM values of three typical defects were increased by 1.83 dB and 0.01,respectively.The proposed algorithm is more suitable for image denoising with strong Gaussian noise, and especially in practical transmission line applications, the denoising performance is better than that of experimental simulation. Furthermore, we have conducted experiments on eight standard image datasets and our self-building image dataset of the power line.The standard image datasets include three grey image datasets (Set12, BSD68, and RN16) and five colourimage datasets (CBSD68, Kodak24, McMaster, RNI15, and CSet8).In total, these datasets include 229 images.Our collected dataset includes 300 images of three defects(i.e.broken strands, wear, and bubbles).The average PSNR performance of DCT,BM3D,K-SVD,SGK,and the proposed method are tabulated in Table 3. T A B L E 4 Execution time of the different denoising methods Finally,the execution time of denoising 50 standard images with different methods is reported in Table 4 and is the average of 10 experiments. An image-denoising method is presented based on improved K-SVD and atom optimization that can be applied to strong noise.The proposed method not only considers image feature extraction and noise atom suppression but also introduces sparse coding based on correlation coefficient matching and iterative stopping criteria of an OMP algorithm based on weak selection iterative threshold strategy in dictionary training.The dictionary is optimized by tailoring the atomic library.Furthermore, considering the NSS of the image, a non-local regularization term is introduced into the denoising model.The experimental results show that compared with similar denoising algorithms, the proposed algorithm not only removes the noise in the smoothing area and reduces the wrinkle phenomenon in the smoothing area but also preserves details such as edge texture and can remove Gaussian noise in the transmission line image. ACKNOWLEDGEMENT This work is financially supported by Science and Technology Research Program of Hubei Provincial Department of Education (T201805), Major Technological Innovation Projects of Hubei (No.2018AAA028), National Natural Science Foundation of China (Grant No.61703201) and NSF of Jiangsu Province (BK20170765). ORCID Rui Chenhttps://orcid.org/0000-0001-7868-11153.3|Adaptive regularization term optimization

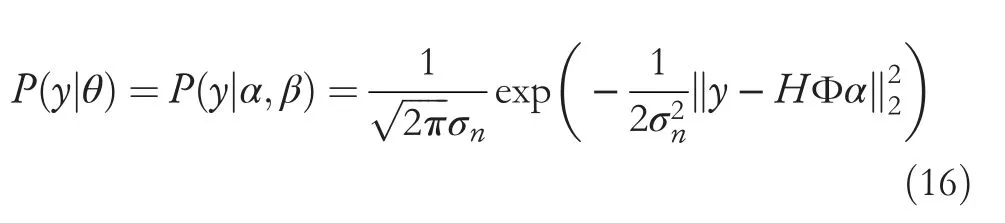
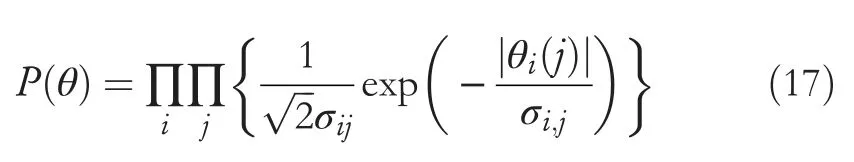

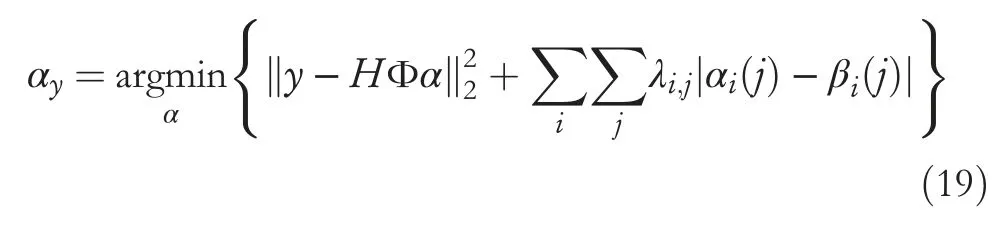
4|EXPERIMENTAL RESULTS








5|CONCLUSION
 CAAI Transactions on Intelligence Technology2022年1期
CAAI Transactions on Intelligence Technology2022年1期
- CAAI Transactions on Intelligence Technology的其它文章
- Stock values predictions using deep learning based hybrid models
- APPENDIX: BLOODY MAHJONG GAME RULES
- Bloody Mahjong playing strategy based on the integration of deep learning and XGBoost
- Shoulder girdle recognition using electrophysiological and low frequency anatomical contraction signals for prosthesis control
- Several rough set models in quotient space
- Improving data hiding within colour images using hue component of HSV colour space
