全国名校高二上学期期未押题卷（二）

冯连福 李燕燕

一、选择题（本题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。）

1.已知P为抛物线C：y2=2px（p》0）上一点，点P到抛物线C的焦点的距离为8，到y轴的距离为4，则卫=（）。

A.4

B.6

C.8

D.10

2.已知等比数列{am}的公比q》-1，且a1与a3的等差中项为5，a2=-4，则a2o22=（）。

为真命题的一个充分不必要条件可以是（）。

A.m∈（-∞，-3）

B.m∈（-∞，-2）

C.m∈（-∞，-2]

D.m∈（-∞，-3]

4.太阳神鸟金饰（如图1）是21世纪我国考古工作的一个重大发现，其图案设计之精妙令世人瞩目。國家文物局正式公布采用帝周太阳神鸟金饰图案为中国“文化遗产标志”。太阳神鸟金饰最突出的数学问题是如何运用尺规进行圆的+二等分，图2为用尺规+二等分圆周的作法，其中圆O上的黑点即为所作出的+二个等分点，若圆O的半径为1，则顺次连接这+二个分点所得的正+二边形的边长为（）。

5.已知圆锥S-OAB（如图3），轴截面△SAB是正三角形，C为圆O上一点，若∠BOC=，则直线SC与OB所成角的余弦值为（）。

6.已知命题p：若点A（x1，y1），B（x2，y2）都在函数f（x）=1-1nx的图像上，则点（x1x2，y1+y2-1）-定在f（x）的图像上;命题q：满足{3，4}UC={1，2，3，4}的集合C有16个。则下列命题为真命题的是（）。

7.已知实数x，y满足

所表示的平面区域为D，则下列结论中错误的是（）。

8.已知F1、F2为椭圆

9.如图4所示，在Rt△ABC中，∠C=90°，BC=3，AC=6，D，E分别是AC，AB上的点，且DEBC，DE=2，将△ADE沿DE折到△A1DE的位置，使A1C⊥CD，如图5所示。若M是A1D的中点，则CM与平面A1BE所成角的大小是（）。

10.设a，b均为正数，且（a-1）（b-1）=4。①a》1且b》1;②a2+b2+1》（ab-1）;③ab的最大值为9，当且仅当a=b=3时取得最大值;④α+b的最小值为6，当且仅当a=b=3时取得最小值。则下列各项正确的是（）。

A.①④

B.①②

C.3

D.①③④

11.若双曲线上存在四点，使得以这四点为顶点的四边形是菱形，则该双曲线的离心率的取值范围为（）。

A.（1，/2）

B.（1，3）

C.（2，+∞）

D.（/3，+∞）

则以上结论正确的是（）。

A.①②

B.2

C.③④

D.②③④

二、填空题（本题共4小题，每小题5分，共20分。）

13.已知空间四边形ABCD的每条边和对角线的长都等于a，点E、F分别是BC、

AD的中点，则AE·AF的值为

14.在△ABC中，角A，B，C的对边分别为a，b，c，∠ABC=120°，∠ABC的平分线交AC于点D，且BD=1，则4a+c的最小值为

15.已知抛物线y2=2x的焦点为F，准线为L，P是L上一点，直线PF与抛物线交于M，N两点，若PF=3MF，则|MN|=

三、解答题（共70分，解答应写出文字说明、证明过程或演算步骤。）

17.（本小题满分10分）已知卫：方程

（1）若卫为真，求实数t的取值范围;

（2）若p∧q为假命题，且卫Vq为真命题，求实数t的取值范围。

=0。从这三个条件中任选一个，补充在下面的问题中，并根据题意解决问题。

在△ABC中，内角A，B，C所对的边分别为a，b，c，已知

（1）求sinB;

（2）若b=22，求△ABC的面积的最大值。

19.（本小题满分12分）截至北京时间2021年11月30日，全球各国累计确诊新冠患者2.62亿，为支援某地抗疫，某工厂有100名工人接受了生产1000台某产品的总任务。每台产品由9个甲型装置和3个乙型装置配套组成，每名工人每小时能加工完成1个甲型装置或3个乙型装置。现将工人分成两组，分别加工甲型和乙型装置，设加工甲型装置的工人有x名，他们加工完甲型装置所需时间为t1，其余工人加工完乙型装置所需时间为t2，设f（x）=t1+t2。

（1）求f（x）的解析式，并写出其定义域;

（2）当x等于多少时，f（x）取得最小值？

20.（本小题满分12分）已知数列{am}满

（1）证明数列{am-2}为等比数列，并求ani

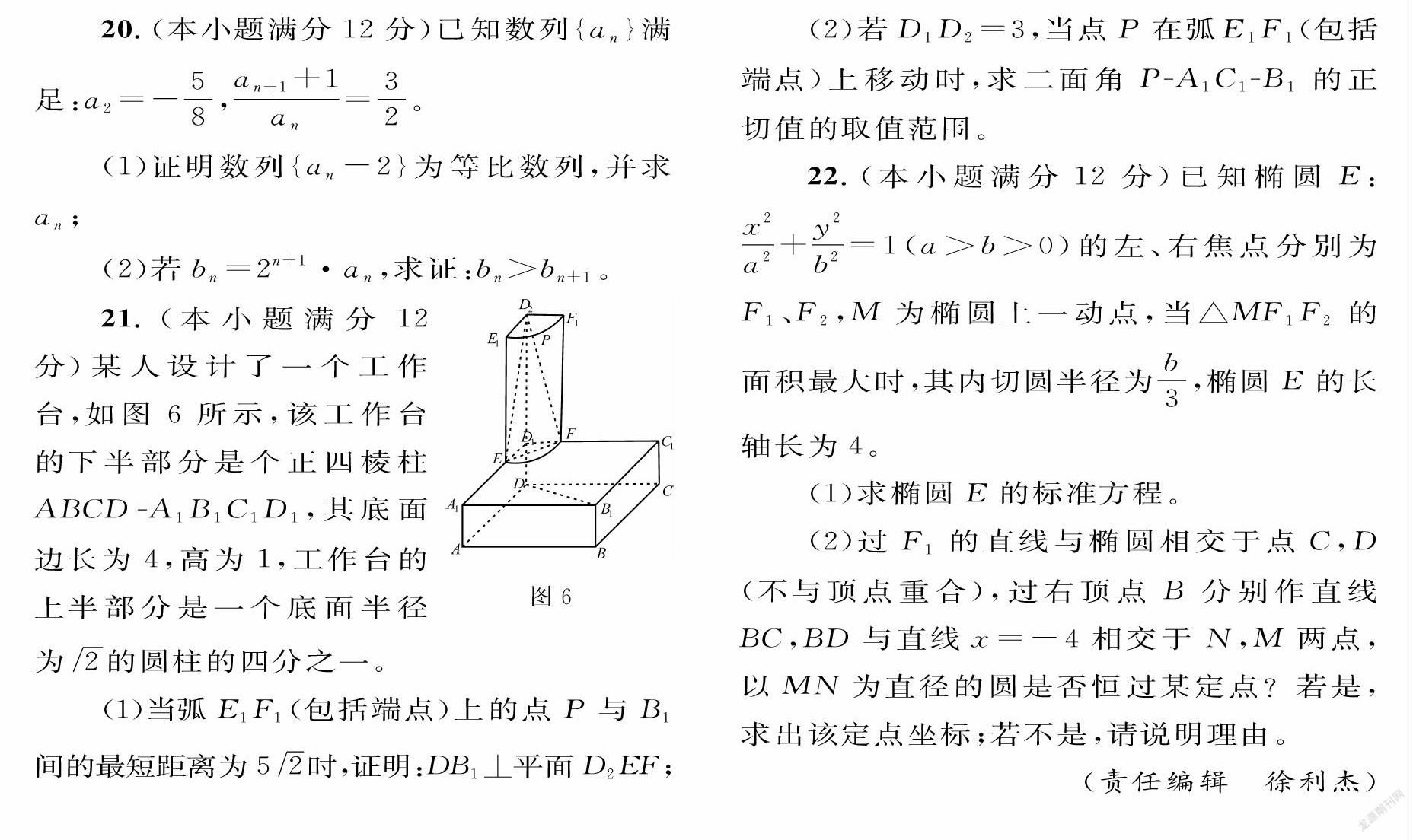
21.（本小题满分12分）某人设计了一个工作台，如图6所示，该工作台的下半部分是个正四棱柱ABCD-A1B1C1D1，其底面边长为4，高为1，工作台的上半部分是一个底面半径为/2的圆柱的四分之一。

（1）当弧E，F，（包括端点）上的点P与B间的最短距离为5/2时，证明：DB1⊥平面D2EF;

（2）若D1D2=3，当点P在弧E1F1（包括端点）上移动时，求二面角P-A1C1-B1的正切值的取值范围。

22.（本小题满分12分）已知椭圆E：

面积最大时，其内切圆半径为？，椭圆E的长轴长为4。

（1）求椭圆E的标准方程。

（2）过F，的直线与椭圆相交于点C，D（不与顶点重合），过右顶点B分别作直线BC，BD与直线x=-4相交于N，M两点，以MN为直径的圆是否恒过某定点？若是，求出该定点坐标;若不是，请说明理由。

（责任编辑 徐利杰）