结构-NFVD-TTMDI的控制性能

赵祥异 李春祥 曹黎媛

摘要：为了更好地发挥串并联调谐质量阻尼器惯容器（ Tuned Tandem Mass Dampers-Inerters，TTMDI）的优势，进一步提高其有效性和鲁棒性，使其能够广泛地应用于实际工程中，提出了连接阻尼器为非线性液体黏滞阻尼器的串并联调谐质量阻尼器惯容器（ Nonlinear Fluid Viscous DamperTuned Tandem Mass Dampers Inerters，NFVDTTMDI）。在频域内推导出结构NFVDTTMDI系统的动力放大系数半解析解，进而定义了NFVDTTMDI系统的最优化准则。采用迭代法进行等效线性化并使用FMINCON算法进行寻优，研究了不同阻尼指数v对NFVDTTMDI系统最优参数、减振有效性以及鲁棒性和质量块冲程的影响，并在时域内进行了验证。数值结果表明，相较于线性TTMDI，NFVD-TTMDI不仅具有相似的较高控制性能，而且当u

关键词：振动控制;调谐质量阻尼器;非线性液体黏滞阻尼器;惯质;等效线性化

中图分类号：TB535;TU311.3

文献标志码：A

文章编号：10044523（ 2022）01-005509

DOI： 10.1638 5/j .cnki.issn.10044523.2022.01.006

引 言

调谐质量阻尼器（ Tuned Mass Damper，TMD）是一种附加在主结构上的被动减振装置，其研究已有上百年历史。TMD的减振原理是：通过准确调整TMD系统的频率与阻尼参数，将主结构振动系统的能量转移到TMD并由其耗散，从而抑制主结构振动响应。目前，TMD已经在世界范围内广泛应用于柔性和低阻尼结构，如大跨度桥梁[1-2]和高层建筑[3]。

在TMD的基础上，许多学者针对新型TMD及其减振性能开展了研究。汪志昊等[4]提出摆式TMD频率调节方法，可以实现TMD频率的双向调节;罗一帆等[5]研究了电磁集能式调谐质量阻尼器的结构振动控制优化参数及其减振性能。为了进一步提高TMD的有效性和鲁棒性，多个TMD调谐控制的方法被研究提出[6-10]。而在Smith[11]提出惯质（Inerter，也称惯容）的概念后学者们开展了各种带有惯质的耗能减振装置研究，如调谐黏滞质量阻尼器（ Tuned Viscous Mass Damper.TVMD）[12]、调谐惯容器阻尼器（ Tuned Inerter Damper，TID）[13]、调谐质量阻尼器惯容器（ Tuned Mass Damper Inerter，TMDI）[14]、串并联调谐质量阻尼器惯容器（ TunedTandem Mass Dampers-Inerters. TTMDI）[15]。在上述研究中，连接阻尼器均假定为线性，但目前黏滞阻尼器市场以非线性黏滞阻尼器为主流，一般而言，非线性黏滞阻尼器的减振效果较线性黏滞阻尼器的更好，而且制作简易更为经济[16]。因此非线性黏滞阻尼器被许多学者进一步研究并应用到实际中[17，19];Huang等[20]提出了连接阻尼器为非线性液体黏滞阻尼器的TVMD，发现其可以获得和线性TVMD相当的控制效果，并能显著减少所需阻尼系数。

本文在此基础上提出了连接阻尼器为非线性液体黏滞阻尼器的串并联调谐质量阻尼器惯容器，研究了阻尼指数分别为0.2，0.5，1.0，1.5，2.0情况下的控制性能。针对非线性黏滞阻尼器，采用迭代法进行等效线性化寻找等效阻尼比。在迭代的过程中与优化同时进行，最终得到装置的最优参数和对应主结构响应。

1 结构-TTMDI系统的动力方程

单白由度结构-NFVD-TTMDI在简谐激励下的力学模型如图1所示。TTMDI包括两个质量块：TMD1和TMD2，它们通过各白的惯容器连接到地面;同时，在TMD1和TMD2之间设置一个连接阻尼器，该策略可以有效降低两个质量块的冲程大小，并且可以使系统的控制有效性进一步提高，此外设置连接阻尼器后会令c1和f2的阻尼系数为0，简化了系统，使得其更易于在实际T程中实现[15]。为便于与线性阻尼器区分，两个质量块之间的非线性液体黏滞阻尼器用红色表示。单白由度结构-TTMDI在简谐激励作用下的运动微分方程可以表示为：

通过公式（8）～（10）可以分别推导出从简谐激励到结构-TTMDI系统主结构、TMDI和TMD2的相对位移传递函数：

2 非线性液体黏滞阻尼器的研究方法

非线性液体黏滞阻尼器的阻尼力通常可以用以下方程来描述：式中 cd表示非线性阻尼器的阻尼系数，v表示阻尼指数，变化范围在0--2之间。v=0时表示摩擦阻尼器;而v=1时表示线性黏滞阻尼器，TTMDI即是NFVD-TTMDI在v=1.0时的特殊情况。

对于含有非线性黏滞阻尼器的系统，一般的研究方法是将非线性阻尼力转化为线性表达式，然后以线性系统的形式分析阻尼力。通过耗能相等定理[21]，简谐激励下非线性阻尼力可以用含等效阻尼系数Ce的线性阻尼力代替，Ce的一般表达式为[20]：

公式（20）表明，TTMDI的等效阻尼比取决于谐波激励的幅值、频率和未知的Rd。在这种情况下，Huang等[20]提出了迭代法來确定每一给定激励下的等效阻尼比和相应的Rd。图2显示了上述迭代方案的逐级流程图。值得一提的是，优化可以和迭代过程同时进行，即使用优化算法结合迭代方法来寻找最优参数。

3 数值分析

为对NFVD-TTMDI系统的参数f1，f2，ξ1，ξ2，Cd，η1进行优化，定义目标函数（即优化准则）为：

R=min .max.Rs s.t.Llb≤L≤Lub

（21）式中 L=[f1 f2 ξ1 ξ2 Cd η1]，Llb为参数取值下界，Lub为参数取值上界。目标函数式（21）表示：首先，得到目标函数（公式（13））中位移动力放大系数Ra的最大值，再在参数范围内，使最大的Rs最小化。目标函数代表了NFVD-TTMDI的减振有效性，目标函数值越小则有效性越高，优化算法通过该目标函数白动寻优得到装置的最优参数值。

数值模拟中，设定主结构的质量为ms=40 t，刚度为ka=2139.6 kN，因此白然频率为fn=1.164 Hz。简谐荷载的幅值P0=6000 N，激励频率的范围为Ofa～2fn。考虑目标函数式的复杂性，在MATLAB软件平台上采用多元约束优化算法（FMINCON函数）进行优化，优化参数及其范围如表1所示。

3.1 控制有效性

图3为在不同阻尼指数v和不同总质量比μ的情况下，NFVD-TTMDI主结构在频率范围内的最大DMF（ min.max.Rs）随总惯容质量比μI变化趋势。从图中可以看出NFVD-TTMDI的有效性对阻尼指数并不敏感，随着阻尼指数的增大，有效性略有提升，表明NFVD-TTMDI在阻尼指数大于1.0时可以实现比线性TTMDI更好的控制效果。此外，当μI值一定时，不同阻尼指数下NFVD-TTMDI系统的有效性都会随着μI的增大而提高，其主要原因在于惯容器增加了虚拟质量于控制系统中，极大地提高了其有效惯性质量，从而获得高效的控制效果。值得注意的是，当μI超过0.02时，增大μ对NFVD-TTMDI系统的控制效果的提升不再明显，而增大μI仍可以有效提高装置的控制效果。因此，适当的惯容质量可以使NFVD-TTMDI保持较高减振效果的同时，进一步减小质量块对质量的需求，从而达到控制系统轻质化。

3.2 最优频率比和最优阻尼系数

本节研究NFVD-TTMDI系统最优频率比和最优阻尼系数，表2给出了对于不同μ和v值，NFVD-TTMDI系统最优频率比和最优阻尼系数随μ1的变化趋势。从表中可以看出：当μ值一定时NFVD-TTMDI系统中最优频率比f1和f2随着μI增大而增大。此外还能看出不同阻尼指数下的f1几乎相等，而f2略有差异，在v=0.2时最小，在v=2.0时最大。由此可得出结论，NFVD-TTMDI系统的最优频率比对阻尼指数v不是很敏感，其中f2会随着阻尼指数的增大而略微增大。

另一方面，在NFVD-TTMDI系统中，TMDI和TMD2的最优阻尼系数均为零。主要原因是TMDI和TMD2所需求的阻尼都通过连接阻尼来实现。换而言之，连接阻尼代替TMDI和TMD2中的阻尼消耗了来白结构的能量，从而使得NFVD-TTMDI达到最优状态，因此利用该特性可以很好地简化系统。此外，NFVD-TTMDI系统所需的总阻尼系数随μI的增大而增大，随着μ减小而减小。不同阻尼指数情况下，所需阻尼系数随着阻尼指数的增大而增大。并且随着μI的增大，v< 1.0时最优阻尼系数增长趋势明显小于v≥1.0时的情况。由此可以得出结论：v< 1.0的NFVD-TTMDI系统可以显著降低所需阻尼系数，更容易实现，也更加经济。

3.3 质量块冲程

为了分析阻尼指数v对NFVD-TTMDI系统中质量块冲程的影响，定义TMDI和TMD2最大DMF（max.R1和max.R2）作为质量块冲程的评价准则。图4给出了对于不同μ和不同v值，NFVD-TT-MDI系统中质量块的冲程随μI的變化趋势。由图可知：由于附加惯容器的作用，NFVD-TTMDI系统质量块冲程随着μI的增大而显著减小;与此同时，NFVD-TTMDI系统中TMD1和TMD2质量块冲程几乎相等，分布比较均匀。NFVD-TTMDI中质量块冲程对阻尼指数v也不敏感，质量块TMDI和TMD2冲程随着阻尼指数的增大都略有增大。v

3.4 鲁棒性分析

由于结构特性的改变或对结构性质的认识不准确，NFVD-TTMDI系统可能会随着时间的推移而“失谐”。为此，对结构进行摄动，考虑对结构质量、刚度和阻尼的原始值分别均匀地缩放来评估NFVD - TTMDI的鲁棒性，缩放比例为80%-120%。为了便于比较，定义鲁棒性评价指标[20]：

LBX=（Rmax Rminmax） /Rminmax

（22）式中 Rminmax为原结构参数为msb kso，Cso情况下优化得到的主结构最小DMF。Rmax为仅改变主结构参数而NFVD-TTMDI装置参数不变情况下求得的主结构DMF。即用摄动后主体结构的最大DMF值相对于其最优值的增量来衡量外界条件发生变化时控制系统有效性的降低程度[20]。主结构参数摄动

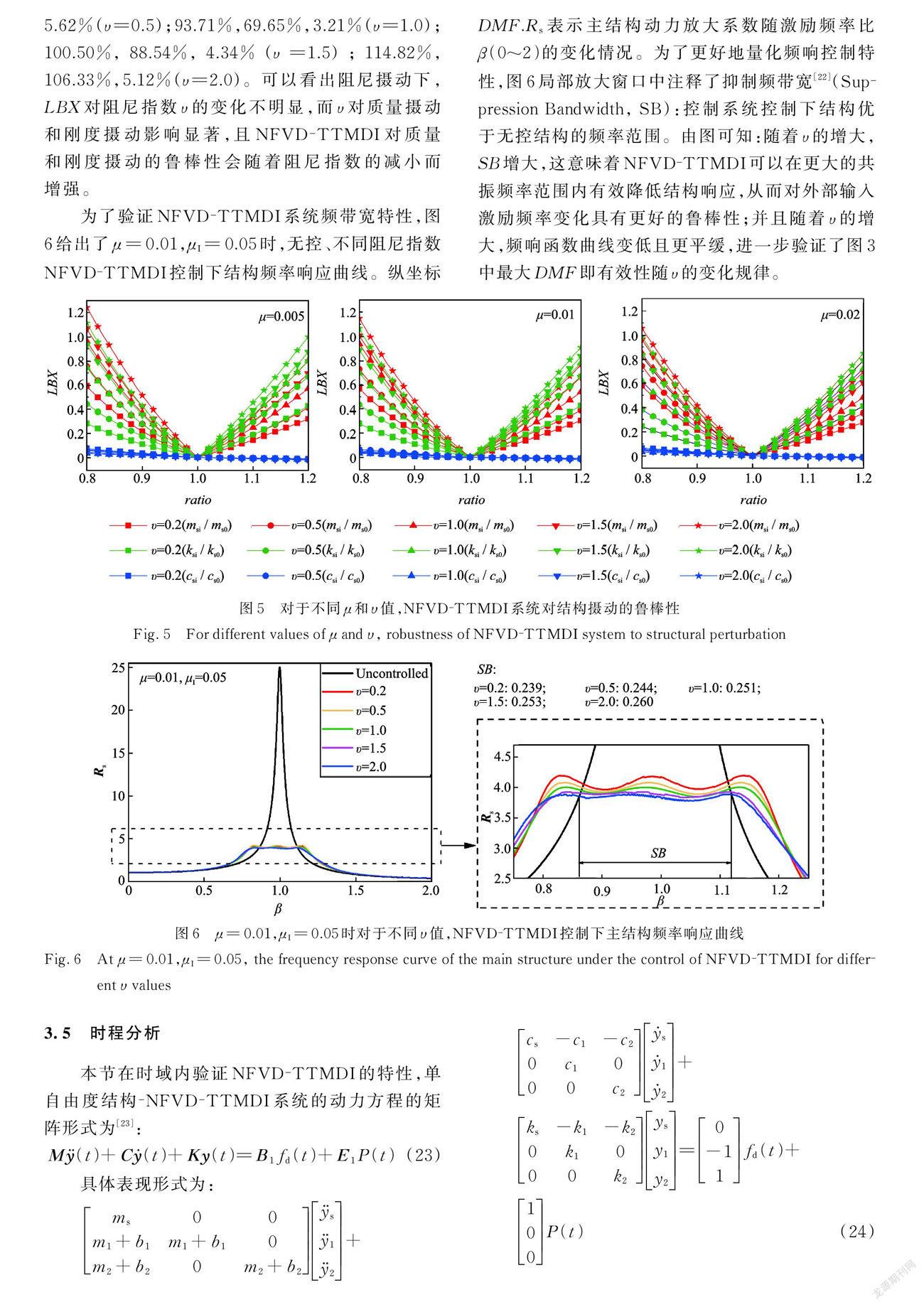
LBX越小，有效性降低程度越小，即NFVD-TTMDI对结构摄动的鲁棒性越强。图5给出了μI= 0.05，μ=0.005，0.01，0.02时，不同v情况下LBX随ratio的变化趋势。由图5可知：对于质量摄动和刚度摄动，缩放程度越小，LBX越小。然而对于阻尼摄动，LBX随着ratio的增大而减小。这是因为对阻尼来说，增大ratio相当于增加了结构阻尼，从而提高了结构的控制有效性。整体看来，结构对阻尼摄动的鲁棒性最强，例如当μ=0.01，ratio]=0.8时，对应质量、刚度、阻尼变化的LBX分别为：56.84% .27.62% .6.52%（v=0.2）; 72.76% ，43.36%，5.62%（v=0.5）;93.71%，69.65%，3.21%（v=1.0）;100.500/. 88.540/. 4.340/（v=1.5）;114.820/.106.330/，5.120/（u-2.0）。可以看出阻尼摄动下，LBX对阻尼指数u的变化不明显，而u对质量摄动和刚度摄动影响显著，且NFVD-TTMDI对质量和刚度摄动的鲁棒性会随着阻尼指数的减小而增强。

为了验证NFVD-TTMDI系统频带宽特性，图6给出了μ=0.01，μI= 0.05时，无控、不同阻尼指数NFVD-TTMDI控制下结构频率响应曲线。纵坐标DMF.Rs表示主结构动力放大系数随激励频率比β（0～2）的变化情况。为了更好地量化频响控制特性，图6局部放大窗口中注释了抑制频带宽[22]（Sup_pression Bandwidth，SB）：控制系统控制下结构优于无控结构的频率范围。由图可知：随着v的增大，SB增大，这意味着NFVD-TTMDI可以在更大的共振频率范围内有效降低结构响应，从而对外部输入激励频率变化具有更好的鲁棒性;并且随着v的增大，频响函数曲线变低且更平缓，进一步验证了图3中最大DMF即有效性随u的变化规律。

3.5 时程分析

本节在时域内验证NFVD-TTMDI的特性，单白由度结构-NFVD-TTMDI系统的动力方程的矩阵形式为[23]：

图7展示了μ=0.01，μI= 0.05时，图1所示系统在简谐激励P（ t）= 6000sin（t）sf作用下结构的位移响应时程曲线。模型参数和前文中一致，并利用在频域下得到的装置优化参数进行时域验证。由图可知：NFVD-TTMDI能有效地降低无控结构的位移响应。在振动初始，阻尼器刚开始起调谐作用，振动不稳定，在3s时 v=0.2，0.5，1.0，1.5，2.0时对应的主结构峰值位移响应分别为11.4，11.7，11.8，12.2，12.7 mm，意味着v<1.0时，非线性黏滞阻尼器能较快地起调谐作用，从而抑制结构振动。3s之后位移响应趋于稳定，v=0.2，0.5，1.0，1.5，2.0时主结构位移响应分为11.9，11.7，11.3，11.0和10.8 mm，说明振动稳定时阻尼指数越大，NFVD-TTMDI对结构的振动控制效果越好，与频域中的分析保持了一致。

4 结 论

本文提出了单白由度结构-NFVD-TTMDI系统。并推导出系统的动力放大系数半解析解，基于定义的目标函数，使用Fmincon算法在频域内研究了NFVD-TTMDI的减振性能，并通过离散化状态方程在时域内进行验证。得到如下的主要结论：

（1） NFVD-TTMDI可以实现与TTMDI相当甚至更好的控制效果，有效性会随着阻尼指数的增大而略微提高。

（2） NFVD-TTMDI和线性TTMDI同样仅通过连接阻尼消耗从结构中传来的能量，且在 v< 1.0时能有效降低所需阻尼系数，并且更好地抑制质量块冲程，有着更容易实现和更经济的优点。

（3）当结构摄动时，NFVD-TTMDI系统在v<1.0时可显著提高系统的鲁棒性。

（4）结构刚开始振动时，NFVD-TTMDI系统在v<1.0的情况下可以更快起到调谐作用，而当振动趋于稳定后，振动控制效果会随着阻尼指数的增大而提高。

综合考虑，NFVD-TTMDI可以获得与线性TTMDI十分相近的控制效果，但是可以在v<1.0时提高结构鲁棒性和降低所需阻尼系数，这些优势使得其在实际工程中更加经济有效。最后要说明的是研究NFVD-TTMDI连接单白由度结构，是为将装置应用在多白由度结构中打下理论基础，在之后的研究中会在多白由度结构中连接NFVD-TTMDI并添加风谱进行验证计算。根据实际工程应用，应将TMDI和TMD2设置在横向位移最大的楼层，一般是在最顶层。NFVD-TTMDI中各白的惯容器可通过设计足够大的板开口连接到结构的顶层以下一层或几层，通过不同的楼层跨度来研究装置的特性变化。可以预见的是惯容器跨越楼层数越多，由于较大的加速度增量，NFVD-TTMDI在减少结構振动方面的效率就越高。

参考文献：

[1]Fujino Y，Yoshida Y.Wind induced vibration and contr01 0f trans Tokyo Bay crossing bridge[J].Journal ofStructural Engineering，2002，128（8）：1012—1025.

[2]王浩，邹仲钦，茅建校，等.基于压重块型TMD的大跨度斜拉桥减震控制[J].振动工程学报，2018，31（3）：391 398.

Wang Hao，Zou Zhongqin，Mao Jianxiao，et al.Seismic contr01 0f a long span cable stayed bridge usingTMD type c.unterweight[J].Journal of Vibration En—gineering，2018，31（3）：391 398.

[3]Lu X，Zhang Q，Weng D，et al.Improving perfOrmance of a super ta11 building using a new eddy—currenttuned mass damper[J].Structure Contr01 and HealthM.nitoring，2016，24（3）：e1882.

[4]汪志昊，郜辉，张闯，等.摆式调谐质量阻尼器频率调节新方法[J].振动工程学报，2016，29（6）：1062 1069.

Wang Zhihao，Gao Hui，Zhang Chuang，et al.Frequency tunlng method in pendulum tuned mass dampers[J].Joumal of Vibration Engineering，2016，29（6）：10621069.

[5]罗一帆，孙洪鑫，王修勇.电磁调谐质量阻尼器的H2参数优化及对结构减震分析[J].振动工程学报，2018，31（3）：529 538.

Luo Yifan，Sun Hongxin，Wang Xiuyong.H2 parameters optlmlzation and vibration reduction analysis of electromagnetlc tuned mass damper[J].J.umal of Vibration Engineering，2018，31（3）：529 538.

[6]Jangid R S.Dynamic characteristics of structures withmultiple tuned mass dampers[J].Structural Engineering and Mechanics，1995，3（5）：497 509.

[7]Jangid R S.0ptimum multiple tuned maSs dampers fOrbase excited undamped system[J].Earthquake Engineering&Structural Dynamics，1999，28（9）：10411049。

[8]周晅毅，林勇建，顾明.大跨屋盖结构MTMD风振控制最优性能研究[J].振动工程学报，2015，28（2）：277 284.

Zhou Xuanyi，Lin Y.ngjian，Gu Ming.0ptimum pr.perties.f MTMD fOr large span rOOf subjected to wind10ads[J].Journal.f Vibrati.n Engineering，2015，28（2）：277 284.

[9]李春祥，韩兵康，杜冬.结构双重调谐质量阻尼器（DTMD）控制策略研究[J].土木工程学报，2005，38（5）：19.

Li Chunxiang， Han Bingkang， Du Dong. Control strategy of double tuned mass dampers for structures （DT-MD）[Jl. China Civil Engineering Journal， 2005， 38（5）：1 9.

[10]Yang Yunzhi， Li Chunxiang. Performance of tuned tandem mass dampers for structures under the ground accel-eration[J]. Structural Control and Health Monitoring，2017， 24 （10）：e1974.

[11]Smith M C.Synthesis of mechanical networks： the in-erter[J].IEEE Transaction Automatic Control， 2002，47（10）：1648-1662.

[12]Ikago K， Saito K， Inoue N. Seismic control of singledegreeof_freedom structure using tuned viscou.s massdamper[Jl. Earthquake Engineering&Structural Dynamics. 2012 .41（3）：453474.

[13]Lazar I F. Neild S A， Wagg D J.Using an inerter_based device for structural vibration suppression[Jl.Earthquake Engineering&Structural Dynamics， 2014，43（8）：1129-1147.

[14]Marian L. CJiaralis A. Optimal design of a novel tunedmassdamperinerter（ TMDI） passive vibration controlconfiguration for stochastically supportexcited structural systems[Jl. Probabilistic Engineering Mechanics，2014，38：156-164.

[15]Cao Liyuan， Li Chunxiang. Tuned tandem mass damp-ers-inerters with broadband high effectiveness for struc-tures under white noise base excitations[Jl. StructuralControl and Health Monitoring， 2019， 26（3）：e2319.

[16]Guo P F， Lang Z Q， Peng Z K. Analysis and design ofthe force and displacement transmissibility of nonlinearvi.scous damper based vibration isolation systems[Jl.Nonlinear Dynamics， 2012， 67（4）：2671-2687.

[17]黃政，刘子煜，周云，等.设计参数对非线性黏滞阻尼器的力学性能影响研究[J].工程抗震与加固改造，2018，40（5）：71-81.

Huang Zheng， Liu Ziyu， Zhou Yun. et al.Influence ofdesign parameters on mechanical properties of nonlinearvi.scous damper[Jl. Earthquake Resistant Engineeringand Retrofitting， 2018， 40（5）：71-81.

[18]陈建兵，曾小树，彭勇波.非线性黏滞阻尼器系统的刚性性质与动力时程分析[J].工程力学，2016，33（7）：204211.

Chen Jianbing， Zeng Xiaoshu， Peng Yongbo. Time-his-tory analysis and stiff properties of nonlinear viscousdamper systems[Jl. Engineering Mechanics， 2016， 33（7）：204211.

[19]韓建平，李晓松.基于性能的非线性黏滞阻尼器减震结构设计分析[J].建筑结构，2010， 40（ S2）：110-113.

Han Jianping， Li Xiaosong. Performance_based designand analysis of energydissipated structures with non-lin-ear viscous dampers [Jl. Building Structure， 2010. 40（ S2） ： 110-113.

[20] Huang Z， Hua X. Chen Z. et al. Optimal design of TVMD with linear and nonlinear viscous damping forSDOF systems subjected to harmomc excitation [Jl.Structural Control and Health Monitoring， 2019， 26（10） ：e2413.

[21] Soong T T， Constantinou M C. Passive and Active Structural Vibration Control in Civil Engineering [Ml. Vienna： Springer， 1994.

[22] Garrido H. Curadelli O， Ambrosini D. Improvement oftuned mass damper by using rotational inertia through tuned viscous mass damper[ J] . Engineering Structures ，2013 . 56 ： 21492153.

[23] Chung L L， Wu L Y. Yang C S W. et al. Optimal design formulas for viscous tuned mass dampers in wind excited structures [Jl. Structure Control and HealthMonitoring ， 2013 . 20（ 3） ： 320336.