考虑残余变形的震损框架结构性能评估及维修优化策略

何浩祥 程时涛 廖李灿

摘要：针对实际震损结构可测信息有限、修复加固过程难以模拟以及修复加固后结构性能不易评估的现状，建立梁柱构件端部曲率与顶部位移的关系，厘清残余位移、位移、曲率、损伤指数之问的关联，提出在有限元中模拟构件修复加固的方法和流程以及根据不同损伤物理量对构件损伤进行量化的方法。根据不同的损伤物理量以及修复策略对钢筋混凝土震损结构进行快速修复，对修复后的结构抗震性能进行评估并进行地震易损性分析。结果表明：对震损结构进行快速修复能够有效降低结构再遇地震时发生严重破坏和倒塌的风险;在不同的损伤物理量中根据残余位移角量化构件损伤，并指导震损结构快速修复能够最大限度提高结构抗震性能;相对于择件修复策略，择层修复具有更好的效果。

关键词：震损结构;损伤评估;修复加固;残余变形;易损性

中图分类号：TU312+.3;TU375.4

文献标志码：A

文章编号：10044523（2022）01-0023-11

DOI： 10.1638 5/j .cnki.issn.10044523.2022.01.003

引 言

在地震灾害中，建筑结构的破坏和倒塌是造成人员伤亡和财产损失的直接原因，因此结构的抗震设计、鉴定和性能评估具有重大意义[1]。震损结构是指在地震中发生损伤导致性能部分失效甚至倒塌的建筑结构[2]。在震后救援和结构功能恢复过程中，对震损结构的力学性能和损伤程度做出准确评估，并据此进行快速修复，能够有效提升结构的抗震性能，避免结构在余震中发生倒塌而造成更严重的人员伤亡和经济损失。此外，震损结构的快速评估和修复优化方案也是迅速恢复灾区结构使用功能，对灾民进行及时妥善安置的必要技术，成为区域抗震能力恢复中至关重要的环节。

良好的震损结构损伤性能评估方法不仅可以对构件和结构的损伤程度进行量化分析，还可以为结构修复加固方案和性能提升评定提供有效的指导和优化策略。目前对构件或结构的损伤程度进行评估除采用常用的层间位移角、顶点位移角、刚度变化系数、构件端部曲率和频率变化率等指标引之外，最具有代表性的是Park等[4]在對大量试验结果进行分析之后提出的由最大位移及滞回耗能线性组合而成的损伤评价指标，但其不能正确反映构件极限耗能随幅值变化的情况，同时存在阈值范围不严格、无法直接应用于结构动力时程分析等不足。虽然不同研究者提出了Park-Ang修正模型[5-6]，但仍不能完全改变其局限性。提出并应用准确而有效的构件和结构损伤指数是提升结构震害性能评价的关键。值得指出的是，上述损伤指标中的大部分通常是基于结构有限元模拟或试验来获取的，具有瞬时性，测量难度大，对于实际震损结构而言，如不能在地震过程中进行监测，并不能被准确有效地获取，这严重阻碍了实际震损结构性能评估的实现和普及。受制于目前震后检测的能力和手段，能够获得的震损结构性能指标一般仅包括裂缝尺寸和数量、构件和整体残余变形、构件破坏类型和数量等有限信息。能否及如何利用上述指标进行损伤评估，并结合有限元分析和传统评估方法提出切实可行的加固维修策略和优化方案是亟需解决的工程问题。

另一方面，对震损结构修复加固之后的性能进行准确模拟及分析，可为制定维修策略和结构易损性评估提供有效支持。由于震损结构中的部分构件已经发生不同程度的损伤甚至严重破坏，在加固维修模拟过程中，必须对各个构件的既有损伤信息进行有效保留，并对维修部分的构件实现材料和单元模型的有效更新才能准确计算其修复过程的真实性能，因此对震损修复结构进行合理的有限元建模和分析具有十分重要的研究意义。然而，在传统的结构有限元分析中一般只针对完好结构进行分析，或仅选取单根柱等典型构件进行局部修复模拟，极少涉及震损结构整体的弹塑性分析、修复加固模拟及综合评估，这极大阻碍了震损结构的性能模拟和加固维修优化策略研究，亟需发展相关的有限元分析方法。

此外，目前的震损结构维修加固研究主要考虑构件级别的新型修复加固技术和整体减震维修技术[7]，缺乏从力学机制、优化方法和经济效益等方面着手的系统深入的研究方法和成套技术[8]。基于实际工程能力和需求，在仅已知诸如构件和整体的残余变形及裂缝特征等可测的损伤性能参数之后，如果能够根据理论分析方法和工程经验进一步确定构件的最优维修顺序和技术方案，则可在有限时间内及时有效地提升结构抗震性能，为结构和区域的工程韧性提供有利支持。因此，研究震损结构的维修加固理论依据、择优策略及技术实现方法具有重要的理论和工程意义。

有鉴于此，本文从实际震损结构维修策略研究的迫切性出发，通过理论分析厘清了构件端部残余变形与位移、曲率和损伤指数之间的关系，提出以残余变形为主要参数的震损结构损伤评定思路和分析方法。针对目前有限元分析方法的不足，提出基于单元替换和重启动分析来实现震损结构修复加固的有限元模拟方法。在此基础上，考虑地震动主余震效应，按不同的损伤评价指标对受时间成本约束的震损结构快速修复方案进行全面细致的模拟，并对修复结构抗震性能进行分析，从而实现对不同快速修复方案的比较和择优。通过地震易损性分析获得了采用不同修复策略的震损结构加固前后产生损伤的风险，为实际震损结构的修复和加固提供建议和支撑。

1 框架结构变形参量与损伤指数关联性

1.1 构件端部位移、曲率和损伤指数的关系

对于钢筋混凝土框架结构，其抗震性能主要由钢筋混凝土柱和梁的性能决定[9]。对于震损结构，震后的柱和梁端部的最大变形和残余变形是评价其损伤性能的主要指标。作为构件和截面层面的变形量，位移和曲率均能够直接反映构件的材料特性、力学性能和损伤特征，因此通常采用力一位移或弯矩一曲率两种力学参量体系表征钢筋混凝土柱或梁的抗震性能和滞回能力。虽然构件端部的位移或变形较之曲率更直观且更易测量，但在理论和有限元分析中也经常使用截面曲率来表征损伤，因此需要从理论上建立二者之间的联系以便为震损评定提供统一的标准。在弹塑性状态下，构件的变形可以近似看作构件端部塑性铰区域的转动，通过建立框架结构梁柱构件顶部位移与端部曲率的关系，便可根据构件顶部位移计算得到相对应的端部曲率。gzslib202204041633

钢筋混凝土悬臂柱在轴向力N和水平力P的共同作用下产生变形，如图1所示。当构件进入弹塑性状态时将产生损伤，柱子以塑性铰区域为中心发生转动，其顶部位移“为屈服位移uy和塑性转动位移up之和，同时RC柱的端部曲率φ为屈服曲率φy和塑性曲率φp之和，且可近似认为φy沿柱高H线性分布而φp存在于塑性铰区域并均匀分布。因此，端部曲率φ和顶部位移u的关系可表示为：

此外，Priestley等[11]通过大量试验认为塑性铰长度与构件高度H以及纵筋直径d有关，并提出等效塑性铰长度表达式为：

lp=0.08H+6d

（4）

综上，通过联立式（1）～（4），钢筋混凝土悬臂柱在弹塑性状态下的端部曲率φ与顶部位移u之间的关系为：

一般情况下，塑性铰长度lp远小于柱高H，因此式（5）可以简化为：

框架结构中梁柱构件的边界条件与悬臂柱边界条件存在一定差别，可利用反弯点法将梁或普通层的柱拆分为两个相同的悬臂柱，并对式（6）进行修正，则其端部曲率与顶部位移之间的关系为：

底层柱的反弯点一般位于2/3柱高处，可以按同样方法进行修正，不再赘述。由以上结果可知梁或柱的顶部位移和端部曲率具有明确的线性关系，力一位移或弯矩一曲率两种力学参量体系是相通和内洽的，可以互相转换。

构件的耗能能力和抗震性能指数一般也通过以上两种力学参量体系来表征。例如，构件延性系数也可以用曲率延性系数和位移延性系数描述，对于普通钢混柱，二者近似关系如下：

在构件地震损伤评价中，可采用Park等[4]提出的考虑变形和滞回耗能的双参数模型（即Park-Ang模型）进行分析，其基本公式如下：式中 D表示构件的损伤值;dE表示构件的塑性耗能增量;um表示构件在地震作用下的实际位移;us表示构件在地震作用下的极限位移;Fy表示构件屈服力;β表示权重系数，其取值范围一般在0.10 --0.85之间。

Kunnath等[12]对Park-Ang模型进行改进，提出基于弯矩一曲率的损伤评价模型，公式如下：式中 φm表示构件在地震作用下的实际曲率;φs表示在地震作用下的极限曲率;φy表示在地震作用下的屈服曲率;My表示屈服弯矩;β的含义与Park-Ang模型中相同，表示权重系数。

由上两式可以看出，基于Park-Ang模型的损伤指数受位移比和能量比两项因素的影响。对大部分构件而言第一项的影响较大，损伤指数与位移之间呈近似线性关系，但受第二项能量比的影响，最终损伤指数随位移变化呈上凹型幂函数关系（阶次大于1）。

此外，何浩祥等”J基于弹塑性耗能差的概念认为结构的损伤程度可以由结构理想弹性状态耗能和实际耗能的差值与理想弹性耗能的比值来确定。如图2所示，假定构件或结构在弹性状态下的刚度为ke，其屈服荷载和屈服位移分别为Fy和uy，当进入塑性状态后，其屈服刚度系数为a。当位移为um时，构件或结构所受荷载为Fm，割线刚度为km。此时，构件或结构在理想弹性状态下和实际弹塑性状态下的耗能差值为三角形ABC的面积。由此，提出单调力下构件或结构的损伤指数公式如下：

文献[14]通过对梁柱节点进行拟静力试验验证了基于弹塑性耗能差的损伤评价模型的准确性。由理论和试验结果可知，基于弹塑性耗能差的损伤指数与位移之间存在上凸型幂函数关系（阶次小于1）。此外，Kratzig损伤模型[15-16]和等效黏滞阻尼比的演变趋势14均与基于弹塑性耗能差的损伤模型的类似。可见，尽管損伤指数和结构位移之间具有强相关性，但由于各损伤模型机理和内涵不同，各损伤指数与位移的关系函数存在一定区别，在震损评估时应选择更严谨准确的损伤模型。

1.2 构件端部残余变形与位移的关系

值得指出的是，曲率、位移等参数可以在有限元分析中直接获得，滞回曲线、延性系数和损伤指数等也可通过计算公式得到，并为结构损伤评估提供重要依据。然而对于真实震损结构而言，如果不进行性能监测，在震后仅能得到构件裂缝及残余位移等有限信息，与顶部位移和端部曲率相关的损伤评价指标在实际震损结构性能评价中受到了制约。考虑到裂缝产生机理的复杂性及随机性，建立震后残余位移和残余曲率与位移和曲率过程量及损伤指数的关系更可行，可为震损结构的损伤程度和性质提供直接依据，相应的理论和工程意义也更突出。

结构或构件在经历地震作用或往复加载后，由于刚度退化的缘故在卸载时会有不同程度的残余位移。朱伯龙[17]在三线型滞回曲线模型的基础上分析了构件在近屈服点和近极限点处的滞回环刚度退化规律，得到如下式所示的卸载刚度kT的表达式，并认为从屈服滞回环刚度ky到极限滞回环刚度ku之间的刚度退化随位移u的绝对值增加而发展。式中 u，uy和uu 分别表示结构或构件的位移、屈服位移以及极限位移。

通过卸载刚度kT，位移u以及与位移u相应的荷载P，即可求得从位移u处开始卸载后的残余位移ut，其计算公式如下：

ur=u-P/kT

（13）

日本的《公路桥梁抗震规范》[18]引根据Takeda模型以及多次试验得到的弯矩一曲率曲线，给出了钢筋混凝土构件在任意时刻t处的卸载刚度kT，其具体计算公式如下式所示：

同时在阪神地震之后，将对残余位移的限制要求首次写入抗震规范中，并给出如下式所示的桥墩残余位移简化计算方法：。

上述两组公式分别从力一位移、弯矩一曲率两种力学体系提出计算残余位移的方法，并能够通过残余位移反推得到相应的位移和曲率。由上文可知构件端部曲率与顶部位移具有线性函数关系，且可互相换算。因此可根据残余位移计算结构或构件位移和曲率，并通过位移获得损伤指数，从而量化结构损伤程度。

2 结构震损动态评估方法

如前文论述，对于未采用监测手段的实际震损结构来说，其损伤评估一般只能通过观测震后表观裂缝和残余位移并结合相关鉴定和检测规范进行定性或定量判断来实现，如果在震前已获取结构无损频率，也可以通过地震前后结构的频率变化来确定结构的损伤程度。除以上数据之外，很难获取更丰富的信息。通过结构弹塑性有限元模拟对结构在地震下的损伤演变和特性进行仿真既可以预测结构的损伤位置和程度，也可以为结构的维修加固提供有效的指导。由于在结构有限元时程分析中可以提取全面的结构响应信息，因此可以运用传统的损伤指数和分析方法来完成基本的损伤评估。然而，传统的损伤指数存在诸多不足：以最大层间位移角或最大顶点位移角为代表的极值型指标并不能反映结构的损伤演变过程，也不能表征具体构件的损伤情况;以Park-Ang损伤指数[4]和Kratzig损伤指数[15]为代表的组合累积型指标限于周期滞回耗能的假设在动力时程分析中无法有效应用，且存在阈值不严格等局限。建立准确有效的损伤指数是对震损结构及修复结构进行损伤评估的必要手段。gzslib202204041633

针对目前动态损伤评价方法存在的缺陷，何浩祥等[13]提出基于弹塑性耗能差的结构动态损伤指数，计算公式如下：

试验和数值模拟得到的结果表明基于弹塑性耗能差的结构损伤指数具有准确度高、阈值严格、动态表征、适用于多种构件和结构整体等优点。根据崔济东等[19]建议的结构不同损伤程度对应的位移角限值，将与位移角限值对应的耗能差损伤指数划分到同一损伤等级，由此得到如表1所示的结构不同损伤程度所对应的耗能差损伤指数取值范围。

上述方法能够反映具体地震动下的结构损伤演变过程。结构地震易损性分析[20-21]则能够展现在一定地震动强度和随机性下结构地震反应超越某种极限状态的概率，从而反映在不同地震动强度下结构的破坏程度。综上，对结构有限元模型进行大量时程分析，并将损伤计算方法和地震易损性分析结合才能实现精准的结构损伤评估和预测。某一确定地震动强度指标值下结构性能的超越概率可表达为：式中 DMlim表示该状态下结构响应或损伤指数的限值;DMmd为结构响应或损伤指数中位值;β表示易损性函数的对数标准差。

综上，本文建议将基于弹塑性耗能差的结构损伤指数作为评估结构震损破坏程度的依据，并应用于结构地震易损性分析，以定量反映结构发生不同程度破坏的超越概率。同时，通过比较震损结构修复前后以及不同修复方案下的地震易损性曲线特征来评价不同修复方案的优劣，为震损结构的实际修复提供指导。

3 基于有限元模拟震损结构修复加固流程

受限于经济成本，大批量制作框架结构试件并进行震损后的加固性能试验较难实现。为了在有限元中准确模拟震损结构经过部分修复加固后的抗震性能，首先要在有限元中对结构先施加地震作用使结构产生损伤成为震损结构，随后对震损结构中所有构件的损伤程度进行量化，最后根据量化结果对损伤严重的梁柱构件进行性能恢复以模拟修复加固效果。然而，大部分传统有限元软件并没有模拟该过程的功能。目前利用有限元软件模拟加固后结构抗震性能的研究较薄弱且主要是针对构件进行的，对于结构整体抗震性能模拟分析的研究较少。针对这些问题，提出一种在有限元中切实可行的修复加固模拟方法。

本文利用开源有限元软件OpenSEES来实现模拟震损结构修复加固的过程。在OpenSEES软件中常通过删除构件单元这一命令模拟框架结构中梁、柱构件损伤失效，引起结构内力重新分布，导致结构连续倒塌的动态过程。而实际震损结构中损伤构件的修复过程从一定角度可以理解为是原损伤构件拆除和新构件建立的过程。因此，为在有限元软件中实现震损结构修复这一过程，在OpenSEES中将删除单元和建立单元这两个功能相结合，通过单元替换的方式实现对震损结构中损伤构件的修复与加固过程，其具体流程如图3所示。

精准的震损结构损伤评估应该对所有构件的损伤程度进行综合评价，在修复加固时也宜从构件层面着手，通过对损伤构件进行精细修复使结构的使用功能得以恢复。因此，需要根据构件损伤指数对构件损伤程度进行量化，判断是否需要修复并选择合理的修复加固方式。随后，通过删除单元命令将损伤构件单元删除，在原损伤构件单元的节点上新建单元，并根据修复时所采取的材料设置新建单元的材料属性。另外，也可通过增加防屈曲支撑等耗能构件单元提高修复结构的抗震能力。

4 損伤表征指标及震损结构快速修复策略

对构件损伤进行评估量化的常用物理量指标包括最大位移角、残余位移（角）、端部曲率、刚度变化系数、频率变化率等。大量研究者围绕不同的表征损伤物理量指标给出了代表不同损伤程度的规定限值。如崔济东等[19]通过大量试验求得了RC梁、柱及剪力墙等在不同破坏程度时所对应最大位移角限值，为根据最大位移角对构件损伤进行量化提供理论依据。

受荷载作用方向以及配筋等因素的影响，构件在两个主轴方向上的震损程度并不相同。本文建议按以下公式对各损伤表征指标进行综合处理后再进行损伤评估。

等效最大位移角θm的计算公式为：

裂缝作为构件损伤最直接的反映，其数量和宽度能直接表征损伤程度。为对震损结构中所有梁柱构件损伤程度实现更全面充分的量化，建议将裂缝与表征损伤的物理量指标结合使用，计算公式如下：式中 d ir表示所有梁柱构件中第i个构件第7-条裂缝的宽度;Si表示根据表征损伤物理量指标对第i个构件的损伤量化值;Smax表示所有梁柱构件根据表征损伤物理量指标进行损伤量化中的最大值。

在基于有限元模型进行结构整体损伤评估时，也可采用刚度变化系数22和频率变化率[23]等指标来实现，其特点是考虑了完好结构与震损结构的性能差异。刚度变化系数的计算公式如下：

由于结构的频率与刚度相关，因此频率变化率是结构损伤的直接表征。何浩祥等[24]提出基于基本频率变化的时变损伤指标及相关有限元分析方法，以反映结构在地震作用下任意瞬时的损伤程度及演变过程，其计算式如下：

D（t）=1- [ To/T.（t）]2=1 = [f0（t）/f0]2（23）式中 T0和f0分别表示结构在弹性状态下的周期和频率;Te（t）和fe（t）分别表示结构的塑弹性时变周期和弹塑性时变频率。对于结构有限元模型，可通过提取结构质量矩阵和瞬时刚度矩阵并进行特征值分解来获得瞬时频率;对于有监测信号的实际结构，可以通过小波包分解或短时傅里叶变换等信号处理技术来提取结构的瞬时频率。

综上，在无监测的实际结构震损评估中，可以将残余位移（角）和裂缝特征作为损伤表征指标，对有监测的实际结构，可将最大位移角、端部曲率、刚度变化系数、频率变化率等作为补充指标。在有限元分析中，可以将基于弹塑性耗能差的损伤指数作为构件或结构级别的损伤评估指标，而将频率变化率或刚度变化系数作为整体损伤评估指标。

在地震发生后，为保障抗震救援的顺利开展，亟需在较短时间内对诸如医院等关键震损结构进行快速修复加固以使其恢复部分或全部使用功能，从而保证结构在遭遇余震时具有一定的抗震能力。由于机理有所区别，采用不同的损伤表征指标对震损结构梁柱构件损伤进行量化时，得到的构件损伤程度排序并不一致。因此，需要比对分析并筛选出能够最大限度提高震损结构抗震性能的损伤表征指标，并以此为依据指导震损结构的快速修复加固，进而形成优化策略。震损结构需要实现的优化目标或策略为：在仅修复加固有限个损伤梁柱构件的前提下能够最大限度地提升震损结构抗震能力。gzslib202204041633

针对震损结构的快速修复加固，通常存在两种不同的基本策略：一种是直接对结构整体中损伤最严重的楼层或构件群进行修复以保证其不会丧失使用功能（即择层修复）;另一种认为需要对每一层中损伤严重构件均进行修复（即择件修复），以防止刚度突变发生薄弱层转移的现象。两种修复加固策略均具有相应的理论基础，在指导震损结构快速修复时的效果优劣尚需要进一步研究和探讨。

5 实例分析

为验证在OpenSEES中通过单元替换模拟结构修复加固过程的可行性和准确性，选择一个二维弹性混凝土门式框架结构进行验证。结构模型如图4所示，梁、柱截面尺寸分别为0.25 m×0.50 m和0.50 m×0.50 m，弹性模量为3.0×10⁴MPa。对结构进行地震时程分析，随后对单元1进行单元替换并再次输入地震波进行时程分析，分别比较在不替换单元、替换单元但不修改彈性模量、替换单元且将弹性模量设为原来2倍或0.5倍这四种T况。主要分析顶点3处的位移响应，结果如图5所示。

由节点3的结果可以看出：在不替换单元和替换单元但不修改弹性模量两种T况下得到的节点3处位移时程完全一致;在替换单元并将弹性模量分别设为原来0.5倍和2倍后，位移变化则分别大于、小于不替换单元时节点3处的位移变化。由此可见，通过单元替换可以准确模拟损伤构件修复后的效果，这为分析震损结构修复加固后的性能提供了技术支持。

下面对比分析按不同的损伤表征指标指导修复有限个构件后对震损结构性能的提升程度，从而为实际震损结构快速修复加固提供理论指导。以7度区某5层钢筋混凝土框架结构作为研究对象。结构的平面布置如图6所示，结构层高3.3 m，混凝土强度C30，梁、柱截面尺寸分别为：250 mm×500 mm，500 mm×500 mm，梁、柱配筋率分别为：1.96%，1.57%。在OpenSEES中建立该混凝土框架结构模型，其中混凝土和钢筋的本构模型分别选用Con-crete01和Steel01，单元类型选用纤维单元。选用最大峰值加速度（PGA）为0.3g的El Centro波作为地震输入，使框架结构产生损伤成为震损结构。

取最大位移角、残余位移角、曲率和刚度变化系数作为损伤表征指标，并根据式（18）-（23）对所有构件的损伤程度进行量化，结果如图7所示。可以看出按不同损伤表征指标对构件损伤进行量化时得到严重次序并不一致，因而待修复的构件也不相同。

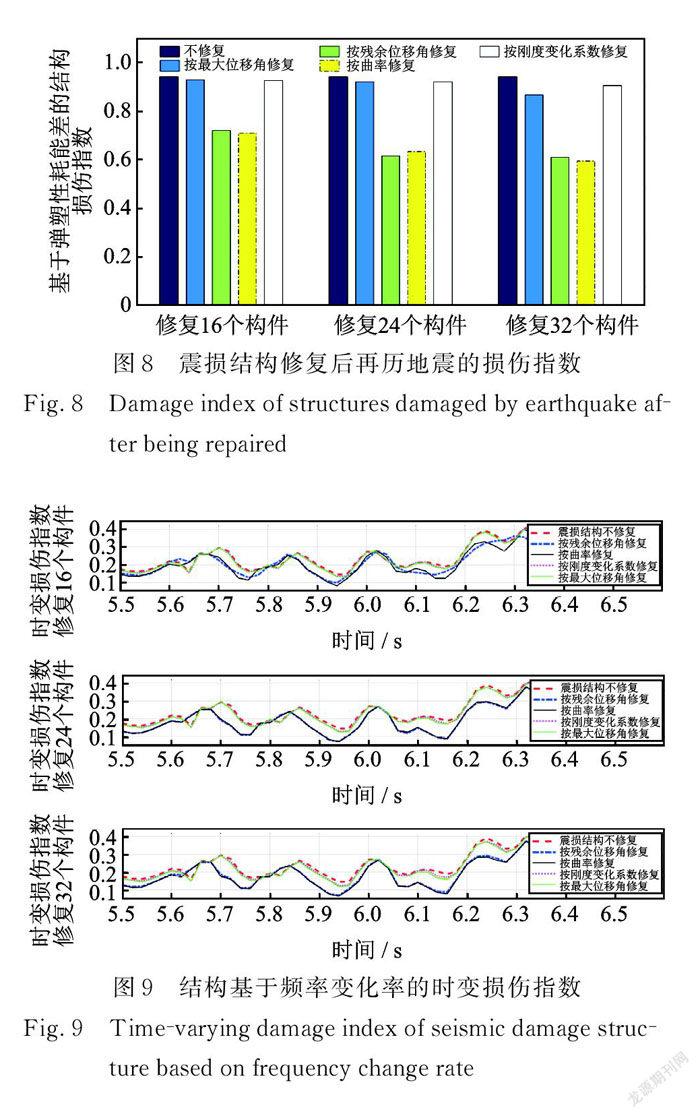
根据损伤量化结果，以单元替换的方法分别对震损结构中损伤最严重的前16，24和32个柱构件进行修复。随后输入PGA为0.3g的El Centro波，根据基于弹塑性耗能差的损伤评估方法对震损结构修复加固后再遇地震时的整体损伤程度进行量化，以对比不同损伤表征指标指导震损结构修复的效果优劣，得到的结果如图8所示。此外，在地震作用下，不同修复方案下用频率变化率表征损伤演变曲线如图9所示。

由图8可以看出，以残余位移角和曲率作为损伤表征指标指导震损结构快速修复后结构整体损伤指数最小，抗震性能最优，而其他指标对应的结果并不理想。同时，随着修复损伤构件数量的逐渐增多，震损结构在余震下的整体损伤指数逐渐降低，抗震性能得到逐步提高。由图9也可以看出按残余位移角和曲率指导震损结构修复后，余震下的损伤程度最小。

将曲率和残余位移角作为损伤表征指标，分别按择层修复和择件修复两种策略修复16，24，32个柱构件，并输入PGA为0.3g的El Centro波，分析不同修复策略对其抗震性能的影响。得到震损结构修复后再历地震时的整体损害指数如图10所示。

可以看出尽管根据两种策略对震损结构进行修复都能极大提高结构的抗震性能，但按择层修复策略修复后表现出更好的效果。因此，在对震损结构进行快速修复时，宜直接对结构整体中损伤最严重的楼层或构件群进行修复使震损结构修复后具有更好的抗震性能。

为进一步分析按不同损伤表征指标指导震损结构修复后的抗震性能，同时分析震损结构修复后遭遇地震时产生不同程度损伤的概率，以上文五层钢筋混凝土框架为例，取12组地震波记录作为地震输入进行结构地震易损性分析。将PGA和基于弹塑性耗能差的损伤指数分别作为地震动强度指数和结构损伤评估指数。考虑修复24个柱构件的情况，按式（16）分别计算PGA从0.1g提高至1.0g时结构的损伤指数，并按式（17）计算完好结构、震损结构、震损结构按曲率修复构件、按残余位移角修复构件以及按残余位移角和曲率加权统一修复构件后的地震易损性。其中，加权统一修复是指对于遭受不同地震作用的12个工况，对相同构件的曲率、残余位移角相加求和，并根据结构统一修复最严重的24个构件。其中，按曲率加权后统一修复的24个损伤严重的构件与按残余位移角加权后修复的24个损伤严重的构件相同，可将其表示为同一种。分析得到不同T况下结构在不同地震波下损伤指数与PGA的关系以及相应的结构地震易损性曲线分别如图11和图12所示。

由图11可以看出，震损结构在遭遇余震后的损伤程度远大于完好结构遭遇地震时的损伤程度，因此在地震后需要迅速采取合理的措施对震损结构进行修复或加固，提高结构的抗震能力，降低结构发生严重破坏甚至倒塌的风险。仅修复有限个损伤构件的震损结构在遭遇余地震后的损伤指数虽然得到降低，且不同修复方案的结果不同，但还是大于完好结构在主震下的损伤指数。在三种修复方案中，根据残余位移角对震损结构进行修复后，结构发生严重破坏以及倒塌的概率最小，修复后结构的抗震性能提高最显著。同时，由于实际震损结构的残余位移角恰好可以快速测量，因而宜将残余位移角作为首选表征损伤物理量进行震损评估。综上，在地震灾害后可根据实际震损结构中所有构件的残余位移角以及裂缝尺寸和数量对损伤程度进行量化，并根据量化结果和“择层修复”的策略去指导震损结构修复，从而能从最快速度和最大限度两方面提高结构的抗震能力，以保障人民的生命财产安全。gzslib202204041634

6 结 论

根据合理的损伤表征指标对震损结构中构件的损伤进行量化，并用于指导震损结构的快速修复加固，能够有效地提高震损结构抗震性能。本文针对目前真实震损结构中构件的损伤不易量化且修复后结构的抗震性能难以评估的现状，厘清了位移、曲率、残余位移以及损伤指数之间的关系，提出了在有限元软件中模拟损伤构件修复加固的方法和流程以及按不同物理量指标对构件损伤进行量化的方法。同时，在OpenSEES中分析了震损结构按不同的损伤物理量指标对构件进行快速修复后的抗震性能。主要结论如下：

（1）为克服真实震损结构可测信息有限、损伤难以量化的局限，在塑性铰理论的基础上，建立梁柱构件曲率与位移的关系，并进一步证明梁柱构件顶部位移和端部曲率之间具有明确线性关系、损伤指数与位移之间存在幂函数关系，为根据残余位移量化损伤程度提供途径。

（2）针对在有限元軟件中震损结构的修复加固难以模拟，修复后结构的抗震性能难以预估的问题，提出一种通过单元替换模拟震损结构中损伤构件进行修复的方法，并经过实例验证可知该方法具有合理性和准确性。

（3）建立了根据不同损伤物理量指标对震损结构中构件的损伤进行量化的方法，并通过分析震损结构按损伤表征指标进行快速修复后再历地震时的损伤程度可知，根据曲率和残余位移角对构件损伤进行量化并用于指导快速修复时，结构的损伤程度最低，抗震能力提升最明显。由于在震后检测中可快速准确地获取残余位移（角）数值，因此宜将其作为震损结构最关键的损伤表征指标。此外，震损结构的修复加固宜按照择层修复策略进行开展。

（4）由震损结构以及震损修复结构的地震易损性曲线可知，震损结构再历地震时有很大的风险出现严重破坏甚至倒塌的风险，而根据残余位移角对震损结构进行修复，能够有效提高结构的抗震能力，降低结构发生严重破坏和倒塌的风险。这证实了对震损结构进行修复加固具有十分重要的意义，为实际震损结构修复加固提供有力的理论支撑。

参考文献：

[1]李宏男，肖诗云，霍林生.汶川地震震害调查与启示[J].建筑结构学报，2008，29（4）：10-19.

LI Hongnan， XIAO Shiyun， HUO Linsheng. Damageinvestigation and analysis of engineering structures inthe Wenchuan earthquake[J].Journal of Building Struc-tures， 2008， 29（4）： 10-19.

[2] 张超，周云，翁大根，等.震损RC框架结构减震加固的可修性研究[J].土木工程学报，2014，47（S1）：207-213.

ZHANG Chao， ZHOU Yun， WENG Dagen， et al.Reparability of earthquakedamaged RC frame structurefor seismic retrofit with energy dissipation devices[Jl.Journal of Civil Engineering， 2014， 47（ S1）： 207-213.

[3]季静，乔升访，韩小雷，等.基于构件变形的RC框架结构可修复能力评估方法研究[J].建筑结构学报，2018，39（S1）：205211.

JI Jing，QIAO Shengfang，HAN Xia01ei，et al.RepairIability of RC frame using component performance basedmethod[J].Joumal of Building Structures，2018，39（S1）：205 211.

[4] Park Y，Ang A H.Mechanistic seismic damage modelfor reinforced concrete[J].Joumal of Structural Engi—neenng，1985，111（4）：722 739.

[5]杜修力，欧进萍.建筑结构地震破坏评估模型[J].世界地震工程，1991（3）：52 58.

DU Xiuli，OU Jinping.Earthquake damage evaluanonmodel of building structure[J].World Earthquake Engi—neering，1991（3）：52 58.

[6] 王东升，冯启民，王国新.考虑低周疲劳寿命的改进Park Ang地震损伤模型[J].土木丁程学报，2004，17（11）：41-49.

WANG Dongsheng，FENG Qimin，WANG Guoxin.A modified Park Ang seismic damage model considerIing low cvcle fatigue life[J].Joumal of Civil Engineer_ing，2004，17（11）：41 49.

[7] 周云，刘季.新型耗能（阻尼）减震器的开发与研究[J].地震工程与工程振动，1998，18（1）：71-79.

ZHOU Yun，LIU Ji Development and study of new en—ergy dissipaters（dampers）[J].Earthquake Engineeringand Engineering Vibration，1998，18（1）：71-79.

[8] 中华人民共和国住房和城乡建设部.地震灾后建筑鉴定与加固技术指南[M]，北京：中国建筑工业出版社，2008.gzslib202204041634

Ministry of Housing and Urban Rural Development ofthe People s Republic of China.Technical Guide forPost Earthquake SafetV Evaluation and Retrofit of Build—ings[M].Beijing：China Architecture Publishing&Me—dia Co.Ltd..2008.

[9]欧进萍，何政，吴斌，等.钢筋混凝土结构基于地震损伤性能的设计[J].地震工程与工程振动，1999（1）： 21-30.

OU Jinping，HE Zheng，WU Bin，et al.Seismic dam—age performance based design of reinforced concretestructures[J].Earthquake Engineering and EngineeringVibration，1999（1）：21-30.

[10]张宁.钢筋混凝土柱变形能力与水平位移计算研究[D].西安：长安大学，2018.

ZHANG Ning.Research on deformation ability and hor—izontal displacement calculation of reinforced concretecolumns[D].Xi‘an：Chan9 an University，2018.

[11]Priestley M，Park R.Strength and ductility of concretebridge columns under seismic loading[J].ACI Stmctural Joumal，1987，84（1）：61 76.

[12]Kunnath S K，Reinhom A M，Lobo R F.IDARC Version 3.0：A program for the inelastic damage analysis ofreinforced concrete structures[R].Technical ReportNCEER 92 0022，National Center for Earthquake En—gineering ResearCh， State University of New Y0rk，Buffalo，NY.USA.

[13]何浩祥，陈奎，范少勇.基于弹塑性耗能差率的地震损伤评估模型及分析方法[J].振动工程学报，2018，31（3）：382 390.HE Haoxiang， CHEN Kui， FAN Shaoyong. Seismicdamage model based on differential ratio of elastic plastic dissipated energy and application[Jl. Journal of Vibration Engineering， 2018， 31（3）：382-390.

[14]何浩祥，陈奎，王小兵.梁端填充低屈服点钢材的梁柱连接减震性能试验与损伤分析[J].建筑结构学报，2017. 38（5）：1-10.

HE Haoxiang， CHEN Kui. WAN（J Xiaobing. Experiment research and damage analysis on vibration absorption performance of filled steel connection[J].Joumal ofBuilding Structures. 2017， 38（5）：1-10.

[15] KRATZIG W B. MEYER I F. MESKOURIS K.Damage evolution in reinforced concrete members undercyclic loading[Cl. Proceedings of the 5th InternationalConference on Structural Safety and Reliability， SanFrancisco. 1989： 795802.

[16]何利，叶献国.Kratzig及ParkAng损伤指数模型比较研究[J].土木工程学报，2010，43（ 12）：1-6.

HE Li. YE Xianguo. Comparative of Kratzig and ParkAng damage index models[Jl. China Civil EngineeringJournal. 2010， 43（ 12）： 1-6.

[17]朱伯龙.结构抗震試验[M].北京：地震出版社，1989.ZHU Bolong. Structural Seismic Test[Ml. Beijing：Earthquake Press， 1989.

[18]日本道路協会.道路橘示方耆·同解说：V耐震设计编[S].束京：日本道路协会，2002.

Association of Highway of Japan. Design specificationsof highway bridges. Part V：seismic design[S].Tokyo：Association of Highway of Japan， 2002.

[19]崔济东.RC梁、柱及剪力墙变形性能指标限值研究与试验验证[D].广州：华南理工大学，2017.

CUI Jidong.Research and experimental verification ofdefOrmation index limits of RC beams. columns andshear wa11s[D].Guangzhou：South China University ofTechn0109y，2017.gzslib202204041634

[20]于曉辉.钢筋混凝土框架结构的概率地震易损性与风险分析[D].哈尔滨：哈尔滨工业大学，2012.

YU Xiaohui.Probabilistic seismic fragility and risk anal-ysis of reinforced concrete frame structures[D].Har_bin：Harbin Institute of Techn0109y，2012.

[21]Mitropoulou C C，Papadrakakis M.Devloping fragilitycurves based on neural network IDA prediction[J].Englneenng Structures，2011，33（12）：735 752.

[22]刘晶波，王文晖，赵冬冬，等.循环往复加载的地下结构Pushover分析方法及其在地震损伤分析中的应用[J].地震工程学报，2013，35（1）：21 28.

LIU Jingbo，WANG Wenhui，ZHA（）Dongd.ng，eta1.Pushover analysis method of underground structures under reversa1 1oad and its application in seismic damageanalysis[J].Journal of Earthquake Engineering，2013，35（1）：21 28.

[23]Gu X L，Shen Z Y.Damage analysis of reinfOrced concrete structures under earthquake series[C].Proceedings of The 7th International Conference on Computingin Civil and Building Engineering，Seoul，Korea，1997：1019-1024。

[24]何浩祥，陈奎，闫维明.基于小波包变换和时变频率的结构地震损伤评估[J].振动与冲击，2016，35（7）：23 30.