An Adaptive Nonhydrostatic Atmospheric Dynamical Core Using a Multi-Moment Constrained Finite Volume Method

Pei HUANG, Chungang CHEN*, Xingliang LI, Xueshun SHEN, and Feng XIAO

1State Key Laboratory for Strength and Vibration of Mechanical Structures,Xi’an Jiaotong University, Xi’an 710049, China

2Center of Numerical Weather Prediction, China Meteorological Administration, Beijing 100081, China

3Department of Mechanical Engineering, Tokyo Institute of Technology, Tokyo 226-8502, Japan

ABSTRACT An adaptive 2D nonhydrostatic dynamical core is proposed by using the multi-moment constrained finite-volume(MCV) scheme and the Berger-Oliger adaptive mesh refinement (AMR) algorithm. The MCV scheme takes several pointwise values within each computational cell as the predicted variables to build high-order schemes based on single-cell reconstruction. Two types of moments, such as the volume-integrated average (VIA) and point value (PV), are defined as constraint conditions to derive the updating formulations of the unknowns, and the constraint condition on VIA guarantees the rigorous conservation of the proposed model. In this study, the MCV scheme is implemented on a height-based, terrainfollowing grid with variable resolution to solve the nonhydrostatic governing equations of atmospheric dynamics. The AMR grid of Berger-Oliger consists of several groups of blocks with different resolutions, where the MCV model developed on a fixed structured mesh can be used directly. Numerical formulations are designed to implement the coarsefine interpolation and the flux correction for properly exchanging the solution information among different blocks. Widely used benchmark tests are carried out to evaluate the proposed model. The numerical experiments on uniform and AMR grids indicate that the adaptive model has promising potential for improving computational efficiency without losing accuracy.

Key words: adaptive mesh refinement, multi-moment constrained finite-volume method, nonhydrostatic model, dynamical core, high-order methods

1. Introduction

During the last few decades, increased attention has been paid toward improving numerical weather prediction(NWP) models for better resolving small-scale processes at high resolution. In terms of a dynamical core, much effort has been put forth to develop new numerical schemes and computational meshes with the intent of attaining higher accuracy and efficiency. Aside from the traditional methods, the high-order numerical schemes that are based on“local” or single-cell based spatial reconstruction are becoming more popular recently in developing the atmospheric dynamical cores because of their high-order accuracy, geometric flexibility, and their scalability on massive, parallel computer systems. The representative schemes are the spectral element method (Thomas and Loft, 2000; Iskandarani et al.,2002; Giraldo and Rosmond, 2004) and the discontinuous Galerkin method (Levy et al., 2007; Giraldo and Restelli,2008; Nair et al., 2009; Blaise and St-Cyr, 2012) among others.

The multi-moment constrained finite-volume (MCV)method (Ii and Xiao, 2009) was recently proposed as a new framework to develop high-order schemes. Several pointwise values at equidistantly distributed solution points are defined as predicted variables (unknowns) within each computational cell. The formulations for the spatial discretization of unknowns are derived through the constraint conditions provided by introducing different types of moments (Yabe and Aoki, 1991; Yabe et al., 2001; Ii et al., 2005; Xiao et al., 2006; Ii and Xiao, 2007; Chen and Xiao, 2008), such as point values, volume-integrated averages, derivatives of different orders, and so on. Using the MCV method, 2D and 3D nonhydrostatic dynamical cores have been proposed in Li et al. (2013) and Qin et al. (2019).

Though computational power has made rapid gains recently, atmospheric modeling is still highly time-consuming and computationally expensive work. Considering the multi-scale phenomena at operating in the atmosphere, the development of adaptive numerical models, which are capable of running on the computational meshes with variable spatial resolution, is a very effective way to save on computational costs. Some existing methods can conduct multi-resolution simulations in atmospheric modeling, such as the nested grid (Pielke et al., 1992), the stretched grid (Yessad and Bénard, 1996), and the AMR grid (Berger and Oliger, 1984;Behrens, 1996; Stevens and Bretherton, 1996; Tomlin et al.,1997; Kessler, 1999). Using an AMR grid is very attractive among these techniques for its flexibility and efficiency in dynamic adjusting a computational mesh according to the time-evolution of predicted variables. AMR techniques have been applied in some atmospheric models to improve the computational efficiency, examples include the studies described in Skamarock et al. (1989), Skamarock and Klemp (1993), Blayo and Debreu (1999), Bacon et al.(2000), Hubbard and Nikiforakis (2003), Jablonowski et al.(2006), St-Cyr et al. (2008), and Chen et al. (2011). In this study, we will develop an adaptive MCV nonhydrostatic model with the applications of Berger and Oliger’s AMR algorithm based on the 2D model proposed in Li et al.(2013).

The remainder of this paper is organized as follows. A 2D nonhydrostatic dynamical core using a 3-point MCV scheme is briefly described in section 2. The setup and dynamic adjustment of an AMR mesh, along with numerical operations to exchange the solution information among different blocks under the framework of the MCV scheme,are described in section 3. Numerical results of the widely used benchmark tests are given in section 4, and a short summary is given in section 5.

2. The two-dimensional (2D) compressible nonhydrostatic MCV dynamical core

A 2D compressible nonhydrostatic atmospheric dynamical core was proposed in Li et al. (2013) using a multimoment constrained finite volume method. We implement this MCV dynamical core on the AMR grid in this study.The governing equations for the compressible nonhydrostatic dynamical core are written in conservative flux-form as

where the dependent variables are the density (ρ), the momentum vector (ρu,ρw), and the product of density and potential temperature ρ θ; p is pressure and g is the acceleration of gravity. The effects of rotation are not considered in this implementation.

To deal with bottom topography, the height-based, terrain-following coordinates (x,ζ) proposed in Schär et al.(2002) are adopted. The Jacobians of the transformation are. In computational space, the uniform grid ( x,ζ) is related to the Cartesian coordinate as

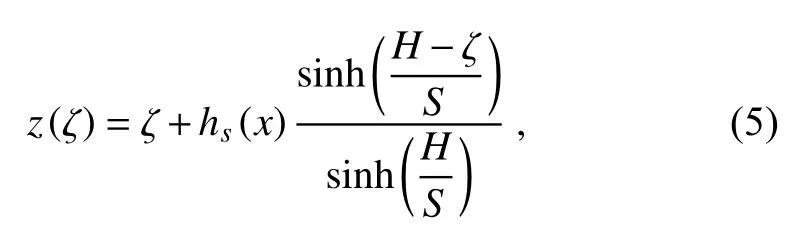
where hsis the height of the bottom of the mountain, H is the model top, and the parameter S = 3000 m is adopted.is the contravariant vertical velocity component in the transformed coordinate defined as

where u and w are velocity components for the Cartesian coordinate system (x,z)

Splitting of the hydrostatic reference state is usually applied in atmospheric modeling to improve accuracy. As a result, the thermodynamical variables are written as

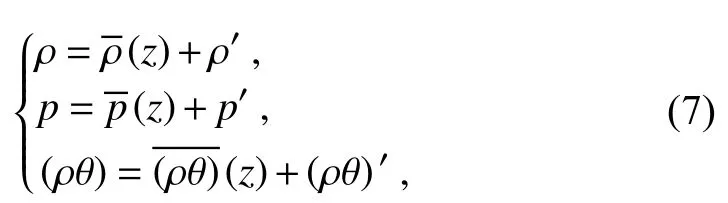
where ρ′, p′and (ρθ)′are the deviations of the thermodynamical variables, the reference state satisfies the hydrostatic relation

A 3-point MCV scheme of third-order accuracy (Ii and Xiao, 2009) is adopted to solve the governing equations,Eqs. (1)-(4) in this study. Hereafter, we briefly describe the MCV formulations by considering the 1D hyperbolic conservation law having the form of

where q is the vector of dependent variables and f is the vector of flux function.

Within each cell, three local degrees of freedom(DOFs), in terms of point-wise values qi,m(m = 1 to 3), are defined at two endpointsand the center xias shown in Fig. 1a for the cell Ci.

Fig. 1. Distribution of DOFs for the (a) 1D case and (b) 2D Cartesian grid.

With known values of local DOFs, a quadratic Lagrangian polynomial Qi(x) can be constructed as

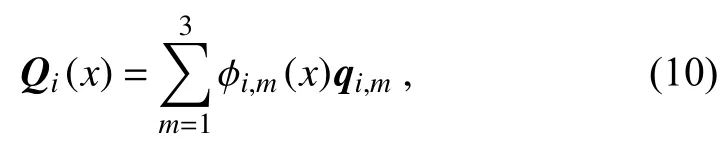
where the Lagrangian basis function is

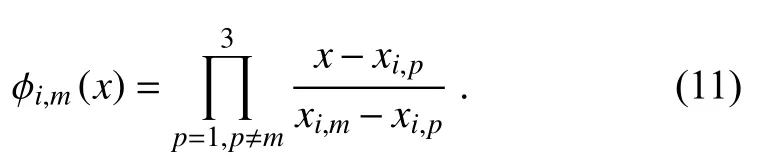
To build the MCV scheme, two kinds of moments including the PV (point value) momentat cell interface and the VIA (volume-integrated average) momentover each cell are defined to derive the spatial discretization formulations (Ii and Xiao, 2009). At the cell interface, the PV moment (same as the DOF defined at the cell’s endpoint) is updated using the differential-form governing equations through solving the derivative Riemann problem. The VIA moment is updated using flux-form finite volume formulations and assures the rigorous numerical conservation. The updating formulations for the DOF defined at the cell center are then derived through a constraint condition on the VIA moment. The details of the numerical procedure to derive the updating formulations for the 3-point MCV scheme can be referred to Ii and Xiao (2009). For the sake of brevity, we directly give the semi-discrete formulations for three different DOFs as

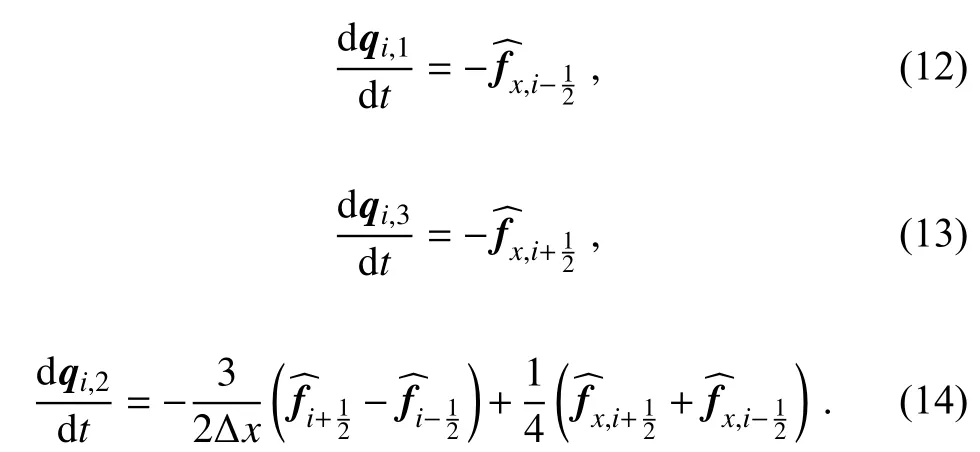
where a is the maximum absolute value of the eigenvalues of the Jacobian matrix ∂ f/∂q. The derivatives of dependent variables and flux functions are evaluated using the Lagrangian interpolation polynomials having the form of Eq.(10), and the subscripts L and R denote the cells Ciand Ci+1.

As shown in Ii and Xiao (2009), the 3-point MCV scheme shown above is of 3rd-order accuracy and preserves the rigorous numerical conservation in terms of the VIA moment given by

The MCV scheme can be easily extended to the multidimensional models by applying the above one-dimensional formulations in different directions one-by-one (Ii and Xiao, 2009). As shown in Fig. 1b, nine local DOFs in terms of point-wise values are defined within the cell Ci,jto build the two-dimensional numerical models using the 3-point MCV scheme. Similarly, the numerical conservation is assured by the VIA moment, which is determined by the two-dimensional Simpson’s rule as

where the indices i and j are omitted on the right-hand side of Eq. (17) for the sake of brevity.

For time-stepping, a third-order Runge-Kutta scheme is adopted to update the following semi-discrete ordinary differential equation (ODE) obtained from the above spatial discretization:

The solution is advanced from q(n)at time t(n)to q(n+1)at time t(n+1)by

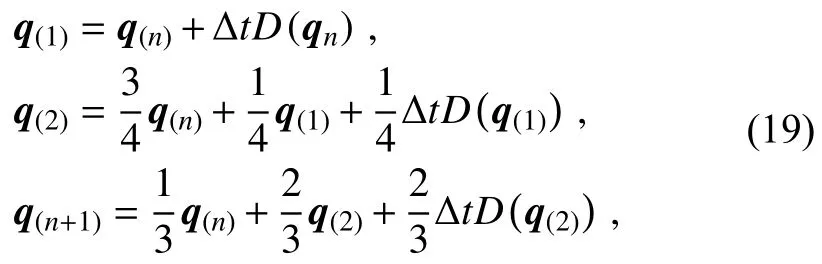
with Δt=t(n+1)-t(n)as the time step. The time integration strategy for the AMR grids will be demonstrated in later contents.

The details of the numerical formulations for a twodimensional MCV nonhydrostatic dynamical core are described in Li et al. (2013).

3. Adaptive mesh refinement algorithm

The AMR algorithm proposed by Berger and Oliger(1984) uses a set of blocks to cover the whole computational domain. On each block, the structured computational mesh is constructed to implement the spatial discretization.These blocks are grouped into different levels according to their spatial resolutions and the blocks with finer resolution always overlay the blocks belonging to the next coarser levels. The governing equations can be solved on each block independently if enough ghost cells, which are either copied from the adjacent blocks of the same level or evaluated by coarse-fine interpolations from blocks of the next coarser level, are supplemented. Additionally, the AMR algorithm also implements the dynamic adjustment of blocks according to the time evolution of the predicted fields. Since the high-order discretization is implemented using the single-cell based stencils in MCV models, the coarse-fine interpolations are easily accomplished and extra numerical errors due to the non-uniform resolution can be more effectively suppressed in comparison with existing variable-resolution models, as shown in our previous study(Chen et al., 2011). The operations to generate and adjust the AMR grid along with some additional numerical procedures to implement the MCV model on an AMR grid are briefly introduced in this section. Without losing generality,here, we consider the uniform Cartesian grid (x,y) on each block, i.e., the grid spacing is hk=Δxk=Δykon level k.

3.1. Grid generation and dynamic adjustment

In the beginning, a base block (level 0) is first built,which covers the whole computational domain and has the coarsest resolution. Then, finer levels are generated one by one following a similar procedure. Given the kth-level blocks, the next finer level is generated as follows.

3.1.1. Flagging the cells to be refined

All cells belonging to level k are checked by some refinement criterion to find those cells where the physical fields should be solved using finer resolution to improve the accuracy. Berger and Oliver (1984) introduced a criterion based on the error estimation using Richardson extrapolation.Though it is a general methodology for different types of applications, a more efficient criterion is to check the known flow structures of some representative physical variable in atmospheric modeling. In this study, we flag the cell to be refined if the variation of some indicative variable across the cell is larger than a prescribed threshold.

3.1.2. Generating the blocks of level k+1

The simplest way is to use just one block, which is the smallest rectangle (in 2D computational space) is to cover all flagged cells. However, it is inefficient since, in general,the domain consisting of the flagged cells is highly irregular, and using a single structured block will result in many un-flagged cells being involved at the finer level k+1. To improve the efficiency, we divide one big block into two small ones and it is expected that the area of each small one then can be reduced to cover the flagged cells. The division of an existing block will be conducted continuously until the ratio between the area covered by un-flagged cells and the total area on this block is smaller than a prescribed value. In this study, we adopted a division method based on pattern recognition (Berger and Rigoutsos, 1991) instead of a simple bisection to speed up this operation.

The above procedure is repeated until the finest level has been constructed. During the simulations, the computational meshes are completely or partially adjusted every several time steps to track the evolution of predicted fields.This adjustment starts from the fine level and most of the above operations can be applied with some modifications.When the grid adjustment is finished, values of predicted variables in the newly generated fine cells are interpolated from the coarser level. Coarse-fine interpolation operations based on a single-cell stencil are described later in this section.

3.2. Time marching and flux correction on an adaptive grid

In this study, a time marching step is chosen to keep the same CFL (Courant-Friedrichs-Lewy) number on different levels. In two-dimensional case, the CFL number on level k is. Considering that the refinement ratio of grid resolution is an integer, λ , between levels kand k +1, the corresponding grid spacings and time steps on these two adjacent levels are hk=λhk+1and Δtk=λΔtk+1. With variable time steps on different levels, the governing equations are advanced for λ steps on level k+1 during one step on level k. In Fig. 2, the time marching procedure from tnto tn+1=tn+Δt is illustrated for a 3-level AMR grid. Each level is advanced through Eq. (19) with its own time integration interval. For the sake of simplicity, the refinement ratio is chosen as λ =2 hereafter in all illustrative examples. A special recursive procedure is adopted for time marching on an AMR grid, i.e., any coarse level cannot be advanced to the next time step until all finer levels have reached the current time instant. Additionally, the coarse-fine interpolations are conducted both in time and space to evaluate the ghost cells.In this study, the temporal interpolation is accomplished by a linear reconstruction of the predicted fields at two adjacent time steps.

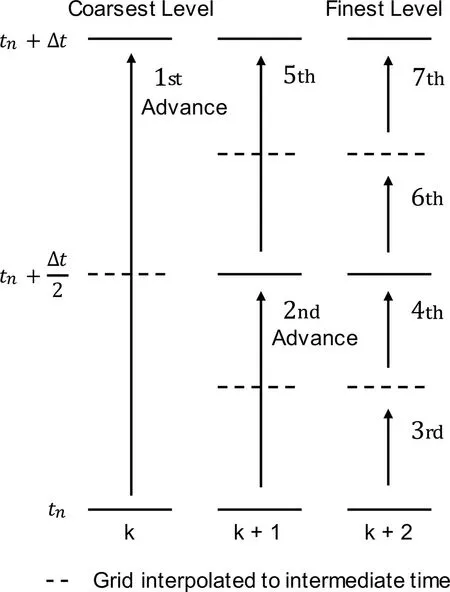
Fig. 2. Diagram depicting the subcycling of AMR levels in time.

To guarantee the numerical conservation, flux correction should be conducted along the interfaces between the coarse and fine levels (Berger, 1989, 1998). As shown in Fig. 3, Fi+1,j,krepresents the time-averaged numerical flux during one time step on level k, and is used to update,the VIA moment of the coarse cell Ci,j,k. During the same time interval, VIA moments of the adjacent fine cells C2i+1,2j,k+1and C2i+1,2j-1,k+1are advanced by time-averaged numerical fluxes f2i+1,2j,k+1and f2i+1,2j-1,k+1. Since the relation Fi+1,j,k=(f2i+1,2j-1,k+1+f2i+1,2j,k+1)/2 is not assured by the raw scheme, the AMR model is not conservative without a flux correction operation.

In the proposed model, the VIA moment of a coarse cell is corrected to assure the numerical conservation by:

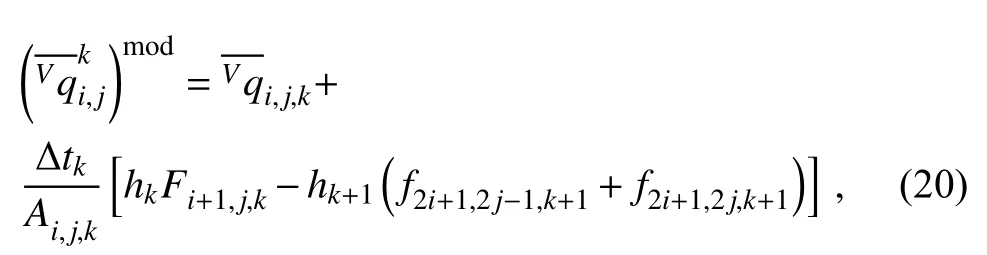
where Ai,j,kis the area of the coarse cell, Ci,j,k.

3.3. Cross-level interpolation

The solution transfer between coarse and fine levels plays an important role to accomplish the numerical modeling on an AMR grid. In the proposed model, numerical solutions on level k are only exchanged with the two adjacent levels, k -1 and k +1.

Since the numerical solutions with finer resolution are of higher accuracy, they are used to replace the solutions in the overlap regions on the next coarser level through a fineto-coarse solution transfer. As shown in Fig. 4, at the solution points defined along the edges of the coarse cell(denoted by solid circles), the values of predicted variables are directly copied from the corresponding solution points(denoted by hollow circles) on the finer level. At the center of the coarse cell, the point-wise values (denoted by solid triangles) are evaluated to preserve the numerical conservation, i.e., it is calculated through Eq. (17) with the VIA obtained through the relation

Fig. 3. Flux correction along the interface between the coarse and fine levels.

Fig. 4. Fine-to-coarse solution transfer in the overlap regions.

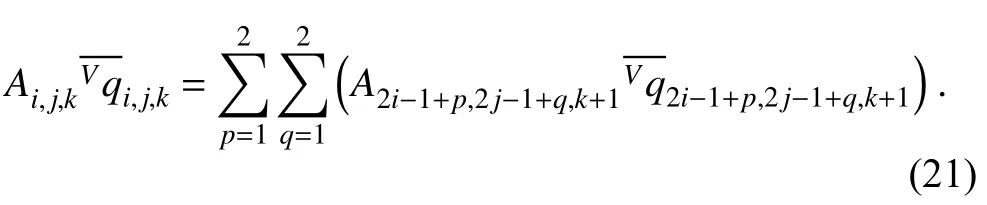
The coarse-to-fine solution transfer is adopted to supplement the ghost cells and to evaluate the solutions within the newly generated fine cells.

In Fig. 5, the coarse-to-fine solution transfer to supplement the ghost cells is illustrated. A coarse cell Ci,j,kis adjacent to the fine cells C2i+1,2j,k+1and C2i+1,2j-1,k+1on level k+1. Fine cells C2i,2j,k+1and C2i,2j-1,k+1are ghost cells,where the solutions should be interpolated from the coarse cell Ci,j,kto provide the boundary conditions. Ghost points denoted by solid circles coincide with solution points within Ci,j,k, and the values of predicted variables can be directly copied from the known solutions. Ghost points, denoted by solid squares, are not solution points of level k, and values of physical fields have to be evaluated through single-cell(Ci,j,k) based Lagrangian interpolation polynomials, which are 2D quadratic polynomials. For some variable, Q, these take the form of

where the coefficients are decided by nine constraint conditions provided by known DOFs.

The coarse-fine interpolations to evaluate predicted variables in newly generated fine cells are more complicated, as the rigorous numerical conservation should be preserved.As shown in Fig. 6, the coarse cell Ci,j,kis divided into four fine cells C2i-1,2j-1,k+1, C2i-1,2j,k+1, C2i,2j-1,k+1, and C2i,2j,k+1.The predicted variables should be evaluated at all solution points on level k+1 (denoted by solid shapes). At solution points denoted by solid circles and squares, the same algorithm is adopted either by copy or interpolation, as mentioned above, to set up the fine ghost cells. However, at internal points denoted by solid triangles, the point-wise values should be determined to preserve the numerical conservation. First, the VIAs of some variable q within four fine cells are evaluated by

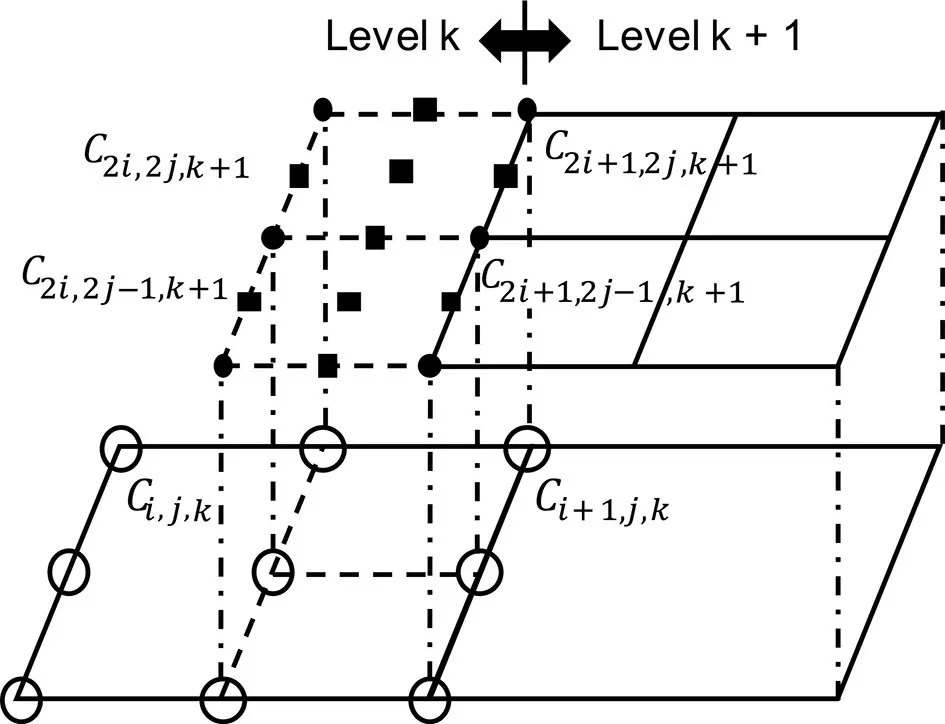
Fig. 5. Coarse-fine interpolations based on multi-moments for evaluating the ghost cells.

Fig. 6. Coarse-fine interpolations based on multi-moments for evaluating the flow variables in newly generated fine cells.

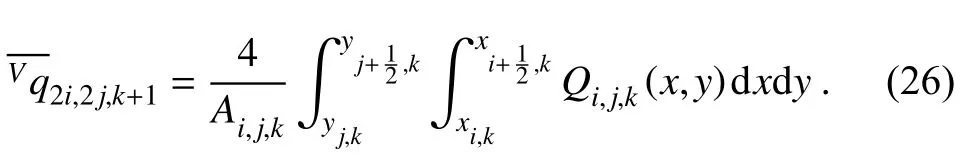
Then the point-wise value at the cell center denoted by the solid triangle is obtained through the two-dimensional Simpson’s rule [see Eq. (17)] in each newly generated fine cell.

4. Numerical tests and results

To check the performance of the adaptive model in improving the computational efficiency, the widely used benchmark test cases are carried out in this section. The performance of the MCV dynamical core on a fixed grid has been validated in Li et al. (2013) and the numerical results are comparable to those of existing advanced models. In this study, we run the MCV dynamical core on adaptive grids with different configurations. The adaptive grid is denoted by N×M×l×λ. N and M represent the number of cells along the horizontal and vertical directions respectively, which means the base block (the coarsest level) consists of N×M computational cells, the finest level is level l and the refinement ratio between two adjacent levels is λ. It is noted that the minimum grid spacing is allowed by the finest level l. The normalized l1, l2and l∞errors (Williamson et al., 1992) and computational costs are examined. Definitions of the normalized errors are given as follows:

where Ω is the computational domain,andare the numerical and reference solutions in terms of cell-integrated averages. All numerical tests in this study are carried out on the AMD EYPC 7702 CPU (single processor).

The initial hydrostatic state is specified as

where the Exner pressure is given by . The constants are cp=1004.5Jkg-1K-1and Rd=287Jkg-1K-1.

The basic state of potential temperature, θ, is chosen to be a constant

or specified with a constant Brunt-Väisälä frequency as

The refinement criterion is chosen as the variation of the potential temperature perturbation for the rising thermal bubble, density current flow, and internal gravity waves, as well the variation of horizontal velocity for the Schär mountain case. Considering a two-dimensional cell Ci,j,kon level k, it is flagged to be refined if

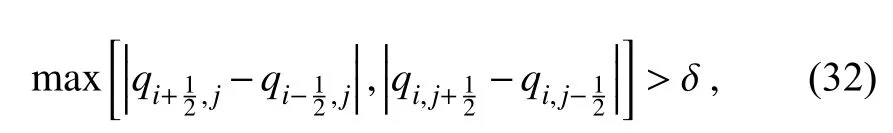
where δ is a prescribed threshold, and q can be the potential temperature perturbation, θ′, or the horizontal velocity, u.

4.1. A rising convective thermal bubble

Atmospheric motions caused by thermodynamic effects(Carpenter et al., 1990; Wicker and Skamarock, 1998;Ahmad and Lindeman, 2007; Norman et al., 2011) are common phenomena in nature. They are extensively used to verify the performance of dynamical cores. In this test, a thermal bubble that is warmer than the ambient air is initialized by specifying a positive potential temperature perturbation as

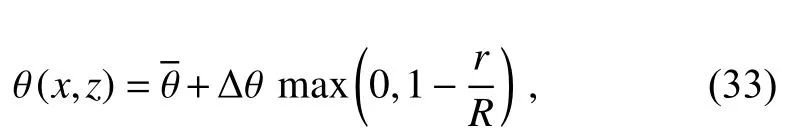
In this case, the uniform background potential temperature is specified as=300K, the maximal perturbation is Δθ=2K and the computational domain is [0, 20] km × [0,10] km. The simulation runs for 1000 s and all boundaries are slippery walls. The explicit dissipation filter (Li et al.,2013) with a viscosity coefficient, μ=10m2s-1, is used to eliminate numerical noise. The threshold for refinement is set as δ=0.04. During the simulation, the thermal bubble rises and finally attains a mushroom-like shape. The numerical results on a uniform grid, with a resolution of 25 m ×25 m, are used as a reference solution to calculate the normalized errors.

Normalized errors and elapsed CPU time for different grids are given in Table 1, where the results are grouped according to the finest resolution on an adaptive grid. The normalized CPU time is also computed by dividing the CPU time on the coarsest uniform grid. From Table 1, it can be found that the normalized errors of the numerical results on the uniform and AMR grids within each group are quite similar, noting that much less CPU time is consumed by the AMR model. Contour plots of the potential temperature perturbation (θ′) and the absolute errors on a 100×50×3×2 grid at different times are shown in Fig. 7. The solid thick lines represent the interfaces between different levels. The symmetric distribution of θ′is perfectly reproduced on the adaptive grid as in our previous studies (Li et al., 2013). It is observed that the fine levels are dynamically adjusted to fit the change of flow field. AMR grids properly locate the disturbed region and put the fine blocks there to assure numerical accuracy. In undisturbed regions, the coarse blocks are applied to save computational costs. The relative total mass error along the simulation is also recorded, which supports that the numerical conservation property is well achieved through the flux correction procedure.

4.2. Density current

In the density current test case (Straka et al., 1993; Giraldo and Restelli, 2008), a cold bubble is put in a neutrally stratified atmosphere by specifying a negative potential temperature perturbation as

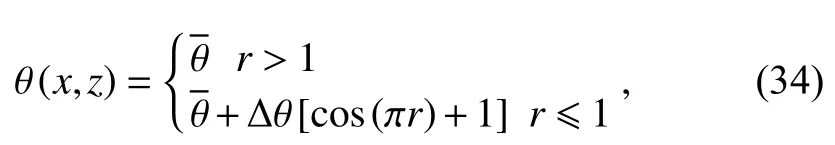
where

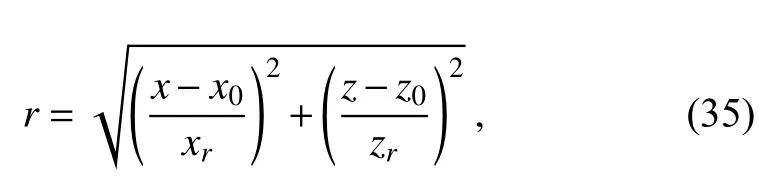
During the simulation, the cold bubble drops to the ground and spreads out in the horizontal direction to form three Kelvin-Helmholtz shear instability rotors along the cold frontal surface. The computational domain of this case is [-26.5, 26.5] km × [0, 6.4] km and the simulation time is 900 s. All of the boundaries are slippery walls. A dissipation filter with a coefficient of μ =10m2s-1is used to meet the requirement of a physical process. The threshold of the refinement criterion of this case is δ =0.2. Again, the numerical results on a uniform grid with a resolution of 25 m ×25 m are adopted as reference solutions.

Normalized errors of θ′and elapsed CPU time on different grids are given in Table 2. It can be observed that the AMR model consumes much less computational costs at the price of slightly larger normalized errors. Contour plots of θ′and the absolute errors on a 132×32×2×4 grid are shown in Fig. 8, which have the finest resolution of 50 m ×50 m. Only half of the computational domain is depicted due to the symmetry of the flow field. The numerical result agrees well with those on the uniform grid with the same resolution given in Li et al., (2013).

4.3. Internal gravity waves

The internal gravity waves test involves the evolution of a potential temperature perturbation in a channel with periodic boundary conditions in the horizontal direction. Initial conditions used in Skamarock and Klemp (1994) are adopted. The potential temperature field is initialized as

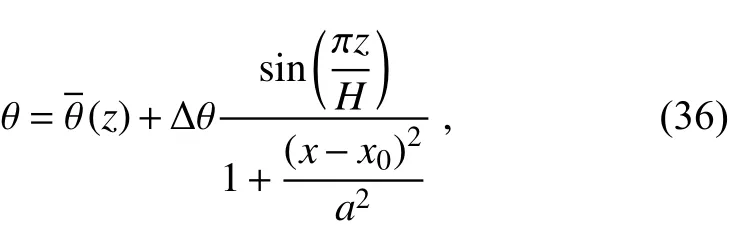
where θ0=300K,H=10km, Δθ=0.01K,x0=100km,anda=5km.

The background state of potential temperature(z) is obtained by using a constant Brunt-Väisälä frequency. A constant mean flow of=20ms-1for the advection of the internal gravity waves is adopted. The bottom and top boundaries are slippery walls. The computational domain of this case is [0, 300] km × [0, 10] km, and the simulation time is 3000 s. δ =1.8×10-4is chosen for grid refinement. Numerical results on a 250 m × 25 m grid are taken as the reference solutions. It is noted that the computational cells are no longer square, an aspect ratio of grid spacing Δx=10Δzis adopted in this case.

Normalized errors of θ′and elapsed CPU times on various grids are given in Table 3. Comparing to the first two test cases, the effect of AMR grids in saving computational costs is less obvious. The reason is that the internal gravity waves are spreading in the horizontal direction during the simulation and the disturbed regions are continuously growing as shown in Fig. 9. Maximum and minimum values of ver-tical velocity and potential temperature perturbation on the AMR grids with the finest resolution of Δz=100mafter 3000 s are given in Table 4, which is the same as that obtained by Li et al (2013). The distribution of the absoluteerrors of θ′on a uniform grid and a 75 × 25 × 3 × 2 grid att=3000s is depicted in Figs. 10a, b. No obvious increase of errors is found around the boundaries between different levels, which reveals that the computational mode due tothe change of grid resolution is effectively suppressed in the proposed AMR model. The general errors in the AMR model are also affected by the prescribed refinement threshold. More accurate solutions are obtained when a larger area of the computational domain is refined with a smaller refinement threshold.

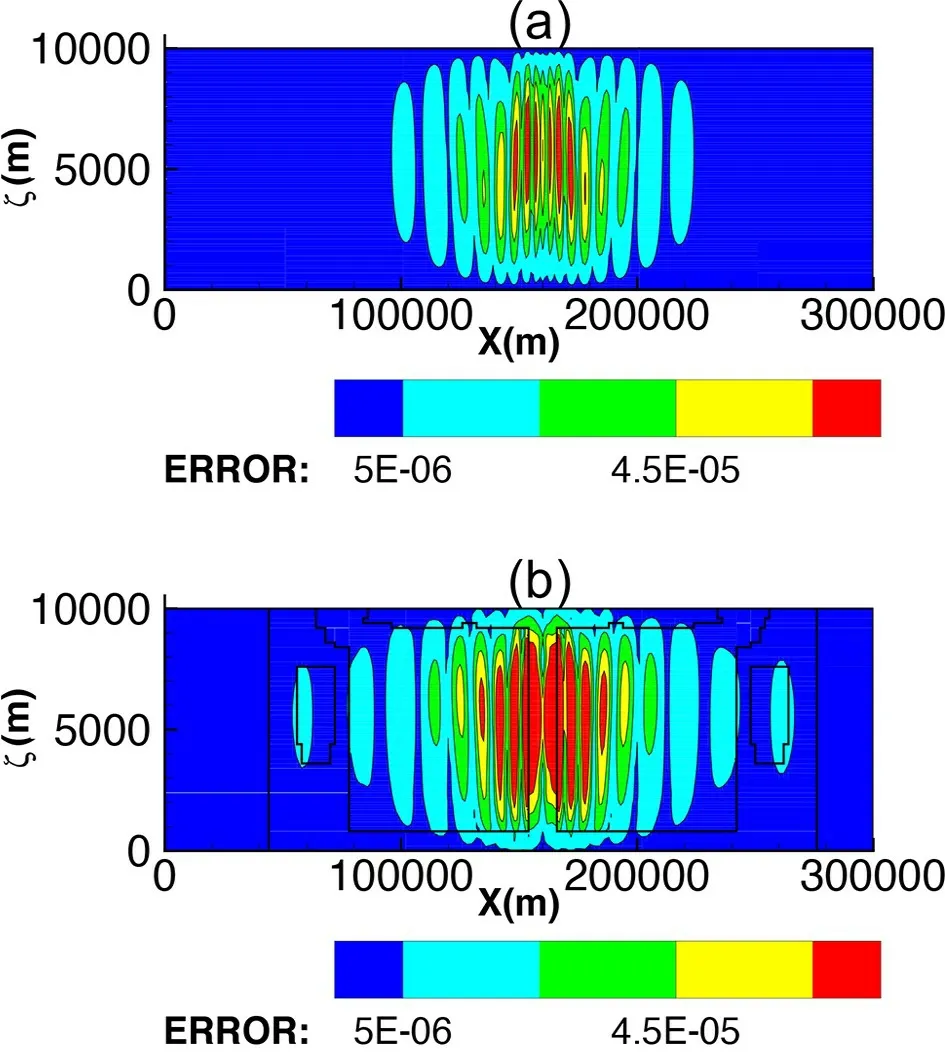
Fig. 10. Error distribution of the potential temperature perturbation (θ′) for the internal gravity waves on the (a)uniform grid and (b) 7 5×25×3×2 grid at t = 3000 s.

Table 4. Maximum and minimum of vertical velocity, w, and potential temperature perturbation, θ′ , for the internal gravity waves test on the AMR grids with the finest resolution, Δ z=100m after 3000 s.

Fig. 9. Contour plots of potential temperature perturbation (θ′ ) for the internal gravity waves on 7 5×25×3×2 grid at(a) t = 0 s, (b) t = 750 s, (c) t =1500 s, (d) t = 2250 s, and (e) t = 3000 s.

Table 3. Normalized errors of potential temperature perturbation (θ′) and elapsed CPU time for internal gravity waves test running on different grids.

Fig. 8. Contour plots of the potential temperature perturbation (θ′) and its errors for the density current on 132×32×2×4 grid at (a) t = 0 s, (b) t = 225 s, (c) t = 450 s, (d) t = 675 s, (e) t = 900 s, and (f) absolute errors.

Table 2. Normalized errors of the potential temperature perturbation (θ′) and elapsed CPU time for the density current test running on different grids.

Fig. 7. Contour plots of a potential temperature perturbation (θ′) and its errors for a rising thermal bubble on 100×50×3×2 grid at (a) t = 0 s, (b) t = 250 s, (c) t = 500 s, (d) t = 750 s, (e) t = 1000 s, and (f) absolute errors.

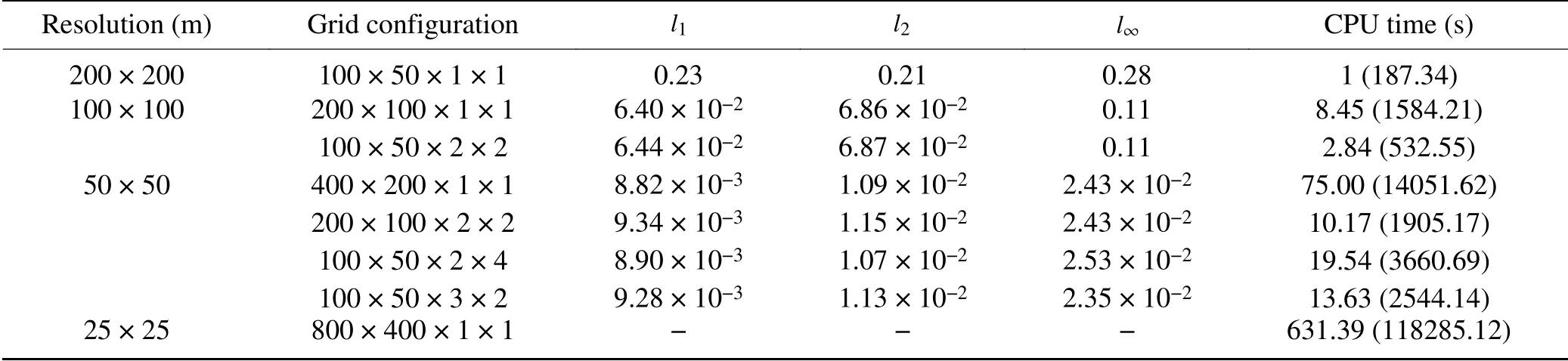
Table 1. Normalized errors of the potential temperature perturbation (θ′) and elapsed CPU time for the thermal bubble test running on different grids.

4.4. Schär mountain

The Schär mountain case (Schär et al., 2002) is used to test the ability of a model to deal with the effects of complex terrain. A mountain with five peaks is used as topography which is specifically defined as

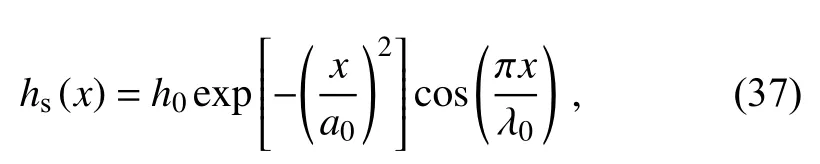
where h0=250m, a0=5000m, and λ0=4000m. An initial background state of potential temperature is obtained by using a constant Brunt-Väisälä frequency of N0=10-2s-1and θ0=280K. A constant mean flow of u=10ms-1along the horizontal is also initialized. This case is running on a domain of [-25, 25] km × [0, 21] km for 10 hours. Nonreflecting boundary conditions are implemented by putting sponge layers in the area of z≥9 km for the top boundary and |x|≥15 km for the lateral inflow and outflow boundaries. The bottom boundary is a slippery wall. A refinement threshold, δ =0.3, is applied to this case.

The profile of the Schär mountain is depicted in Fig. 11e,noting that only part of the computational domain is displayed. Contour plots of the horizontal velocity, u, at various stages in the simulations are displayed in Figs. 11a-d.Since the disturbed regions quickly extended to cover the entire computational domain, it is not expected that the computational costs can be significantly saved by AMR models.Numerical results on a uniform fine grid with a resolution of 125 m × 105 m are used as reference solutions and the corresponding normalized errors are given in Table 5. The elapsed CPU time of the AMR model is about 44% of that on the uniform grid. The AMR grid does not affect accuracy since the numerical errors after 10 hours are almost the same as those on the uniform grid with the same resolution.

Table 5. Normalized errors of horizontal velocity (u) and elapsed CPU time for the Schär mountain test running on different grids.

Fig. 11. Contour plots of horizontal velocity ( u ) of the Schär mountain case at (a) t = 7200 s, (b) t = 16800 s, (c) t =26400 s, (d) t = 36000 s, and (e) the shape and size of the Schär mountain.

5. Conclusion

In this paper, an adaptive nonhydrostatic atmospheric dynamical core is proposed by using the multi-moment constrained, finite-volume method and Berger-Oliger’s adaptive mesh refinement algorithm. The high-order scheme is constructed based on two kinds of local degrees of freedom. As a result, the spatial reconstruction for a 3rd-order scheme is accomplished based on a single-cell-based stencil. The compact spatial stencil is beneficial for the efficient implementation of coarse-fine interpolation and reduction of the extra numerical errors due to the non-uniform resolution of an AMR grid. The proposed model runs on the adaptive grid consisting of blocks with different resolutions. The blocks with fine resolutions are placed in those regions that contain large variations of physical fields in order to improve the numerical accuracy, while the blocks with coarse resolutions are placed in the remainder of the area to save computational costs. With the evolution of flow fields, the distributions of blocks are dynamically adjusted to guarantee that the regions with complex flow structures are always resolved with fine resolutions. Numerical results of widely used benchmark tests reveal the effectiveness of the AMR technique in saving computational costs. It is observed that the use of an adaptive grid has only a very slight negative impact on computational accuracy in comparison with results on fixed grids with the same resolution.

Today, finer predictions of small-scale weather and climate phenomena and their interactions with large-scale ones gain more and more attention. Though the supercomputing capacity has been greatly increased recently, the use of an AMR grid would be beneficial in reducing unnecessary computational cells and make it more affordable to accurately track spatially complex and time-dependent small-scale phenomena. However, using an AMR grid has the undesirable side-effect of making it more difficult to achieve high scalability, since it is not easy to keep satisfying load balance among different CPUs on time-varying computational meshes. It is a major challenge to construct a practical atmospheric model using adaptive mesh.

Promising results by the proposed adaptive model have shown great potential in applying the proposed numerical framework to develop a more efficient atmospheric dynamical core. Future research will mainly focus on the extension of an adaptive model to the three-dimensional regional and global dynamical cores.

Acknowledgements.This work is supported by The National Key Research and Development Program of China(Grants Nos. 2017YFA0603901 and 2017YFC1501901) and The National Natural Science Foundation of China (Grant No.41522504).