ABAQUS软件在淠史杭灌区水闸闸室稳定计算中的应用

陆 璐

（安徽省淠史杭灌区管理总局设计院 合肥 230088）

1 引言

在淠史杭灌区水闸一类建筑物的常规设计过程中，需要根据《水闸设计规范》（SL265-2016）中结构计算章节内关于水闸闸室稳定的计算公式对水闸进行相关验算复核，其中计算内容除了包括水闸闸室的抗滑稳定性还需要验证闸室在抗倾覆稳定方面以及水闸进出口两侧的翼墙的结构稳定是否满足要求。经过多年的运用实践，灌区内水闸的设计多采用1 孔或多孔作为结构型式，纵向不设分缝。常规规范公式法在计算闸室稳定时通常忽略闸室各个组成部分之间的互相作用，将水闸闸室看作成一个单元，即作为一个整体进行计算，这种计算方式简单直接，并且为设计工作提供了便利。

2 工程概况

戚家桥泄水闸位于安徽省六安市戚家桥集附近的淠河总干渠左岸11+000 处，主要作用是排除总干渠右岸山丘区44.40km2面积的来水，并可将总干渠水放空，以便渠道进行维修。戚家桥泄水闸是淠史杭灌区安全畅通运行的关键性控制工程之一，是保证灌区正常灌溉和城市供水的重要措施，对改善农业生产条件，提高水资源利用率，促进六安市城南镇社会经济可持续发展，对于灌区发展和城市发展都具有重大意义。

2013年戚家桥泄水闸进行拆除重建。新建的戚家桥泄水闸采用潜孔式水闸型式，共3 孔，单孔净宽5.0m，总净宽15.0m。水闸底槛高程为47.33m，检修平台顶高程53.93m，闸室顺水流方向长12.0m，边墩厚1.0m，中墩厚1.2m，闸室总宽度为19.4m。启闭机台顶面高程为59.73m，启闭机房净高3.5m，净宽5.0m。闸室主要部位均为C25 钢筋混凝土结构。考虑到与现状闸顶交通桥两岸道路的顺畅连接，闸上交通桥布置在闸室上游侧，与水闸墩墙整体浇筑。水闸结构形式采用三孔一联的整体箱涵式基础，闸室上部荷载可均匀传递到至水闸地基上，从而减小不均匀沉降。

3 计算模型及参数

3.1 计算模型

将整个闸室以及上部建筑作为本次计算的整体研究对象，利用ABAQUS 软件建立三维有限元模型，模型结构包含闸室底板、闸墩、检修便桥、交通桥、工作闸门、启闭机房、桥头堡和地基础。根据工程场地地质条件，地基土体服从莫尔-库仑屈服准则，符合弹塑性材料判定标准。结合广义胡克定律，用线弹性材料构建莫尔-库仑模型，从而详尽展示水闸闸室混凝土材料的本构关系。本次计算模型是根据笛卡尔直角坐标系进行分解，分为X、Y、Z 三个方向。其中X 方向指的是顺着水流方向指向下游，Y 方向指的是垂直水流方向指向上游，Z 方向指的是纵轴指向上。

考虑到在三维空间里建立模型，有限元分析计算结果与结构基础选取尺寸标准有很大影响，本次计算模型选取基础的尺寸范围扩大至水闸上下游及左右两侧相应尺寸的一倍大小，基础选取深度设定为21m。同时，在有限元模型中向基础底部施加受力，侧面施加水平法向链杆受力，从而尽可能使模型的规格符合实际情况，提高计算结果的准确性。有限元模型采用C3D8R 六面体约简线性积分单元进行结构网格划分，将闸室分解成16314 个节点，共10922 个单元格，将地基分解成10032 个节点，共8262 个单元格，尽可能准确地反映出水闸闸室和基础之间的位移变化情况，计算模型见图1。

图1 计算模型图

3.2 初始地应力的平衡

根据工程区地质条件，地基土体因承受自身重力，存在初始应力。垂直沉降位移的数值正常控制在10～14 个数量级，基本可以忽略不计，符合地基应力平衡。

3.3 材料的物理力学参数

模型选取线弹性材料模拟闸室混凝土，选取弹塑性材料模拟闸室基础土体，见表1。

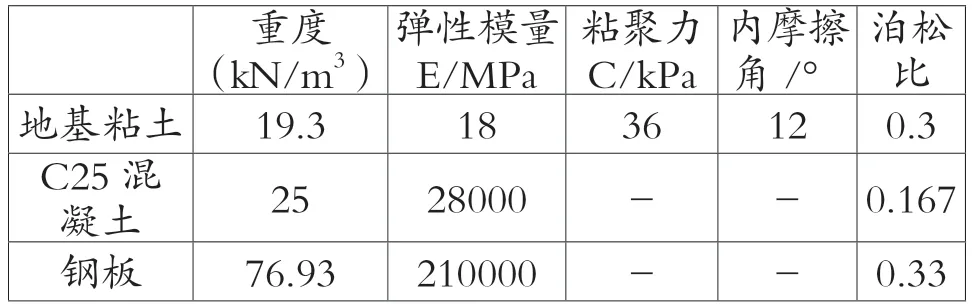
表1 材料物理力学参数取值表

3.4 在不同工况下闸室稳定成果分析

闸室的稳定性分析主要是建模后通过闸室的平均基础应力是否超过各种计算条件下地基的容许承载力来判别。行业规范中要求在各种计算条件下，闸室基础的最大应力与最小应力之比不得大于规范允许值，同时闸室的最大基底应力不应超过标准地基容许承载力的1.2 倍。本次关于水闸闸室结构建立的有限元模型用来分析闸室底板在不同条件下承载的竖向应力，分析成果显示闸室稳定情况满足规范要求。

3.4.1 完建期工况下的闸室稳定成果分析

在完建期，采用ABAQUS 有限元软件对模型进行计算，计算结果中的水闸基底应力分布情况，见图2。

图2 完建期闸室基底应力分布图和应力等值线图

由分布图可知，完建期水闸的基底应力在设计水位工况下均为受压，闸室基底最大压应力为75kPa，最小压应力50kPa。其中，在闸门以及闸墩的位置出现了应力集中分布的现象，其中最大压应力分布在边墩的上下游外边缘处，压应力值为0.3MPa，其他部位应力分布比较均匀。由此可见，水闸的闸底板承受力来自上部结构的自重以及不均匀剪力。经计算，闸室基底最大压应力与最小压应力的比值为1.5，因此，完建期水闸闸室稳定计算结果满足规范要求。

3.4.2 设计洪水位工况下闸室稳定成果分析

在设计洪水位工况下，采用ABAQUS 有限元软件对模型进行计算，计算结果中的水闸基底应力分布情况见图3。

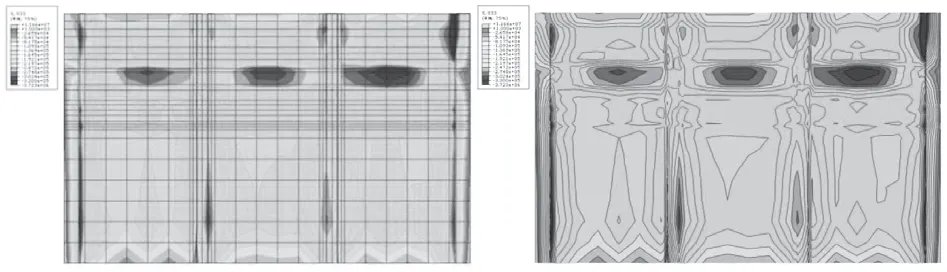
图3 设计洪水位下闸室基底应力分布图和应力等值线图

由图3可知，完建期水闸的基底应力在设计水位工况下均为受压，闸室基底最大压应力为81.7kPa，最小压应力54.2kPa。其中，在闸门以及闸墩的位置出现了应力集中分布的现象，其中最大压应力分布在边墩的上下游外边缘处，压应力值为0.37MPa，其他部位应力分布比较均匀。由此可见，水闸的闸底板承受力来自上部结构的自重以及不均匀剪力。经计算，闸室基底最大压应力与最小压应力的比值为1.51，因此，完建期水闸闸室稳定计算结果满足规范要求。

3.4.3 校核洪水位工况下闸室稳定成果分析

在校核洪水位工况下，采用ABAQUS 有限元软件对模型进行计算，计算结果中的水闸基底应力分布情况见图4。

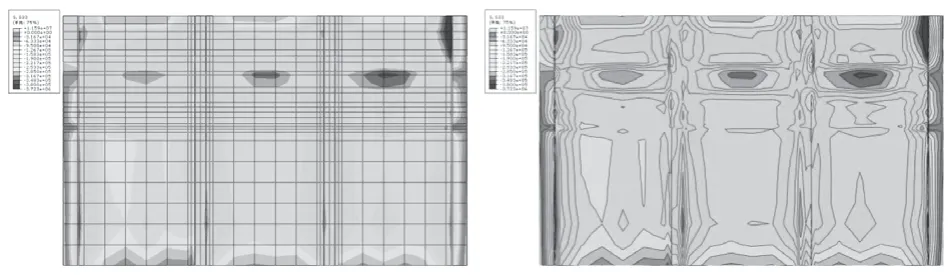
图4 校核洪水位下闸室基底应力分布图和应力等值线图

由图4可知，水闸的基底应力在校核水位工况下均为受压，闸室基底最大压应力为95kPa，最小压应力63.3kPa。其中，在闸门以及闸墩的位置出现了应力集中分布的现象，其中最大压应力分布在边墩的上下游外边缘处，压应力值为0.348MPa，其他部位应力分布比较均匀。由此可见，水闸的闸底板承受力来自上部结构的自重以及不均匀剪力。经计算，闸室基底最大压应力与最小压应力的比值为1.50，因此，校核洪水位工况下水闸闸室稳定计算结果满足规范要求。

3.4.4 正常蓄水位加地震工况下闸室稳定成果分析

在正常蓄水位加地震工况下，采用ABAQUS 有限元软件对模型进行计算，计算结果中的水闸基底应力分布情况见图5。

图5 正常蓄水位加地震工况闸室基底应力分布图和应力等值线图

由图5可知，水闸的基底应力在正常蓄水位加地震工况下均为受压，闸室基底最大压应力为87.5kPa，最小压应力58.3kPa。其中，在闸门以及闸墩的位置出现了应力集中分布的现象，其中最大压应力分布在边墩的上下游外边缘处，压应力值为0.32MPa，其他部位应力分布比较均匀。由此可见，水闸的闸底板承受力来自上部结构的自重以及不均匀剪力。经计算，闸室基底最大压应力与最小压应力的比值为1.50，因此，校核洪水位工况下水闸闸室稳定计算结果满足规范要求。

4 规范公式法与ABAQUS 软件计算结果的对比

为了便于分析两种计算方法的结果，对四种工况下闸室稳定计算结果进行了总结。经过基于ABAQUS 软件进行的有限元分析法和与常规规范公式法的计算结果进行对比复核，两种计算方法得到的结果都满足水闸《水闸设计规范》（SL265-2001）规范要求。具体结果见表2。

表2 两种方法计算结果对比表

5 结语

从计算结果看出有限元法得出的计算比值稍大一些，并且闸室底板出现了局部的应力集中现象，因为对水闸模型在进行网格划分时，网格节点会发生几何形状变形。但是从上述计算数值可以看出，规范公式法的计算结果与采用ABAQUS 软件进行有限元分析法的计算结果差别不大，两种计算方法的计算结果均满足规范要求。

水闸设计规范中的公式计算法具有普遍适用性，但相比较而言，有限元分析法能够将水闸闸室的基底应力的变化情况更为详尽地展现出来，且能够真实反映闸室结构的受力状况，具有更高的精确性和准确性，可以为淠史杭灌区内水闸设计工作提供更精准的技术支撑■