基于传输矩阵理论的Bragg 光栅特性研究

伊浩天

(南开大学物理科学学院，天津 300071)

0 引言

布拉格（Bragg）光栅是一种特殊的光栅结构，折射率周期性变化，在布拉格波长处，光栅的周期是光在该介质中的平均波长的一半，布拉格波长具有最大反射率，且在该波长的谐波处也可以产生较大的反射。Bragg 光栅可以作为光学滤波器或布拉格反射器，在光纤传感、光纤激光器、半导体激光器中均有广泛的应用[1]。

对于Bragg 光栅而言，常用的分析方法有耦合模理论（Couple-Wave Theory,CWT）[2][6]和传输矩阵理论（Transfer Matrix Method,TMM）[3][6]。CWT 是分析微扰下光在波导中传播行为的通用方法，在Bragg光栅内，正反向传播的光在折射率调制的作用下发生模式耦合。能够诠释波导中前向模、后向模，导波模、包层模、辐射模等模式间的能量交换。TMM 是结合数值算法，用一定数量的离散单元矩阵来描述整个光栅。应用这一模型时，把光栅分为很多小部分，并假设在每个部分中的光场是沿光栅均匀分布的，把左右边界处前向波和后向波之间的关系用一个2×2 的矩阵表示，称为传输矩阵。整个光栅的传输矩阵由每个小部分的传输矩阵相乘得到。相比于CWT，TMM 的主要优点有：

(1)TMM 只需建立全程的传输矩阵，而不必去解模式耦合方程，运算量大大减少；

(2) 相同的矩阵模块对于各种Bragg 光栅都可适用，不论是光栅Bragg 光栅，还是波导Bragg 光栅[4]。

1 传输矩阵理论

1.1 双层介质系统的传输矩阵模型

对于双层介质系统，给出电磁场的边值关系如下：

式中σ和α是面自由电荷和电流的密度，在绝缘介质界面上，σ=0，α=0。由于以上四式并非相互独立，(3)(4)式可以由(1)(2)式导出，因此，界面上的电磁场边值关系只需考虑以下两式：

以TE 波为例，研究电磁波在二维双层介质(界面垂直于z 轴)中传播时，入射波、反射波和折射波的振幅变化。双层介质的界面处的TE 波的传播示意图如图1 所示。

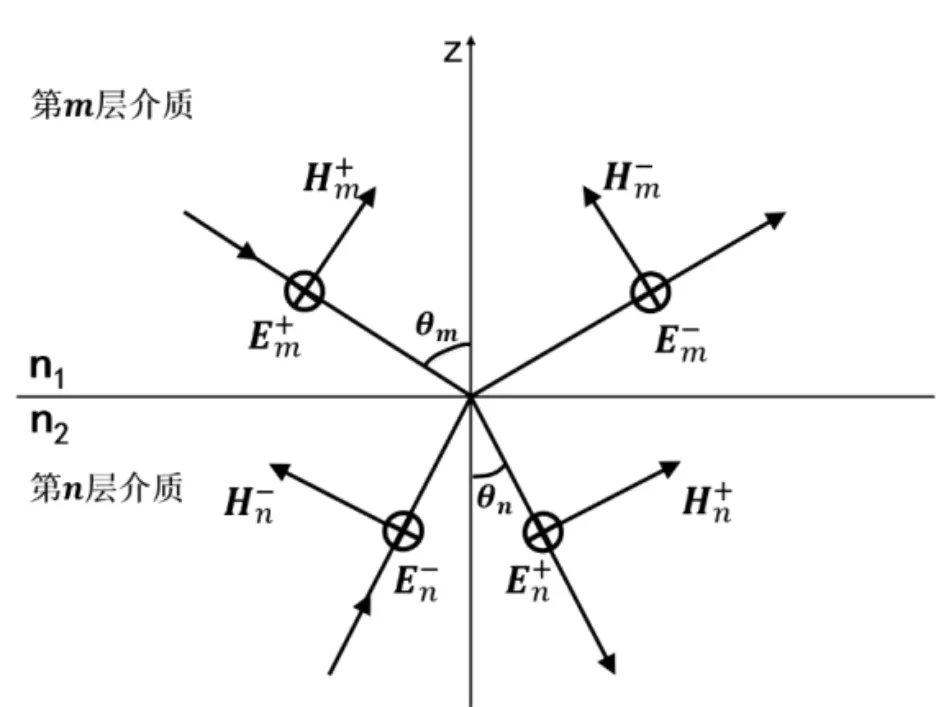
图1 界面处的电磁波(TE 波)

当界面上自由电流密度α=0时，根据边值关系有：

将(9)式代入(8)式可化简得：

由(7)式和(10)式可得如下关系：

对(11)式两边矩阵同时求逆，则可写为如下形式：

其中αnm为TE波从第m层介质传到第n层介质时的界面矩阵，其形式为：

期刊共被引分析可以帮助我们找出比较关注名物化研究的国内外核心刊物。国内数据分析显示，名物化研究引文来源期刊按中心度排名前10的依次是：《中国语文》《外语教学与研究》《现代外语》《外语研究》《外语与外语教学》《外语教学》《外国语》《北京大学学报》《外语学刊》《西安外国语大学学报》等。

当TE波以一定角度θm在折射率为n1,厚度为d的介质体内传播时，正向波和反向波的相位变化为±km nmdcosθm。

其中βn为TE波在第n层介质传播时的传播矩阵，其形式为：

这里,km=n12π/λ，λ为波长，n1为介质折射率。对于正入射的情况，Em=θn=0，此时(13)和(15)化简为：

根据菲涅尔公式可知，TE波从介质m到介质n的透射系数tmn和反射系数rmn为：

由此可得TE波从介质m到介质n的透射率T和反射率R：

1.2 Bragg 光栅的传输矩阵模型

如图2 所示，Bragg 光栅是指介质的折射率呈周期性变化的一种器件结构，能够对特定的波长实现选择作用。光波在Bragg 光栅中传播时在每个折射率跳变的界面发生反射，当波长满足布拉格条件时，从不同分界面反射的光相位相同，从而发生干涉加强，进而形成强反射峰，这种现象称为布拉格反射。产生布拉格反射的条件为：

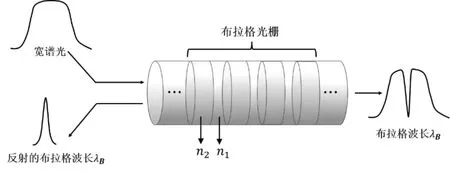
图2 Bragg 光栅结构示意图

根据图3 中所示，对于一个周期的Bragg 光栅，可将其分为A1、A2、A3、A4四个部分，每个部分可以用一个2×2 矩阵进行表示[1][6]：

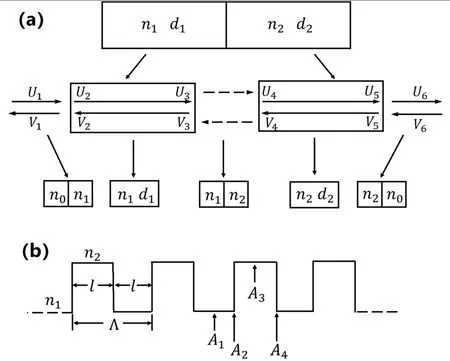
图3 （a）传输矩阵法示意图（b）Bragg 光栅折射率分布图

对于仅由两种不同折射率介质构成的周期性单元结构(包含两个折射率突变结构：n1→n2，n2→n1和两个长度均为d的匀质波导单元)，其传输矩阵可由以下四个矩阵单元相乘表示：

由上述分析可知，当研究多层膜结构中电磁波传播时。可以先建立一套矩阵理论来描述此过程。当一列平面电磁波垂直入射到多层膜结构时，会在不同材料的界面处经历反射和透射，而这些反射和透射的波各自又会在经历他们自己的反射与透射过程，因此在每一个固定的区域内都会存在很多反射波和透射波。为简化起见，我们将所有向前传播的光波归称为一个前向波Ui，将所有向后传播的光波归称为一个后向波Vi，这样我们可以用界面矩阵[5](图3 中A2和A4)和传播矩阵(图3 中A1和A3)来描述波在界面和介质中传播的过程，此时复杂的光栅结构即可化简为两种单独的单元结构，而光栅总的传输矩阵可由每个单元矩阵相乘得到。

式中n=L/Λ，Bragg 光栅总反射率与透射率可表示为：

2 Bragg 光栅的特性仿真

根据公式(23a)～(23d)和(24)可知，Bragg 光栅的反射谱和透射谱特性主要受光栅长度、光栅周期和光栅折射率三个因素的影响。下面分别对三个参数对反射谱和透射谱的影响进行分析。

2.1 Bragg 光栅长度对反射谱和透射谱的影响

假设Bragg 光栅的周期为Λ=535nm，折射率n1=1.461，n2=1.455，改变光栅的长度，用MATLAB对光栅反射谱和透射谱进行仿真，如图4～图6 所示。

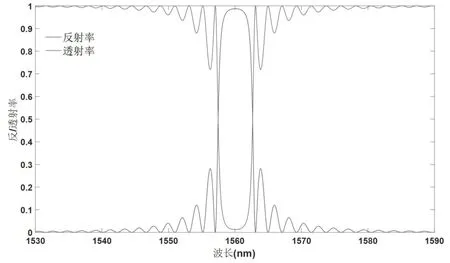
图4 Bragg 光栅周期数为700 时的反射谱与透射谱曲线

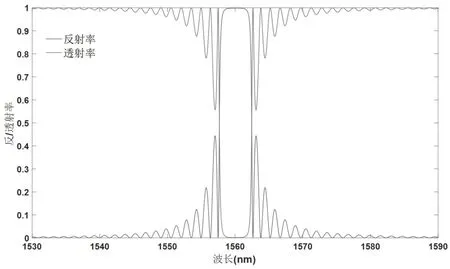
图5 Bragg 光栅周期数为1000 时的反射谱与透射谱曲线

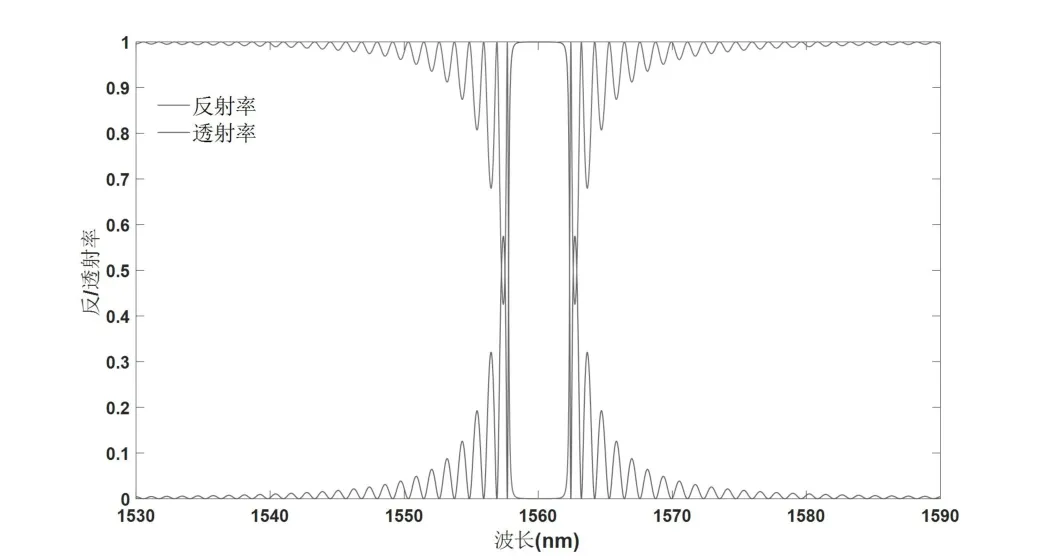
图6 Bragg 光栅周期数为1300 时的反射谱与透射谱曲线

光栅周期设为为Λ=535nm，折射率n1=1.461，n2=1.455时，根据布拉格条件可知布拉格波长λB=1560nm。从图4～图6 可以看出，随着光栅周期数的增多即光栅长度的增加，布拉格波长λB并没有发生变化，但布拉格波长处的反射率逐渐增大，透射率逐渐减小，且反射谱和透射谱逐渐变宽。这是因为当光栅长度增加时，从原来较短长度的光栅透射的光会被后续的光栅继续反射，从而导致反射率升高，透射率下降。根据布拉格条件，在其他参数不变的情况下，光栅长度的增加并不会影响主极大峰的位置，但会使布拉格波长附近的反射率逼近于1，这同样体现了Bragg 光栅对特定波长筛选功能的增强。

2.2 Bragg 光栅周期对反射谱和透射谱的影响

将Bragg 光栅周期数设置为1000，折射率n1=1.461，n2=1.455不变，改变光栅周期的大小，用MATLAB 对光栅反射谱和透射谱进行仿真，如图7 和图8 所示。

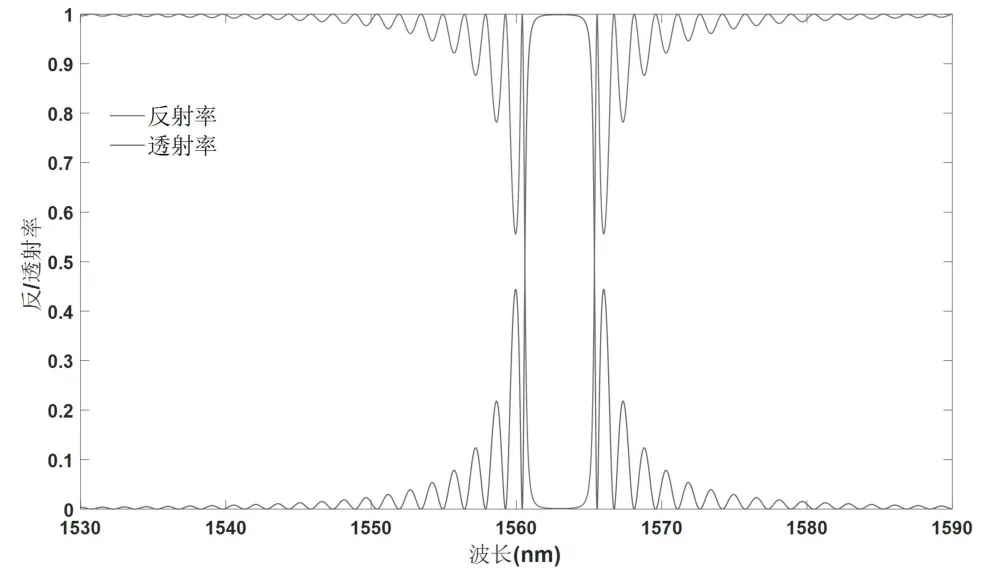
图7 Bragg 光栅周期为536nm 时的反射谱与透射谱特性

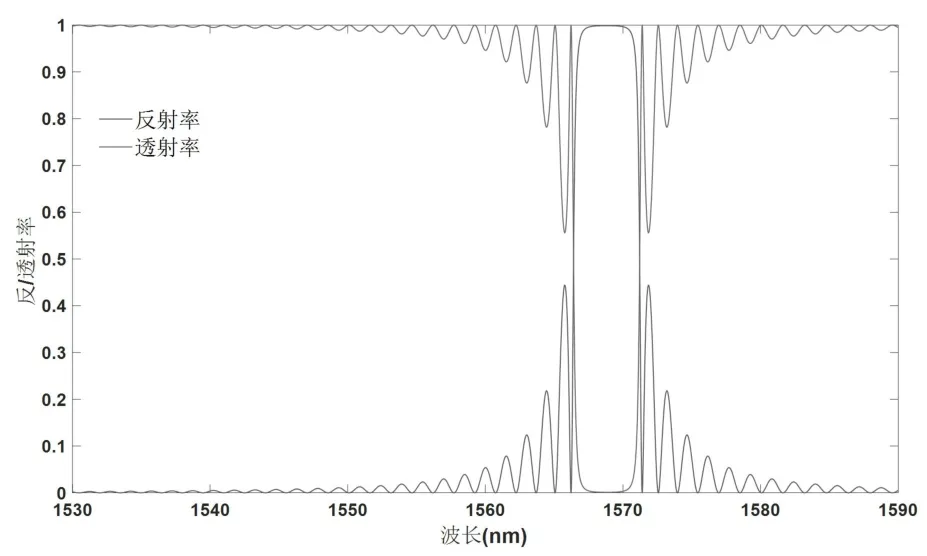
图8 Bragg 光栅周期为538nm 时的反射谱与透射谱特性

通过对比图5、图7 和图8 的变化可以看出，在其他参数不变的条件下，增大光栅周期时，主极大峰出现明显的右移，即布拉格波长变长。这是由于布拉格条件的限制，当有效折射率neff不变时，布拉格波长λB随光栅周期Λ 的增大而增大，但整体峰形及宽度并未发生明显改变。

2.3 Bragg 光栅折射率对反射谱和透射谱的影响

保持Bragg 光栅周期数1000 和光栅周期Λ=535nm不变，逐渐增加折射率n1，用MATLAB 对光栅反射谱和透射谱进行仿真，如图9 和图10 所示。

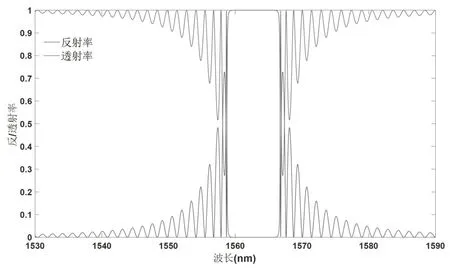
图9 Bragg 光栅n1=1.466 时的反射谱与透射谱特性

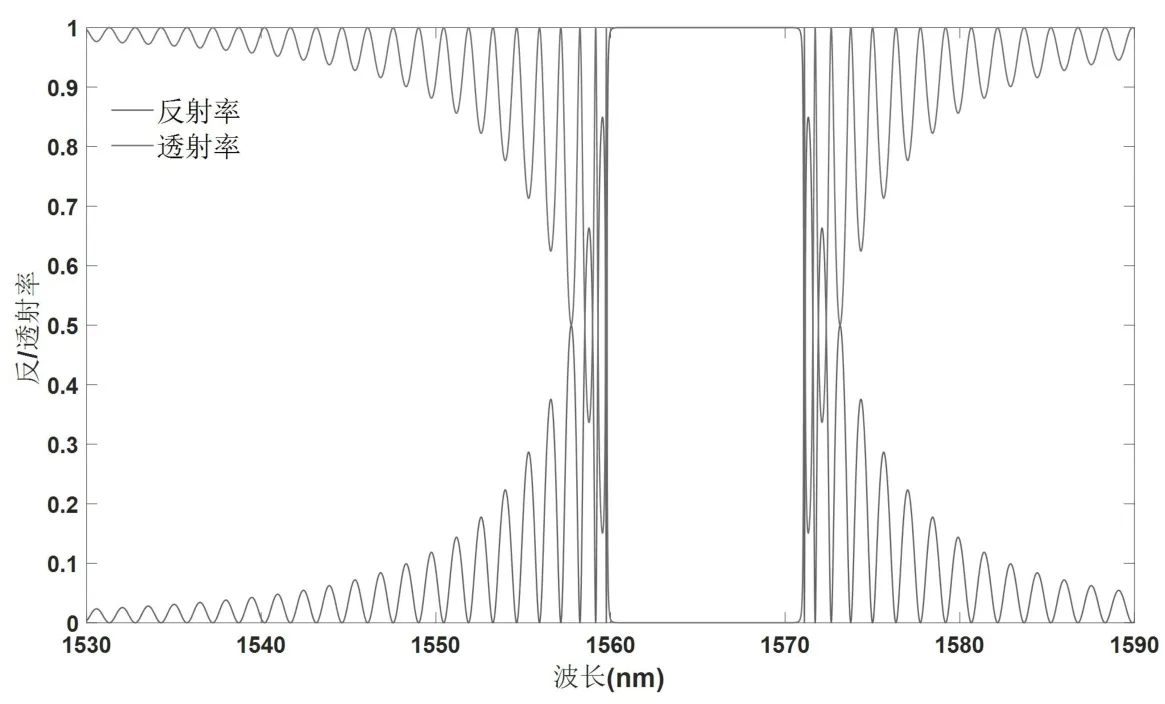
图10 Bragg 光栅n1=1.471 时的反射谱与透射谱特性

由于Bragg 光栅中相邻介质的折射率相差不大，且相邻介质层的厚度相同，因此有效折射率neff可以表示为：

对比图5、图7 和图8 可以看出，在其他参数不变的情况下，随着n1的增大，主极大峰的位置发生明显右移即布拉格波长变长；同时反射谱的宽度也明显增大，致使布拉格波长附近的反射率变大，透射率变小。根据式(22)可知，在光栅周期不变的情况下，增大有效折射率neff会使布拉格波长变大，主峰位置右移。

3 结论

本文从双介质系统入手，根据电磁场在介质表面的边值关系推导出光波在双介质系统中传播所满足的菲涅尔公式，从而过渡到简洁的矩阵表达形式。基于此，进一步建立了用于分析光纤Bragg 光栅的传输矩阵模型，通过把每一块折射率不同的介质抽象为一个2×2 的矩阵，将这些离散单元矩阵依次相乘即可用来描述整个光栅，这样入射端和出射端处的前向波和后向波之间的关系即可用该矩阵进行描述，大大简化了原本繁杂的计算过程。利用传输矩阵模型，通过MATLAB 编程实现了传输矩阵的数学算法，并以图像的形式展现了Bragg 光栅的反射谱与透射谱特性。通过对光栅长度、光栅周期、光栅折射率等参数对反射谱和透射谱的影响进行分析，直观的展现了各个参数在光栅中所起到的作用。