探寻引力常数测量值与地球的自转速率相配合的原因
方杰
(广州天行建筑设计院,广东 广州 510308)
0 引言
一般的物理学研究中,取一定的参考系用以度量有关的物理量,然后经过实验总结出其中的规律,发现基本方程。在这个过程中时空的几何性质不受有关的物理过程影响。所以,这些问题中的基本方程是物理量之间的一些关系,即:一些物理量=另一些物理量。在引力问题中,引力一方面要影响各种物体的运动,另一方面又要影响各局部惯性系之间的关系。因此,在引力基本方程式中应有时空的几何量。它应反映出,引力本身及引力与其他物质之间的作用,即有下列形式的方程:
1 正文
P0计算式见式(4),P0的计算值见表1,地球赤道上空空间曲率K0的计算值见表2。通过表1、表2中的数值比较,可以看出,χ=1,结合上述理论,发现K0是地球引力场的其中一个“时空的几何量”,他等于引力动量P0的值。
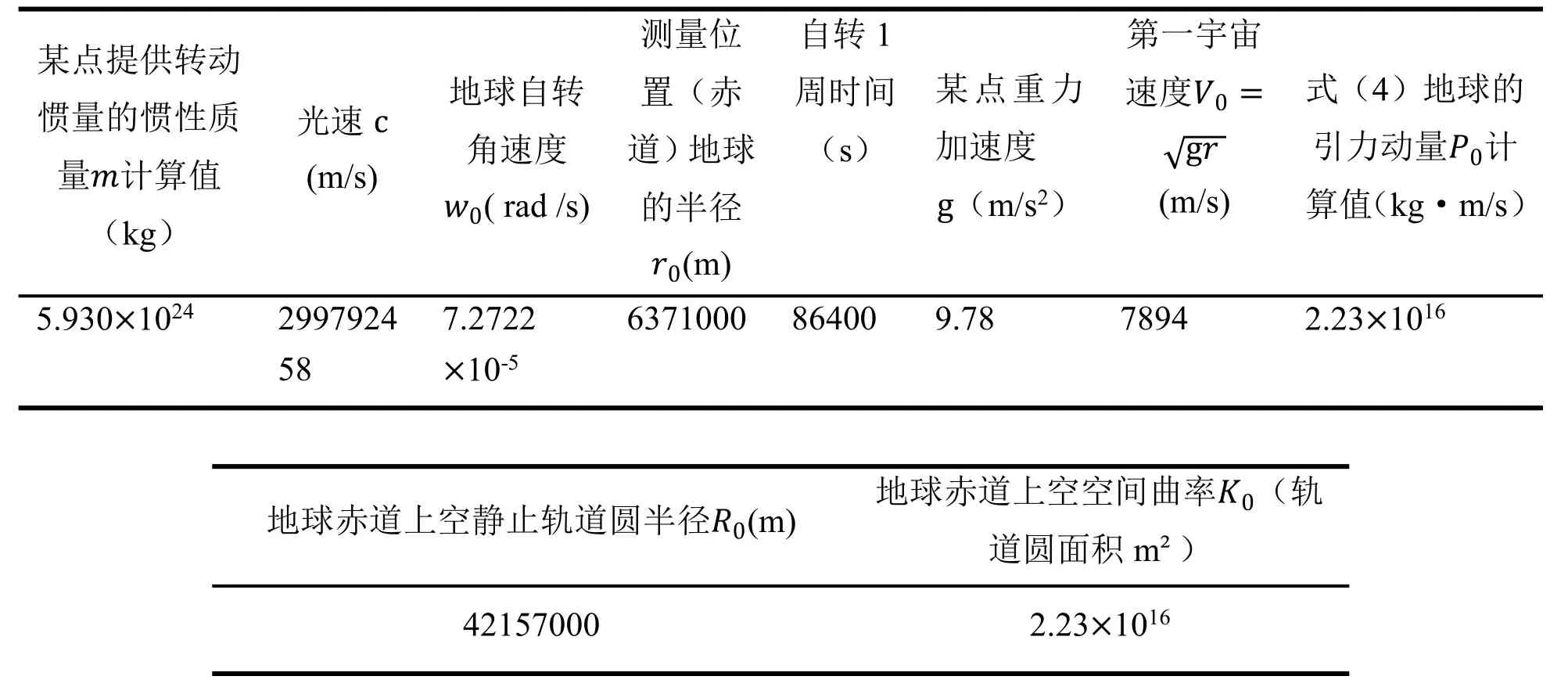
表1 地球引力动量P0计算值。
地球的转动惯量与地球的质量有关,同时与质量的分布情况有关。[4]地球惯性质量分布不均匀,地球表面不同地点与地球引力场中心点连线的惯性质量与地球地质内核情况有关,现在还没有准确数据或无法探测,对于地球表面不同地点提供转动惯量的惯性质量m这个变量,通过其外在表现的参数(地球表面不同地点的重力加速度)来体现,通过转动动能、引力动量、开普勒第三定律两者发生联系,计算方法见式(7)及表3。
物体(或人造卫星)在地球轨道R0上运行(R=R0),物体的角速度同步于地球的自转角速度ω0,此时物体的轨道是圆形轨道,结合开普勒第三定律及牛顿引力定律,此轨道R0有:
(T为公转周期,此时物体与地球为相同角速度,等于自转周期;d为引力场中某点与场中心点的距离;w0为地球自转角速度;G为引力常数)
人若在地球表面上做测量G值的卡文迪许实验,此时d 与r0几乎相等,测量用的小球可视为贴地球表面的两个小卫星,其公转角速度等于地球自转角速度,在此情况下,整理方程式(3)、(4)、(5),得引力常数G与地球惯性质量、半径、及自转角速度有关,此时(R小于等于R0的情况)引力常数G可以表达为下式:
同理,整理方程式(3)、(4)、(5),得出提供转动惯量的地球惯性质量m与下列参数有关:
分析式(7),地球为非理想圆形球体,是两极稍扁平的椭圆球体,因此北极与赤道两位置的r0、g都是不相等的,同时地球惯性质量分布不均匀,式(7)中出现了4个变量m、g、r0、ω0,现在北极与赤道g、r0、ω0的值已测量出来,我们通过式(7)先计算此两处的变量m,见表3。

表3 某位置提供转动惯量的惯性质量m计算值
表3里变量已得出数值,通过式(6)计算引力常数的值,见表4。
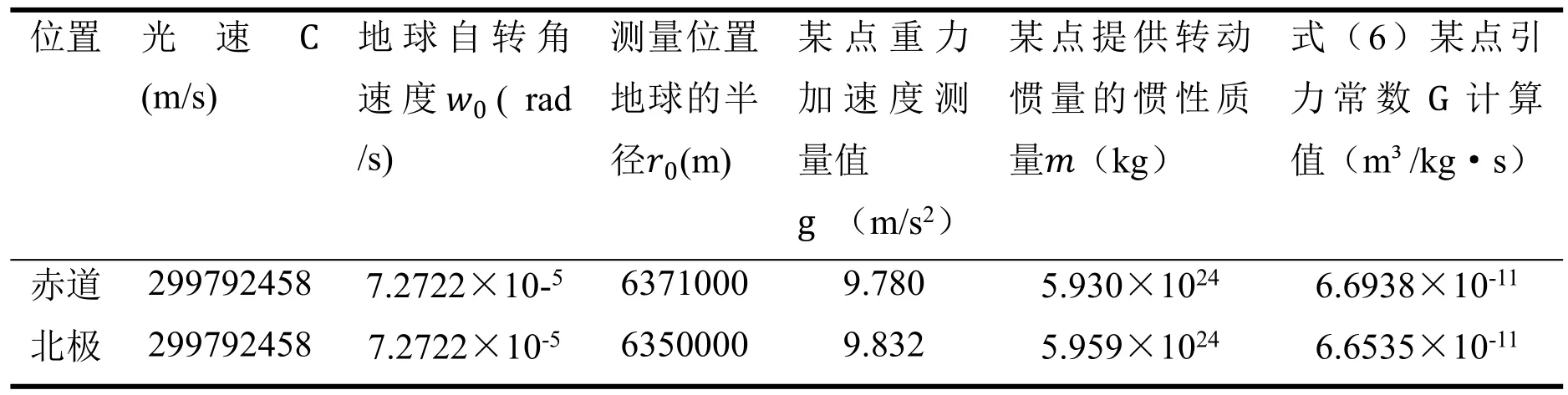
表4 地球不同位置处式(6)计算引力常数G的值
2 讨论
根据表4计算结果,计算得出的G值在6.6535×10-11至6.6938×10-11(m³/kg·s)范围内变化,根据加州理工学院科学家安德森2015年发现的现象,地球的每天时长(简称LOD)周期为5.9年,波动周期与G值的周期一致,G值5.9年的振荡周期与地球的自转速率相配合,自转速率与G值成正比,而地球自转速率由LOD测量值决定。LOD和G值密切相关,安德森注意到LOD的增大的变化幅值为3.47×10-9(rad/s)时,G值的平均增大变化幅值ΔG/G为2.4×10-4(m³/kg·s)。[5]上述式(6)显示,G值对自转速度非常敏感,当知道自转速度增大的变化幅值为3.47×10-9时,还需要知道变量,才能计算变量、假设地球内部质量分布不变(m不变),北极此时的瞬时加速度将增加至9.841(m/s2)计算值,对应的G值增大的变化幅值ΔG/G为9.5475×10-4(m³/kg·s),这变化幅值不符合观测到的数据。但将的变量因素同时增加进去式(6),式(6)表达形式可变为具有4个变量的方程:G=,当实验测量地点不变,式中m、g、r0是几乎不变的,式中项的总值可认为保持不变或变化不大,此时地球自转速度的增大变化幅值为3.47×10-9时,对应的G值增大的变化幅值ΔG/G理论计算值为2.386×10-4(m³/kg·s),接近科学家安德森通过LOD观测到的平均变化幅值2.4×10-4(m³/kg·s)。
3 结论
从质量增量上查找影响引力常数G 测量值的各个参数,发现地球上G值测量实验位置的地球半径、提供转动惯量的惯性质量、地球自转角速度 与之关联,数学表达式为上述式(6),为引力常数G的测量值提供一种理论计算上的参考方法,同时比较符合近期发现的引力常数测量值与地球的自转速率相配合的现象;在质量增量弯曲了引力空间的观点上,找到两者对应的其中一个数值联系,数学表达式为上述式(3)。

