具有混合流道的玄武岩纤维束蓄热体传热分析

徐静文， 匡 荛

(东南大学 江苏省太阳能技术重点实验室， 南京 210096)

在太阳能热电站[1]、乏风瓦斯发电系统[2-3]中，蓄热体是最关键的传热部件。蓄热体和气体在流道内完成热交换后产生高温烟气，高温烟气继续供给余热发电锅炉从而将热能转化成高品质的电能[4]。蓄热体的传热性能影响高温烟气的产生效率和质量，因此对蓄热体传热性能进行优化，能够带来可观的经济效益。

陶瓷蜂窝蓄热体因其结构简单、维护方便、使用成本低等特性而被广泛应用，但是仍存在某些局限。陶瓷蜂窝蓄热体普遍使用纵掠结构[5-6]，气体在笔直的流道中受到的扰动较弱，换热较慢。若使用较大气体流速会导致换热不充分，气体在尚未充分加热时就会被排出。陶瓷蜂窝蓄热体常采用较小的蜂窝孔径(1.5～4.0 mm)[7]，其内部流道单一且狭窄，气体在流道内的流阻较大。在狭窄的流道中，气体以较高的速度流动时，会产生较大的压降。为了在可承受的压降范围内达到较好的传热效果，气体的入口流速一般控制在0.2～2.6 m/s[8]。GOSIEWSKI K等[9]在使用3 mm孔径的陶瓷蜂窝蓄热体时，采用0.823 m/s的气体流速，压降已达近2 000 Pa，若继续增大流速会使得压降急剧增大而超出合理范畴。流速受限使得陶瓷蜂窝热力氧化器在单位时间内的气体处理量不大。

综上，陶瓷蜂窝蓄热体在具有较高的经济性的同时，仍存在如下缺陷：

(1) 采用纵掠结构，对气体扰动较弱,换热较慢，限制了气体的流速。

(2) 采用狭窄且单一的流道，导致压降过大，限制了气体的流速。

笔者针对上述两项问题，提出了一种具有混合流道的玄武岩纤维束蓄热体。纤维束器件群以横掠的方式进行安装固定，混合流道中的次级流道负责与气体进行快速换热，主流道负责将换热完成的气体快速排出。笔者通过数值模拟分析了纤维束排列方式、流道间距等对该蓄热体传热性能的影响。

1 蓄热体物理模型

1.1 蓄热体材料

玄武岩材料属于非晶体，在高温下会熔融成玻璃态，易被拉丝成纤维。此外，玄武岩耐热性能好，具有较高的比热容和优秀的力学性能[10]。因此，笔者选择玄武岩材料作为制作蓄热体中纤维束的原材料。

大量细小的玄武岩纤维丝可通过加捻的方式组合在一起构成直径为d的玄武岩纤维束。在蓄热体中，玄武岩纤维束的两端需要被固定，使其张紧。以纤维为基本单元的编织型器件是典型的低维度器件，每根纤维丝的尺度小，毕渥数低，其导热热阻可以忽略不计，热量损失小。当气体流经纤维束表面时，大量纤维束对气体进行切割、扰动，从而达到较好的传热效果。

1.2 蓄热体结构

玄武岩纤维束以叉排或者顺排的方式排成的纤维束器件群见图1。每个纤维束器件群以叉排的排列方式进行排列，构成了玄武岩纤维束蓄热体(见图2)。

图1 玄武岩纤维束器件群结构立体图

图2 玄武岩纤维束蓄热体结构立体图

为了同时兼顾减小流动阻力与强化传热效果的目的，采用混合流道结构。纤维束器件群的内部由各个细小的纤维束划分成大量小流道，构成次级流道。次级流道的间隙小，其内气体能够和玄武岩纤维进行快速换热，但次级流道内流阻较大。因此，额外增设一个低流阻的主流道。纤维束器件群之间的间隙较大，构成一个低流阻的主流道，可以用于快速排出次级流道内已完成流固表面换热的气体。

1.3 蓄热体二维模型

在模拟分析中，假设气体受到的重力影响可以忽略不计。玄武岩纤维束蓄热体结构平面图见图3。其中，S1为相邻两个纤维束垂直于气体流动方向的距离，S2为相邻两个纤维束平行于气体流动方向的距离，S1和S2为待优化参数。由于蓄热室内结构具有对称性和重复性，使用图3(a)所示的截面进行模拟分析和论证。

图3 玄武岩纤维束蓄热体结构平面图

在图3(a)中，气体自左向右流动，30排纤维束器件群以叉排方式排列，每个纤维束器件群由19列纤维束组成。由于对称性，只需使用一半上下两层叉排排列的纤维束器件群进行模拟分析和论证。图3(b)给出了以叉排排列的纤维束构成的纤维束器件群的半截面，图3(c)给出了以顺排排列的纤维束构成的纤维束器件群的半截面。

两个相邻纤维束器件群在平行于气体流动方向的距离等于每个纤维束器件群的平行于气体流动方向的轴长，两个相邻纤维束器件群在垂直于气体流动方向的距离等于每个纤维束器件群的垂直于气体流动方向的轴长。

2 数值计算

玄武岩纤维向气体的放热过程是一个非稳态的传热过程。模拟过程中，选择空气作为受热流体，玄武岩纤维的初始温度为1 030 K，空气的初始温度为298 K，蓄热体入口处气体的流速为2 m/s。在每个纤维束旁设置一条监控线来测量次级流道中的气体流速，在出口处设置一条监控线来测量气体的出口温度。采用瞬态分析法对放热过程进行计算，计算持续1 000 s。空气和玄武岩的物性参数见表1和表2，其中，t代表热力学温度，K。

表1 空气物性参数

表2 玄武岩物性参数

模拟过程中，纤维束的直径为3 mm，纤维束器件群的排列方式固定为叉排排列，每条流道内，纤维束器件群的排数为30。在纤维束器件群中，纤维束之间的间距和纤维束的排列方式由模拟分析确定。若纤维束器件群内纤维束叉排排列，每列纤维束数量分别为5、10、13、14、17、18、17、18、19、18、19、18、17、18、17、14、13、10、3；若纤维束器件群内纤维束顺排排列，每列纤维束数量分别为5、9、13、15、15、17、17、19、19、19、19、19、17、17、15、15、13、9、5。

蓄热体的热量传递给气体，当气体温度高于温度阈值时，可认为该高温气体可用于余热锅炉发电。此处定义有效放热热量为被加热后温度超过675 K的这部分气体所接收到的来自蓄热体的总热量；定义有效放热时间为蓄热体排出气体温度高于675 K的总时间；定义平均有效放热功率为有效放热热量和有效放热时间的比值。在图3(a)所示的二维模型的模拟过程中，能量及功率的计算都以0.5 m的纤维束进行换算。定义次级流道中大于2 m/s流速占比为次级流道的监控线上的平均流速大于2 m/s的监控线数量占总监控线数量的百分比。

3 结果与分析

3.1 纤维束排列方式对传热的影响

图4为5种相邻纤维束间距方案下的平均有效放热功率和有效放热时间，其中各方案的相邻纤维束间距设置由表3给出。

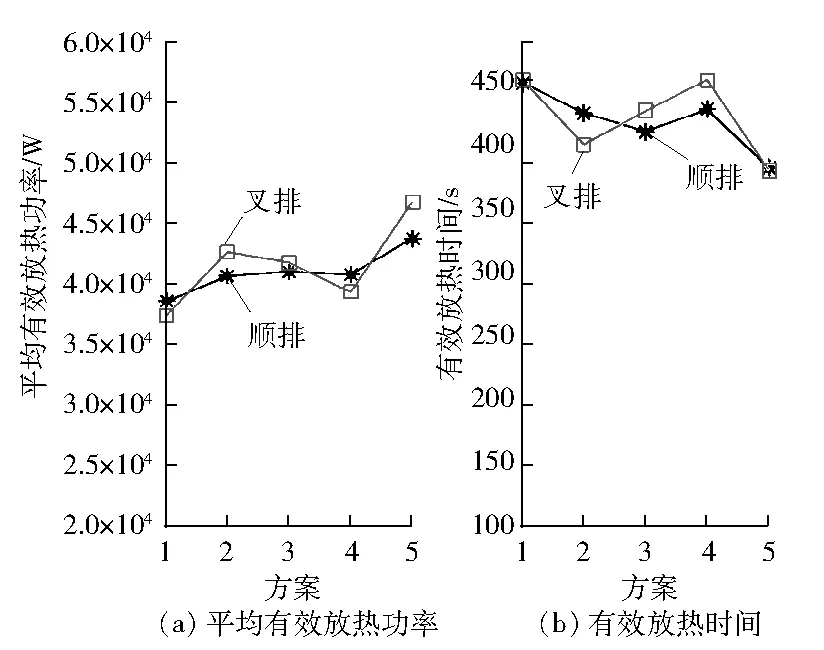
图4 不同方案的平均有效放热功率和有效放热时间

表3 不同方案相邻纤维束间距设置

由图4可以看出：纤维束器件群中纤维束的排列方式对平均有效放热功率和有效放热时间的影响较小；而相邻纤维束间距变化对平均有效放热功率和有效放热时间有显著影响。因此，在寻找具有最优传热效果蓄热体结构参数配置时，可以将纤维束器件群中的纤维束固定为顺排方式排列。

3.2 纤维束间距对传热影响

图5为在固定纤维束器件群中的纤维束为顺排排列，固定S1为7.2 mm，不同S2工况下的平均有效放热功率和放热时间的变化。由图5可以看出：S2的变化对于平均有效放热功率和有效放热时间的影响较小(10%以内)。因此，可以在工程制作中允许的间距范围内，选择较小的S2，以保证蓄热体具有较小的体积。

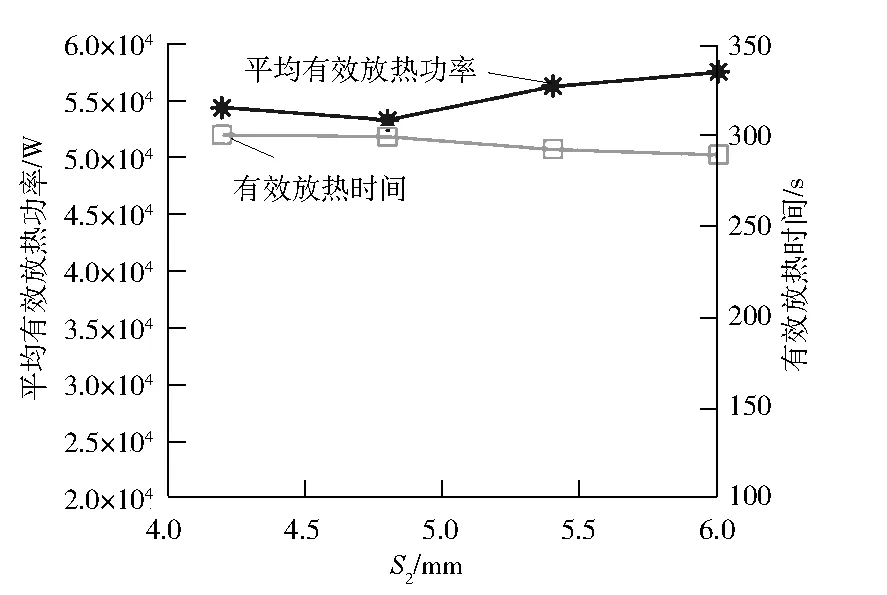
图5 不同S2工况下平均有效放热功率和有效放热时间

图6为在固定纤维束为顺排排列，固定S2为4.2 mm，不同S1工况下的平均有效放热功率和放热时间的变化。

由图6可以看出：当S1增大时，平均有效放热功率显著增大；平均有效放热功率越大，有效放热时间越短。这表明在具有相同热量的蓄热体和气体进行传热时，平均有效放热功率越大，有效放热时间也会随之缩短，可以更快地完成放热，传热效果越好。当S1增大的同时，安装相同数量纤维束的蓄热体的体积也会随之增大。因此，需要在体积允许的范围内，通过增大S1来获得更好的传热效果。

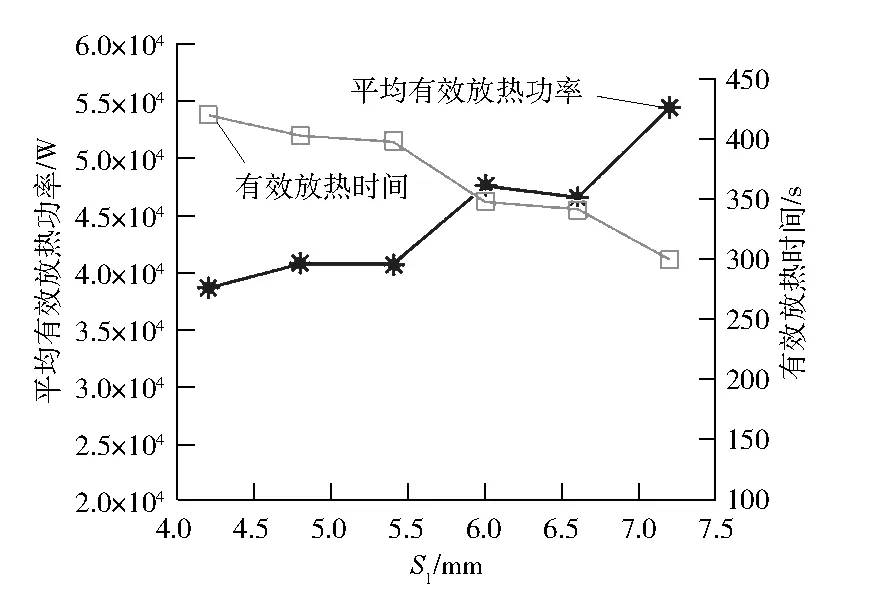
图6 不同S1工况下平均有效放热功率和有效放热时间

通过上述模拟结果可知，当纤维束器件群中的纤维束以顺排方式排列，S1取7.2 mm、S2取4.2 mm时，具有混合流道的纤维束蓄热体可以获得较好的传热效果。

3.3 次级流道气体流速与传热效果的关系

图7给出了不同工况下，平均有效放热功率和次级流道中气体流速占比，其中各方案的相邻纤维束间距设置见表3。由图7可以看出：次级流道中流速大于2 m/s的气体占比越高，则平均有效放热功率越大。这表明，次级流道的气体流通状态影响了传热的快慢，当次级流道中气体处于高流速的占比越小，次级流道越阻塞，越不利于强化传热。

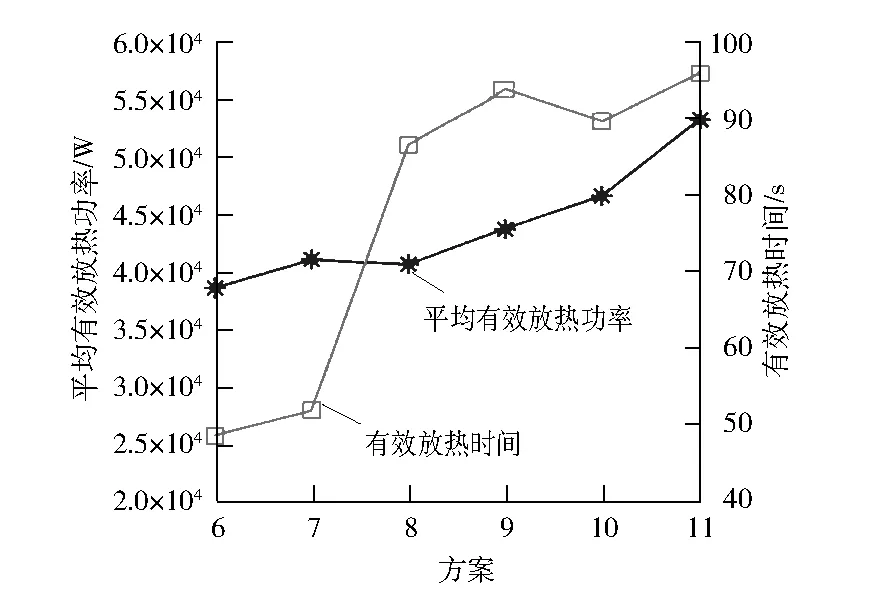
图7 不同方案的平均有效放热功率和次级流道流速关系

3.4 蓄热体性能比较

纤维束器件群中纤维束以顺排排列，S1取7.2 mm、S2取4.2 mm，蓄热体的总长度为2.36 m，总体积为0.156 m3。当入口气体流速为4 m/s时，单位长度蓄热体的压降为882 Pa。文献[9]中的陶瓷蜂窝蓄热体使用3 mm孔径，蓄热体总长度2 m，总体积为0.405 m3。当入口气体流速为0.823 m/s时，其单位长度蓄热体的压降已经接近1 000 Pa。该玄武岩纤维束蓄热体的有效传热效率为78.3%，而文献[1]中的陶瓷蜂窝蓄热体有效传热效率小于60%。因此，该玄武岩纤维束蓄热体在保证较小的压降和有效传热效率的同时，可以使用更大的气体流速。

4 结语

通过对具有混合流道的玄武岩纤维束蓄热体的传热性能进行的模拟分析，可以得到以下结论：

(1) 在不同的间距方案中由排列方式的变化所带来的有效放热功率相差不大，但各有优劣。因此，可在选定间距方案后再根据模拟结果选择合适的排列方式。

(2) 具有混合流道的玄武岩纤维束蓄热体的传热效果随S2的增大而轻微增大，在实际应用中可选取较小的S2，以保证较小的蓄热体体积。

(3) 通过增大纤维束器件群的S1，可以获得显著增高的平均有效放热功率，在体积允许的前提下，可选取较大的S1。

(4) 具有混合流道的玄武岩纤维束蓄热体的次级流道中高流速气体的占比和蓄热体传热效果呈正相关。

(5) 具有混合流道的玄武岩纤维束蓄热体相比于传统陶瓷蜂窝蓄热体，在保证有效传热和压降的前提下，能使用较大的气体流速，具有更高的有效传热效率。