一种GEO卫星太阳光遮挡轨迹设计与控制方法
黎 飞,雷拥军,2,冯佳佳
(1. 北京控制工程研究所,北京 100094; 2. 空间智能控制技术重点实验室,北京 100094)
0 引 言
地球静止轨道(GEO)是一条重要的空间经济走廊,世界主要航天大国均部署有高价值GEO卫星,这些卫星可为地面用户提供连续、稳定的各种服务,在国民经济建设以及国防安全领域发挥着重要的作用。
自2006年以来,美国为保持航天领域的领先地位,在多个高轨空间态势感知项目的牵引下,发射了一系列高轨小型卫星,包括2颗“微卫星技术试验”(MiTEx)卫星,4颗“地球同步轨道空间态势感知计划”(GSSAP)卫星,1颗“增强的地球同步轨道实验室”(EAGLE)飞行器及其携带的3颗100 kg级子卫星等。这些卫星采用不同技术手段来获取GEO目标物体的信息和数据,并且具备对GEO卫星进行交会与抵近操作的能力,可对他国的空间安全造成一定程度的威胁。激烈的天基空间攻防态势已经存在并将一直持续下去,因此,开发先进的空间攻防系统和技术,保护国家重要空间资产安全,具有重要的经济和军事价值。
目前,国内外对空间攻防技术的研究主要集中在空间打击领域,包括空间拦截、在轨抓捕、聚光烧毁等。这些技术以破坏卫星功能、甚至物理摧毁卫星为目标,具有较强的毁伤能力和威慑作用,一旦实施打击即意味着战争的发生。在和平时期,为应对复杂的空间攻防态势,降低战争发生的风险,需要发展具备警示和驱离、并且不进行物理摧毁的攻防技术。电磁干扰、网络攻击等软杀伤手段,可在一定时间内使目标卫星丧失正常工作能力,而不对卫星造成实际物理伤害,可有效避免热冲突,是和平时期主要的攻防手段。
本文从航天器能源安全的角度出发,针对地球静止轨道卫星,提出一种基于太阳光遮挡的远距离空间攻防方法。该方法利用遮阳物体对目标卫星的太阳光进行遮挡,短时间可造成目标卫星能源不足、部分功能失效,达到警示和驱离作用。由于航天器和太阳光位置实时变化,需要对航天器间的相对运动轨迹进行特殊设计。
在基于近圆轨道的相对运动问题研究中,主要采用C-W方程进行相对运动轨迹的设计。文献[9]提出了双椭圆绕飞轨迹,并在离散空间设计了最优跟踪控制律。文献[10]研究了绕飞卫星对运行在圆轨道或椭圆轨道上的目标航天器进行共面或异面快速绕飞的轨迹设计与制导问题。文献[11]进行了单脉冲“水滴”形、多脉冲受限圆形和“田径场”形等多种绕飞构型的设计。文献[12]针对在轨服务任务对绕飞技术的要求,提出了单水滴绕飞构型、双水滴拼接绕飞构型。文献[13]提出了基于C-W方程的多脉冲空间悬停的控制方法,实现了主动航天器在目标航天器附近任意点的近似稳定悬停。文献[14]研究了“雨滴”悬停构型的形成机理以及基于Lambert转移的悬停构型移动控制策略。
上述文献对航天器相对运动轨迹的各类构型进行了研究,但均不适合两航天器间进行太阳光遮挡这一类问题。因此,本文的出发点具有一定的创新性。本文安排如下:
首先,对空间太阳光遮挡原理进行分析,得到遮挡精度与两航天器之间距离的关系,并指出相对运动轨迹受圆锥面的约束。
其次,根据近圆轨道相对运动方程,设计了圆锥面绕飞轨迹和连续推力制导律,将投影在轨道平面内的相对运动轨迹划分为等份,推导了一整圈绕飞机动的速度增量需求。在考虑非线性误差和地球非球形摄动等空间环境影响后,仿真表明开环条件下的遮挡控制精度较差,不满足预期的遮挡要求。
最后,将相对动力学方程改写为状态空间方程,采用自抗扰控制方法,对圆锥面绕飞轨迹进行闭环控制,遮挡控制精度可以达到米级的水平,具有一定的实用价值。
1 太阳光遮挡运动分析
太阳光在空间环境中为平行光,当太阳、追踪航天器与目标航天器处于同一条直线,且追踪航天器携带较大面积的遮阳物体时,理论上可以切断目标航天器的太阳光能源供应。
如图1所示,假设目标航天器太阳帆板展开后的最大尺寸为,追踪航天器遮阳物体长度(或直径)为,两航天器间相对距离为。为保证太阳光遮挡精度,追踪航天器质心到太阳与目标航天器之间连线的垂直距离应控制在(-)2内,则追踪航天器与太阳矢量的夹角满足如下关系:
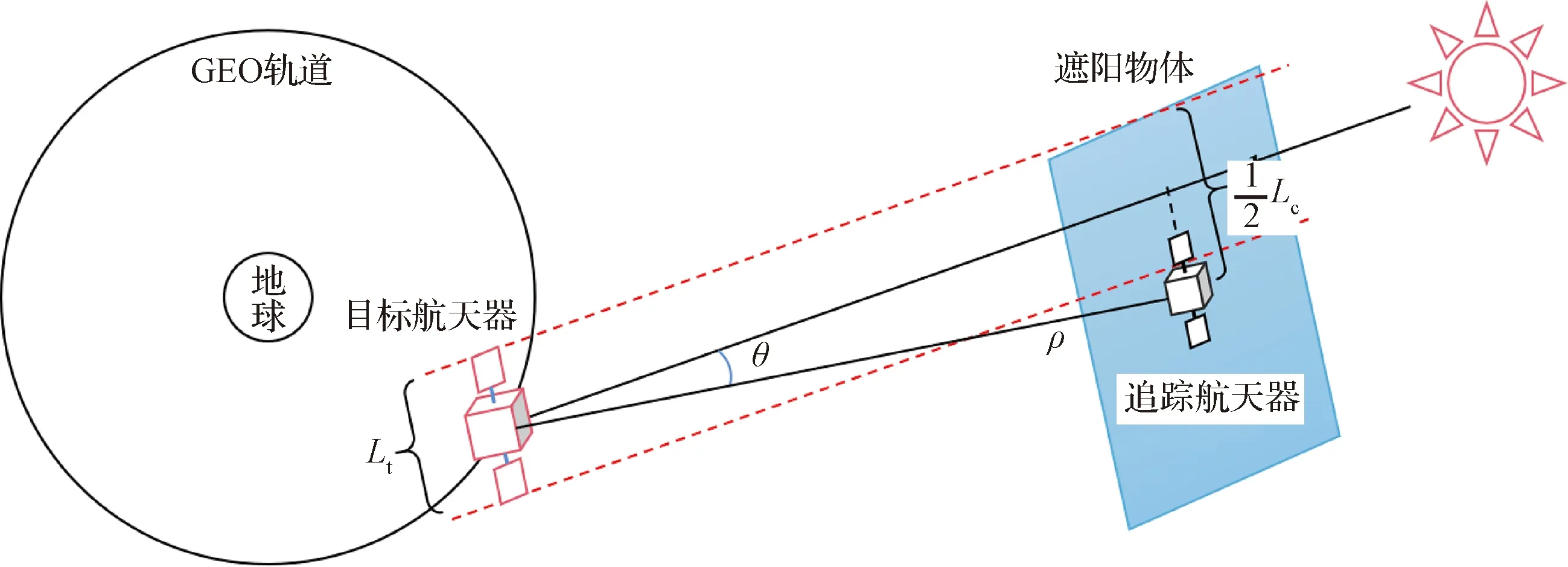
图1 GEO卫星遮挡太阳光的示意图Fig.1 A diagram of the GEO satellite shielding the Sun
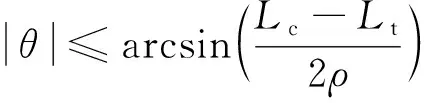
由上式可知,在控制误差不变的条件下,随着两航天器之间的距离增大,要求夹角相应地减小,增加了相对运动控制难度。
由于黄赤交角的存在,太阳矢量与地球赤道平面的夹角(即太阳高度角)在±23°26′之间呈现周年变化,且每日的太阳高度角变化量与日地空间位置有关。图2所示为2021年太阳高度角及其变化率曲线,可知在春、秋分时,太阳高度角在0附近,且太阳高度角变化率最大,约为0.4°/日;在夏、冬至时,太阳高度角达到最大,但太阳高度角变化率最小,约为0°/日。

图2 2021年太阳高度角及其变化率Fig.2 The curves of solar altitude angle and its change in 2021
太阳高度角较小时,太阳矢量相对GEO卫星的运动近似为匀速圆周运动,可以设计同一平面内的圆形受迫绕飞轨迹,使得追踪航天器持续遮挡太阳光。一年中的大多数时间,太阳矢量与地球赤道平面存在一定的夹角,而且在一天之中一直处于地球赤道平面的上方或下方,可知,太阳矢量在目标航天器的轨道坐标系中扫过的曲面近似为圆锥面,如图3所示。

图3 太阳矢量圆锥面运动Fig.3 The conical motion of the solar vector
为描述追踪航天器相对目标航天器的运动轨迹,通常建立以目标航天器为原点的参考坐标系,其中,轴从目标航天器指向地心,轴在轨道面内,垂直轴指向运动方向,轴由右手定则确定。也称为目标航天器的轨道坐标系。
为使追踪航天器在一个完整的恒星日持续遮挡太阳光,其运动轨迹应受圆锥曲面约束,同时在平面的投影角速度应与地球自转角速度一致。圆锥曲面方程为:
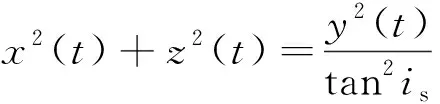
(1)
式中:()、()、()为相对运动轨迹在目标航天器轨道坐标系中的坐标;为该恒星日内太阳高度角的平均值。
2 相对运动轨迹设计
2.1 相对运动方程
当目标航天器运行于圆或近圆轨道,且两航天器间的距离较近时,忽略高阶项和各种摄动影响,得到线性的相对运动方程,即如下的Hill方程:

(2)
式中:为目标航天器的平均轨道角速度;=[,,]为施加在追踪航天器上的三轴控制加速度。
从式(2)可知,轨道平面内(平面)的相对运动不含轴分量,因此与轨道平面外的相对运动(轴方向)是相互独立的。
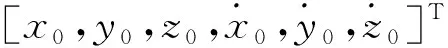

(3)


(4)
式中:

分析表明,满足一定初始条件时,即=0,追踪航天器投影到平面内的运动轨迹为长半轴等于2倍短半轴的封闭椭圆,轨迹周期与目标航天器轨道周期相同。由于椭圆轨迹的角速度不是匀速的,不满足追踪航天器持续遮挡太阳光的需求,因此需要设计合适的控制加速度,使绕飞轨迹在平面内具有匀速角速度。
2.2 圆锥面绕飞轨迹设计
取初始时刻=0,追踪航天器位于目标航天器前方或后方距离为的位置,如图3所示,记为[(0),(0),(0)]=[, 0, 0]。


(5)
式中:p为第次正弦运动的时间偏移量,首次脉冲机动时=0。
追踪航天器应选择合适的初始脉冲Δ,使得()大于的时间应足够长,令时刻追踪航天器运行至()=,且太阳矢量也刚好运行至平面,解得:
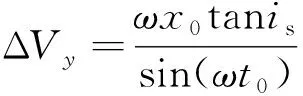
在平面上方或下方,从时刻起追踪航天器开始进行匀速圆周运动,有:

(6)
式中:()为追踪航天器在平面内的投影到坐标系原点的距离,代入式(1),解得:
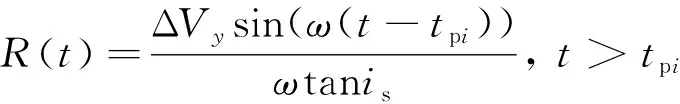
将()代入式(6)中,得到:

(7)
式中:=Δ(2tan)。
由式(7)可知,投影在平面内,追踪航天器的运动轨迹为半径等于的多个拼接圆,其圆心坐标为:
(-sin((-p)),cos((-p)))
对式(5)和(7)求导,得到追踪航天器的相对运动速度和控制加速度分别为:

(8)

(9)


图4 y方向运动轨迹Fig.4 The motion trajectory of y-direction
综上所述,追踪航天器开始轨道机动后,经过一圈受迫圆锥面绕飞再回到初始位置,需要经过以下的运动过程:
1) 0时刻,施加初始速度脉冲Δ,追踪航天器开始在轴上进行正弦曲线运动;

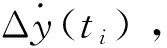
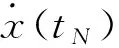

在整个绕飞机动过程中,需要实施多次速度脉冲机动,以时刻为例,速度增量计算方法如下:
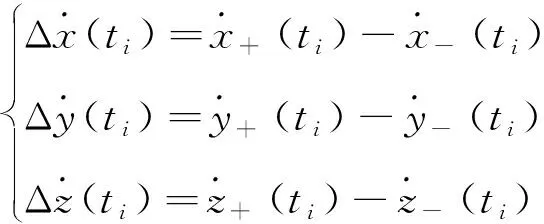
(10)
式中:
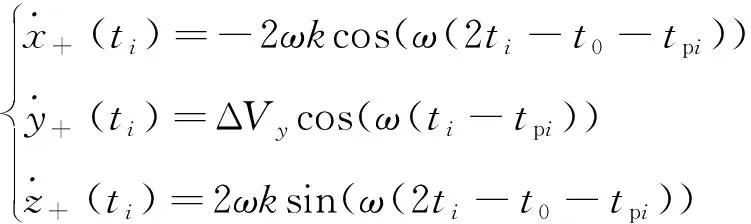

2.3 燃料消耗分析
燃耗可用一个绕飞周期内的总速度增量Δ来表示,即:


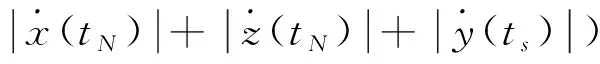
(11)
为得到Δ的显示表达式,并进行燃耗趋势分析,将至之间的阳光遮挡轨迹分为(≥3)等份,则有以下关系式:



代入式(11),并记=π,整理得到:



(12)
式中:mod(,)为正整数模除函数,即由除以得到的余数,round()为四舍五入函数。
固定和,可知Δ()是自变量的离散函数,难以通过解析方法求取导数以分析其变化趋势,取=20°,=7.292116×10rad/s,=1 km,绘制关于的曲线,如图5所示。

图5 总速度增量曲线Fig.5 The curve of total velocity increment
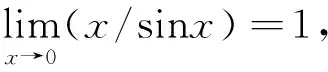

(13)
从图5和式(13)可知,当遮挡段数增大时,燃料消耗逐渐减小;当增大到一定程度时,燃料消耗近似为一极限值。另一方面,较大时,需要进行的三轴速度脉冲机动次数较多,相应地增加了控制难度。因此,在实际的工程应用中,应综合考虑燃料消耗和控制难易程度,选择合适的脉冲段数来实施阳光遮挡。
2.4 圆锥面绕飞开环仿真
两航天器的初始轨道参数如表1所示,可知初始相对位置为[-80950, 0, -00073]km,太阳高度角平均值取=11.4°。

表1 两航天器的初始轨道根数Table 1 The initial orbits of the two spacecraft
取目标航天器受太阳辐射的面积为80 m,最大长度为=40 m,质量为5000 kg,则面积质量比(简称面质比)为0.016。设相对运动轨迹控制误差小于10 m,由第1节可知,追踪航天器遮阳物体的长度应为≥60 m。遮阳物体面积分别取600 m和1800 m,为减少推进剂消耗,追踪航天器一般为质量较小的卫星,本文取其质量为2000 kg,则面质比为0.3和0.9。为便于比较,增加一组面质比为0.06的仿真工况。
取仿真步长为1 s,遮挡段数为=8,同时考虑地球非球形摄动、日月引力和太阳光压等空间环境的影响,仿真结果如图6~图7所示。其中,图6所示为相对运动轨迹在平面的投影视图,图7所示为相对运动轨迹的跟踪误差曲线。
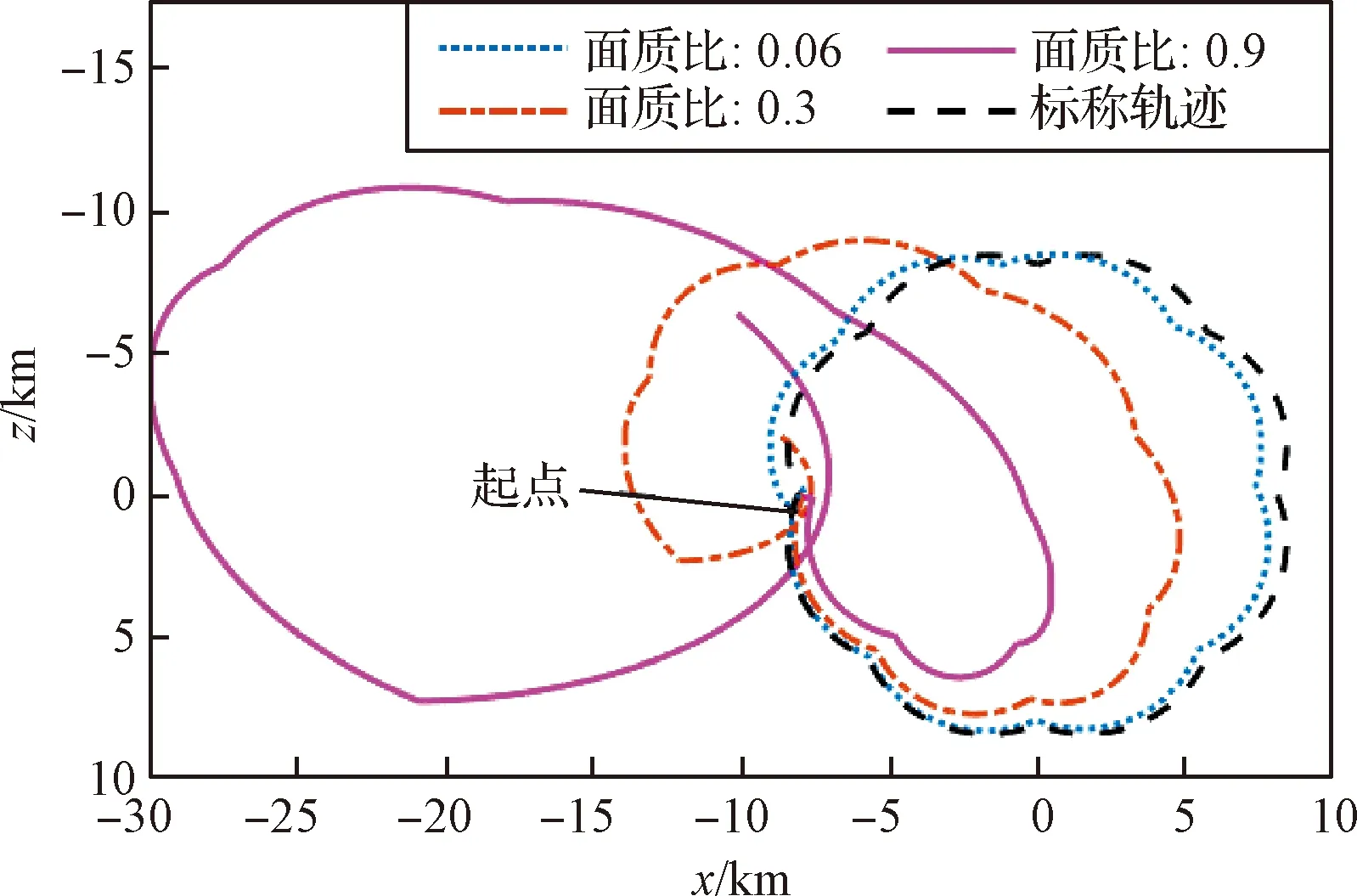
图6 开环控制下相对运动轨迹在XOZ平面的投影Fig.6 Projection of relative trajectories in the XOZ plane under the open loop control
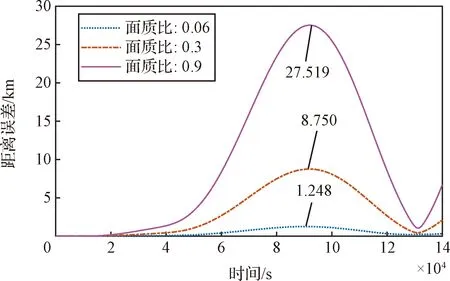
图7 开环控制下相对运动轨迹的距离误差Fig.7 The distance error of relative trajectories under the open loop control
由图6~图7可知,随着面质比的增大,相对运动轨迹偏离标称轨迹的距离相应增大。对于面质比最小的工况,误差最大也能达到km级别,远大于目标误差10 m的要求,表明开环条件下按照既定的解析解策略,无法持续遮挡目标航天器的太阳光。
式(2)为基于圆参考轨道、线性化、无摄动假设得到的,而本节仿真考虑了非线性特性和摄动影响,可以得到以下结论。
1)非线性特性与两航天器间的距离有关,距离越远作用越大,当初始相对位置与GEO轨道半长轴相比为小量时,非线性特性对相对运动的影响较小。
2)非球形引力摄动和日月引力摄动只与卫星位置有关,而与卫星质量无关,将两航天器作为一个整体考虑时,其对相对运动轨迹的影响较小。
3)光压摄动比非球形引力摄动和日月引力摄动小一个量级,但与卫星面质比成正比关系。由本节仿真条件可知,追踪航天器的面质比比目标航天器大一到两个量级,使得光压差持续影响相对运动轨迹,成为相对运动轨迹误差的主要因素。
综上所述,基于解析方法得到的控制加速度使得控制误差较大。为减小相对运动误差,需要设计合适的闭环控制策略。
3 基于自抗扰的闭环控制
3.1 闭环控制律设计
本文采用自抗扰控制方法来设计闭环控制律。考虑非线性误差和空间环境摄动,式(2)改写为:
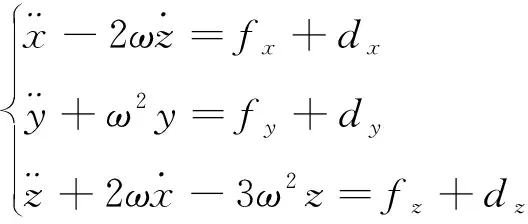
(14)
式中:=[,,]为非线性误差和空间环境摄动之和。
记


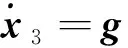

(15)
式中:

其中:为3阶单位阵。
为估计总干扰,设计线性扩张状态观测器(LESO)为:
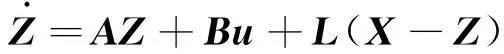
(16)



(17)



3.2 圆锥面绕飞闭环仿真
闭环仿真初始条件和卫星质量、面积参数同2.4节,遮挡段数为8,面质比选取最大的工况,即0.9。观测器带宽和控制器带宽分别取为:=009,=003,闭环仿真结果如图8~图9所示。

图8 闭环控制下相对运动轨迹的3D视图Fig.8 3D view of relative motion trajectories under the closed loop control

图9 闭环控制下相对运动轨迹的距离误差Fig.9 The distance error of relative trajectory under the closed loop control
由图8和图9可知,闭环控制下,追踪航天器在圆锥面上形成的轨迹为一对称的封闭曲线,相对运动轨迹误差小于10 m,具有较高的控制精度,满足持续遮挡太阳光的要求。与图7相比,仅在轴实施速度脉冲机动时,距离误差有小幅波动,并未出现开环控制误差累积变大的现象。
合理增大观测器带宽和控制器带宽,可以进一步减小跟踪误差,但也导致总速度增量的增加,因此在实际应用中,需要根据误差要求选取合适的观测器和控制器参数。此外,闭环控制下需要追踪航天器配置可实时获取自身轨道或相对目标航天器位置信息的测量部件,如导航敏感器或激光测距仪,一定程度上增加了系统成本。
4 结 论
本文阐述了利用太阳光遮挡来进行GEO卫星空间攻防的工作原理,研究了基于C-W方程的圆锥面受迫绕飞问题,推导了段遮挡轨迹下的燃料消耗表达式。仿真结果表明,在非线性误差和空间环境摄动的影响下,开环条件下的相对运动跟踪误差较大,并主要受太阳光压差的影响,不满足持续遮挡太阳光的要求。引入自抗扰控制律后,克服了相对运动模型不确定性和外部干扰,提高了相对轨迹控制精度,使得基于太阳光遮挡的空间攻防系统具有一定的实用价值。
本文设计的圆锥面绕飞轨迹将太阳高度角取为平均值,而实际的太阳高度角在一天之中是实时变化的,因此本文的圆锥面轨迹存在一定的系统误差,需要进行相应的修正,修正方法将在后续的研究中予以考虑。

