等离子体包围的球对称黑洞解

李强 王焘

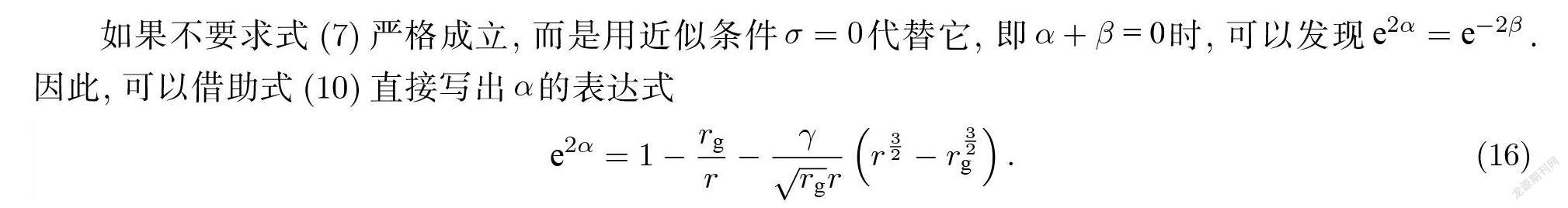
摘要： 考虑静态、球对称的情况 ， 对等离子体包围的黑洞外部解进行了细致研究.在给出基本方程之后 ， 分别求出了在gttgrr =  1和 p =0 两种近似条件下对应的解析解. 与精确数值解进行了比较 ， 发现前一种近似条件下的解析解更接近精确数值解.这为在等离子体包围的情况下计算黑洞扰动的似正规模 ， 以及研究黑洞阴影和光子环提供了依据.

关键词：黑洞解;  广义相对论;  黑洞阴影

中图分类号： O412.1    文献标志码： A    DOI： 10.3969/j.issn.1000-5641.2022.02.013

Spherically symmetric solutions for a black hole surrounded by plasma

LI Qiang，  WANG Tao

（School of Physics and Electronic Science， East China Normal University， Shanghai  200241， China）

Abstract： In this paper， the exterior solution for a spherically symmetric black hole surrounded by plasma is studied in detail. After deriving the fundamental governing equations， the analytic solutions under two approximate  conditions，  gttgrr =  1 and p =0 ，  are  investigated. Comparing  the  two  results  with  the accurate numerical solution， we find that the former approximation offers superior accuracy. This provides a basis for studying the quasinormal modes of perturbations as well as the shadow and ring when the black hole is surrounded by plasma.

Keywords： black hole solutions;  general relativity;  shadow of black hole

0  引言

在研究许多物理问题的时候 ， 如计算黑洞扰动的似正规模时、研究黑洞阴影和光子环时 ， 都需要先知道度规的解析表达式.在真空中 ， 球对称的黑洞可以用史瓦西解来描述.在非真空的情况下 ， 如黑洞周围有暗物质时 ， 史瓦西解则只能描述黑洞的内部 ， 不能精确地描述黑洞的外部.这是因为 ， 黑洞外部的暗物质改变了黑洞外部的引力场 ， 从而改变了黑洞外部的度规. 近些年来 ， 关于暗物质包围的黑洞解的研究已经取得了较大的进展[1-2] ， 这些解的具体形式都取决于暗物质的密度分布和状态方程.

黑洞在形成和生长的过程中 ， 吸积盘中会留下大量的等离子体 ， 所以天体物理中的黑洞绝大多数都是被等离子体包围的.由于等离子体的密度分布不同于暗物质的密度分布 ， 可以推断 ， 相应的外部解也不相同.目前 ， 关于等离子体包围的黑洞解还未见相关研究的报道.本文考虑静态并且球对称的情况 ， 采用解析和数值两种手段 ， 求出等离子体包围的黑洞外部解.在实际应用中 ， 这种解可以近似地描述具有几何厚光学薄的热盘[3]、旋转较慢的黑洞的外部时空.

本文后续内容安排：第 1章列出静态球对称度规应满足的引力场方程 ， 并将它们整理成便于求解的形式;第 2章给出等离子体的密度分布 ， 并求出一部分度规分量的解析表达式;第 3章采用两种不同的近似条件 ， 求出剩余度规分量的解析表达式 ， 然后用数值方法得出精确解的函数图像;第 4章是讨论与展望.

为了使表述简明 ， 本文约定光速c =1 ， 黑洞内部由质量为 M 的史瓦西解來描述 ， 对应的视界半径记为rg = 2GM ， 其中 G 为万有引力常数.

1  一般方程

本文考虑质量为 M 的黑洞外部分布有密度为ρ（r）、压强为p （r）的等离子体 ， 并假设等离子体是静态的、球对称分布的理想流体.那么 ， 黑洞外部的度规也是静态的、球对称的 ， 它的一般形式可以由线元

来描述.式 （1）中r ⩾ rg .该度规包含2个未知函数α（r）和β（r） ， 它们必须满足引力场方程（为使方程的数学表达式简洁 ， a（r）、b（r）用 a、b 表示， 下同）

在以上4 个方程中 ， 方程（2）只包含1 个未知函数β（r） ， 并且是一阶微分方程. 可将它直接积分 ， 从而得到

其中， m （r）的表达式为

将式（5）代入式（3）、式（4）， 联立消去p ， 可以得到α（r）满足的方程 ， 具体为（为使数学表达式简洁 ， 用 m 表示 m（r）， 下同）

∂α +（∂rα）2+ 3Gm −4πGr3ρ− r∂rα+ 3Gm −4πGr3ρ= 0.   （7）

原则上 ， 只要知道密度函数ρ（r） ， 就能根据式（6）计算出m （r） ， 然后再分别求解出式（5）的β（r）

和式（7）的α（r）. 当然 ， 其结果往往无法用解析函数表达出来.

2  等离子体包围的黑洞

在黑洞外部r ⩾ rg ， 取等离子体密度函数为[4]

其中 ， γ= 是一个无量纲常数 ， 它正比于黑洞质量吸积率M_A ， 后者不依赖于r .本文考虑静态近似的情况 ， 即忽略M_A 随时间t 的缓慢变化. 将式（8）代入式（6）， 积分后得

再将式（9）这个结果代入式（5）， 得到度规分量grr = e2 的表达式

与之对应有两个视界 ， 由 →0给出：一个是黑洞视界r = rg ;另一个是宇宙视界

对于式（8）给出的密度函数 ， 式（5）是可积的 ， 所以β（r）有解析表达式;但是式（7）却没有解析解 ， 即α （r）没有解析表达式. 为了得到实用的解析解 ， 可以不要求式（7）严格成立 ， 而是用某个近似条件代替它 ， 从而得到α（r）的解析近似表达式. 本文将研究以下两类近似条件.

1）许多球对称黑洞解都满足gttgrr = −1 ， 即α+ β= 0. 在给定密度函数ρ（r）后 ， 文献[1，5]利用这一条件得到了暗物质包围的黑洞解.在 3.1节 ， 本文将用α+ β= 0代替式（7）， 给出相应的α（r）的解析近似表达式.

2）将式（5）代入式（3）， 可以得到α（r）的另一个表达式

它不仅与密度 ρ（r）有关 ， 还依赖于压强 p （r）. 在已知密度函数ρ （r）的情况下 ， 如果不要求式 （7）严格成立 ， 而是根据实际情况写出一个合理的状态方程或者压强函数 p （r） ， 就有希望将式（12）积分 ， 得到α（r）的解析近似表达式.例如 ， 对于低温等离子体[4] ，  ≪1 ， 可以取p （r）= 0进行解析计算.这是3.2节将要研究的内容.

为了精确地比较这两个解析近似解 ， 先定义一个新的函数

然后利用式（2）和式（7）， 推导出σ满足的方程

将式（2）、式（3）两式求和 ， 可以得到状态方程参数w =  的表达式

在3.3节 ， 将求出式 （14）的精确数值解 ， 并以 σ和 w 为标准来评估两个解析近似解的优劣 .

3  两类解析近似解及对比

3.1  σ= 0近似下的解析解

如果不要求式（7）严格成立 ， 而是用近似条件σ= 0代替它 ， 即α+ β= 0時 ， 可以发现 e2  = e −2 .因此， 可以借助式（10）直接写出α的表达式

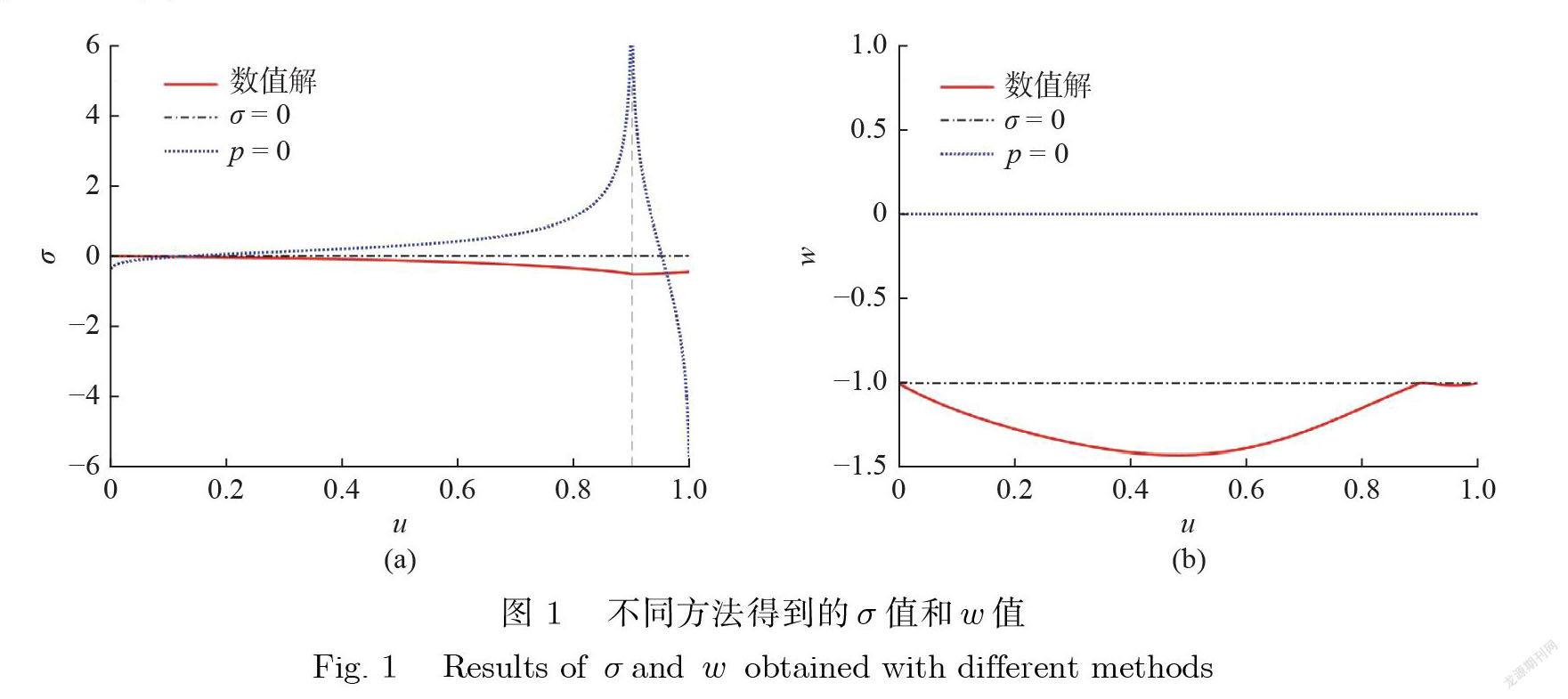
将条件σ= 0代入式（15）， 还可以得到这种情况下的状态方程参数w =− 1. 它们的取值分别对应图1（a）和图1（b）里的点划线.

在黑洞外部 ， 该解的形式与文献[6]中w =− 情况下的解相同.虽然两者具有相同形式的引力场 ， 但它们是由不同的物质场引起的：在文献[6]中， 物质场为暗能量;在本文中， 物质场为等离子体.

3.2  p =0近似下的解析解

黑洞周围的等离子体以质子和电子为主 ， 密度ρ（r）主要来自质子的贡献. 如果质子的温度远低于电子的温度[3] ， 则w ≪1 ， 可以近似地取p =0 .将这一条件和式（9）代入式（12）， 可以发现 ， 在两个视界之间 ， 即rg < r ⩽ rc 的区域 ， 有

超出宇宙视界的范围 ， 即r > rc 时 ， 则有

有了α （r）和 β（r）的解析表达式以后 ， 可以根据定义的式（13）直接求出σ （r）的表达式 ， 其数值见图1（a）中的虚线. 显然 ， 在这种情况下 ， 状态方程参数w =0 ， 即图 1（b）中的虚线.

3.3  与精确数值解对比

最后， 借助计算机 ， 采用数值方法 ， 分别计算σ和w 的精确解.为了便于处理 ， 令

则式（14）可重新写成一个数值上更易于处理的形式 ， 为

通过式（20）， 可以用数值方法先后计算出∂uσ和σ ， 再将∂uσ代入式（15）， 即可计算出 w 的数值. 计算结果见图1（a）和图1（b）里的实线.

从物理上讲 ， p =0近似也是很合理的.我们知道 ， 氢原子的电离能为136 eV ， 而电子的静止能量为 0.511 MeV ， 质子的静止能量为938 MeV .在研究的吸积盘内部 ， 氢原子完全电离成高温电子和低温质子 ， 即氢等离子体.其中电子是相对论性的 ， 质子是非相对论性的.所以等离子体的压强主要由电子的动能产生， 密度主要来自质子的静止能量 ， w ≈  ≈ 0.

图1（a）给出了3 种不同求解方式下σ 的结果 ， 其中 ， 实线、点划线和虚线依次对应精确数值解、σ =0近似解、 p =0近似解.按照相同的约定 ， 图1（b）描出了3 种情况下对应的w 值. 将2 种解析近似结果（分别用点划线和虚线表示）与精确数值解的结果（实线）对比， 可以发现 ， σ= 0近似解与精确数值解更接近 ， 而 p =0近似解则偏离较远. 这里取γ= 0.1 ， 对应图中曲线不连续处u ≈1 −γ 为宇宙视界的位置;如果γ取值更小 ， 则宇宙视界半径更大 ， 图中曲线不连续点右移.

4  讨论与展望

通过对比图1的结果 ， 能够很明显地看出 ， 与 p =0近似解析解相比 ， σ= 0近似解析解更接近精确数值解的结果 ， 即更符合真实情况 ， 这也为我们在另一篇文章中所采用的度规形式提供了支持.

计算黑洞似正规模的方法很多 ， 比较常用的方法有 Wentzel-Kramers-Brilloui （WKB）近似法、渐近迭代法等[7-8]. 在本文中 ， 等离子体包围的黑洞解对史瓦西解的偏离完全由γ 参数来描述. 因此可以推断 ， 黑洞视界外的物质对振荡模式的影响主要由γ值的大小决定 ， 但二者之间的定量关系还值得进一步研究.

本文只考虑了静态分布的等离子体和静态的黑洞外部解. 这对吸积率较小（即γ≪ 1）的黑洞是一个较好的近似.严格来说 ， 如果考虑等离子体的引力效应 ， 那么原来的史瓦西度規应该变成与时间和空间都相关的函数 ， 理由如下：首先 ， 由于吸积盘的存在 ， 黑洞的质量会随着时间的推移逐渐增加;另外 ， 即使不考虑吸积效应 ， 由于来自中心黑洞的引力效应 ， 等离子体也无法保持一个静止的状态. 因此 ， 考虑黑洞周围被等离子体或暗物质包围 ， 谋求含时引力场方程的解析近似解 ， 是一个值得进一步挑战的问题.

[参考文献]

[1] XU Z Y， HOU X， GONG X B， et al. Black hole space-time in dark matter halo [J]. Journal of Cosmology and Astroparticle Physics，2018（9）：038.

[2] XU Z Y， GONG X B， ZHANG S N. Black hole immersed dark matter halo [J]. Physical Review D， 2020， 101（2）：024029.

[3] YUAN F， NARAYAN R. Hot accretion flows around black holes [J]. Annual Review of Astronomy and Astrophysics， 2014， 52：529-588.

[4] PERLICK V， TSUPKO O Y， BISNOVATYI-KOGAN G S. Influence of a plasma on the shadow of a spherically symmetric black hole [J].Physical Review D， 2015， 92（10）：104031.

[5] KONOPLYA R A. Shadow of a black hole surrounded by dark matter [J]. Physics Letters B， 2019， 795：1-6.[6] KISELEV V V. Quintessence and black holes [J]. Classical and Quantum Gravity， 2003， 20（6）：1187.

[7] WU C. Scalar field quasinormal frequencies of Reissner –Nordström black hole surrounded by quintessence by using the continued fractionmethod [J]. International Journal of Modern Physics D， 2017， 26（10）：1750111.

[8] YAN Z N， WU C， GUO W J. Scalar field quasinormal modes of noncommutative high dimensional Schwarzschild-Tangherlini black holespacetime with smeared matter sources [J]. Nuclear Physics B， 2020， 961：115217.

（责任编辑：李艺）