小长径比脉冲管制冷机重力影响的实验研究

张广伟 王乃亮 荀玉强 蔡京辉

（1 中国科学院理化技术研究所,中国科学院空间功热转换技术重点实验室 北京 100190）

（2 中国科学院大学 北京 100049）

1 引 言

小型脉冲管制冷机目前已经广泛应用于航天领域和低温超导领域,主要是因为其没有运动部件,并且寿命长,振动小,结构简单,可靠性高。脉冲管制冷机的主要任务是将航天卫星上的红外探测器温度降到液氮温区附近,降低背景噪声,从而提高探测器的探测范围和灵敏程度。但由于脉冲管制冷机在空间应用和地面实验可能会存在重力的差异,导致脉冲管制冷机在应用阶段和实验阶段可能会存在一定的差异。重力影响的物理原理一般解释为开放脉管内的自由对流[1]。当脉冲管的热端不处于向上方向时,这种差异的影响水平大到足以阻止系统在地面测试时的运行要求[2]。有研究表明,重力对于小长径比的脉冲管制冷机影响更大[3],这里的长径比一般指脉冲管的长径比。所以,试图探寻重力的影响规律,对于指导小长径比脉冲管制冷机的地面实验有意义。

到目前为止,国内外也相继报道了重力特性研究的相关实验。2003 年,日本Masao Shiraishi 应用可视化技术,研究了长径比为20 的倾斜孔板脉管制冷机典型倾斜角为0—180°时的二次流动,发现重力驱动对流与声流的叠加很好地解释了流型与倾角的关系[1]。2009 年,美国新墨西哥州Los Alamos 国家实验室凝聚态物质和热物理组通过实验发现,重力驱动对流被声波振荡抑制的倒置脉冲管类似于倒摆,通过其枢轴点的高频振动来稳定[4]。2017 年,美国T Fang 等通过模拟和实验,结果表明,冷端组件的微小几何特征对脉管制冷机的重力定向灵敏度有很大的负面影响[5]。另外国内也进行了诸多探索。1998 年中国科学院低温技术实验中心杨鲁伟等通过对同轴型制冷机进行实验,发现重力在冷端向下时可以改善制冷性能,在冷端向上时降低制冷机性能[6]。2001年西安交通大学胡延东等通过计算和实验表明,冷端在下时,自然对流对脉冲管内的换热有抑制的作用,有利于保持两端的温差[7]。2002 年,西安交通大学何雅玲等对长径比为18.7 的脉冲管内的自然对流进行了模拟和实验测量。实验表明当冷端在下时获得的制冷温度最低;当热端在下并与重力方向成30°时制冷温度最高[8]。2008 年,中国科学院理化技术研究所侯小锋等通过数值模拟和实验研究指出,冷指方向与重力方向的夹角变化会对脉冲管制冷机的性能产生较大的影响,在135°时脉冲管内部会形成环流[9]。

但是,有研究发现,U 型脉冲管制冷机在温度超过65 K 时,各角度制冷量变化在3%以内,脉冲管倾角的影响不大[10]。另外,2002 年,在对流层发射光谱仪的地面测试中,对仪器的低温组件进行的第一次地面测试,没有观察到重力方向的影响。然而,在使用相同的脉冲管定向的仪器级测试中,发现了显著的方向性影响[11]。

由此看来,近10 多年来对于脉冲管制冷机重力特性研究较少,对于不同类型的脉冲管制冷机角度对脉冲管制冷机的制冷性能影响还没有定论,而且实验大多是针对长径比为20 左右的大长径比脉冲管制冷机。所以,对于脉冲管制冷机的重力特性的研究仍任重而道远。本研究针对实验室自主研制的长径比为4 的小长径比同轴脉冲管制冷机进行重力特性的实验研究,从而进一步探究脉冲管制冷机的重力特性。

2 实验研究

2.1 实验装置

本实验研究是在重力特性实验台上完成的。压缩机采用实验室研制的大功率对置线性压缩机,制冷机为同轴型脉冲管制冷机,采用惯性管加气库的调相方式,脉冲管长径比为4。实验装置主要包括温度采集、充气、真空、冷却、角度调节等部分。具体实物图和示意图如图1 所示。系统充气压力为3.5 MPa。实验通过不锈钢管连接冷指与线性压缩机,并在压缩机箍和压缩机座上设置通孔,相邻孔之间的间隔为15°,从而使得冷指可以绕压缩机旋转,改变冷指轴向与重力方向的夹角。实验中规定冷指中温度梯度的反方向与重力方向的夹角为角θ。

图1 重力特性实验实物图与示意图Fig.1 Physical diagram and schematic diagram of gravity characteristic experiment

2.2 制冷机性能

图2 是输入功率为150 W、200 W、300 W 时,脉冲管制冷机无负荷最低温度随重力方向的变化情况图。当温度发生波动难以稳定时,取波动时最高温度与最低温度的算术平均值。从图中可以看出,脉冲管制冷机无负荷最低温度与输入功率关联度较大。当输入功率为150 W 时,各角度无负荷最低温度温差最大达到30 K 以上,而在300 W 输入功率时,其差值不超过10 K。说明随着输入功率的增加,角度对于脉冲管制冷机的性能影响变小。这是由于不同角度下,脉冲管内的对流会影响制冷效果,有的文章中把这种影响称为对流寄生热负荷[10]。而输入功率越高,制冷机制冷量越大,越容易把这种对流寄生热负荷抵消掉。在同一输入功率下,倾角在60°以内制冷机的冷指温度随角度变化很小,温差在2 K 以内。在倾角大于60°时,冷指温度变化较大,随角度先增大后减小,最高温度出现在135°—150°附近,在此角度范围内,制冷机性能最差。当角度大于150°时,制冷机制冷性能又有所恢复。这是由于制冷机有将脉冲管内气体沿脉冲管轴向方向按温度分层的趋势,当角度为180°时,由于这时的对流方向也是沿脉冲管轴向方向的,制冷机的这种分层的趋势会把对流“抵消”;当角度大于90°小于180°时,脉冲管内的对流可以分解为沿轴向方向和沿径向方向两个部分,沿轴向方向的对流可以被这种趋势所抵消,而沿脉冲管径向的对流不能够被抵消,而此时的气体温度分层不垂直于脉冲管轴向方向,所以脉冲管内气流的掺混会更加严重。所以当脉冲管制冷机处于重力场工作时,应尽量使角度保持在0°,此时的性能最佳;一般情况下,尽量将角度控制在60°以内,否则会对制冷机性能产生较大影响。

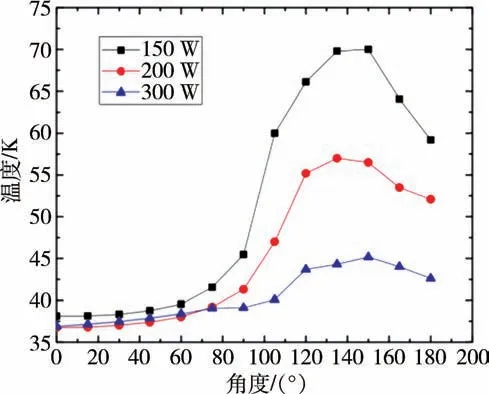
图2 不同输入功率无负荷最低温度随角度变化Fig.2 Variation of no-load minimum temperature with angle at different input power

为了探究角度对制冷量的影响,将相同输入功率下角度为0°时的80 K 温度下的制冷量定为标准制冷量,其余角度的80 K 制冷量相对于0°的比值看作相对制冷量。图3 采用极坐标图的形式展示了各输入功率下不同角度的相对制冷量。从图中可以看出,在150 W 输入时,135°—150°的相对制冷量最小,这也同时说明了此角度下制冷能力最差。在150 W 输入时,80 K 相对制冷量最低到0.2 左右;300 W 输入时,80 K 相对制冷量最小为0.9 左右,约为150 W 输入时的4.5 倍。所以输入功率越高,相对制冷量波动就越小,同一角度下相对制冷量数值越大。

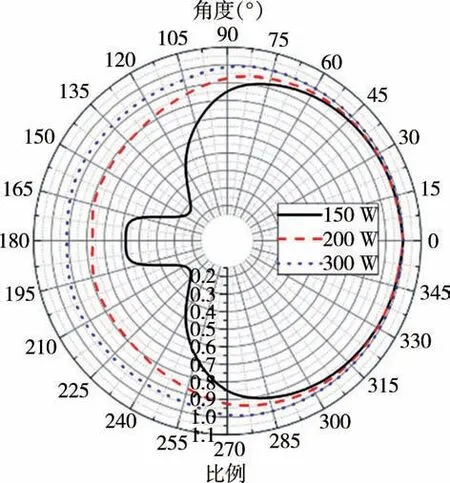
图3 不同输入功率下的相对制冷量Fig.3 Relative refrigerating capacity under different input power

图4 分别展示了150 W、200 W、300 W 制冷机的性能曲线。从图4a 可以看出,在夹角不大于90°时,制冷机的制冷曲线保持着较好的线性关系,当角度处于90°与180°之间时,制冷机的制冷曲线线性关系较弱。当角度为180°时,又恢复了不大于90°时的线性关系,并且其斜率要大于前者。并且在0°到135°,制冷机制冷性能不断变差,135°到180°,制冷机性能逐渐恢复至105°到120°之间的水平。从图4 可以看出,伴随着输入功率的增加,呈现非线性的性能曲线逐渐变少,这也同时印证了随着输入功率增加,角度对于脉冲管制冷机的性能影响变小这一现象。

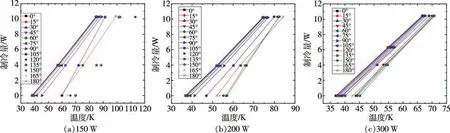
图4 不同输入功率下性能曲线Fig.4 Performance curve under different input power

2.3 温度、输入功率和电流的波动

当在某一固定角度实验时,温度在趋于稳定时会产生波动,导致无法维持在某一个确切数值。同时,输入功率与电流也有波动产生。通过观察发现,绝大多数测试实验能够在波动产生15 分钟后到达波动的稳定状态,所以实验中,取波动产生15 分钟后的波动值,作为本次实验的数据值,如图5d 所示。图5 所示是无负荷下不同输入功率下各角度温度、输入功率与电流波动值。其中,波动值的计算是产生波动时最大的数值与最小数值之差。从图中可以看出,温度、输入功率与电流的波动大小的变化趋势基本一致。当脉冲管内流场发生变化时,这种变化会直接作用于压缩机的输入功率,从而间接导致电压和电流的变化。当角θ大于90°时,在重力的作用下,温度高的介质会与温度低的介质发生掺混,导致脉冲管中介质的紊乱程度增加。在流场紊乱程度和输入功率的共同作用下,冷指冷端的温度会出现与二者相同趋势的变化。从图中可以看出,输入功率越高,相同角度下各参数的波动值越小。另外,同一输入功率下,各参数的波动最大值集中在105°—165°区间内,说明在此角度区间内,脉冲管内流场展现了相对较强的不稳定性。0°—90°区间内,各参数基本不发生波动,在此区间内脉冲管内流场较为稳定。

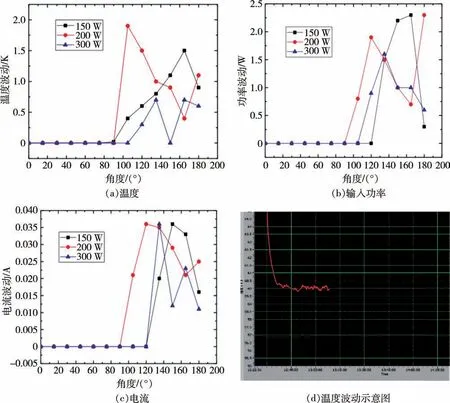
图5 不同参数随角度波动大小及温度波动示意图Fig.5 Schematic diagram of fluctuation of different parameters with angle and temperature

3 结论与分析

对小长径比脉冲管制冷机的重力特性进行了测试,通过实验研究,可以得出以下结论:

（1）制冷机在角度为135°—150°时制冷能力最差。在150 W 输入时,80 K 相对制冷量最低达到0.2左右。

（2）随着输入功率的增加,角度变化对于脉冲管制冷机的影响变小。300 W 输入时的最低相对制冷量约为150 W 输入时的4.5 倍左右。

（3）温度、输入功率与电流的波动大小的变化趋势变化基本一致。同一输入功率下,各参数的波动最大值集中在105°—165°区间内。

（4）输入功率越高,相同角度下各参数的波动值越小。