考虑客户满意度的城市冷链物流路径优化

文/唐聪 曾理宁 阳敏

近年来，随着城市冷链物流的快速发展，提高城市冷链物流配送质量，降低配送成本，使配送效益最大化已成为城市冷链物流中迫切想要实现的目标。论文综合考虑了冷链物流的特点，引入影响客户满意度的混合时间窗为主要约束条件，构造了以满足时间窗约束的最小成本为目标的函数模型，并且通过对应的遗传算法进行求解。结合冷链物流配送的实例数据，采用MATLAB编程求解出不同约束下的路径和各项成本费用，并进行对比分析。结果表明，考虑客户满意度的模型与算法能够有效降低成本和提高客户满意度。

1.引言

在冷链物流配送路径优化研究方面，国外学者就其中相关研究已经有了一系列的成果。Brito[2]等学者在考虑了冷链食品配送过程中的客户服务时间约束之后，建立了相关的优化路径模型，通过一个GRASP-VNS算法对模型求得最优解，找出了最优路径；F.Errico等学者[3]以两个阶段随机规划模型为基础，将带有硬时间窗和随机服务时间的配送车辆问题限定为集合规划问题，然后求解；许敏[4]在研究带时间窗的生鲜冷链物流时，对遗传算法的各个部分进行了细致的改进以完成其模型的优化，得到了一条优化路径，并依据这些结果对生鲜食品企业在配送过程中提出了一系列有效的优化对策建议；姚宝珍等[5]研究了带时间窗的西餐连锁店配送路径优化问题（VRPTW）,在运用了启发式算法对VRPTW问题进行求解最优路径时，还引入了一种自适应转移策略来提高算法的求解效率，并且通过大量实例验证了算法的可行性；吴欣[6]针对生鲜产品冷链物流配送时间和总成本最小化为目标，在考虑实时拥堵指数和配送时间窗的约束下，构建成本最小化模型，并结合行驶过程中三个连续阶段的拥堵指数导致的行驶时间变化,从而得到优化策略，最后，使用模拟退火算法对多目标模型进行求解，通过实际案例验证了模型的实用性和算法的有效性；施文嘉等[7]学者构建了冷链物流最小配送总成本数学模型，充分考虑生鲜食品本身具有的易腐性特质及其在配送过程中必要的能源成本和货损成本，加入软时间窗的限制及车辆载荷等约束条件，采用免疫优化算法，确定了最优路径方案；

本文研究的是城市区域冷链物流配送中的VRP问题，即对冷链物流的配送路径进行优化，考虑了距离、载重量、客户满意度等影响因素后，在尽可能满足客户要求的时间窗的基础上使配送路径最短，从而达到提高客户满意度，降低配送成本的目的。

2.城市冷链物流配送路径模型

2.1 问题描述与模型假设

论文关注模糊时间窗下的冷链物流配送路径问题。在城市的某个区域中，一个配送中心为若干客户需求点进行冷链物流配送服务，配送中心和每个需求点的具体位置坐标是已知的，但是各客户的需求量和要求送货时间有所不同，要求配送中心安排冷链配送车辆运输时的路径使得尽可能在客户要求的时间内到达且总配送成本最低。

在构建模型时，假设唯一配送中心0有足够的M辆冷藏车满足一次性完成此次配送，单车最大载重量为Q吨，需要给N个需求点进行配送，配送中心和每个需求点的具体位置坐标、送达时间和需求量已知，所有车辆均由配送中心出发，全程在保持商品所需储藏温度基础上匀速行驶，速度为V，在满足所有需求点后，最终返回配送中心。

2.2 成本模型

根据对冷链物流的问题描述和模型假设可以建立以配送总成本最小为目标的函数模型，其中，配送总成本包括固定成本、运输成本和时间惩罚成本。

涉及各项成本的相关参数规定如表2-1所示。

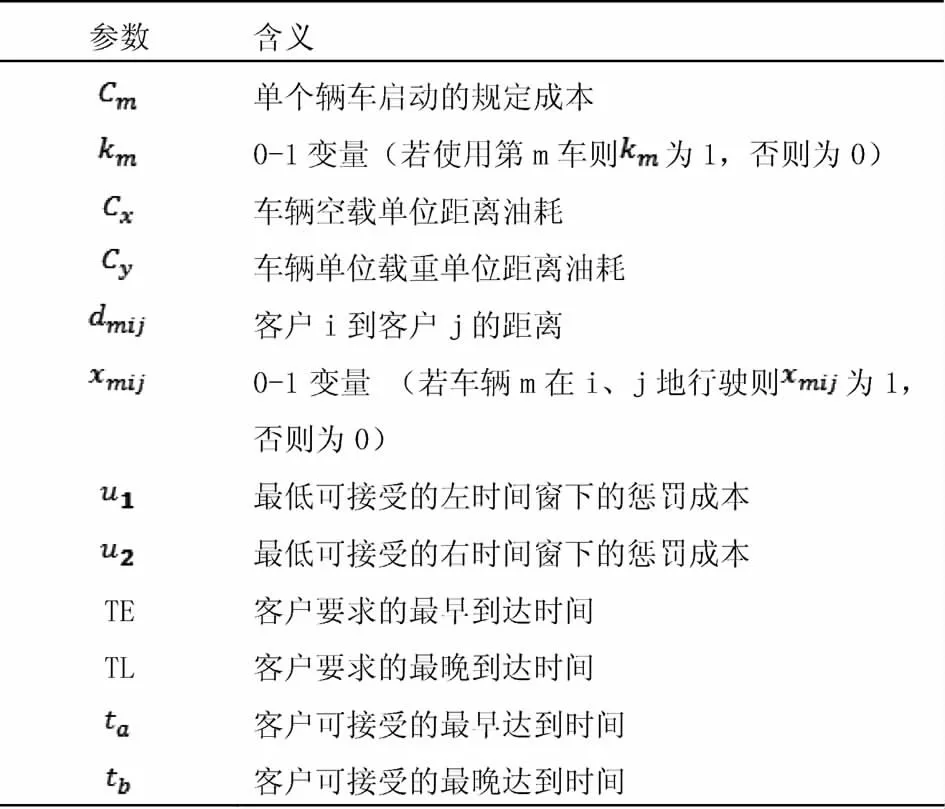
表2 -1参数含义表

2.2.1 固定成本

在城市冷链物流中，配送中心为实现某一配送目标，需要启动一定数量的汽车完成配送，就会产生一个固定成本，这个成本包括车辆启动成本、驾驶员工资、折旧损耗等，则该固定成本C1为：

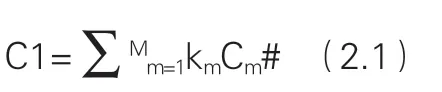
2.2.2 运输成本

城市冷链物流中的运输成本是随配送路径的选择和载重的变化而变化，通常只与车辆的运输距离和车辆载重有关，因此运输成本C2为：

2.2.3 时间惩罚成本

时间惩罚成本是整个物流系统中较为关注的地方，在模糊时间窗中，如不能在需求点最期望的时间范围内送达，就会有一些惩罚，但只要在需求点可容忍的时间范围内送达，则只需支付相应的惩罚成本，当然，若超出可容忍的接受时间范围，则需求方拒收，或认为惩罚成本无限大。

因此，在分析时间惩罚成本是可以将其视为硬时间窗和软时间窗下的多条件成本。如式2.3所示，可将配送车辆到达时间分为四种情况。若在TE和TL时间段内运输到达，则认为符合客户要求的送达时间，此时时间惩罚成本为0；若配送车辆在至TE之间或TL至之间到达，则认为此次配送不在客户要求的时间内，但客户仍能接受缴纳违约金的此次配送，且还能维持和客户的供需关系，并假设其违约金与迟到和早来的时间呈一定的线性关系；若配送车辆在之前或之后送达，则认为此次配送完全不符合客户要求，配送不可行。所以，对于任何一个送达的时间时间惩罚成本C3为：

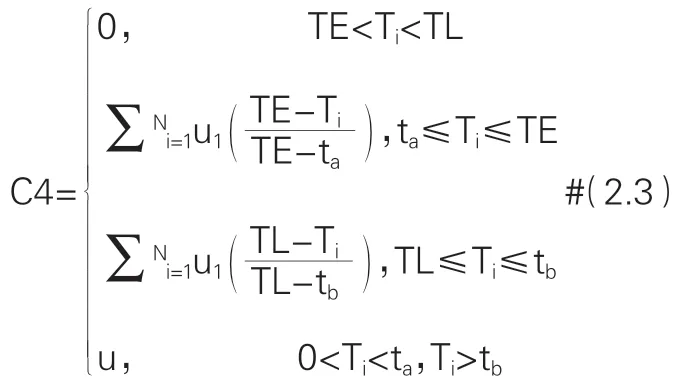
2.2.4 总成本

综上所述，考虑客户满意度的城市冷链物流总成本为：

式（2.4）表示最小配送成本；

式（2.5）表示确保每一辆车配送时最大载货量不超过其最大容量；

式（2.6）和式（2.7）表示每个客户都只会被一辆车服务到，且每个客户都只是被服务一次；

式（2.8）表示为客户服务的车辆数量最多不超过配送中心已有车辆；

式（2.9）表示每辆为客户服务的车辆从配送中心出发，并最终返回配送中心；

式（2.10）和（2.11）表示0-1变量的定义。

3.算例分析

3.1 算例描述及参数设定

论文是以长沙某一的配送中心为其客户的配送过程为实例，以配送中心周围12个客户作为配送点，将配送中心编号为0，12个配送点分别编号为1、2、3、……、12。各参数的设定如表4-1所示：

另外，客户可容忍的接受货物的时间在客户要求的送达时间窗的前后半个小时（例：要求时间为7：00-8：00，即客户最长可接收货物的时间为6：30-8：30）；而且，在此次模拟分析中不考虑因车辆运输途中遇见特殊事故导致配送失败产生的其它成本。

如表3-1和表3-2所示，已知12个客户的坐标及其相互之间的最短距离、各客户的需求量、时间窗要求、服务时间。论文将设冷链车辆的载重为5t，并假设配送过程中车辆匀速行驶，以各点之间的最短路径为行驶路径，不考虑交通拥堵和其它情况，行驶速度为20km/h。

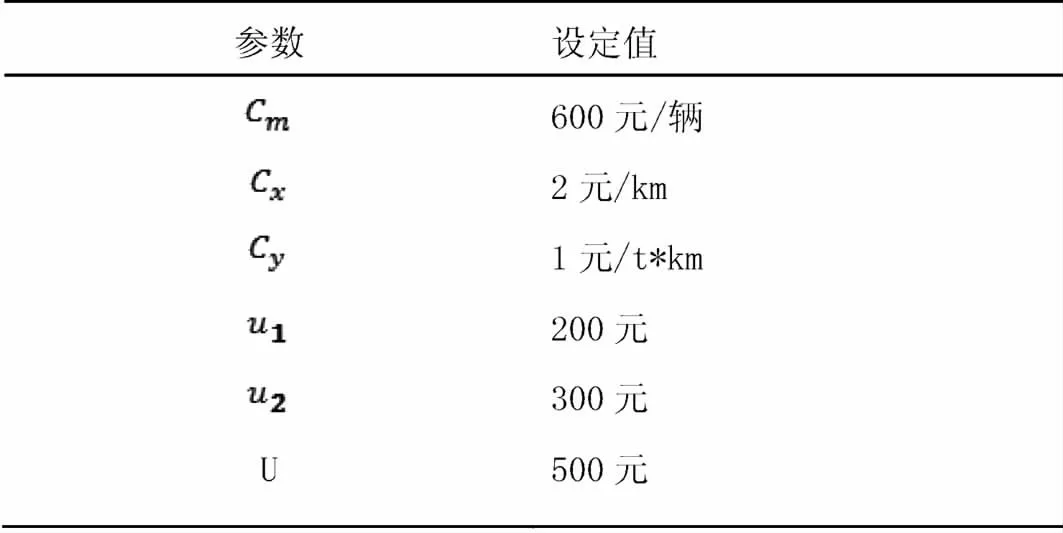
表3 -1参数设定表

3.2 运算结果

论文使用MATLAB R2014b编程软件求解，以满足客户时间窗为目标，代入客户坐标、需求量等信息，并假设所使用的遗传算法中的交叉概率为0.9，变异概率为0.05，在迭代200代后的结果后，得到了考虑客户满意度时和考虑距离时各最优路径如3-4所示，其各项成本及客户满意度、总距离如表3-4所示。

表3 -2配送中心与12客户的最短配送距离（单位/百米）

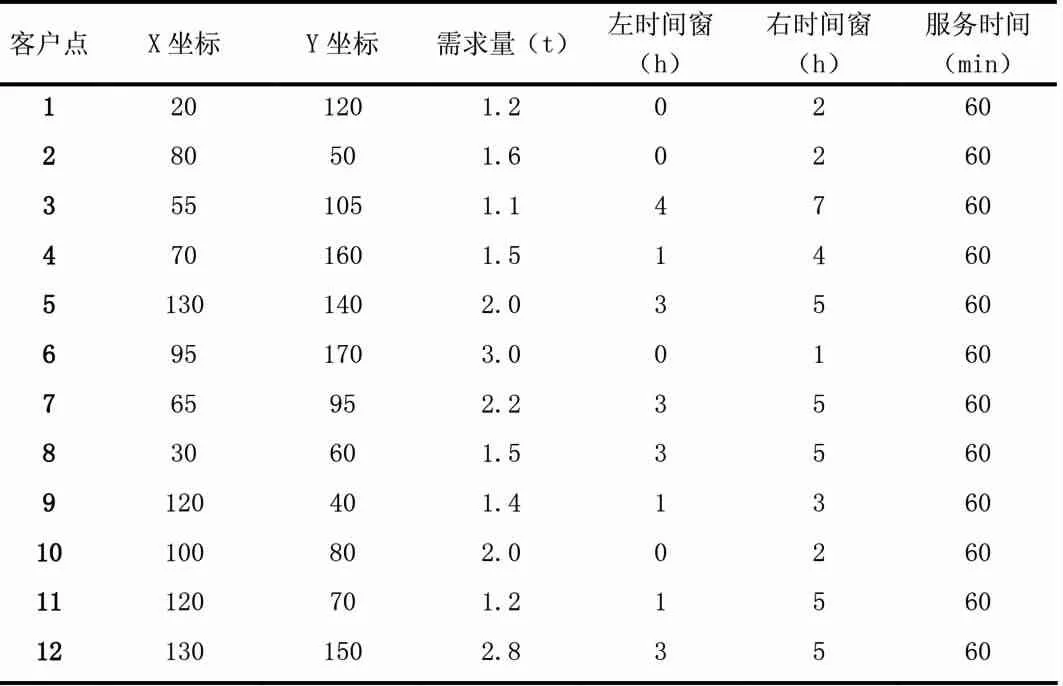
表3 -3各客户的相关信息

表3 -4最优路径表

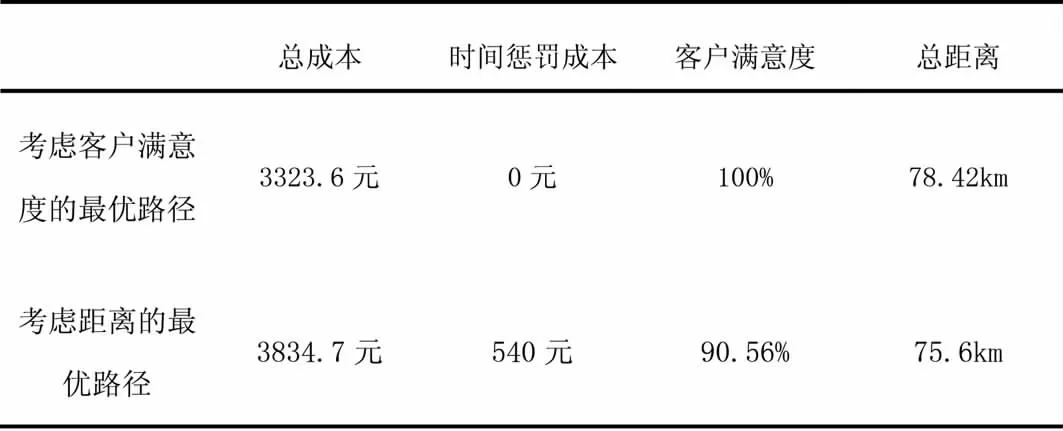
表3 -5有无考虑客户满意度的对比关系表

3.3 结果分析

从表3-4的对比关系来看，考虑客户满意度后，配送总成本得到了一定程度的降低，仅为3323.6元，相比与未考虑客户满意度时的总配送成本3834.7元，降低了13.33%；对于时间惩罚成本而言，由于考虑客户满意度的配送不存在违背客户要求的时间窗的情况，因此无时间惩罚成本，客户满意度也为100%，而在没有考虑客户满意度的情况下，有严重的违背客户的规定的时间窗要求，因此产生了较大的时间惩罚成本，为540元，且客户满意度仅为90.56%；但在没有考虑客户满意度的情况下，是以距离最小为最优的一种配送，所以其总距离是教小的，为75.6km，因此在考虑客户满意度后的配送距离78.42km,相比于之前的配送距离增加了3.73%。

从全方位来看，考虑了客户满意度的配送是比没有考虑时更好的，在成本方面有了明显的优化，客户满意度100%，在这种情况下，既能降低企业配送成本，又能维持和客户的长久合作的关系，反观在没有考虑客户满意度的情况下，则难以达成这个目标。

4.结语

在当代社会的经济活动中，物流企业的降本增效是一条必经之路，另外，物流企业也将更加注重以客户为中心实现业务运转。在本文中，构造了以客户满意度为目标的成本模型和没有考虑客户满意度，仅以距离最小为目标的成本模型，并使用MATLAB编程，运用遗传算法得到了两种情况的最优路径和相关成本，通过对比可知，在考虑了客户满意度的情况下，总成本明显更低，而且客户满意度更高，这种结果在一定程度上满足了企业在降低成本的同时提高服务水平的要求，使得企业在未来竞争中更具有优势，符合绿色物流、经济物流的发展要求。C